文档内容
秘密★启用前【考试时间 5月14日15:00—17:00】
射洪市 2024 年普通高考模拟测试
数 学
(理工农医类)
满分150分。考试时间120分钟。考生作答时,须将答案答在答题卡上,在本试题卷
或草稿纸上答题无效。考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共 60 分)
注意事项:必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。
一、选择题: 本大题共12小题,每小题5分,共60分.在每小题给出的四
个选项中,只有一个是符合题目要求的.
1.已知集合 , ,则
A. B. C. D.
DCC D
2.复数 ( 是虚数单位)在复平面内对应的点位于
1 1
Q
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.某学校为了解1 000名新生的身体素质,将这些学生编号为 1,2,…,1
000,从这些新生中用系统抽样方法等距抽取 100名学生进行体质测验.若46
号学生被抽到,则下面4名学生中被抽到的是
A.815号学生 B.616号学生 C.200号学生 D.8号学生
A BPQ
4.已知 ,则
1
√6 ΔA BQ
A. B. C. D.
1
5.设 是两条不同的直线, 是三个不同的平面,下列说法中正确的序号
为
①若 ,则 为异面直线 ②若 ,则
③若 ,则 ④若 ,则
A.①② B.②③ C.③④ D.②④
6.在 中,点F为线段BC上任一点(不含端点),若
,则 的最小值为
A.3 B.4 C.8 D.9
7.下列函数满足 的是
A. f(x)=1+lnx B.C. D.
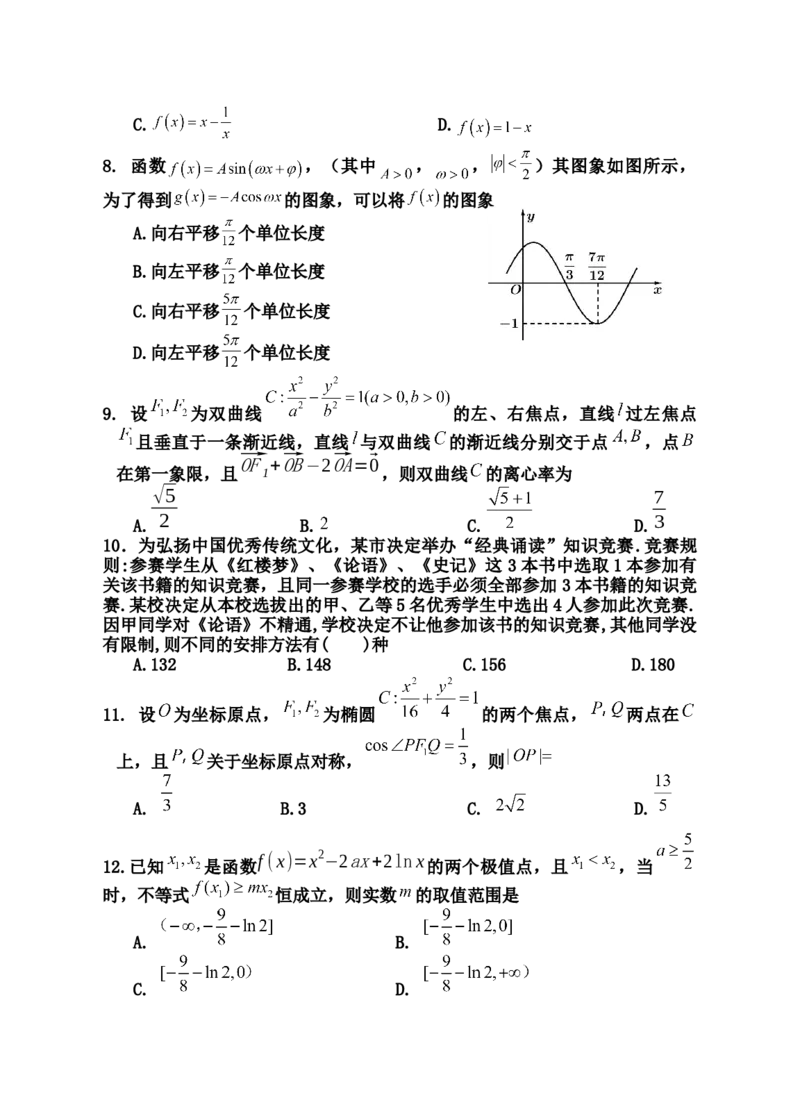
8. 函数 ,(其中 , , )其图象如图所示,
为了得到 的图象,可以将 的图象
A.向右平移 个单位长度
B.向左平移 个单位长度
C.向右平移 个单位长度
D.向左平移 个单位长度
9. 设 为双曲线 的左、右焦点,直线 过左焦点
且垂直于一条渐近线,直线 与双曲线 的渐近线分别交于点 ,点
⃗OF +O⃗B−2O⃗A=0⃗
在第一象限,且 1 ,则双曲线 的离心率为
√5 7
A. 2 B. C. D.3
10.为弘扬中国优秀传统文化,某市决定举办“经典诵读”知识竞赛.竞赛规
则:参赛学生从《红楼梦》、《论语》、《史记》这 3本书中选取1本参加有
关该书籍的知识竞赛,且同一参赛学校的选手必须全部参加 3本书籍的知识竞
赛.某校决定从本校选拔出的甲、乙等5名优秀学生中选出4人参加此次竞赛.
因甲同学对《论语》不精通,学校决定不让他参加该书的知识竞赛,其他同学没
有限制,则不同的安排方法有( )种
A.132 B.148 C.156 D.180
11. 设 为坐标原点, 为椭圆 的两个焦点, 两点在
上,且 关于坐标原点对称, ,则
A. B.3 C. D.
12.已知 是函数
f(x)=x2 −2ax+2lnx
的两个极值点,且 ,当
时,不等式 恒成立,则实数 的取值范围是
A. B.
C. D.第Ⅱ 卷(非选择题 共 90 分)
二、填空题: 本大题共4小题,每小题5分,共20分.
13. 若 满足约束条件 ,设 的最大值为 ▲ .
x2 y2 4x0 x2 y2 4y 0
14.已知两圆的方程分别为 和 ,则这两圆公共弦
的长等于 ▲ .
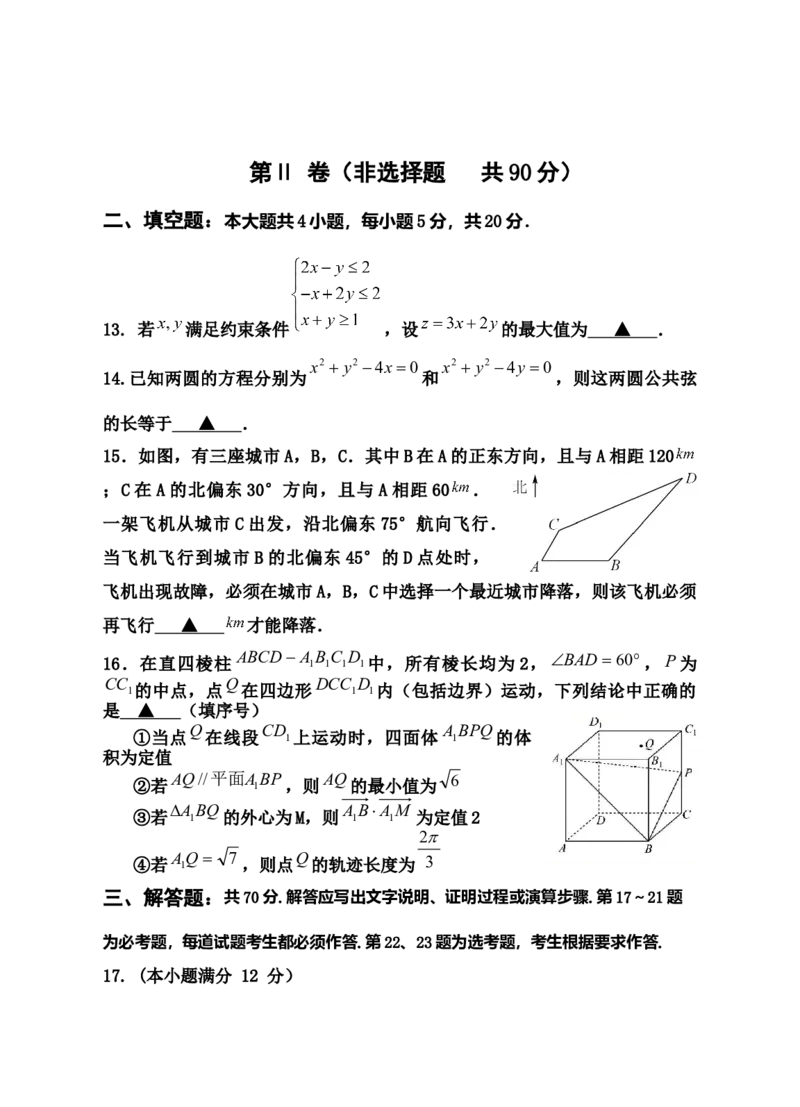
15.如图,有三座城市A,B,C.其中B在A的正东方向,且与A相距120
;C 在 A 的北偏东 30°方向,且与 A 相距 60 .
一架飞机从城市 C 出发,沿北偏东 75°航向飞行.
当飞机飞行到城市 B 的北偏东 45°的 D 点处时,
飞机出现故障,必须在城市A,B,C中选择一个最近城市降落,则该飞机必须
再飞行 ▲ 才能降落.
16.在直四棱柱 ABCD A 1 B 1 C 1 D 1中,所有棱长均为 2,BAD 60,P为
CC Q DCC D
1的中点,点 在四边形 1 1内(包括边界)运动,下列结论中正确的
是 ▲ (填序号)
Q CD A BPQ
①当点 在线段 1上运动时,四面体 1 的体
积为定值
AQ//平面A BP AQ 6
②若 1 ,则 的最小值为
A BQ A BAM
③若 1 的外心为M,则 1 1 为定值2
2
④若 A 1 Q 7 ,则点 Q 的轨迹长度为 3
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题
为必考题,每道试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
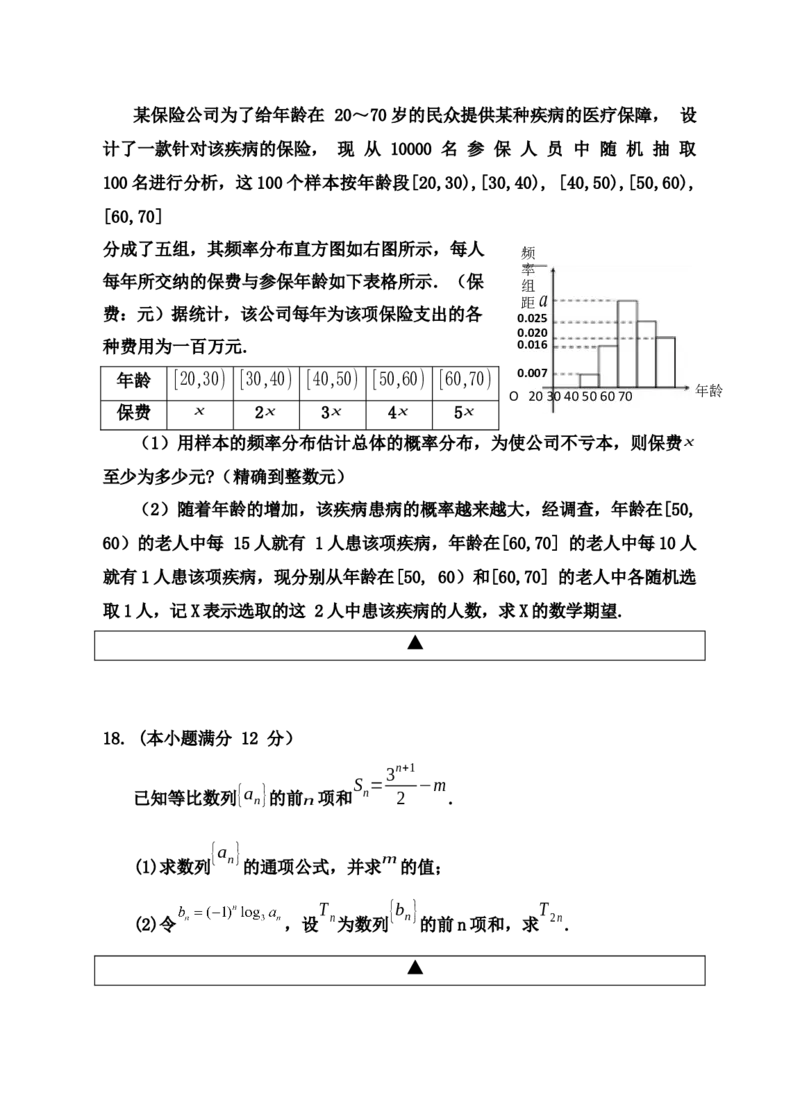
17. (本小题满分 12 分)某保险公司为了给年龄在 20~70岁的民众提供某种疾病的医疗保障, 设
计了一款针对该疾病的保险, 现 从 10000 名 参 保 人 员 中 随 机 抽 取
100名进行分析,这100个样本按年龄段[20,30),[30,40), [40,50),[50,60),
[60,70]
分成了五组,其频率分布直方图如右图所示,每人
频
率
每年所交纳的保费与参保年龄如下表格所示.(保
组
a
距
费:元)据统计,该公司每年为该项保险支出的各
0.025
0.020
种费用为一百万元. 0.016
年龄 [20,30) [30,40) [40,50) [50,60) [60,70) 0.007
年龄
O 20 30 40 50 60 70
保费 x 2x 3x 4x 5x
(1)用样本的频率分布估计总体的概率分布,为使公司不亏本,则保费x
至少为多少元?(精确到整数元)
(2)随着年龄的增加,该疾病患病的概率越来越大,经调查,年龄在[50,
60)的老人中每 15人就有 1人患该项疾病,年龄在[60,70] 的老人中每10人
就有1人患该项疾病,现分别从年龄在[50, 60)和[60,70] 的老人中各随机选
取1人,记X表示选取的这 2人中患该疾病的人数,求X的数学期望.
▲
18. (本小题满分 12 分)
3n+1
S = −m
已知等比数列{a }的前 项和 n 2 .
n n
{a }
n m
(1)求数列 的通项公式,并求 的值;
T {b } T
n n 2n
(2)令 ,设 为数列 的前n项和,求 .
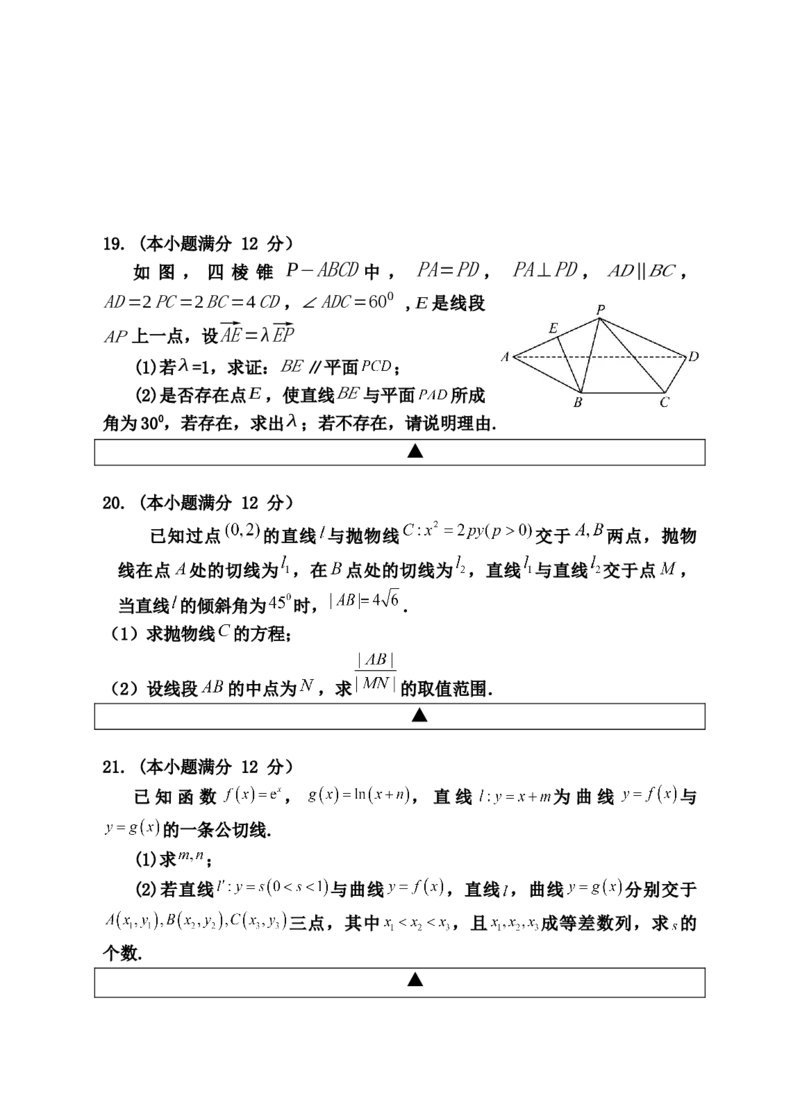
▲19. (本小题满分 12 分)
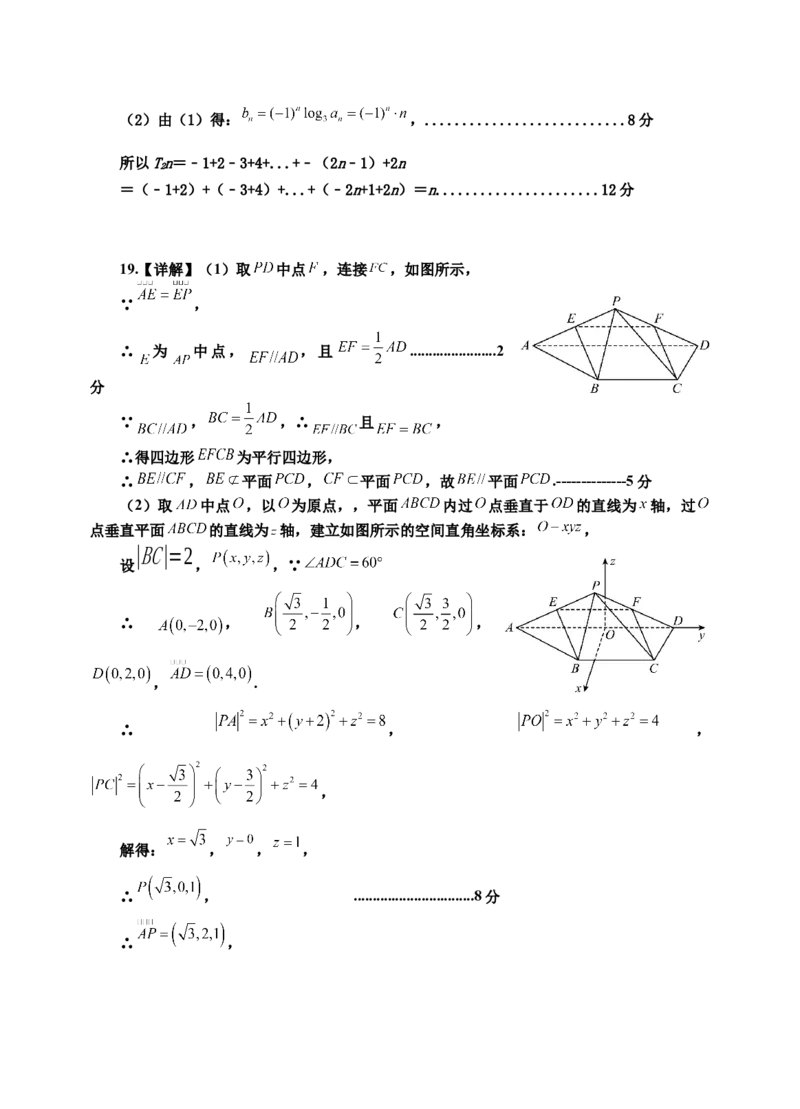
如 图 , 四 棱 锥 P−ABCD 中 , PA=PD , PA⊥PD , AD∥BC,
AD=2PC=2BC=4CD,∠ADC=600 ,E是线段
AP上一点,设⃗AE=λ⃗EP
(1)若λ=1,求证:BE∥平面 ;
(2)是否存在点E,使直线BE与平面 所成
角为300,若存在,求出λ;若不存在,请说明理由.
▲
20. (本小题满分 12 分)
已知过点 的直线 与抛物线 交于 两点,抛物
线在点 处的切线为 ,在 点处的切线为 ,直线 与直线 交于点 ,
当直线 的倾斜角为 时, .
(1)求抛物线 的方程;
(2)设线段 的中点为 ,求 的取值范围.
▲
21. (本小题满分 12 分)
已 知 函 数 , , 直 线 为 曲 线 与
的一条公切线.
(1)求 ;
(2)若直线 与曲线 ,直线 ,曲线 分别交于
三点,其中 ,且 成等差数列,求 的
个数.
▲请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计
分.
【选修 4—4:坐标系与参数方程】(10 分)
C
M O
22.如图,在极坐标系中,已知点 (2,0),曲线 1是以极点 为圆心,以
( π)
2,
OM为半径的半圆,曲线C 是过极点且与曲线C 相切于点 2 的圆.
2 1
C C
(1)分别写出曲线 1, 2的极坐标方程;
θ=α(0<α<π,ρ∈R) C C A B
(2)直线 与曲线 1, 2分别相交于点 , (异
于极点),求△ABM面积的最大值.
x
▲
【选修 4—5:不等式选讲】(10 分)
f(x)=|x−1|
23.已知函数 .
(Ⅰ)求不等式 的解集;(Ⅱ)若函数 的最小值为 ,正数 , 满足 ,
证明: .
▲射洪市 2024 年普通高考模拟测试
理数参考答案及评分意见
一、选择题:本大题共12小题,每小题5分,共60分.
1-5:DABDB 6-10:DCCBA 11-12:CA
二、填空题:本大题共4小题,每小题5分,共20分.
10 60√6
13. 14. 15. 16.①④
三、解答题
18.【详解】(1)等比数列{an}的前n项和Sn= ﹣m ①.
当n=1时,解得 ,
当n≥2时, ②,
①﹣②得: ,
又{an}是等比数列,n=1时也符合,...............................4分
当n=1时, ,故m= .....................................6分(2)由(1)得: ,...........................8分
所以Tn=﹣1+2﹣3+4+...+﹣(2n﹣1)+2n
2
=(﹣1+2)+(﹣3+4)+...+(﹣2n+1+2n)=n......................12分
19.【详解】(1)取 中点 ,连接 ,如图所示,
∵ ,
∴ 为 中点, ,且 .......................2
分
∵ , ,∴ 且 ,
∴得四边形 为平行四边形,
∴ , 平面 , 平面 ,故 平面 .--------------5分
(2)取 中点 ,以 为原点,,平面 内过 点垂直于 的直线为 轴,过
点垂直平面 的直线为 轴,建立如图所示的空间直角坐标系: ,
|BC|=2
设 , ,∵
∴ , , ,
, .
∴ , ,
,
解得: , , ,
∴ , ................................8分
∴ ,设 , ,又
∴ ,设平面 的法向量为
∴ ,令 ,解得 , ,
∴ , ................................10分
∴ ,
整理得: ,解得 或 , ,
所以 ,解得 或 .................................12分
故存在点E使BE与平面PAD所成角为300
20. 【解析】(1)当 的斜率为 时,则 ,不妨设 ,
由 可 得 , , 所 以 ,
.............................3分
即
,因为 ,解得: .
从而抛物线 的方程为 .............................
5分
(2)设直线 , ,
由 可得, ,则所以 ,
于是
即 ··················7分
4√ (1+k2 )(k2 +2)
而
·······8分
由 ,则 ,
于是抛物线 在点 处的切线 的方程为
即
同理可得,在点 处的切线 的方程为
联立,解得 于是 ...............................10分
则
4√ (1+k2 )(k2 +2)
从而
所以, 的取值范围是 ...............................12分
21、【详解】(1)设 与 相切于点 ,, ,解得: ,
,即切点为 ,
,即 ; ...............................2分
设 与 相切于点 ,
, ,
即 ,
切线方程为: , ,
解得: , . ................................5分
(2)由题意得: ,则 , , ;
成等差数列,
,即 ,
; ...............................7分
令 ,则 ;
令 ,则 ,
在 上单调递增, , ,
,使得 ,即 ;
则当 时, ;当 时, ;
在 上单调递减,在 上单调递增;..............................9分.,
, ,则 ,即 ,
在 上单调递增,
, ,
在 上存在唯一零点,即 的个数为 ................................12分
22.解析;(1)由题意可知,曲线C 是以极点O为圆心,2为半径的半圆,
1
结合图形可知,曲线C 的极坐标方程为ρ=2(0≤C≤π).
1
π
−θ
设P(ρ, θ)为曲线C 上任意一点,则ρ=2cos(2 )=2sinθ,
2
ρ θ
∴曲线 C 的极坐标方程为 =2sin .(4分)
₂
ρ ρ ρ ρ ρ ρ
(2)设 A( A, a ),B( B, a ),由题意得 B=2sina· A=2,∴|AB|=| A- B|=2-2sina.
∵点M到直线AB的距离为d=|OM| sina=2sina,
1 1 (sina+1−sina) 2 1
|AB| =
∴S =2 ·d=2 (2-2sina)·2sina=2sina(1-sina)≤2× 4 2 ,
△ABM
1 1
当且仅当 sina=2 时,等号成立,故△ABM面积的最大值2 .(10分)