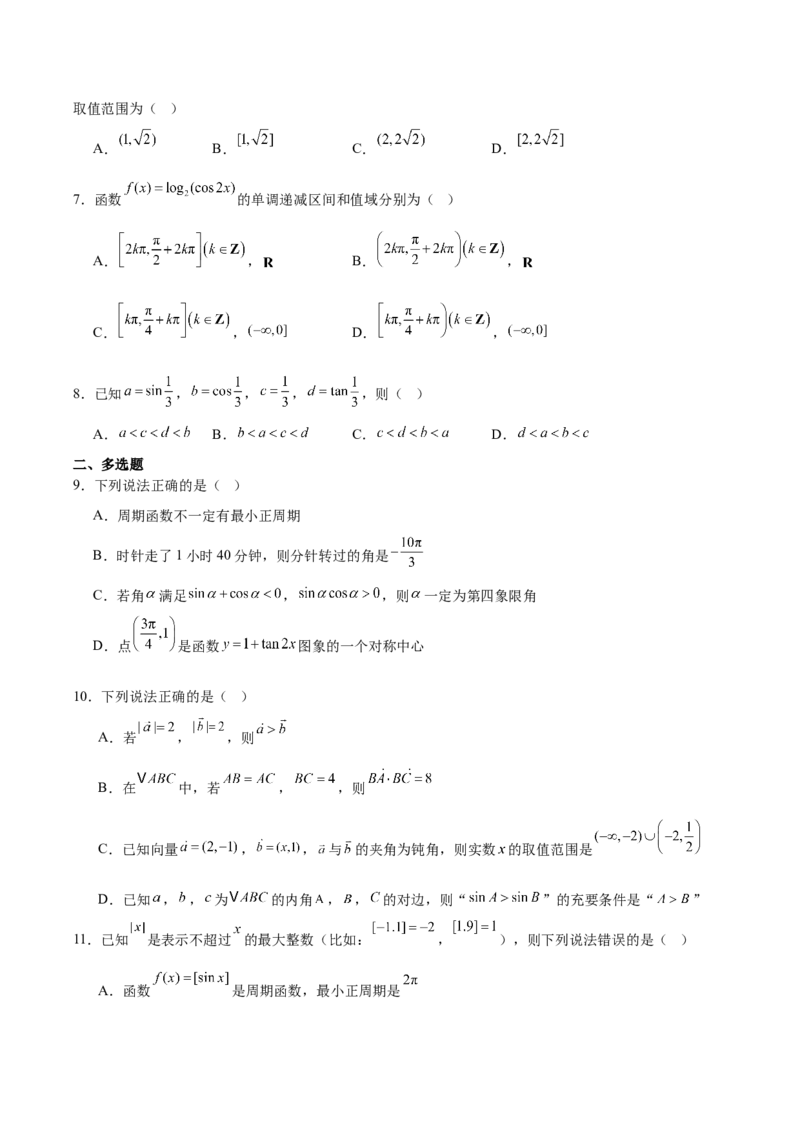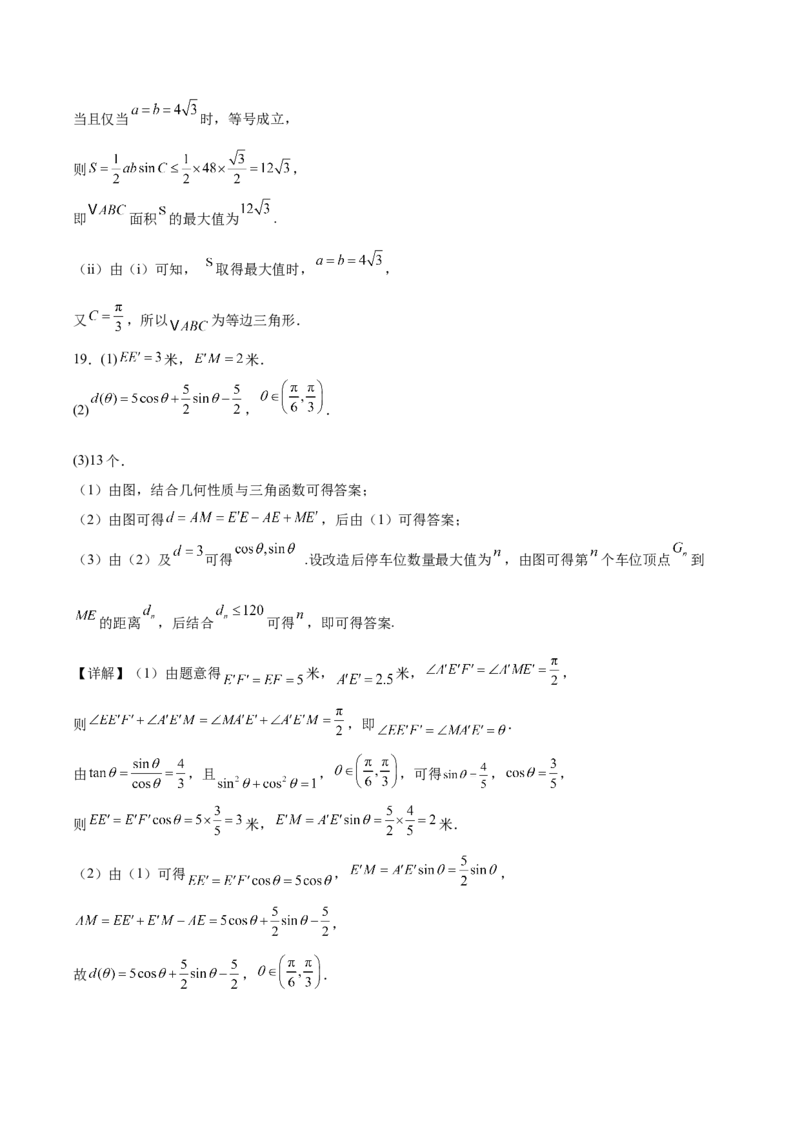文档内容
2024-2025学年高一下学期期中模拟联考
数学试题
一、单选题
1.计算 的结果为( )
A. B. C. D.
2.已知在 中, 且 ,则 的值为( )
A. B. C.2 D.3
3.以下变换中,能将函数 的图象变为函数 的图象的是( )
A.每个点的横坐标缩短为原来的 ,再向左平移 个单位长度
B.每个点的横坐标伸长为原来的2倍,再向左平移 个单位长度
C.向右平移 个单位长度,再将每个点的横坐标缩短为原来的
D.向右平移 个单位长度,再将每个点的横坐标伸长为原来的2倍
4.已知向量 , ,则向量 在 上的投影向量的坐标为( )
A. B. C. D.
5.已知函数① ,② ,③ ,④ ,⑤ ,则下列选项中同时满
足(1)是偶函数,(2)最小正周期是 ,(3)对称轴相同这三个条件的是( )
A.①②⑤ B.①③④ C.②③⑤ D.③④⑤
6.在 中, , , 分别是角 , , 的对边,已知 , 且 有两解,则实数 的取值范围为( )
A. B. C. D.
7.函数 的单调递减区间和值域分别为( )
A. , B. ,
C. , D. ,
8.已知 , , , ,则( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.周期函数不一定有最小正周期
B.时针走了1小时40分钟,则分针转过的角是
C.若角 满足 , ,则 一定为第四象限角
D.点 是函数 图象的一个对称中心
10.下列说法正确的是( )
A.若 , ,则
B.在 中,若 , ,则
C.已知向量 , , 与 的夹角为钝角,则实数 的取值范围是
D.已知 , , 为 的内角 , , 的对边,则“ ”的充要条件是“ ”
11.已知 是表示不超过 的最大整数(比如: , ),则下列说法错误的是( )
A.函数 是周期函数,最小正周期是B.函数 是周期函数,最小正周期是
C.若函数 ,则 的值域是
D.当 时,函数 的零点有5个
三、填空题
12.已知单位向量 , 的夹角为 ,则向量 , 的夹角为 .
13.已知关于 的方程 在 上有解,则实数 的取值范围为 .
14.如图,在梯形 中, , , 是 边所在直线上的动点,若该梯形的面积为
,则 的最小值为 .
四、解答题
15.(1)已知向量 , ,若 ,求实数 的值;
(2)已知向量 , , ,若 ,求 的值.
16.已知某扇形的周长是8.
(1)当该扇形的面积最大时,求其圆心角 的大小;
(2)在(1)的条件下,求该扇形中所含弓形的面积.(注:弓形是指在圆中由弦及其所对的弧组成的图
形.)
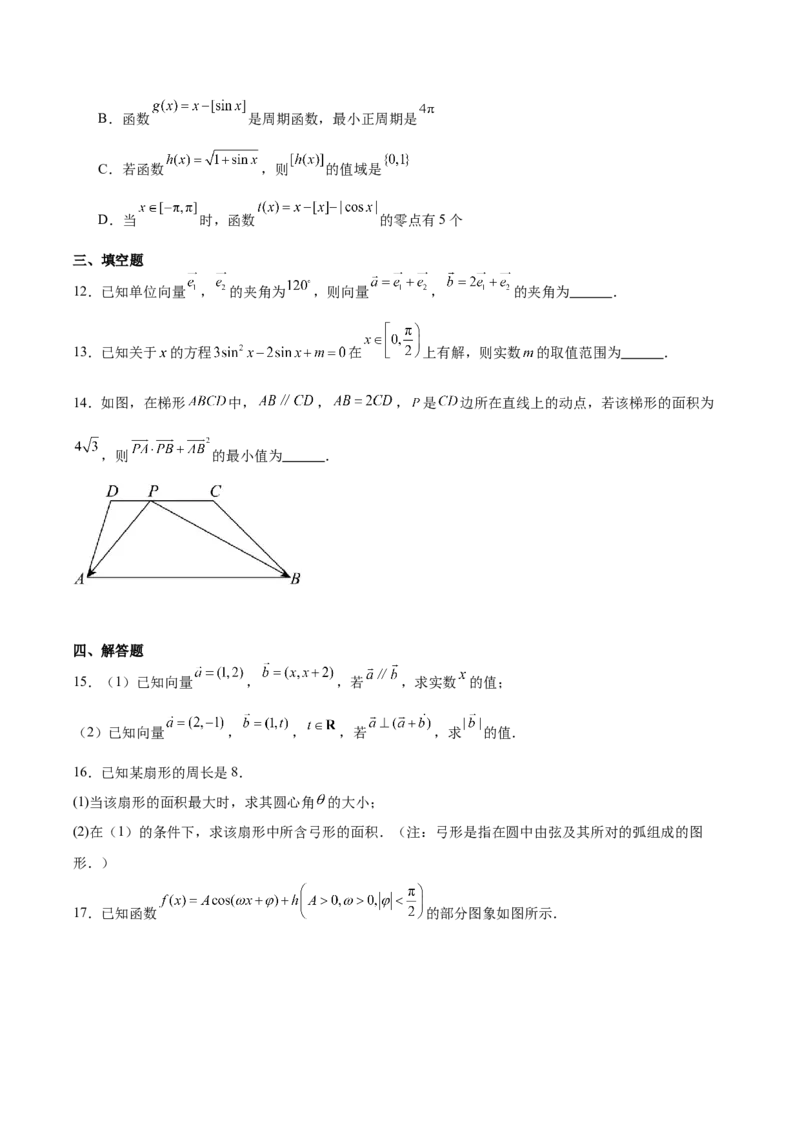
17.已知函数 的部分图象如图所示.(1)求 的解析式;
(2)将 的图象先向左平移 个单位长度,再将所有点的横坐标变成原来的 ,纵坐标保持不变,得到
函数 的图象,求 的单调递减区间和其图象的对称中心.
18.在 中, , , 分别是角 , , 的对边,已知 是锐角,向量 ,
,且 .
(1)若 ,求实数 的值.
(2)已知 .
(i)求 面积 的最大值;
(ii)在(i)的条件下,判断 的形状.
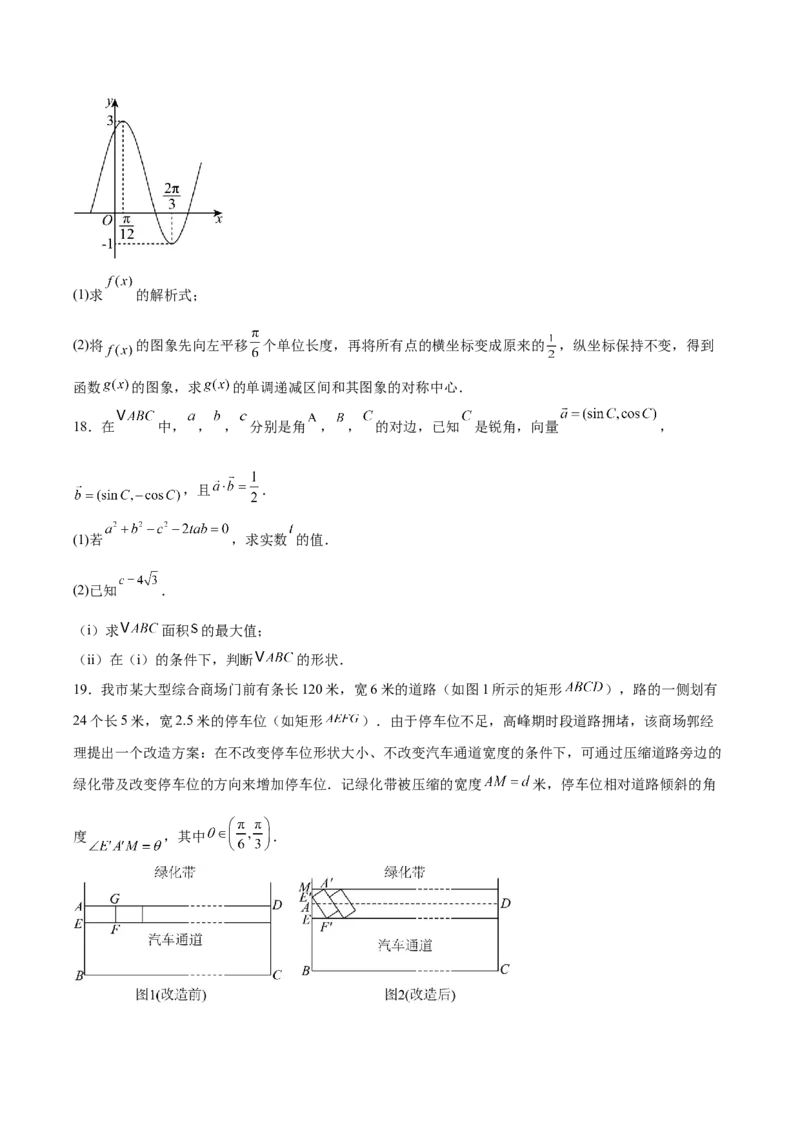
19.我市某大型综合商场门前有条长120米,宽6米的道路(如图1所示的矩形 ),路的一侧划有
24个长5米,宽2.5米的停车位(如矩形 ).由于停车位不足,高峰期时段道路拥堵,该商场郭经
理提出一个改造方案:在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边的
绿化带及改变停车位的方向来增加停车位.记绿化带被压缩的宽度 米,停车位相对道路倾斜的角
度 ,其中 .(1)若 ,求 和 的长;
(2)求 关于 的函数表达式 ;
(3)若 ,按照郭经理的方案,该路段改造后的停车位比改造前增加了多少个?题号 1 2 3 4 5 6 7 8 9 10
答案 A D B B B C D A ABD BCD
题号 11
答案 BD
1.A
利用诱导公式及特殊角的三角函数值求得答案.
【详解】 .
故选:A
2.D
将条件转化为 ,再利用平面向量基本定理即可.
【详解】因 ,则 ,
故 ,
则 ,所以 .
故选:D
3.B
由三角函数伸缩变换,平移变换知识结合诱导公式,可判断选项正误.
【详解】对于A,变换后的函数为
,故A错误;
对于B,变换后的函数为,故B正确;
对于C,变换后的函数为
,故C错误;
对于D,变换后的函数为
,故D错误.
故选:B
4.B
根据题意可得 ,进而求投影向量.
【详解】因为向量 , ,则 ,
所求投影向量的坐标为 .
故选:B.
5.B
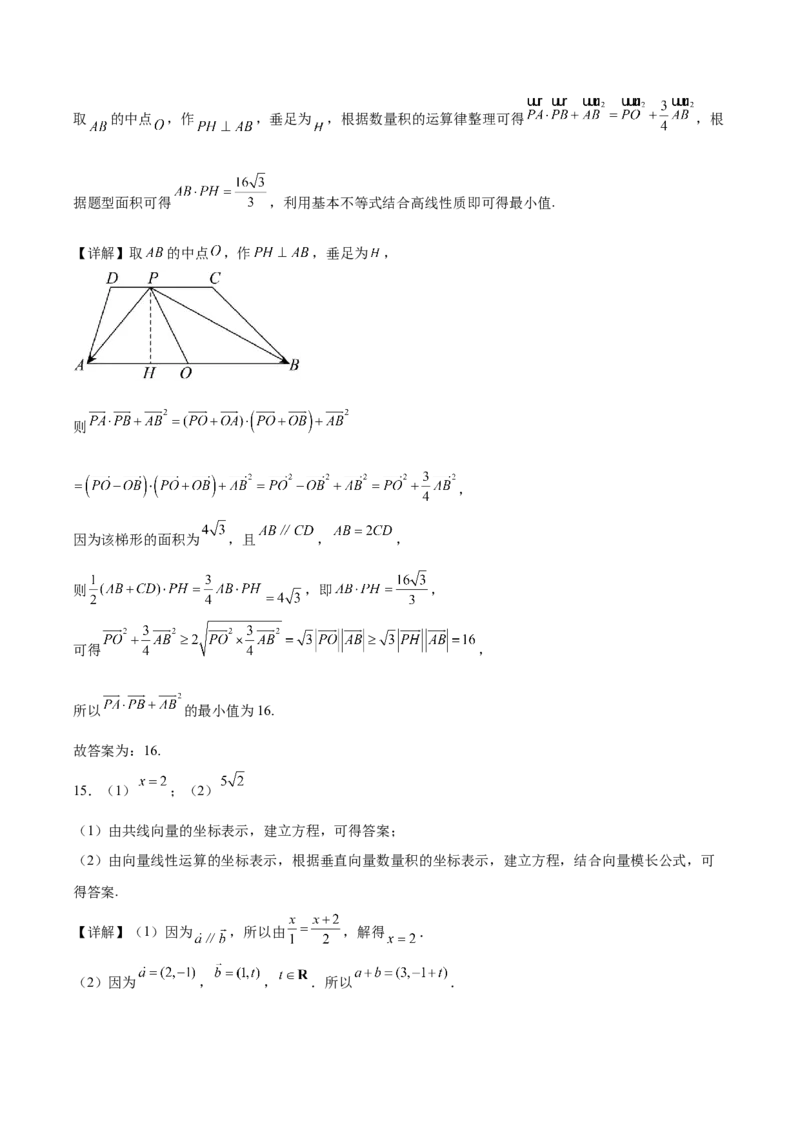
利用三角函数图象以及函数图象变换,画出函数图象,结合图象判断.
【详解】结合三角函数图象与图象变换,依次画出①②③④⑤的函数图象,由图象可知,②⑤不是周期函数,故②⑤不符合;
①③④均为偶函数,最小正周期为 ,对称轴为 ,符合所有条件.
故选:B
6.C
利用正弦定理及 有两解,列不等式求边长范围.
【详解】因为 且 , 有两解,
所以 ,得 .
故选:C
7.D
先由对数函数性质直接求出函数定义范围和值域,接着由对数函数单调性和余弦函数单调性结合定义将问
题转化成求函数 在 上的减区间即可直接计算得解.
【详解】由题 ,则 ,即 ,
又 为 上的增函数,且 ,所以所求函数值域为 ;函数 的单调递减区间即为函数 在
上的减区间,
所以 ,解得所求单调递减区间为 .
故选:D
8.A
【详解】作出图形如图所示,扇形 ,设半径为1, ,
设 , ,由图可知 ,
又 ,
所以 ,所以 ,
由 , ,得 . ,
,故 .
故选:A.
9.ABD
由 可判断A,由弧度制的概念可判断B,由各个象限三角函数符号可判断C,由正切函数对称中心的
概念可判断D.
【详解】对于A,函数 是周期函数,但没有最小正周期,故A正确;对于B,易知分针转过的角是 ,故B正确;
对于C,由 , 可得: , ,
所以 一定为第三象限角,故C错误;
对于D,由 ,可知 是函数 图象的一个对称中心,故D正确.
故选:ABD
10.BCD
对于A,向量不能比较大小;对于B,利用数量积的定义和等腰三角形的性质即可判断;
对于C,利用数量积为负同时要排除反向共线即平角的情况即可判断;
对于D,由正弦定理和大边(角)对大角(边)即可判断.
【详解】对于A,因为向量有方向,所以不能像实数一样比较大小,故A错误;
对于B, ,故B正确;
对于C,由 即
解得 ,故C正确;
对于D,由正弦定理 ,可知 ,故D正确.
故选:BCD.
11.BD
利用函数的周期性的定义,计算并判断A,B;利用正弦函数的值域,计算并判断C;利用函数图象,数形
结合分析两个函数图象的交点,可判断D.
【详解】对于A,因为 的最小正周期是 ,即 ,
所以 ,所以函数 是周期函数,最小正周期是 ,故A
正确;对于B,因为 ,则 ,
所以 不是函数 的最小正周期,故B错误;
对于C,因为 ,所以 , ,
所以当 时, ;当 时, ,则 ,故C正确;
对于D,函数 的零点就是函数 与 的图象的交点,
其中,函数 是周期为1的函数,其值域为 ,
当 时,函数 与 的图象如下,
由图象可知,它们在 内有6个交点,故D错误.
故选:BD.
12. /
由条件结合数量积定义求 ,再利用数量积的运算律结合向量模的性质求 , , ,再利用向量
夹角公式求结论.
【详解】由已知 , ,
所以 ,
又 , ,
所以 ,
,,
设向量 , 的夹角为 ,
所以 .
又因为 ,所以 .
所以向量 , 的夹角为 .
故答案为: .
13.
利用换元法,分离参变量,构造两个函数图象有交点问题,即可求参数范围.
【详解】令 ,则 ,
原方程可转化为关于 的方程 在 上有解,
分离参变量得: ,
即等价于直线 与函数 的图象在 内有交点.
又因为 的图象开口向下,对称轴为直线 ,
所以 在 上单调递增,在 上单调递减,
所以 ,即 .
故答案为: .
14.16取 的中点 ,作 ,垂足为 ,根据数量积的运算律整理可得 ,根
据题型面积可得 ,利用基本不等式结合高线性质即可得最小值.
【详解】取 的中点 ,作 ,垂足为 ,
则
,
因为该梯形的面积为 ,且 , ,
则 ,即 ,
可得 ,
所以 的最小值为16.
故答案为:16.
15.(1) ;(2)
(1)由共线向量的坐标表示,建立方程,可得答案;
(2)由向量线性运算的坐标表示,根据垂直向量数量积的坐标表示,建立方程,结合向量模长公式,可
得答案.
【详解】(1)因为 ,所以由 ,解得 .
(2)因为 , , .所以 .因为 ,所以 ,即 ,解得 ,
即 ,所以 .
16.(1)
(2) .
(1)设该扇形的半径为 ,弧长为 ,可得 ,利用基本不等式可求扇形的面积的最大值;进而可
求圆心角的大小;
(2)由(1)知 , .求得三角形的面积,进而可求弓形的面积.
【详解】(1)设该扇形的半径为 ,弧长为 ,
则 ,
当且仅当 时,等号成立,
此时该扇形的面积 , ,
其圆心角 ,
故所求圆心角 .
(2)由(1)知 , .
又因为两半径与圆心角所对弦构成的三角形面积 ,
所以所求弓形的面积 ,
故所求弓形的面积是 .
17.(1) ;
(2)单调递减区间为 , , , .
【详解】(1)由 的部分图象知,当 时, ,
当 时, ,解得 , .
因为 ,所以 ,则 .因为 且 ,得 ,故 .
(2)将 的图象先向左平移 个单位长度,得到 的图象,
将所有点的横坐标变成原来的 ,纵坐标保持不变,得 的图象.
令 ,整理得 , ,
故 的单调递减区间为 , .
令 ,则 ,故 图象的对称中心为 , .
18.(1)
(2)(i) ;(ii)等边三角形
【详解】(1)因为 是锐角,且 , ,
所以 ,
解得 或 (舍去),所以 ,
由余弦定理得 ,
又 ,则 ,结合 ,
所以 .
(2)(i)由(1)知 , ,
由余弦定理得 ,
即 ,得 ,当且仅当 时,等号成立,
则 ,
即 面积 的最大值为 .
(ii)由(i)可知, 取得最大值时, ,
又 ,所以 为等边三角形.
19.(1) 米, 米.
(2) , .
(3)13个.
(1)由图,结合几何性质与三角函数可得答案;
(2)由图可得 ,后由(1)可得答案;
(3)由(2)及 可得 .设改造后停车位数量最大值为 ,由图可得第 个车位顶点 到
的距离 ,后结合 可得 ,即可得答案.
【详解】(1)由题意得 米, 米, ,
则 ,即 .
由 ,且 , ,可得 , ,
则 米, 米.
(2)由(1)可得 , ,
,
故 , .(3)由 ,可得 ,即 .
设 ,则 ,
整理得 ,解得 .
由 ,可得 .
当 时,解得 , ,不符合题意;
当 时,解得 , ,符合题意.
设改造后停车位数量的最大值为 ,如图,过停车位顶点 作 的垂线,垂足为 ,
则顶点 到线段 的距离为 .
由图及题意可知 , ,
则 .
因为 ,
所以 , , ,
则 .
由题可知 ,即 ,解得 ,则取 ,
故该路段改造后的停车位比改造前增加了 个.