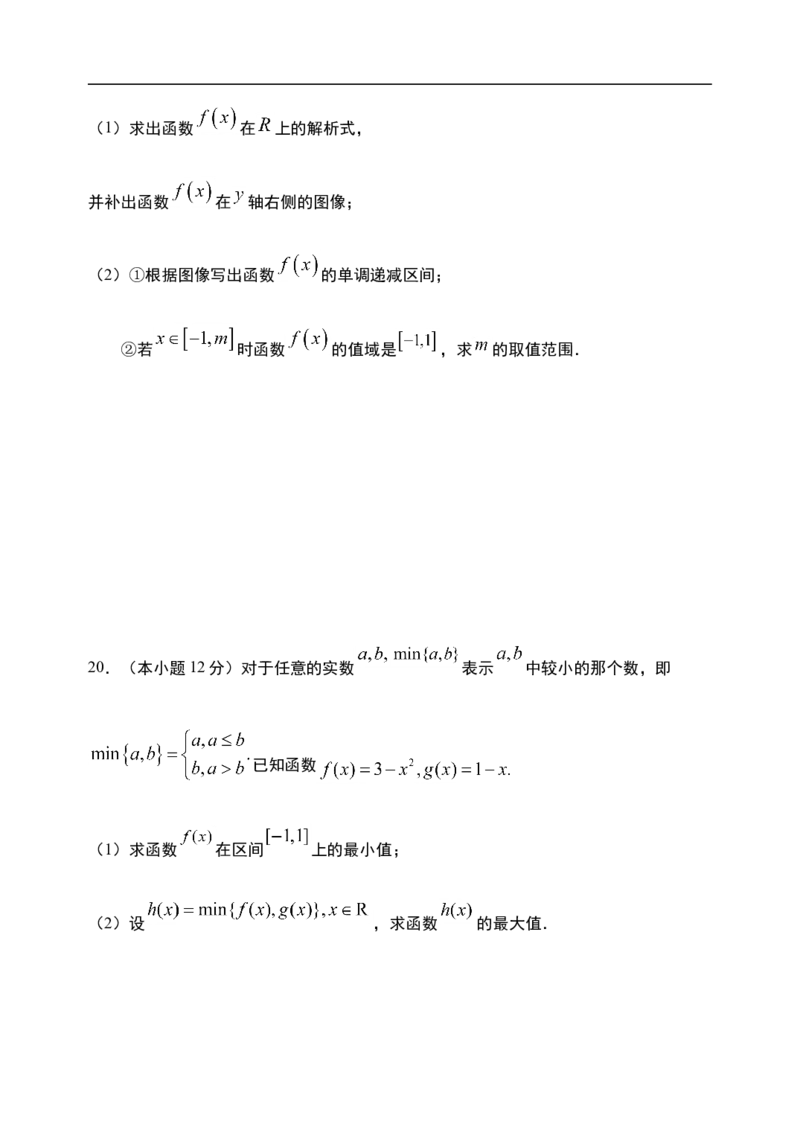文档内容
第三章 函数的概念与性质章末检测
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.函数 的定义域是( )
A. B.
C. D.
2.设 ,则 的值是( )
A.24 B.21
C.18 D.16
3.下列函数中,值域是 的是( )
A. B.
C. D.
4.已知函数 ,则 的解析式为( )
A. B.第三章 函数的概念及性质
C. D.
5.函数 在区间 上为减函数,则a的取值范围为(
)
A. B.
C. D.
6.设 是 上的奇函数,且满足 , ,则 (
)
A. B.
C.0 D.1
7.函数 的图象是圆心在原点的单位圆的两段弧(如图),
则不等式 的解集为( )
A. 或 B. 或
C. 或 D.
- 2 -8.定义在 上的偶函数 ,对任意 ,有
,则( )
A. B.
C. D.
9.已知函数 在 上满足:对任意 ,都有
,则实数 的取值范围是( )
A. B.
C. D.
10.如果奇函数 在区间 上是减函数,且最小值为 3,那么 在区间
上是( )
A.增函数且最小值为3 B.增函数且最大值为3
C.减函数且最小值为-3 D.减函数且最大值为-3
11.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过5000元的
部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计
算:第三章 函数的概念及性质
全月应纳税所得额 税率
不超过3000元的部分 3%
超过3000元至12000元的部分 10%
超过12000元至25000元的部分 20%
有一职工八月份收入12000元,该职工八月份应缴纳个税为( )元
A.1200 B.1040
C.490 D.400
12.已知函数 ,若对一切 , 都成立,则实数a
的取值范围为( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.已知函数 的对应关系如表,函数 的图象如图所示的曲线 ,
其中 , , ,则 的值为______.
1 2 3
2 3 2
- 4 -14.已知函数 的图象关于 对称,当 时, 单调递增,则不等式
的解集为_____________.
15.函数 是区间 上的增函数,则 的取值范围是
____.
16.对于定义在R上的函数 ,有下述结论:
①若 是奇函数,则 的图象关于点 对称;
②若对 ,有 ,则 的图象关于直线 对称;
③若函数 的图象关于直线 对称,则 为偶函数;
④函数 与函数 的图象关于直线 对称.
其中正确结论的序号为________.
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)第三章 函数的概念及性质
17.(本小题10分)已知函数
(1)求 的值;
(2)若 ,求 .
18.(本小题12分) 已知函数 ,且 .
(1)求实数m的值,并判断 的奇偶数;
(2)函数 在 上是增加的还是减少的?并证明.
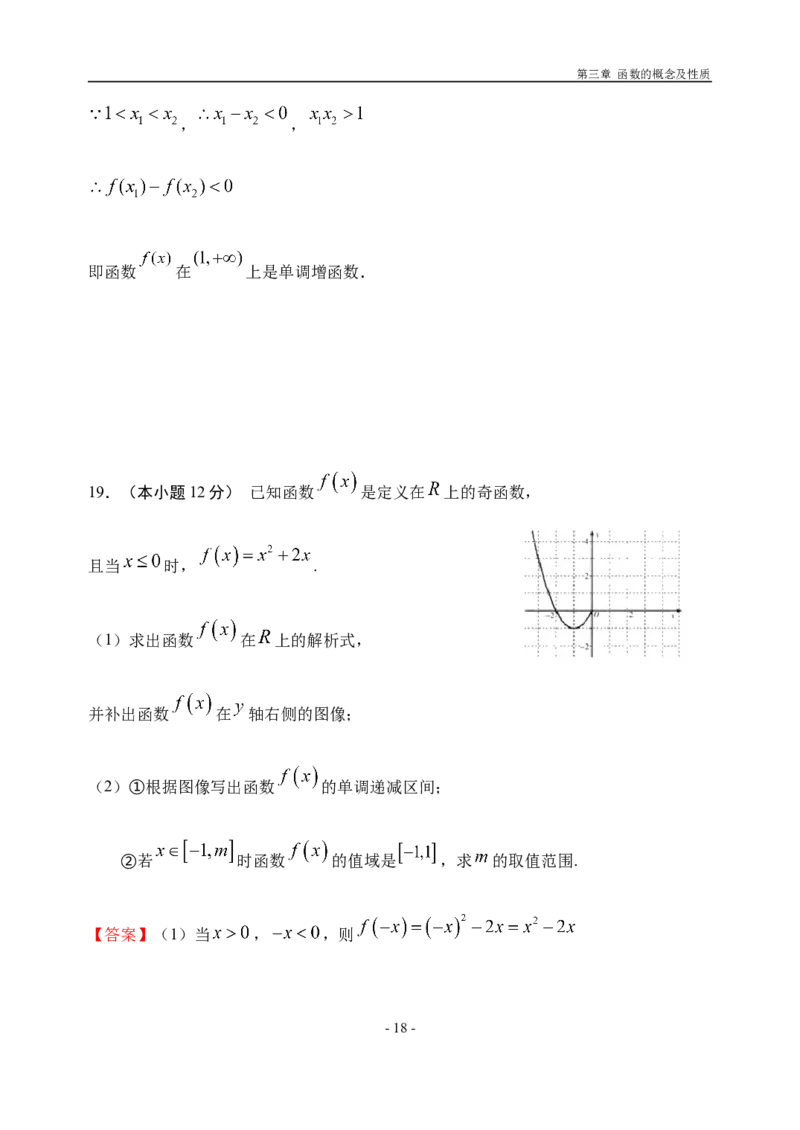
19.(本小题12分) 已知函数 是定义在 上的奇函数,
且当 时, .
- 6 -(1)求出函数 在 上的解析式,
并补出函数 在 轴右侧的图像;
(2)①根据图像写出函数 的单调递减区间;
②若 时函数 的值域是 ,求 的取值范围.
20.(本小题12分)对于任意的实数 表示 中较小的那个数,即
已知函数
(1)求函数 在区间 上的最小值;
(2)设 ,求函数 的最大值.第三章 函数的概念及性质
21.(本小题 12 分)已知定义在 上的奇函数 是增函数,且
(1)求函数 的解析式;
(2)解不等式 .
22.(本小题12分) 美国对中国芯片的技术封锁激发了中国“芯”的研究热潮.某公司
- 8 -研发的 , 两种芯片都已经获得成功.该公司研发芯片已经耗费资金 千万元,现在
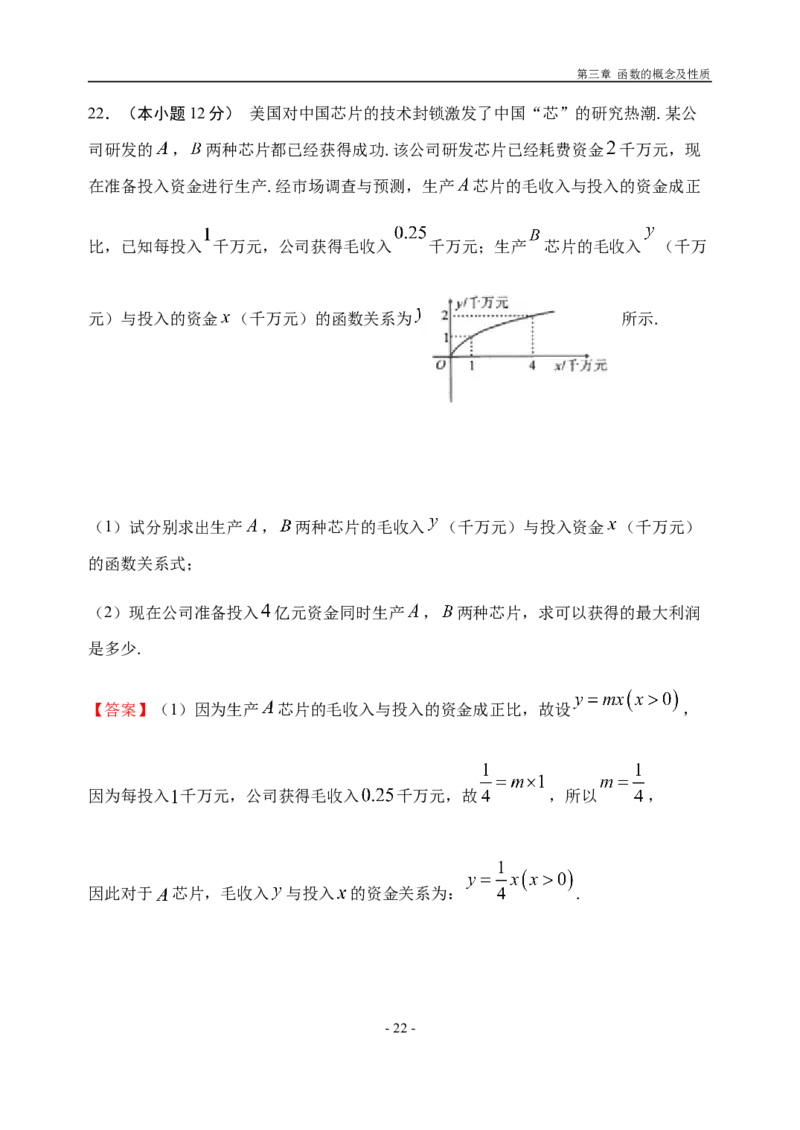
准备投入资金进行生产.经市场调查与预测,生产 芯片的毛收入与投入的资金成正比,
已知每投入 千万元,公司获得毛收入 千万元;生产 芯片的毛收入 (千万元)
与投入的资金 (千万元)的函数关系为 ,其图像如图所示.
(1)试分别求出生产 , 两种芯片的毛收入 (千万元)与投入资金 (千万元)
的函数关系式;
(2)现在公司准备投入 亿元资金同时生产 , 两种芯片,求可以获得的最大利润
是多少.
第三章 函数的概念与性质章末检测
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.函数 的定义域是( )第三章 函数的概念及性质
A. B.
C. D.
【答案】C
2.设 ,则 的值是( )
A.24 B.21
C.18 D.16
【答案】A
3.下列函数中,值域是 的是( )
A. B.
C. D.
【答案】D
4.已知函数 ,则 的解析式为( )
A. B.
C. D.
【答案】B
- 10 -5.函数 在区间 上为减函数,则a的取值范围为(
)
A. B.
C. D.
【答案】B
6.设 为定义在 上的奇函数,且满足 , ,则
( )
A. B.
C.0 D.1
【答案】B
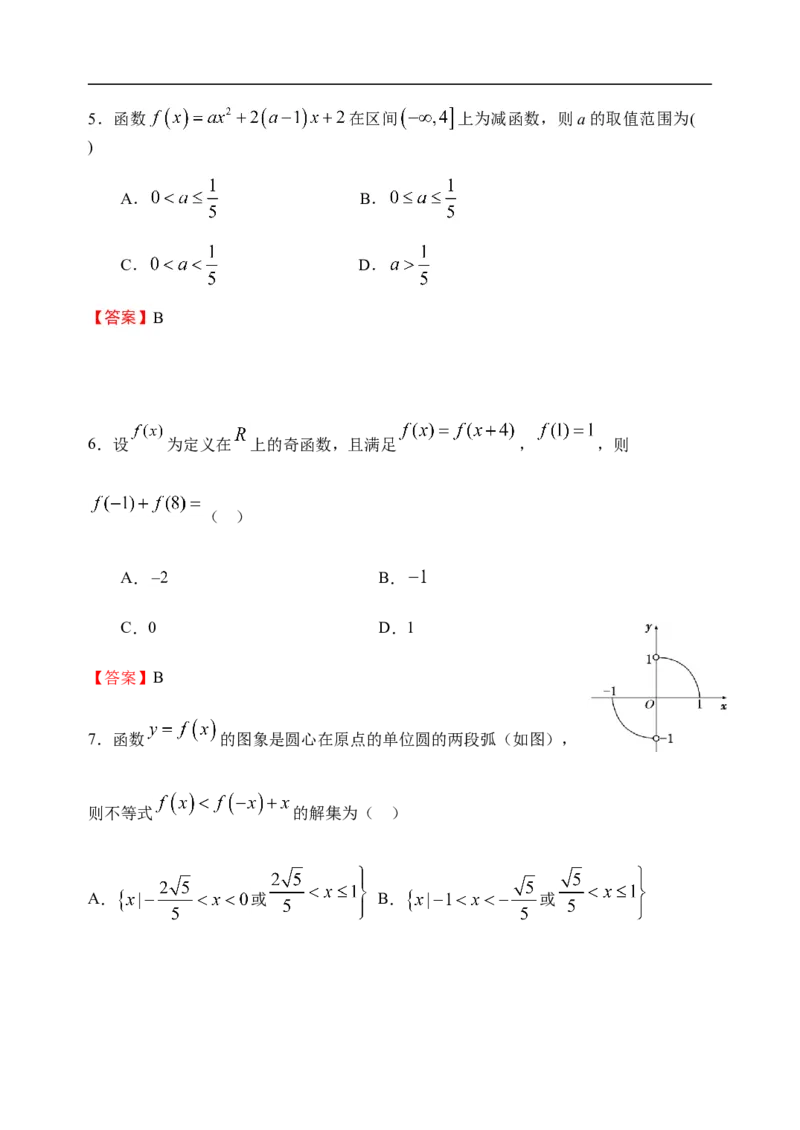
7.函数 的图象是圆心在原点的单位圆的两段弧(如图),
则不等式 的解集为( )
A. 或 B. 或第三章 函数的概念及性质
C. 或 D.
【答案】A
8.定义在 上的偶函数 ,对任意 ,有
,则( )
A. B.
C. D.
【答案】A
9.已知函数 在 上满足:对任意 ,都有
,则实数 的取值范围是( )
A. B.
C. D.
【答案】C
- 12 -10.如果奇函数 在区间 上是减函数,且最小值为 3,那么 在区间
上是( )
A.增函数且最小值为3 B.增函数且最大值为3
C.减函数且最小值为-3 D.减函数且最大值为-3
【答案】D
11.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过5000元的
部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计
算:
全月应纳税所得额 税率
不超过3000元的部分 3%
超过3000元至12000元的部分 10%
超过12000元至25000元的部分 20%
有一职工八月份收入12000元,该职工八月份应缴纳个税为( )元
A.1200 B.1040
C.490 D.400
【答案】C
12.已知函数 ,若对一切 , 都成立,则实数a
的取值范围为( )第三章 函数的概念及性质
A. B.
C. D.
【答案】C
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.已知函数 的对应关系如表,函数 的图象如图所示的曲线 ,
其中 , , ,则 的值为______.
1 2 3
2 3 2
【答案】1
14.已知函数 的图象关于 对称,当 时, 单调递增,则不等式
- 14 -的解集为_____________.
【答案】
15.函数 是区间 上的增函数,则 的取值范围是
____.
【答案】函数f(x)=(t>0)的图象如图:
因为函数f(x)=(t>0)是区间(0,+∞)上的增函数,
所以t≥1.
16.对于定义在R上的函数 ,有下述结论:
①若 是奇函数,则 的图象关于点 对称;
②若对 ,有 ,则 的图象关于直线 对称;
③若函数 的图象关于直线 对称,则 为偶函数;
④函数 与函数 的图象关于直线 对称.
其中正确结论的序号为________.
【答案】若f(x)为奇函数,则f(x-1)=-f(1-x),故①正确.
令t=x-1,则由f(x+1)=f(x-1)可知,f(t)=f(t+2),即f(x)=f(x+2),其图象不一定关
于直线x=1对称.例如,函数f(x)=-(其中[x]表示不超过x的最大整数),第三章 函数的概念及性质
其图象如图所示,满足f(x+1)=f(x-1),但其图象不关于直线x=1对称,故②不正确.
若g(x)=f(x-1)的图象关于直线x=1对称,则有g(x+1)=g(-x+1),即f(x)=f(-x),
∴③正确.
对于④,不妨令f(x)=x,则f(1+x)=1+x,f(1-x)=1-x,二者图象关于x=0对称,故
④错误.
【答案】①③
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)
17.(本小题10分)已知函数
(1)求 的值;
(2)若 ,求 .
【答案】(1)∵-2<-1,∴f(-2)=2×(-2)+3=-1,
∴f(f(-2))=f(-1)=2,
∴f(f(f(-2)))=f(2)=1+=.
(2)当a>1时,f(a)=1+=,∴a=2>1;
- 16 -当-1≤a≤1时,f(a)=a2+1=,∴a=±∈[-1,1];
当a<-1时,f(a)=2a+3=,∴a=->-1(舍去).
综上,a=2或a=±.
18.(本小题12分) 已知函数 ,且 .
(1)求实数m的值,并判断 的奇偶数;
(2)函数 在 上是增加的还是减少的?并证明.
【答案】(1)由题意 , ,所以 ,定义域为
因为 ,所以 是奇函数;
(2)函数 在 上是单调增函数,下用定义法证明
设任意的 , ,且第三章 函数的概念及性质
, ,
即函数 在 上是单调增函数.
19.(本小题12分) 已知函数 是定义在 上的奇函数,
且当 时, .
(1)求出函数 在 上的解析式,
并补出函数 在 轴右侧的图像;
(2)①根据图像写出函数 的单调递减区间;
②若 时函数 的值域是 ,求 的取值范围.
【答案】(1)当 , ,则
- 18 -因为 为奇函数,则 ,
即 时,
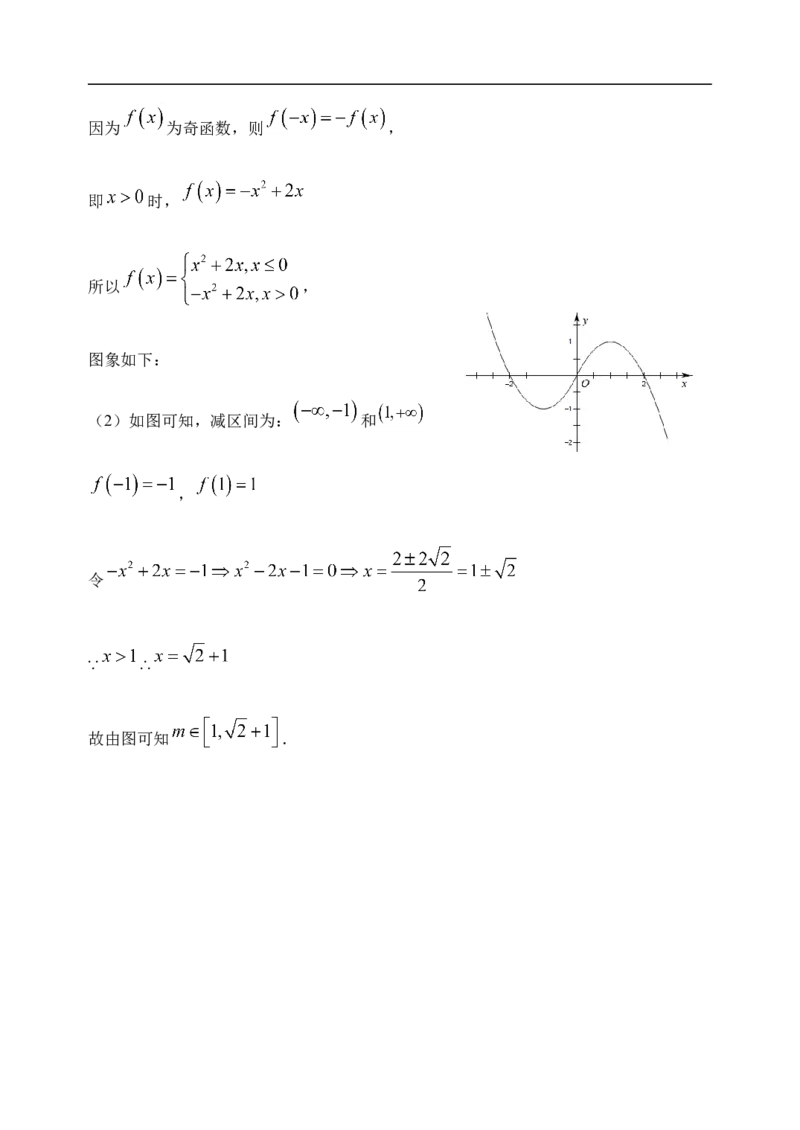
所以 ,
图象如下:
(2)如图可知,减区间为: 和
,
令
∵ ∴
故由图可知 .第三章 函数的概念及性质
20.(本小题12分)对于任意的实数 表示 中较小的那个数,即
已知函数
(1)求函数 在区间 上的最小值;
(2)设 ,求函数 的最大值.
【答案】(1)因为 在 单调递增,在 单调递减,所以 在
上的最小值为 .
又 于是
所以函数 在 上的最小值为2.
(2)当 时,即 时,
当 时,即 或 时,
作出函数 的图象如下图所示,
在 单调递增,
- 20 -在 单调递减.即
当 时, 取到最大值2.
所以函数 的最大值为2.
21.(本小题 12 分)已知定义在 上的奇函数 是增函数,且
(1)求函数 的解析式;
(2)解不等式 .
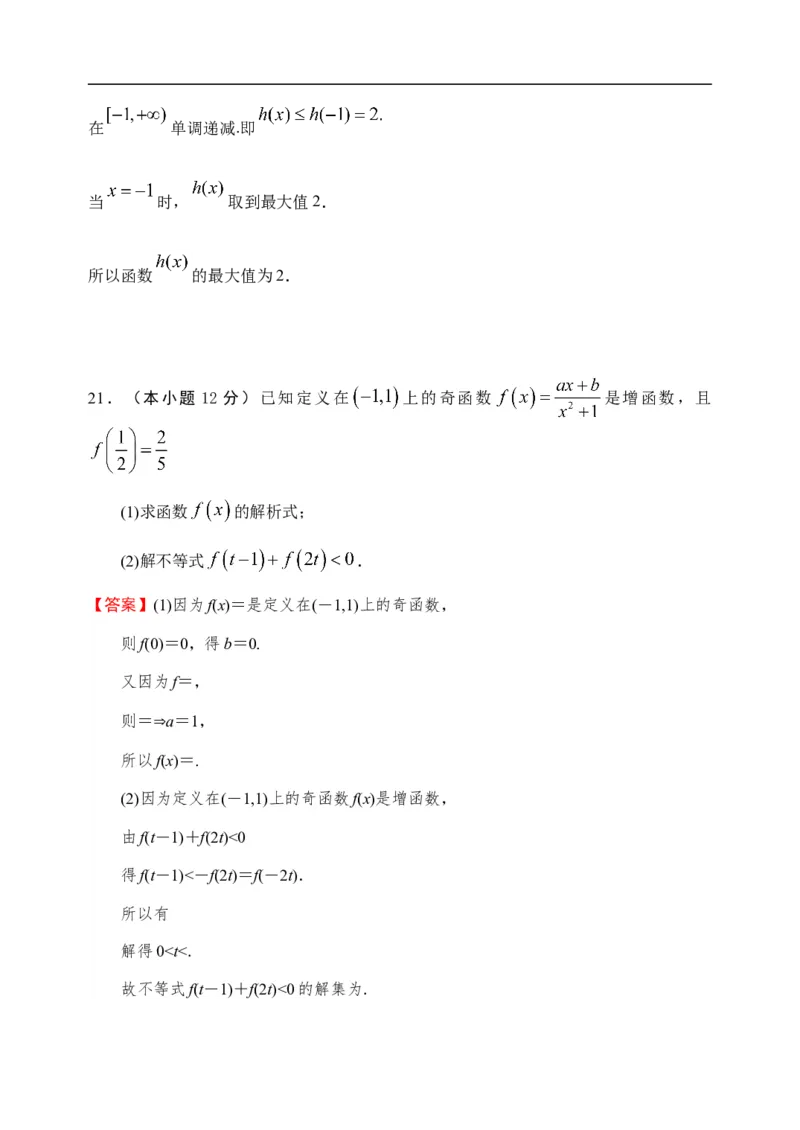
【答案】(1)因为f(x)=是定义在(-1,1)上的奇函数,
则f(0)=0,得b=0.
又因为f=,
则=⇒a=1,
所以f(x)=.
(2)因为定义在(-1,1)上的奇函数f(x)是增函数,
由f(t-1)+f(2t)<0
得f(t-1)<-f(2t)=f(-2t).
所以有
解得0