文档内容
1996年黑龙江高考理科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题共65分)
一、选择题:本大题共15小题;第(1)1(10)题每小题4分,第(11)1(15)题每小题5分,共65分,在每小题给
出的四个选项中,只有一项是符合题目要求的.
(1)已知全集I=N,集合A={x│x=2n,n∈N},B={x│x=4n,n∈N},则
[Key] C
(1)已知全集I=N,集合A={x│x=2n,n∈N},B={x│x=4n,n∈N},则
[Key] C
2 2
(3)若sin x>cos x,则x的取值范围是
[Key] D
(4)复数 等于
[Key] B
5)如果直线l、m与平面α、β、γ满足:l=β∩γ,l//α,m α和m⊥γ那么必有
(A)α⊥γ且l⊥m (B)α⊥γ且m∥β
(C)m∥β且l⊥m (D)α∥β且α⊥γ
[Key] A
(6)当 ,函数 的
(A)最大值是1,最小值是-1
(B)最大值是1,最小值是-(1/2)
(C)最大值是2,最小值是-2
(D)最大值是2,最小值是-1
[Key] D
(7)椭圆 的两个焦点坐标是(B)
第1页 | 共10页(A)(-3,5),(-3,-3) (B)(3,3,),(3,-5)
(C)(1,1,),(-7,1) (D)(7,-1,),(-1,-1)
(8)若 ,则 等于
[Key] A
(9)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为
[Key] D
(10)等比数列{an}的首项a1=-1,前n项的和为Sn,若 ,则 等于
[Key] B
(11)椭圆的极坐标方程为 ,则它在短轴上的两个顶点的极坐标是
[Key] C
(12)等差数列{a 的前m项和为30,前2m项和为100,则它的前3m项和为
n
(A)130 (B)170 (C)210 (D)260
[Key] C
(13)设双曲线 的半焦距为c,直线l过两点(a,0)(0,b)。已知原点到直线l的距离为
,则双曲线的离心率为
[Key] A
(14)母线长为1的圆锥体积最大时,其侧面展开图圆心角ψ等于
[Key] D
第2页 | 共10页(15)设f(x)是(-∞,+∞)上的奇函数,f(x+2)=f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于
(A)0.5 (B)-0.5
(C)1.5 (D)-1.5
[Key] B
2 2 2
(16)已知圆x +y -6x-7=0与抛物线y =2px(p>0)的准线相切.则P= .
[Key] 2
(17)正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有
个(用数字作答).
[Key] 32
(18)tg20°+ tg40°+ tg20°tg40°的值是______________
[Key]
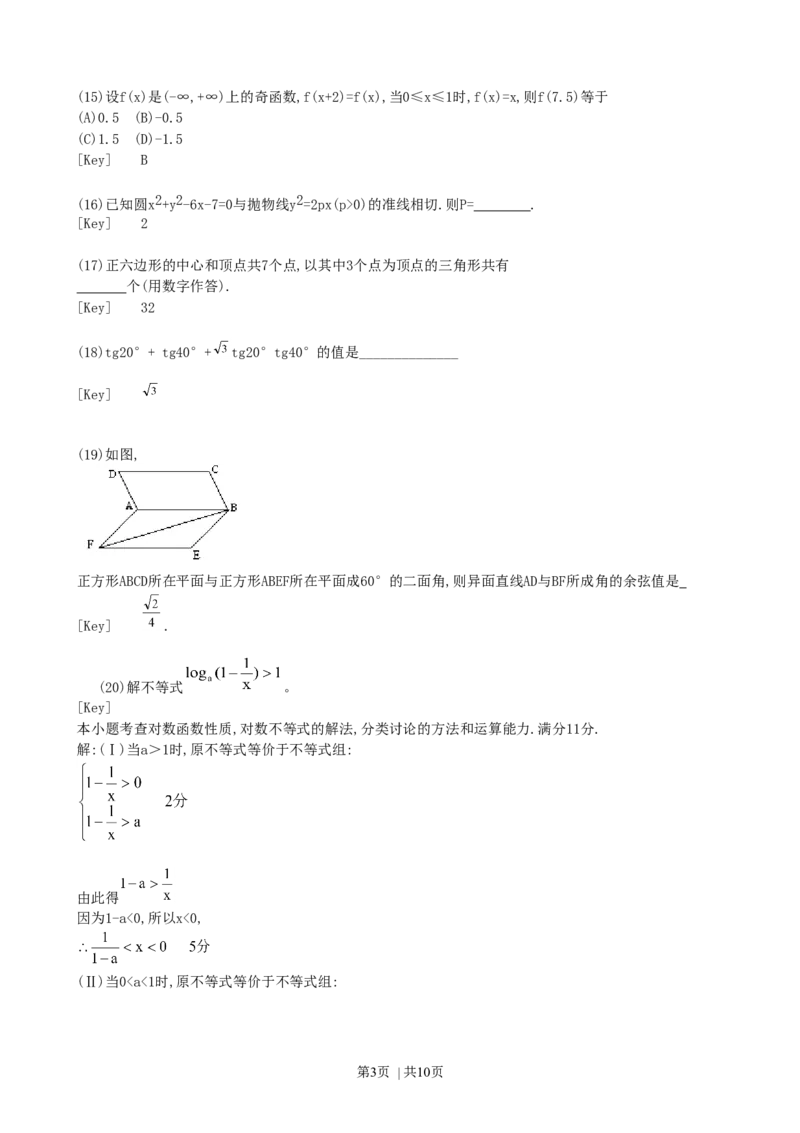
(19)如图,
正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是
[Key] .
(20)解不等式 。
[Key]
本小题考查对数函数性质,对数不等式的解法,分类讨论的方法和运算能力.满分11分.
解:(Ⅰ)当a>1时,原不等式等价于不等式组:
由此得
因为1-a<0,所以x<0,
(Ⅱ)当01或x<0,
由(2)得,01时,不等式的解集为
当00,当-1≤x≤1时,g(x)的最大值为2,求f(x).
[Key] 本小题主要考查函数的性质、含有绝对值的不等式的性质,以及综合运用数学知识分析问题
与解决问题的能力。满分12分.
(Ⅰ)证明:由条件当-1≤x≤1时,│f(x)│≤1,取x=0得
│c│=│f(0)│≤1,
即│c│≤1. 2分
(Ⅱ)证法一:
当a>0时,g(x)=ax+b在[-1,1]上是增函数,
∴g(-1)≤g(x)≤g(1),
∵│f(x)│≤1(-1≤x≤1),│c│≤1,
∴g(1)=a+b=f(1)-c≤│f(1)│+│c│≤2,
g(-1)=-a+b=-f(-1)+c≥-(│f(-1)│+│c│≥-2,
由此得│g(x)│≤2; 5分
当a<0时,g(x)=ax+b在[-1,1]上是减函数,
∴g(-1)≥g(x)≥g(1),
∵│f(x)│≤1(-1≤x≤1),│c│≤1,
∴g(-1)=-a+b=-f(-1)+c≤│f(-1)│+│c│≤2,
g(1)=a+b=f(1)-c≥-(│f(1)│+│c│)≥-2,
由此得│g(x)│≤2; 7分
当a=0时,g(x)=b,f(x)=bx+c.
∵-1≤x≤1,
∴│g(x)│=│f(1)-c│≤│f(1)│+│c│≤2.
综上得│g(x)│≤2. 8分
证法二
第9页 | 共10页根据含绝对值的不等式的性质,得
即 │g(x)│≤2. 8分
(Ⅲ)因为a>0,g(x)在[-1,1]上是增函数,当x=1时取得最大值2,
即g(1)=a+b=f(1)-f(0)=2.①
∵-1≤f(0)=f(1)-2≤1-2=-1,
∴c=f(0)=-1. 10分
因为当-1≤x≤1时,f(x)≥-1,即f(x)≥f(0),
根据二次函数的性质,直线x=0为f(x)的图象的对称轴,由此得
由① 得a=2.
2
所以 f(x)=2x -1. 12分
第10页 | 共10页