文档内容
浙江省台州市台州十校 2024-2025 学年高一上学期 11 月期中联考数学
试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的)
1.设集合 ,集合 ,则集合 ( )
A. B. C. D.
2.命题“ ”的否定是( )
A. B. C. D.
3.函数 的定义域为( )
A. B. C. D.
4.已知a,b为实数,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
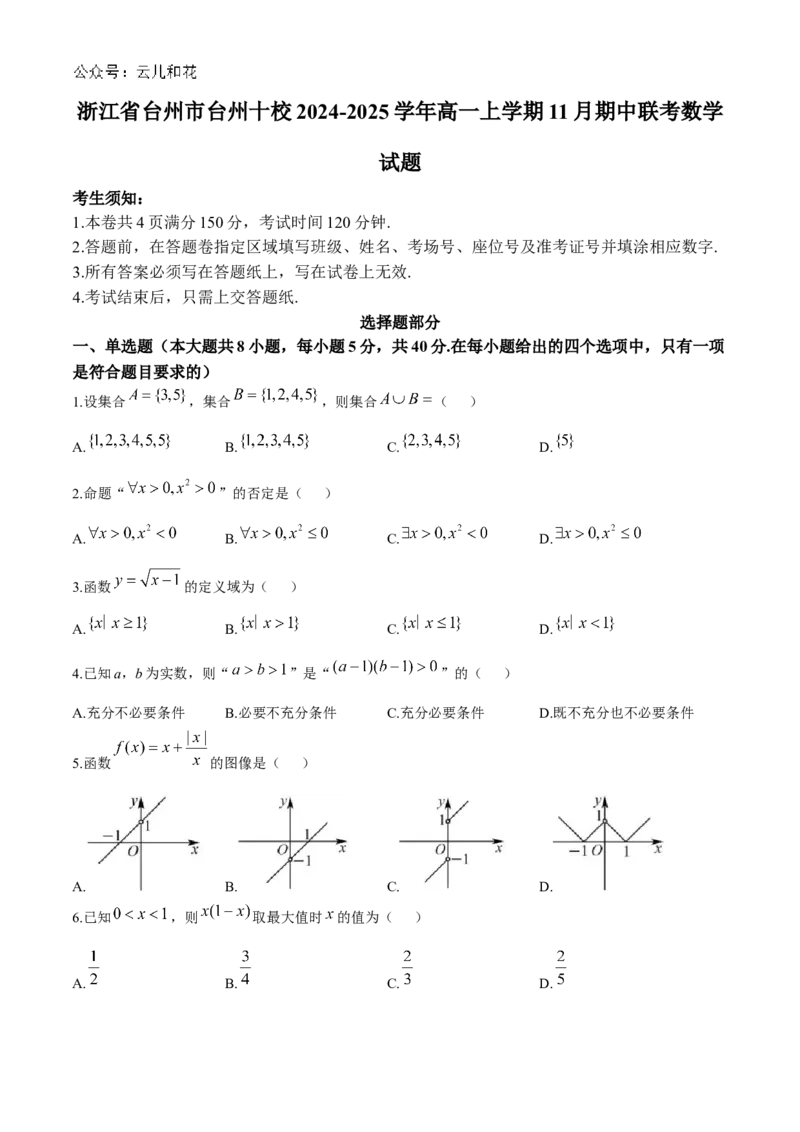
5.函数 的图像是( )
A. B. C. D.
6.已知 ,则 取最大值时 的值为( )
A. B. C. D.7.不等式 的解集是 ,则 的解集是( )
A. B. C. D.
8.已知“不小于 的最小的整数”所确定的函数通常记为 ,例如: ,则方程
的正实数根的个数是( )
A.1个 B.2个 C.3个 D.无数个
二、多选题(本大题共3小题,每小题6分,共18分.每小题各有四个选项,有多个选项正
确)
9.设x,y为实数,满足 ,则下列结论正确的是( )
A. B. C. D.
10.下列各组函数中,两个函数为同一函数的是( )
A. 和 B. 和
C. 和 D. 和
11.定义在R上的函数 满足 ,当 时, ,则下列说法正确的是
( )
A. B. 为奇函数
C. 在区间[m,n]上有最大值 D. 的解集为
非选择题部分
三、填空题(本大题共3小题,每小题5分,共15分)
12.已知函数 则 _____________.
13.已知正数x,y满足: ,则 的最小值为_____________.
14.已知函数 ,若对任意的 ,总存在 ,使成立,则实数 的取值范围是_____________.
四、解答题(共5小题,共77分.解答题应写出文字说明,证明过程或演算步骤)
15.(13分)已知集合
(1)若 ,求 ;
(2)若 ,求实数 的取值范围.
16.(15分)设函数 ,其图像过点
(1)求出 的解析式;
(2)判断函数 在 上的单调性,并用定义证明.
17.(15分)某租赁公司,购买了一辆小型挖掘机进行租赁.据市场分析,该小型挖掘机的租赁利润 (单
位:万元)与租赁年数 的关系为 .
(1)该挖掘机租赁到哪几年时,租赁的利润超过9万元?
(2)该挖掘机租赁到哪一年时,租赁的年平均利润最大?
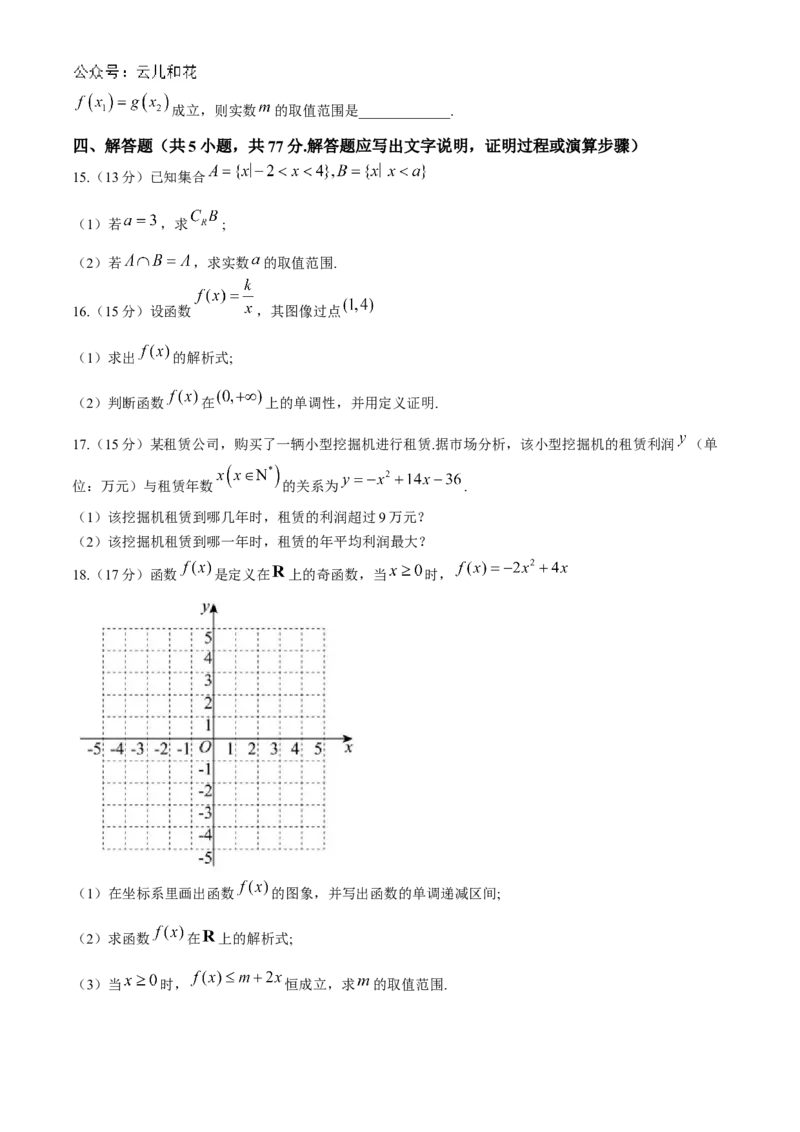
18.(17分)函数 是定义在 上的奇函数,当 时,
(1)在坐标系里画出函数 的图象,并写出函数的单调递减区间;
(2)求函数 在 上的解析式;
(3)当 时, 恒成立,求 的取值范围.19.(17分)已知函数
(1)若 ,判断 的奇偶性,求 的最大值;
(2)若 的最大值为 ,求 的最小值.2024 学年第一学期台州十校联盟期中联考
高一年级数学参考答案
命题:坎门中学 林勤 审稿:新桥中学 茹福生
一、单选题:
BDAA CADB
二、多选题
9.AC 10.AB 11.ABD
三、填空题:
12.2 13. 14.
四、解答题:
15.解:(1)因为 ,
所以 ;………………………………………………………………………………6分
(2)因为 ,
所以 ,
所以实数 的取值范围为 ………………………………………………………………13分
16.解:(1)将点坐标代入解析式, ,得 .
……………………………………………………………………………………………4分
(2) 在 上的是减函数.…………………………………………………………6分
证明: ,且
则,即 ………………………………………15分
17.解:(1)由题意得 ,……………………………………………………….2分
整理得 ,解得 ,………………………………………………………5分
,则
故该挖掘机租赁到第6,7,8年时,租赁的利润超过9万元……………………………………7分
(2)租赁的年平均利润为 …………………………………………………10分
,
因为 ,
所以当且仅当 时,即 时, ,
故该挖掘机租赁到第6年时,租赁的年平均利润最大…………………………………………15分
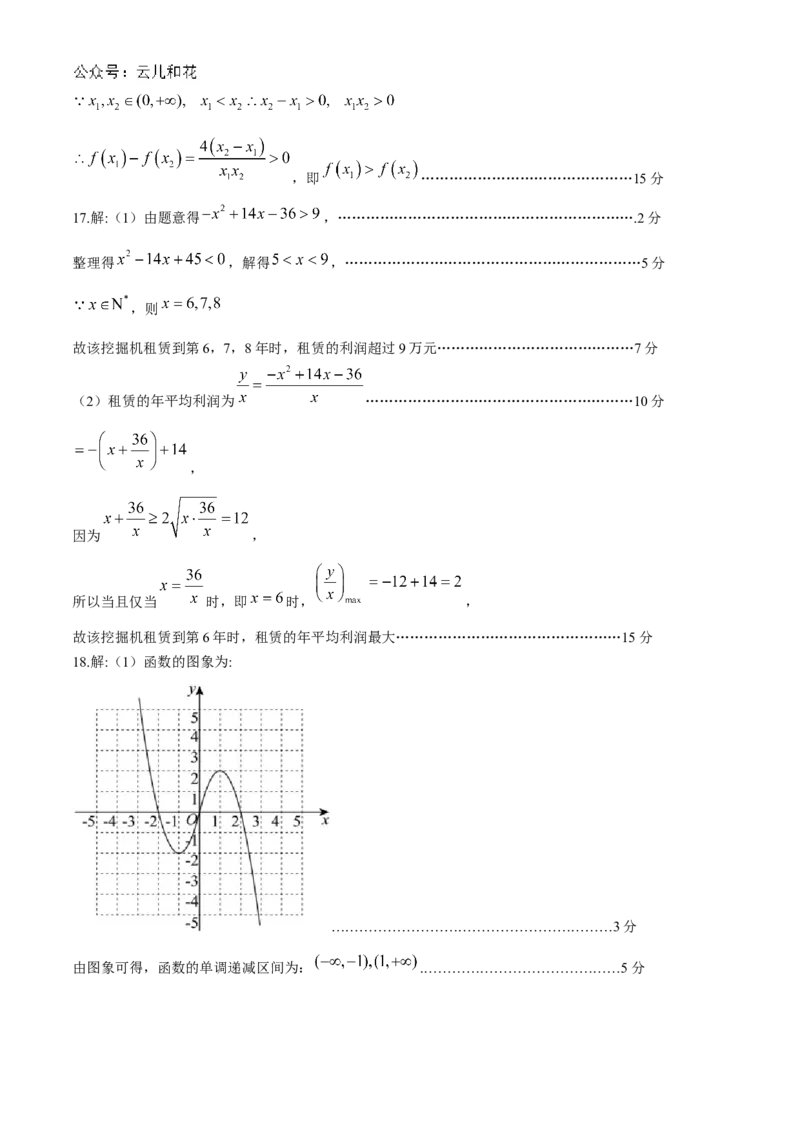
18.解:(1)函数的图象为:
……………………………………………………3分
由图象可得,函数的单调递减区间为: .……………………………………5分(2) 函数 是定义在 上的奇函数,
当 时,有 ,
,
.…………………………………………………………………10分
(3) 当 时, 恒成立,
,
设 ,则当 时, ,
……………………………………………………………………………………17分
19(1)由题意得 ,
当 时, ,
因为 ,所以 是偶函数,
故 的最大值为4.………………………………………………………………………5分
(2)由题意得 ,…………………7分
①若 ,则当 时, 在 上单调递增, ,
当 时, .
因为 ,
所以 .………………………………………………………………10分
②若 ,则当 时, ,
当 时, .因为 ,所以当 时, ,
当 时, .…………………………………………………13分
③若 ,则当 时, ,
当 时, 在 上单调递减, .
因为 ,所以 .……………16分
综上所述,当 时, ,当 时, .
故 的最小值为4.……………………………………………………………………………17分