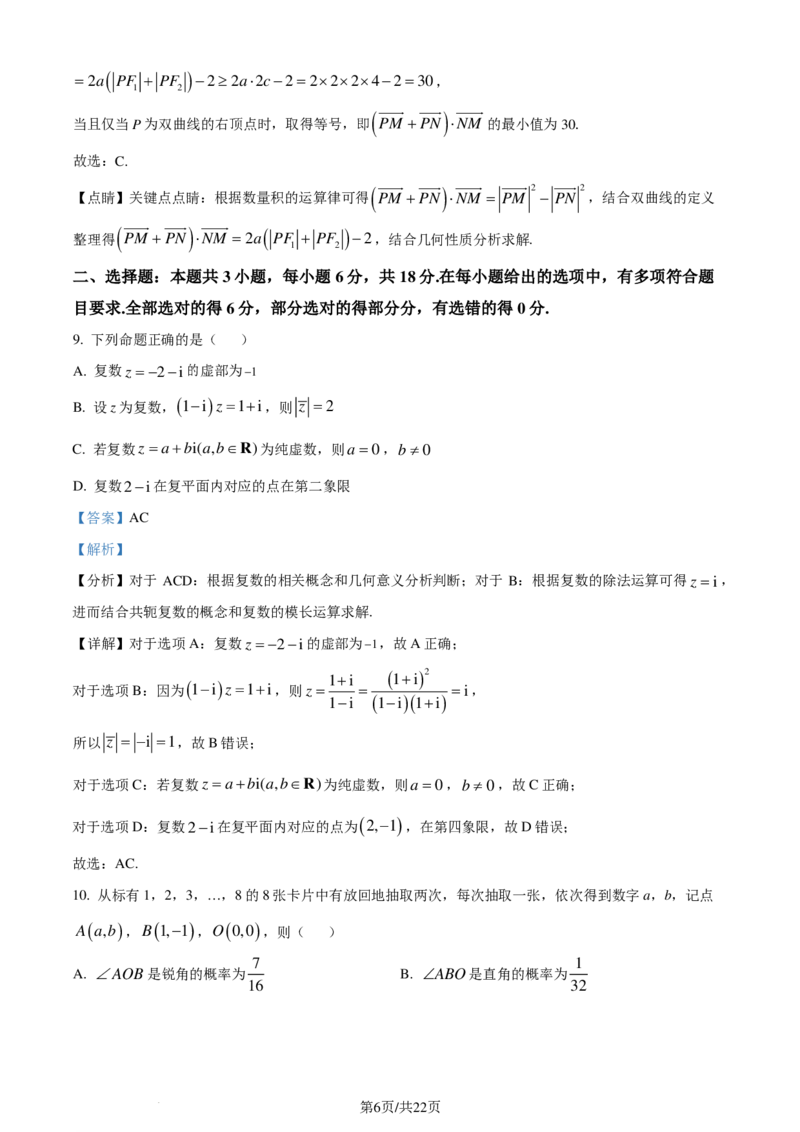山东日照市2024届高三下学期一模数学试题（解析版）(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024届山东日照一模数学试题+答案

2021 级高三模拟考试 数学试题 考生注意： 1．答题前，考生务必将自百的姓名、考生号等填写在答题卡和试卷指定位置上. 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改 动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本 试卷上无效. 3．考试结束，将试题卷和答题卡一并交回. 选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是符 合题目要求的. A= { x|2x2 −x−1≤0 } B={ x|x>0 } AB= 1. 已知集合 ， ，则 （ ）  1   1  A.  − ,1  B.  − ,+∞  C. [ 0,1 ] D. ( 0,1 ]  2   2  【答案】D 【解析】 【分析】根据题意求集合A，再根据交集运算求解. { }  1  【详解】由题意可得：A= x|2x2 −x−1≤0 =x|− ≤ x≤1，  2  所以AB=( 0,1 ] . 故选：D. 2. 已知数列 { a } 是公比为2的等比数列，且a +a =3，则a +a 等于（ ） n 1 2 5 6 A. 24 B. 48 C. 72 D. 96 【答案】B 【解析】 【分析】由等比数列通项公式的性质得出结果. 【详解】因为数列 { a } 是公比为2的等比数列，且a +a =3， n 1 2 所以a a a a q4 324 48， 5 6 1 2 故选：B. 第1页/共22页 学科网（北京）股份有限公司3. 已知样本空间Ω={a,b,c,d}含有等可能的样本点，且A={ a,b } ，B={ b,c } ，则P ( AB ) =（ ） 1 3 1 A. B. C. D. 1 4 2 4 【答案】A 【解析】 【分析】根据题意分别求得P ( A ) ，P(B)，P ( AB ) ，结合独立事件的定义，可判定事件A与B相互独 立，再结合对立事件的概念关系可运算得解. 1 1 1 【详解】由题意，P ( A )= ，P ( B )= ，P ( AB )= ， 2 2 4 ∴P ( AB )= P ( A ) P ( B ) ， 所以事件A与B相互独立，则A与B也相互独立， 1 1 1 ∴P ( AB ) = P ( A ) P ( B ) = P ( A )( 1−P ( B )) = × = . 2 2 4 故选：A. 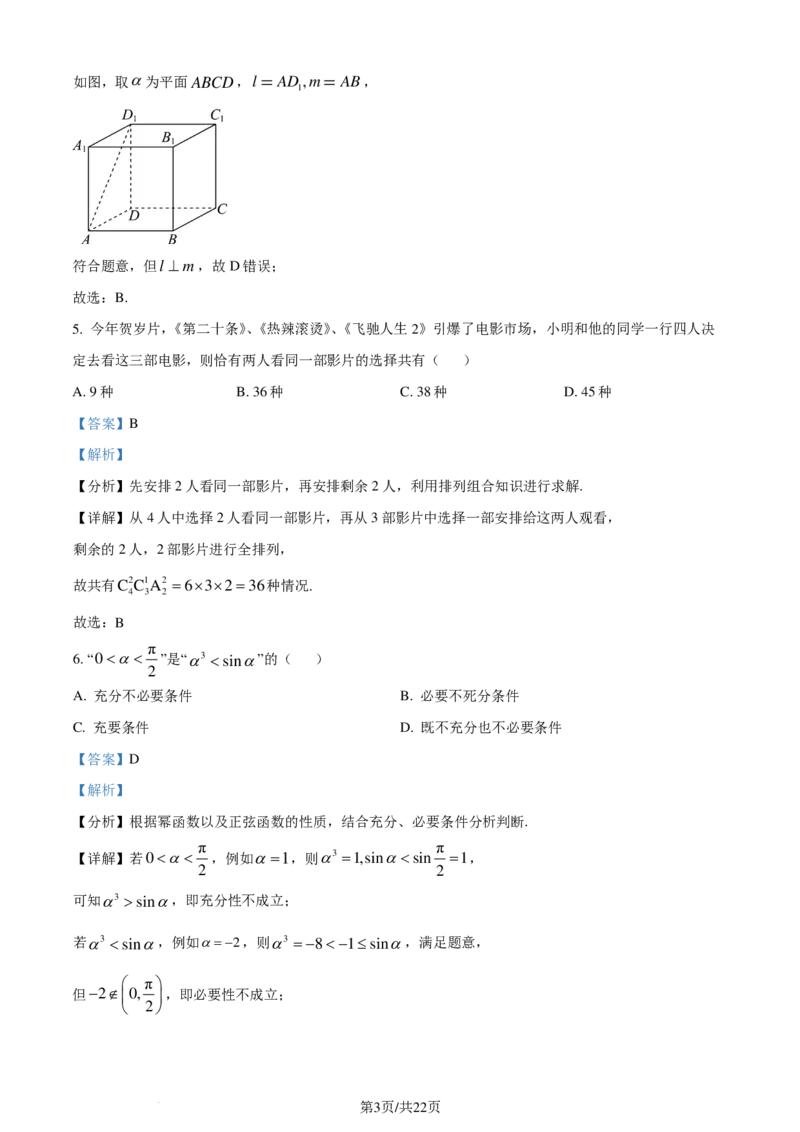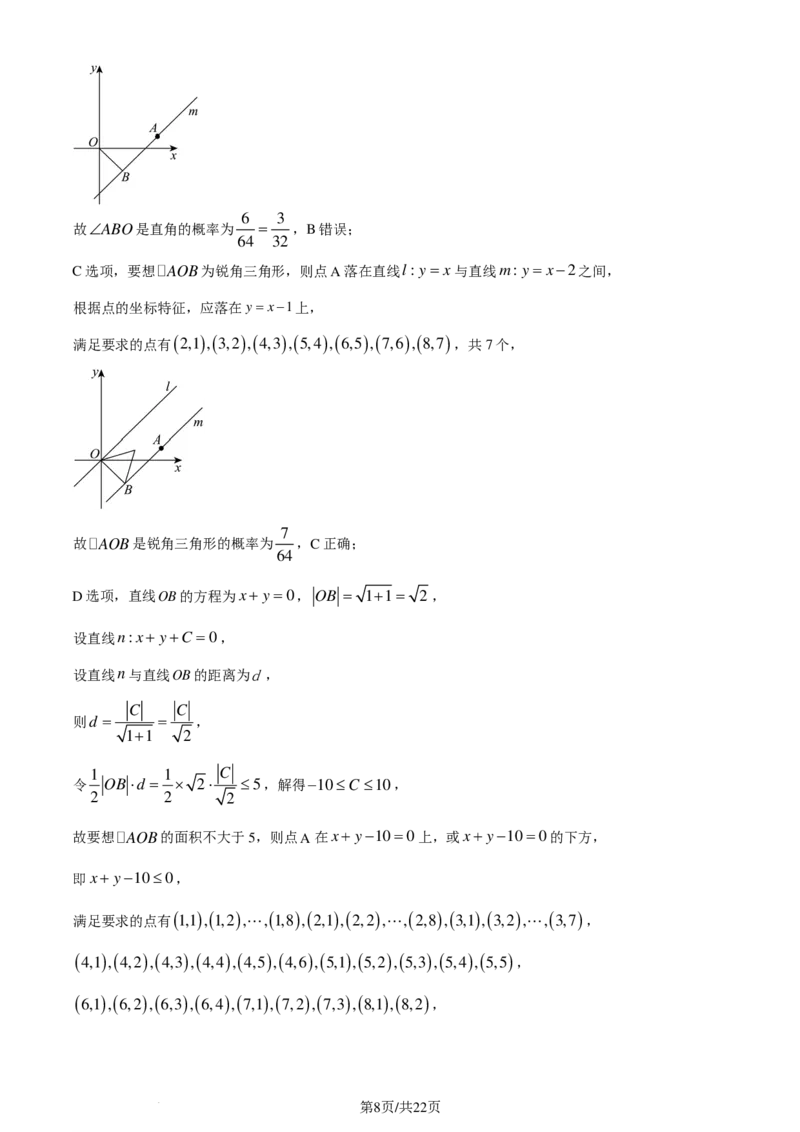4. 已知l，m是两条不同的直线，α为平面，m⊂α，下列说法中正确的是（ ） A. 若l与α不平行，则l与m一定是异面直线 B. 若l∥α，则l与m可能垂直 C. 若lα= A，且A∉m，则l与m可能平行 D. 若lα= A，且l与α不垂直，则l与m一定不垂直 【答案】B 【解析】 【分析】根据空间中线、面位置关系分析逐项分析判断. 【详解】对于选项A：若l与α不平行，则l与α的位置关系有：相交或直线在平面内， 且m⊂α，则l与m的位置关系有：平行、相交或异面，故A错误； 对于选项B：若l∥α，则l与m可能垂直， 如图所示：l∥l′,l′⊂α,l′⊥m，可知：l ⊥m，故B正确； 对于选项C：若lα= A，且A∉m，m⊂α，则l与m异面，故C错误； 对于选项D：若lα= A，且l与α不垂直，则l与m可能垂直， 第2页/共22页 学科网（北京）股份有限公司如图，取α为平面ABCD，l AD,m AB， 1 符合题意，但l ⊥m，故D错误； 故选：B. 5. 今年贺岁片，《第二十条》、《热辣滚烫》、《飞驰人生2》引爆了电影市场，小明和他的同学一行四人决 定去看这三部电影，则恰有两人看同一部影片的选择共有（ ） A. 9种 B. 36种 C. 38种 D. 45种 【答案】B 【解析】 【分析】先安排2人看同一部影片，再安排剩余2人，利用排列组合知识进行求解. 【详解】从4人中选择2人看同一部影片，再从3部影片中选择一部安排给这两人观看， 剩余的2人，2部影片进行全排列， 故共有C2C1A2 =6×3×2=36种情况. 4 3 2 故选：B π 6. “0<α< ”是“α3 sinα，即充分性不成立； 若α3 0，所以 2−2sinB=0,sinB= ， 2 2 π 而B是锐角，所以B= . 4 由余弦定理得 b= a2+c2−2accosB = 25+32−2×5×4 2× 2 = 17. 2 【小问2详解】 a2 +b2 −c2 25+17−32 1 由余弦定理得cosC = = = ，而C是锐角， 2ab 2×5× 17 17 1 4  π 2 所以sinC = 1−cos2C = 1− = ，所以sin(2C+B)=sin2C+  = (sin2C+cos2C). 17 17  4  2 2 ( ) = 2sinCcosC+2cos2C−1 2 2 = 2sinCcosC+ 2cos2C− 2 4 1 1 2 7 2 = 2× × + 2× − =− . 17 17 17 2 34 16. 己知各项均为正数的数列 { a } 的前n项和为S ，且a ，S ，a2成等差． n n n n n { } （1）求a 及 a 的通项公式； 1 n  4  （2）记集合a∣a + ≤2k,k∈N 的元素个数为b ，求数列b 的前50项和．  n n a +  k k n 【答案】（1）a =1，a =n 1 n （2）2497 第13页/共22页 学科网（北京）股份有限公司【解析】 【分析】（1）根据等差中项可得2S =a +a2，结合S 与a 之间的关系分析可知数列 { a } 为等差数列， n n n n n n 再利用等差数列通项公式运算求解； 0,k =0 1 4  （2）根据题意可得k ≥ n+ ，结合基本不等式可得b =1,k =1 ，结合等差数列求和公式运算 2 n k  2k−1,k ≥3 求解. 【小问1详解】 因为a ，S ，a2成等差，则2S =a +a2，且a >0， n n n n n n n 当n=1时，可得2a =a +a2，解得a =1或a =0（舍去）； 1 1 1 1 1 当n≥2时，可得2S =a +a2 ， n−1 n−1 n−1 两式相减得2a =a −a +a2 −a2 ，整理得 ( a +a )( a −a )=( a +a ) ， n n n−1 n n−1 n n−1 n n−1 n n−1 且a +a >0，则a −a =1； n n−1 n n−1 可知数列 { a } 是以首项为1，公差为1的等差数列，所以a =1+n−1=n. n n 【小问2详解】 4 4 1 4 因为a + ≤2k，由（1）可得n+ ≤2k，即k ≥ n+ ， n a n 2 n n 1 4 1 4 4 因为 n+  ≥ ×2 n⋅ =2，当且仅当n= ，即n=2时，等号成立， 2 n 2 n n 可知b =0,b =1； 1 2 1 4  1 2  1 4  1 当k ≥3时，因为 2k−1+  =k−  −  ≤k, 2k+  =k+ >k ， 2 2k−1 2 2k−1 2 2k  k 所以b =2k−1； k 0,k =0  综上所述：b =1,k =1 . k  2k−1,k ≥3 48 ( 5+99 ) 所以数列b 的前50项和为0+1+5+7+⋅⋅⋅+99=1+ =2497. k 2 第14页/共22页 学科网（北京）股份有限公司17. 随着科技的不断发展，人工智能技术的应用领域也将会更加广泛，它将会成为改变人类社会发展的重 要力量．某科技公司发明了一套人机交互软件，它会从数据库中检索最贴切的结果进行应答．在对该交互 软件进行测试时，如果输入的问题没有语法错误，则软件正确应答的概率为80%；若出现语法错误，则软 件正确应答的概率为30%．假设每次输入的问题出现语法错误的概率为10%． （1）求一个问题能被软件正确应答的概率； （2）在某次测试中，输入了n(n≥6)个问题，每个问题能否被软件正确应答相互独立，记软件正确应答 的个数为X，X =k(k =0,1,,n)的概率记为P ( X =k ) ，则n为何值时，P ( X =6 ) 的值最大？ 【答案】（1）0.75 （2）7或8 【解析】 【分析】（1）根据题意结合全概率公式运算求解；  3 3 6 1 n−6 （2）由题意可知：X Bn, 且P ( X =6 )=C6     ，结合数列单调性分析求解.  4 n 4 4 【小问1详解】 记“输入的问题没有语法错误”为事件A，“回答正确”为事件B， 由题意可知：P ( A ) =0.1,P ( B| A )=0.8,P ( B| A ) =0.3，则P ( A )=1−P ( A ) =0.9， 所以P ( B )= P ( B| A ) P ( A ) +P ( B| A ) P ( A )=0.75. 【小问2详解】 3 由（1）可知：P ( B )=0.75= ， 4  3 3 6  3 n−6 3 6 1 n−6 则X Bn, ，可得P ( X =6 )=C6   1−  =C6     ，  4 n 4  4 n 4 4 6 n−5 3 1 C6     3 6 1 n−6 a n+14 4 n+1 令a n =C n 6  4    4   ，则 a n+1 = 3 6 1 n−6 = 4 ( n−5 ) ， n C6     n 4 4 n+1 令 >1，解得n<7，可知当n≤6，可得a >a ； 4 ( n−5 ) n+1 n n+1 令 <1，解得n>7，可知当n≥8，可得a >a ； 4 ( n−5 ) n+1 n 第15页/共22页 学科网（北京）股份有限公司n+1 令 =1，解得n=7，可得a =a ； 4 ( n−5 ) 8 7 所以当n=7或n=8时，a 最大，即n为7或8时，P ( X =6 ) 的值最大. 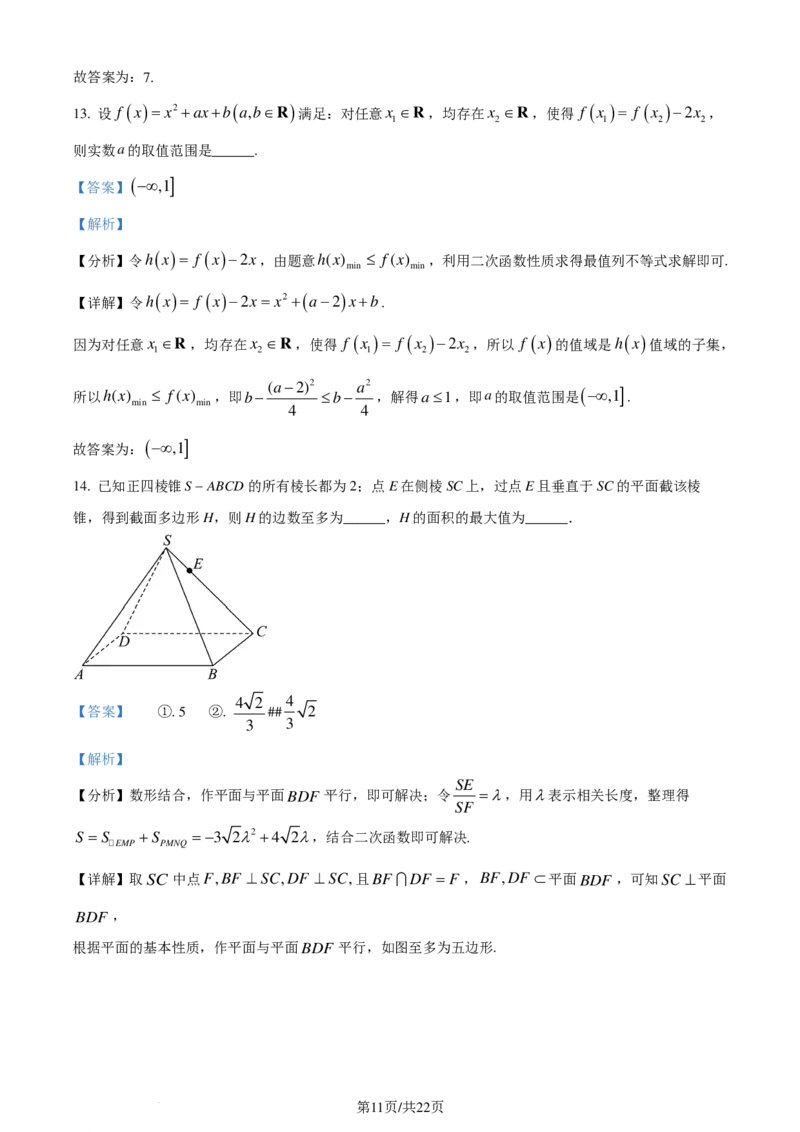n 18. 已知函数 f ( x )=3lnx+ax2 −4x ( a >0 )． ( ) （1）讨论函数 f x 的单调性； 1 （2）当a= 时，若方程 f ( x )=b有三个不相等的实数根x ,x ,x ，且x < x < x ，证明： 1 2 3 1 2 3 2 x −x <4． 3 1 【答案】（1）答案见解析 （2）证明见解析 【解析】 【分析】（1）求导，分∆≤0和∆>0两种情况，结合导数符号判断函数单调性； （2）根据题意分析可知： f ( x ) 在 ( 0,1 ) , ( 3,+∞) 内单调递增，在 ( 1,3 ) 内单调递减， 0< x <1< x <3< x ，利用极值点偏离证明x +x >2和x +x <6，即可得结果. 1 2 3 1 2 2 3 【小问1详解】 由题意可知： f ( x ) 的定义域为 ( 0,+∞) ， f′( x )= 3 +2ax−4= 2ax2 −4x+3 ， x x 且a>0，令 f′( x )=0，可得2ax2 −4x+3=0， 2 当∆=16−24a≤0，即a≥ 时，可知2ax2 −4x+3≥0在 ( 0,+∞) 内恒成立， 3 即 f′( x )≥0在 ( 0,+∞) 内恒成立，所以 f ( x ) 在 ( 0,+∞) 内单调递增； 2 2− 4−6a 2+ 4−6a 当∆=16−24a >0，即00,x x = >0可知00，  x  2−x  x ( 2−x ) 可知g ( x ) 在 ( 0,1 ) 内单调递增，则g ( x )< g ( 1 )=0， 可得 f ( x )< f ( 2−x ) 在 ( 0,1 ) 内恒成立， 因为 0< x <1，则 f ( x )= f ( x )< f ( 2−x ) ， 1 1 2 1 且1<2−x <2,1< x <3， f ( x ) 在 ( 1,3 ) 内单调递减， 1 2 则2−x < x ，即x +x >2； 1 2 1 2 令h ( x )= f ( x )− f ( 6−x ) ,1< x<3， 3   3  6 ( x−3 )2 则g′( x )= f′( x )+ f′( 6−x )=  +x−4 +  +6−x−4 = >0，  x  6−x  x ( 6−x ) 可知h ( x ) 在 ( 1,3 ) 内单调递增，则h(x)3， f ( x ) 在 ( 3,+∞) 内单调递增， 2 3 则6−x > x ，即x +x <6； 2 3 2 3 第17页/共22页 学科网（北京）股份有限公司由x +x >2和x +x <6可得x −x <4. 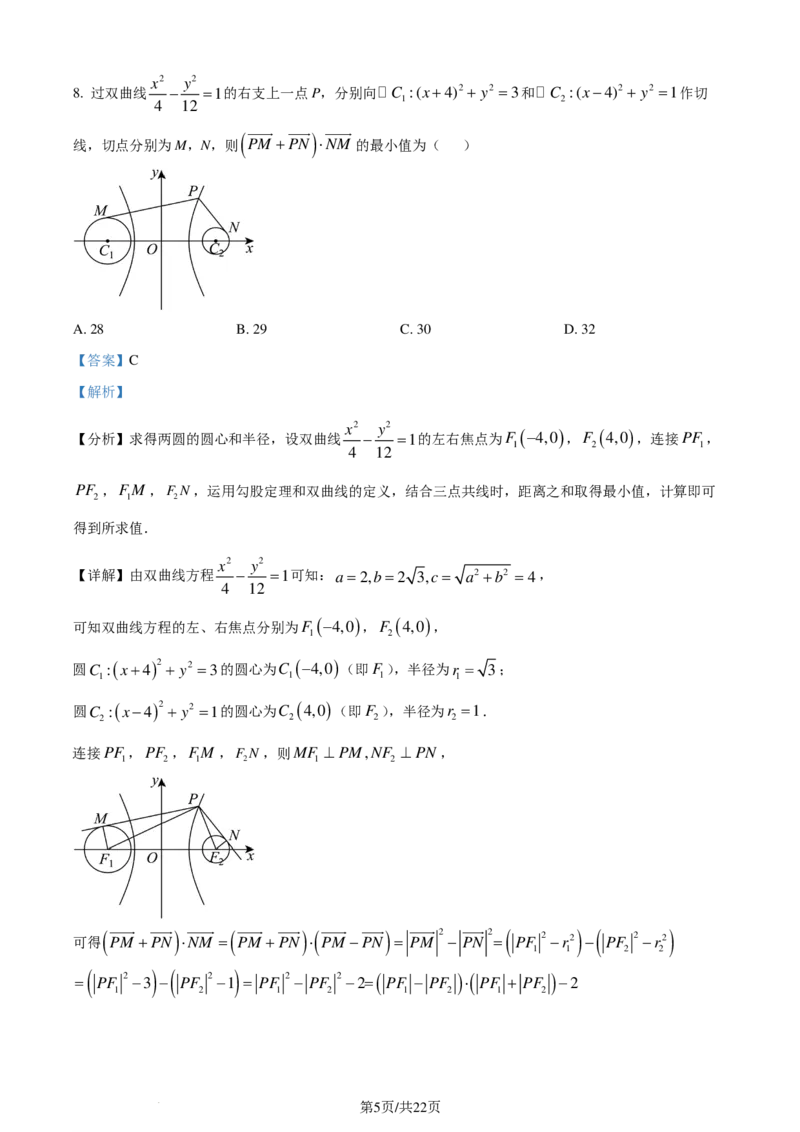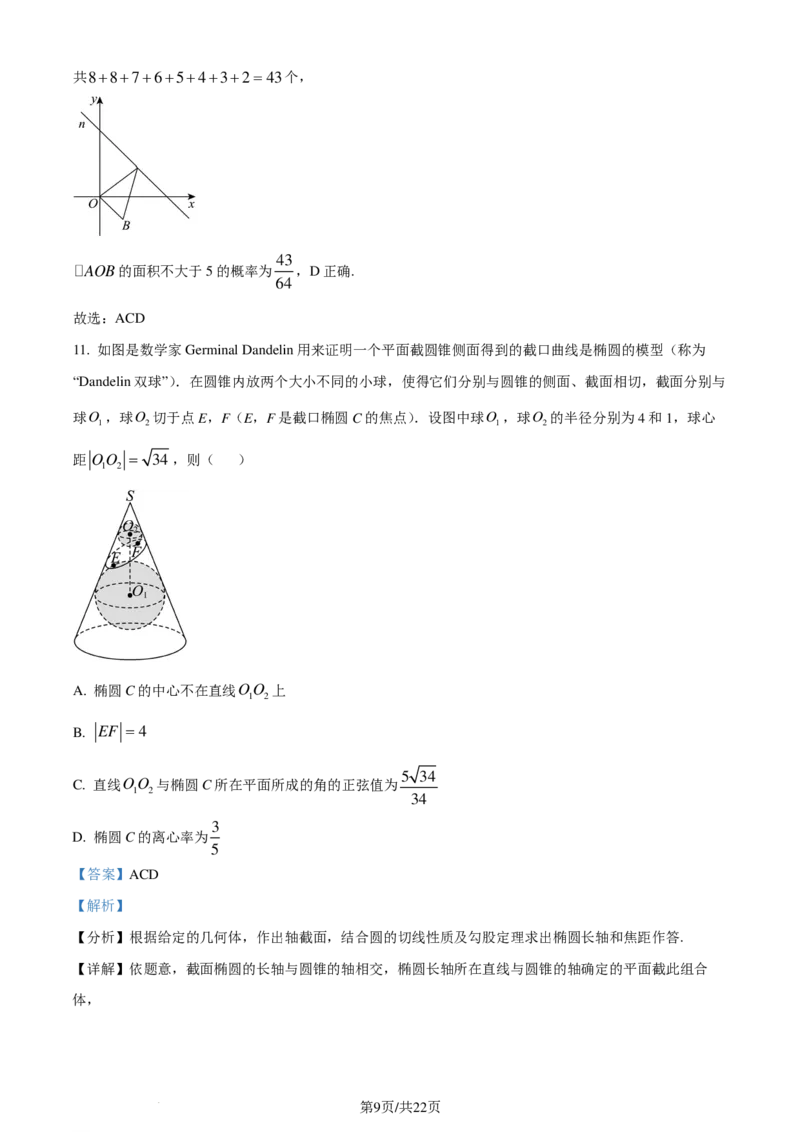1 2 2 3 3 1 【点睛】方法点睛：利用导数证明不等式的基本步骤 （1）作差或变形； ( ) （2）构造新的函数h x ； ( ) （3）利用导数研究h x 的单调性或最值； （4）根据单调性及最值，得到所证不等式． 特别地：当作差或变形构造的新函数不能利用导数求解时，一般转化为分别求左、右两端两个函数的最值问 题． x2 y2 1 19. 已知椭圆C: + =1(a >b>0)的左、右焦点分别为F ，F ，离心率为 经过点F 且倾斜角为 a2 b2 1 2 2 1  π θ 0<θ< 的直线l与椭圆交于A，B两点（其中点A在x轴上方），且△ABF 的周长为8．将平面  2 2 xOy沿x轴向上折叠，使二面角A−FF −B为直二面角，如图所示，折叠后A，B在新图形中对应点记 1 2 为A′，B′． π （1）当θ= 时， 3 ①求证：A′O⊥ B′F ； 2 ②求平面A'FF 和平面A'B'F 所成角的余弦值； 1 2 2  π 15 （2）是否存在θ 0<θ< ，使得折叠后A′B′F 的周长为 ？若存在，求tanθ的值；若不存在，请  2 2 2 说明理由． 13 205 【答案】（1）①证明过程见解析；② 205 第18页/共22页 学科网（北京）股份有限公司3 35 （2） ，理由见解析 14 【解析】 【分析】（1）①根据椭圆定义得到4a=8，结合离心率得到c=1，求出b2 =a2 −c2 =3，得到椭圆方程， ( )  8 3 3 联立直线方程和椭圆，得到A 0, 3 ,B− ,− ，得到A′O⊥FF ，结合二面角A−FF −B为直   5 5   1 2 1 2 二面角，得到线面垂直，证明出结论； ②建立空间直角坐标系，求出两平面的法向量，从而求出面面角的余弦值； （2）设折叠前A ( x ,y ) ,B ( x ,y ) ，折叠后对应的A′( x ,y ,0 ) ,B′( x ,0,−y ) ，设出直线l的方程，与椭 1 1 2 2 1 1 2 2 1 圆方程联立，得到两根之和，两根之积，根据折叠前后的周长关系得到 AB − A′B′ = ，变形得到 2 1 28 −2y y = m2 +1 ( y + y )2 −4y y ，代入两根之和，两根之积，求出m2 = ，进而求出tanθ的值. 4 1 2 1 2 1 2 45 【小问1详解】 ①由椭圆定义可知 AF + AF =2a, BF + BF =2a， 1 2 1 2 所以△ABF 的周长L=4a =8，所以a=2， 2 c 1 因为离心率为 1 ，故 = ，解得c=1， 2 a 2 则b2 =a2 −c2 =3，由题意，椭圆的焦点在x轴上， x2 y2 所以椭圆方程为 + =1， 4 3 π 直线l: y−0=tan ⋅( x+1 )，即l: y = 3 ( x+1 )， 3 x2 y2 8 联立 + =1得15x2 +24x=0，解得x=0或− ， 4 3 5 8  8  3 3 当x=0时，y = 3×( 0+1 )= 3，当x=− 时，y = 3×  − +1 =− ， 5  5  5 ( )  8 3 3 因为点A在x轴上方，所以A 0, 3 ,B− ,− ，   5 5   故AO⊥FF ，折叠后有A′O⊥FF ， 1 2 1 2 因为二面角A−FF −B为直二面角，即平面A′FF ⊥FF B′，交线为FF ， 1 2 1 2 1 2 1 2 第19页/共22页 学科网（北京）股份有限公司A′O⊂平面A′FF ， 1 2 所以A′O⊥平面FF B′， 1 2 因为F B′⊂平面FF B′，所以A′O⊥F B′； 2 1 2 2 ②以O为坐标原点，折叠后的y轴负半轴为x轴，原x轴为y轴，原y轴正半轴为z轴，建立空间直角坐 标系， ( ) 3 3 8  则F ( 0,−1,0 ) ,A′ 0,0, 3 ,B′ ,− ,0,F ( 0,1,0 ) ， 1   5 5   2  ( )   3 3 13  A′F = 0,1,− 3 ,B′F =− , ,0， 2 2   5 5    其中平面A′FF 的法向量为n =( 1,0,0 )， 1 2 1  设平面A′B′F 的法向量为n =( x,y,z )， 2 2    n ⋅A′F =( x,y,z )⋅ ( 0,1,− 3 ) = y− 3z =0  2 2  则   3 3 13  3 3 13 ， n ⋅B′F =( x,y,z )⋅− , ,0=− x+ y =0  2 2   5 5   5 5  13 13  令y = 3得x= ,z =1，故n =  , 3,1， 3 2  3  设平面A′B′F 与平面A′FF 的夹角为ϕ， 2 1 2   n  ⋅n  ( 1,0,0 )⋅   13 , 3,1   1 2  3  13 205 则cosϕ= cosn ,n =   = = ， 1 2 n ⋅ n 169 205 1 2 +3+1 9 13 205 故平面A′B′F 与平面A′FF 的夹角的余弦值为 ； 2 1 2 205 【小问2详解】 第20页/共22页 学科网（北京）股份有限公司设折叠前A ( x ,y ) ,B ( x ,y ) ，折叠后对应的A′( x ,y ,0 ) ,B′( x ,0,−y ) ， 1 1 2 2 1 1 2 2 设直线l方程为my = x+1， x2 y2 ( ) 将直线l与椭圆方程 + =1联立得， 3m2 +4 y2 −6my−9=0， 4 3 6m −9 则 y + y = ,y y = ， 1 2 3m2 +4 1 2 3m2 +4 在折叠前可知 AB = ( x −x )2 +( y − y )2 ， 1 2 1 2 折叠后，在空间直角坐标系中， A′B′ = ( x −x )2 + y2 + y2 ，， 1 2 1 2 15 由 A′F + B′F + A′B′ = ， AF + BF + AB =8， 2 2 2 2 2 1 故 AB − A′B′ = ， 2 1 所以 AB − A′B′ = ( x −x )2 +( y − y )2 − ( x −x )2 + y2 + y2 = ①， 1 2 1 2 1 2 1 2 2 −2y y 1 1 2 = 分子有理化得 ， ( x −x )2 +( y − y )2 + ( x −x )2 + y2 + y2 2 1 2 1 2 1 2 1 2 所以 ( x −x )2 +( y − y )2 + ( x −x )2 + y2 + y2 =−4y y ②， 1 2 1 2 1 2 1 2 1 2 1 由①②得 ( x −x )2 +( y − y )2 = −2y y ， 1 2 1 2 4 1 2 因为 ( x −x )2 +( y − y )2 = ( my −1−my +1 )2 +( y − y )2 1 2 1 2 1 2 1 2 = m2 +1 y − y ， 1 2 1 故 −2y y = m2 +1 y − y ， 4 1 2 1 2 1 即 −2y y = m2 +1 ( y + y )2 −4y y ， 4 1 2 1 2 1 2 6m −9 将 y + y = ,y y = 代入上式得 1 2 3m2 +4 1 2 3m2 +4 2 1 18  6m  36 + = m2 +1   + ， 4 3m2 +4 3m2 +4 3m2 +4 两边平方后，整理得2295m4 +4152m2 −3472=0， ( )( ) 28 即 45m2 −28 51m2 +124 =0，解得m2 = ， 45 π 1 3 35 因为0<θ< ，所以tanθ= = . 2 m 14 第21页/共22页 学科网（北京）股份有限公司【点睛】出题非常新颖，将立体几何和解析几何结合，考查学生的综合能力，在解决图形的翻折问题时， 应找出其中变化的量和没有变化的量，包括位置关系和数量关系，通常翻折后还在同一平面上的元素之间 的位置关系不发生变化，不在同一平面上的元素之间的位置关系发生变化，解题时应抓住不变量，利用平 面几何知识或建立空间直角坐标系进行求解. 第22页/共22页 学科网（北京）股份有限公司