文档内容
湖南省 2024 届高三九校联盟第二次联考
数学
由 长沙市一中 常德市一中 湖南师大附中 双峰县一中 桑植县一中
武冈市一中 湘潭市一中 岳阳市一中 株洲市二中 联合命题
炎德文化审校、制作
命题学校:长沙市一中 审题学校:双峰县一中
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无
效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的)
1.对两个变量 和 进行回归分析,得到一组样本数据 ,下列统计量的数值能
够刻画其经验回归方程的拟合效果的是( )
A.平均数 B.相关系数 C.决定系数 D.方差
2.已知 是等比数列, 是其前 项和.若 ,则 的值为( )
A.2 B.4 C. D.
3.关于复数 与其共轭复数 ,下列结论正确的是( )
A.在复平面内,表示复数 和 的点关于虚轴对称
B.
C. 必为实数, 必为纯虚数
D.若复数 为实系数一元二次方程 的一根,则 也必是该方程的根
4.已知 为双曲线 上一动点,则 到点 和到直线 的距离之比为( )
A.1 B. C. D.2
5.如图,在四面体 中, 平面 ,则此四面体的外接球表
面积为( )A. B. C. D.
6.某银行在2024年初给出的大额存款的年利率为3%,某人存入大额存款 元,按照复利计算10年后得到的
本利和为 ,下列各数中与 最接近的是( )
A.1.31 B.1.32 C.1.33 D.1.34
7.已知函数 ,若沿 轴方向平移 的图象,总能保证平移后的曲线与直线
在区间 上至少有2个交点,至多有3个交点,则正实数 的取值范围为( )
A. B. C. D.
8.过点 的动直线与圆 交于 两点,在线段 上取一点 ,使
得 ,已知线段 的最小值为 ,则 的值为( )
A.1 B.2 C.3 D.4
二、多选题(本大题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列函数的图象与直线 相切的有( )
A. B.
C. D.
10.在 中,角 所对的边分别为 ,且 ,则下列结论正确的有( )
A.
B.若 ,则 为直角三角形C.若 为锐角三角形, 的最小值为1
D.若 为锐角三角形,则 的取值范围为
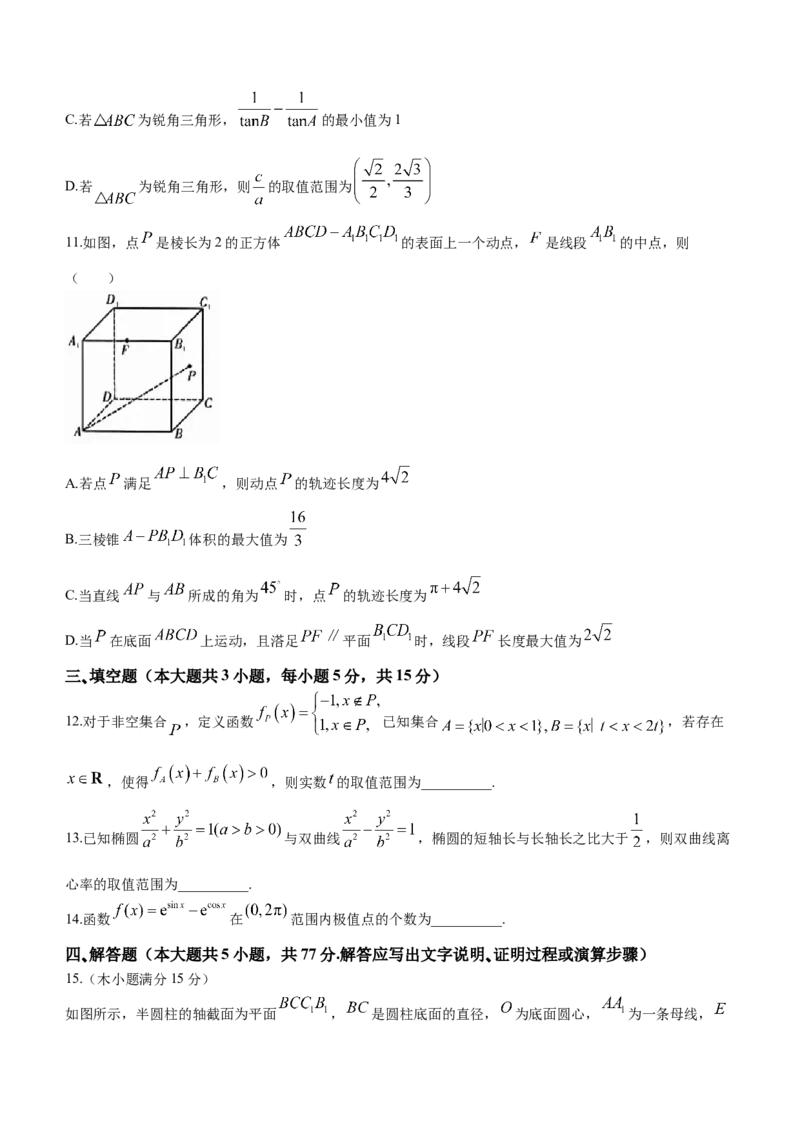
11.如图,点 是棱长为2的正方体 的表面上一个动点, 是线段 的中点,则
( )
A.若点 满足 ,则动点 的轨迹长度为
B.三棱锥 体积的最大值为
C.当直线 与 所成的角为 时,点 的轨迹长度为
D.当 在底面 上运动,且溚足 平面 时,线段 长度最大值为
三、填空题(本大题共3小题,每小题5分,共15分)
12.对于非空集合 ,定义函数 已知集合 ,若存在
,使得 ,则实数 的取值范围为__________.
13.已知椭圆 与双曲线 ,椭圆的短轴长与长轴长之比大于 ,则双曲线离
心率的取值范围为__________.
14.函数 在 范围内极值点的个数为__________.
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(木小题满分15分)
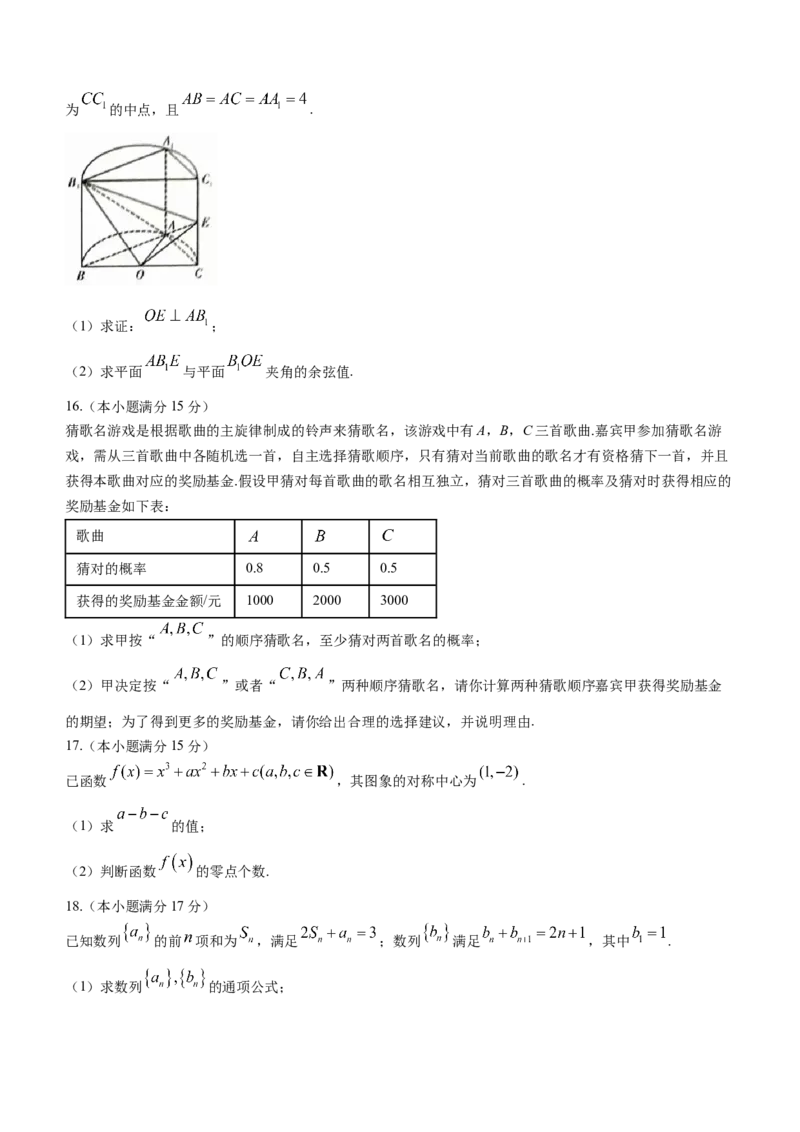
如图所示,半圆柱的轴截面为平面 , 是圆柱底面的直径, 为底面圆心, 为一条母线,为 的中点,且 .
(1)求证: ;
(2)求平面 与平面 夹角的余弦值.
16.(本小题满分15分)
猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名,该游戏中有A,B,C三首歌曲.嘉宾甲参加猜歌名游
戏,需从三首歌曲中各随机选一首,自主选择猜歌顺序,只有猜对当前歌曲的歌名才有资格猜下一首,并且
获得本歌曲对应的奖励基金.假设甲猜对每首歌曲的歌名相互独立,猜对三首歌曲的概率及猜对时获得相应的
奖励基金如下表:
歌曲
猜对的概率 0.8 0.5 0.5
获得的奖励基金金额/元 1000 2000 3000
(1)求甲按“ ”的顺序猜歌名,至少猜对两首歌名的概率;
(2)甲决定按“ ”或者“ ”两种顺序猜歌名,请你计算两种猜歌顺序嘉宾甲获得奖励基金
的期望;为了得到更多的奖励基金,请你给出合理的选择建议,并说明理由.
17.(本小题满分15分)
已函数 ,其图象的对称中心为 .
(1)求 的值;
(2)判断函数 的零点个数.
18.(本小题满分17分)
已知数列 的前 项和为 ,满足 ;数列 满足 ,其中 .
(1)求数列 的通项公式;(2)对于给定的正整数 ,在 和 之间插入 个数 ,使 ,
成等差数列.
(i)求 ;
(ii)是否存在正整数 ,使得 恰好是数列 或 中的项?若存在,求出所有满足条
件的 的值;若不存在,说明理由.
19.(本小题满分17分)
直线族是指具有某种共同性质的直线的全体,例如 表示过点 的直线,直线的包络曲线定义为:
直线族中的每一条直线都是该曲线上某点处的切线,且该曲线上的每一点处的切线都是该直线族中的某条直
线.
(1)若圆 是直线族 的包络曲线,求 满足的关系式;
(2)若点 不在线族: 的任意一条直线上,求 的取值范
和直线族 的包络曲线 ;
(3)在(2)的条件下,过曲线 上 两点作曲线 的切线 ,其交点为 .已知点 ,若
三点不共线,探究 是否成立?请说明理由.湖南省 2024 届高三九校联盟第二次联考
数学参考答案
命题学校:长沙市一中 审题学校:双峰县一中
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的每个这项中,只有一项
是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案 C C D C B D A A
1.C 【解析】平均致与方差是用来反馈数据集中趋势与波动程度大小的就计量:变量y和x之间的相关系
数”的绝对值总大,则变量y和x之间线性相关关系越强;用决定系数R来刻画回归效果,R越大说明拟合效
果总好:综上选C
2.C 【解析】 ,化简得 ,整理得 ,又
, .故选C.
3.D 【解析】对于选项A,表示复数 和 的点关于实轴对称,故错误:对于选项B、选项C,当 时均
不成立,故错误.故选D
4.C 【解析】取双曲线上一点 ,则 ,故选C.
5.B 【解析】将四面体 补形成长方体,长、宽、高分别为 ,外接球直径等于体对角线长故
,所以外接球表面积为 .故选 .
6.D 【解析】存入大额存款 元,按照复利计算,可得每年末本利和是以为 首项, 为公比的等比
数列,,所认 ,可得
,故选D.7.A 【解析】由题知, ,若沿 轴方向平移,考点其任意性,不妨设得到的函数
,令 ,即 ,由正弦曲线性质知, 至少有2解,至
多有3解,则自变量 的区间长度在 到 之间,耶 ,那 ,选A.
8.A 【解析】圆心 ,半径为2,所以圆与 解相切,设切点为 .则 ,连接 ,则
,则 .
设 的中点为 ,连接 ,则 ,
语圆心 列直线 的距离为 ,则 .
由 可得 ,
因为 .所以 .
因此 ,解得: ,故选A.
二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
题号 9 10 11
答案 AC ABD CD
9.AC 【解析】选项A中, 与 相切于点 ;选项B中, 与 没有交点;选项C中, 与 相切于点 ;选项D中, 与 有三个交点,
, ,均不是切点.
10.ABD 【解析】对于 中,由正弦定理得 ,由 ,得
.即 ,由 ,则 ,故 ,所
以 或 ,即 或 (舍去),即 正确:
对于 ,结合 和正弦定理知 ,又 ,数
,B正确;
对于 ,在锐角 中, ,即 .
故 ,C错误;
对于 ,在锐角 中,由 .
由对勾函数性质知, ,D正确;故选ABD.
11.CD 【解析】对 ,易知 平面 平面 ,故动点 的轨迹为矩形 ,动
点 的轨迹长度为 ,所认 错误;
对 因为 ,而 的面积为定值 ,要使三棱锥 的体积最大,当且仅当
点 到平面 距离最大,易知,点 是正方体意向到平面 距离最大的点,
错误;对C:连接AC, ,以B为圆心, 为半径画弧 ,如图1所示,
当点 在线段 和弧 上时,直线 与 所成的角为 ,
又 ,
弧 长度 ,故点 的轨迹长度为 ,故 正确;
对D;取 的中点分别为 ,
连接 ,如图2所示,
因为 面 面 ,故 面 ,
, 面 面 ,故 面 ;
又 面 ,故平面 面 ;
又 ,故平面 与平面 是同一个平面.
则点 的轨迹为线段 :
在三角形 中,
则 ,故三角形 是以 为直角的直角三角形;
故 ,故 长度的最大值为 ,故 正确.故选: .三、填空题(本大题共3小题,年小题5分,共15分)
12. 【解析】由题知: 可取 ,若 .则 ,即
集合 ,得 ,郎 的取值范围为 .
13. 【解析】因为 .
14.2 【解析】 .
当 时, ;当 时, ;
当 时, 和 均为单调减函数,又 在 上是单调增函数,根据复合
函数单调性可知 为减函数 ,又 ,故函数
在该区间上存在一个零点,该零点为函数 的极值点;
从而函数 在 内一共有2个极值点.
四、解答题(本大题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤)
15.【解析】(1)由 是直径可知 ,则 是是等腰直角三角形,故 ,
由圆柱的特征可知 平面 ,又 平面 ,所以 ,
因为 平面 ,则 平面 ,
而 平面 ,则 ,因为 ,则 ,
,
所以 ,
因为 平面 ,
所以 平面 ,又 平面 ,故 .
(2)由题意及(1)易知 两两垂直,如图所示建立空间直角坐标系,
则 ,所以
,
由(1)知 平面 ,故平面 的一个法向量是
设 是平面 的一个法向量,
则有 取 ,所以
设平面 与平面 夹角为 ,
所以 ,
则平面 与平面 夹角的余弦值为 .
16.【解析】1)设“甲按‘A,B,C’的顺序猜歌名至少猜对两首歌名”为事件E,
则 ;则 的所有可能取值为 ,
所以 ;
则 的所有可能取值为 ,
所以 .
参考答案一:由于 ,
由于 ,所以应该安装“ ”的顺序猜歌名.
参考答案二:甲按“C,B,A”的顺序猜歌名时,获得0元的概率为0.5,大于按照“A,B,C”的顺序猜歌名
时获得0元的概率,所以应孩按照“A,B,C”的顺序猜歌名.
其他合理答案均给分,
17.【解析】(1)图为函教 的图象关于点 中心付称,故 为夺函数,
从而有 ,即 .
,
.所以 解得 故 ;
(2)法一:由(1)可知, ,
当 时, 为单调增函教, ,
,
函数 有且仅有一个零点;
当 时, 有两个正根 ,满足 ,且 ,
数 在区间 上单调递增,在区间 上单调递减,在区间 上单调递增,
,
函数 有且仅有一个零点;
当 时, 有两个零点
当 时, 有两个根 ,满足 ,
函数 在区间 上单调递增,在区间 上单调递减,在区间 上单调递增,
函致 有且仅有三个零点;
综上,当 时,函数 有三个零点;当 时,函数 有两个零点;当 时,函数 有
一个零点
法二:由(1)可知, ,今 ,则
可以转化为 与 两个这数图象交点的个数,今 ,则 ,
故 在区间 上单调递减,在区间 上单调递增在区间 上单调递增,
当 单调递增 时, 趁于 ;
当x趋于1且比1小时, 趋于+∞:当x趋于1且比1大时, 趋于 :
当 单调递增 时, 趋于 .
所以,当 时,有三个交点;当 时,有两个交点;当 时,有一个交点.
综上,当 时,函数 有三个零点;当 时,函数 有两个零点;当 时,函数 有
一个零点.
注意,如果是保留参数b,则答案为:
当 时,函数 有一个零点;当 时,函数 有两个零点;当 时,函数 有三个零
点.
18.【解析】(1)由 ①,当 时, ②,
①-②得 ,
当 时, ,
是首项为1,公比为 的等比数列,故 ,
由 ③.由得 ,又 ④.
④-③得 ,
的所有奇数项构成首项为1,公差为2的等差数列:所有偶数项构成首项为2,公差为2的等差数列.
得 .
综上: ;
(2)(i)在 和 之间新入 个数 ,使 成等差数列,
设公差为 ,则 ,
则 .
⑤
则 ⑥
⑤-⑥得: ,
(ii)由(1) ,又 ,
由已知 ,
假设 是数量列 或 中的一项,不妨设 ,
因为 ,所以 ,而 ,
所以 不可能是数列 中的项.
假设 是 中的项,则 .
当 时,有 ,即 ,令 ,
当 时, ;当 时, ,由
知 无解.
当 时,有 ,即 .所以存在 使得 是数列 中的第3项.
故存在正整数 使得 是数列 中的第3项.
19.【解析】(1)由定义可知, 与 相切,则圆 的圆心 到直线 的
距离等于1,则 ,叔 .
(2)点 不在直线族 的任意一条直线上,所以无论 取何
值时, 无解.
将 整理成关于 的一元二次方程;
.若该方程无解,则 ,即 .
证明:在 上任取一点 在该点处的切线斜率为 ,于是可以得到 在
点处的切线方程为: ,即 .
今直线族 中 ,则直线为 ,
所以该曲线上的每一点处的切线都是该直线族中的某条直线,
而对任意 那是抛物线在点 处的切线.
所以直线族 的包络曲线 为 .
(3)法一:已知 ,设 ,则 .
.
由(2)知, 在点 处的切线方程为 ;同理 在点 处的切线方
程为 .
,所以 .
因此 ,
同理: .所以 ,
即 ,所以 成立.
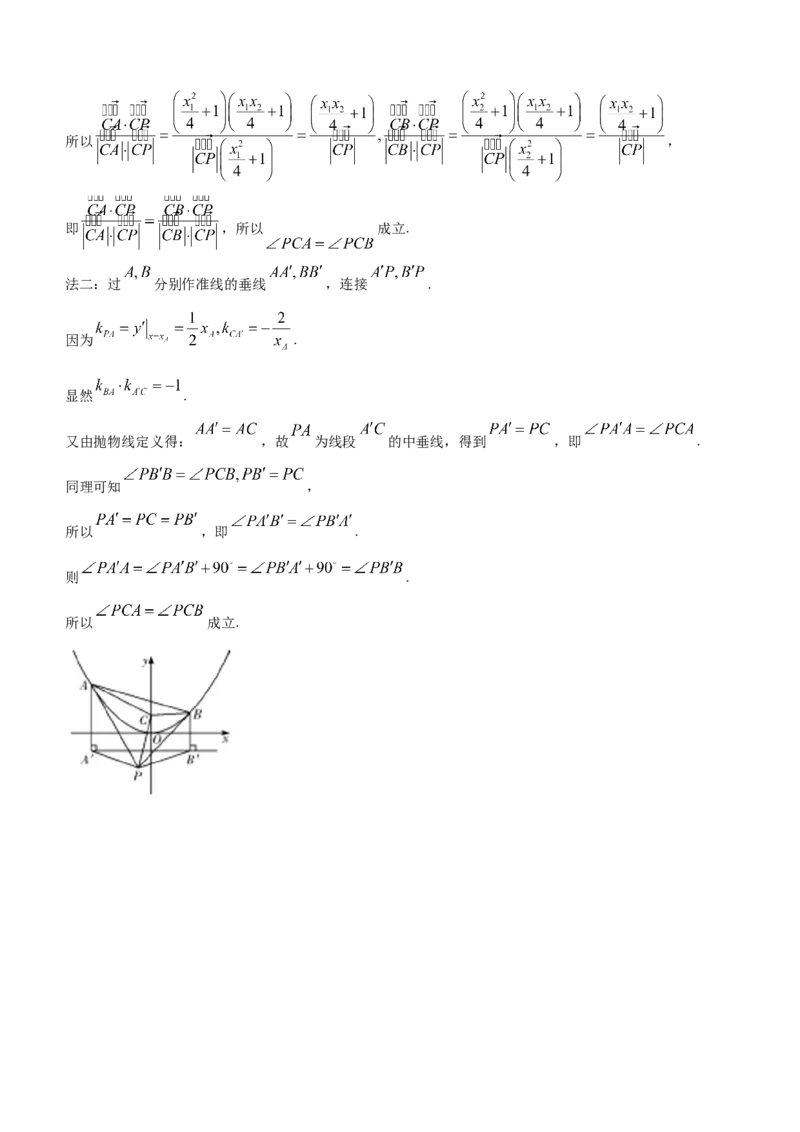
法二:过 分别作准线的垂线 ,连接 .
因为 .
显然 .
又由抛物线定义得: ,故 为线段 的中垂线,得到 ,即 .
同理可知 ,
所以 ,即 .
则 .
所以 成立.