文档内容
成都外国语学校 2025-2026 学年度上期十二月月考考试
高二数学试卷
命题人:方兰英 林琪琦 审题人:方兰英 金鑫 林琪琦
注意事项:
1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.本堂考试120分钟,满分150分;
3.答题前,考生务必先将自己的姓名、学号填写在答题卡上,并使用2B铅笔填涂.
4.考试结束后,将答题卡交回.
第I卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 直线 的倾斜角为( )
A. B. C. D.
2. 如图是一个古典概型的样本空间 和事件A、B,其中 , , ,
,那么( )
A. B. 事件A与B互斥
C. D. 事件A与B相互独立
3. 长轴长是短轴长的 倍,且经过点 的椭圆的标准方程为( )
A. B.C. 或 D. 或
4. 在三棱锥 中, 是 的中点,点 在棱 上,且 ,则 ( )
A. B.
C. D.
5. 2021年某省实施新的“ ”高考改革方案,“3”即为语文、数学、英语3科必选,“1”即为从物理和历
史中任选一科,“2”即为从化学、生物、地理、政治中任选2科,则该省某考生选择全理科(物理、化学、生物)
的概率是( )
A. B. C. D.
6. 圆 关于直线 对称的圆的标准方程为( )
A. B.
C. D.
7. 如图,把正方形纸片 沿对角线 折成 的二面角, , 分别为 , 的中点, 是
原正方形 的中心,则折纸后 的余弦值为( )
A. B. C. D.
8. 已知 是椭圆 和双曲线 的公共焦点,M是该椭圆和双曲线的一个公共点,, 的外接圆半径为2,且 ,记椭圆的离心率为 ,双曲线的离心率为
,则下列说法正确的是()
A. B.
C. D. 的最小值为
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
题目要求.
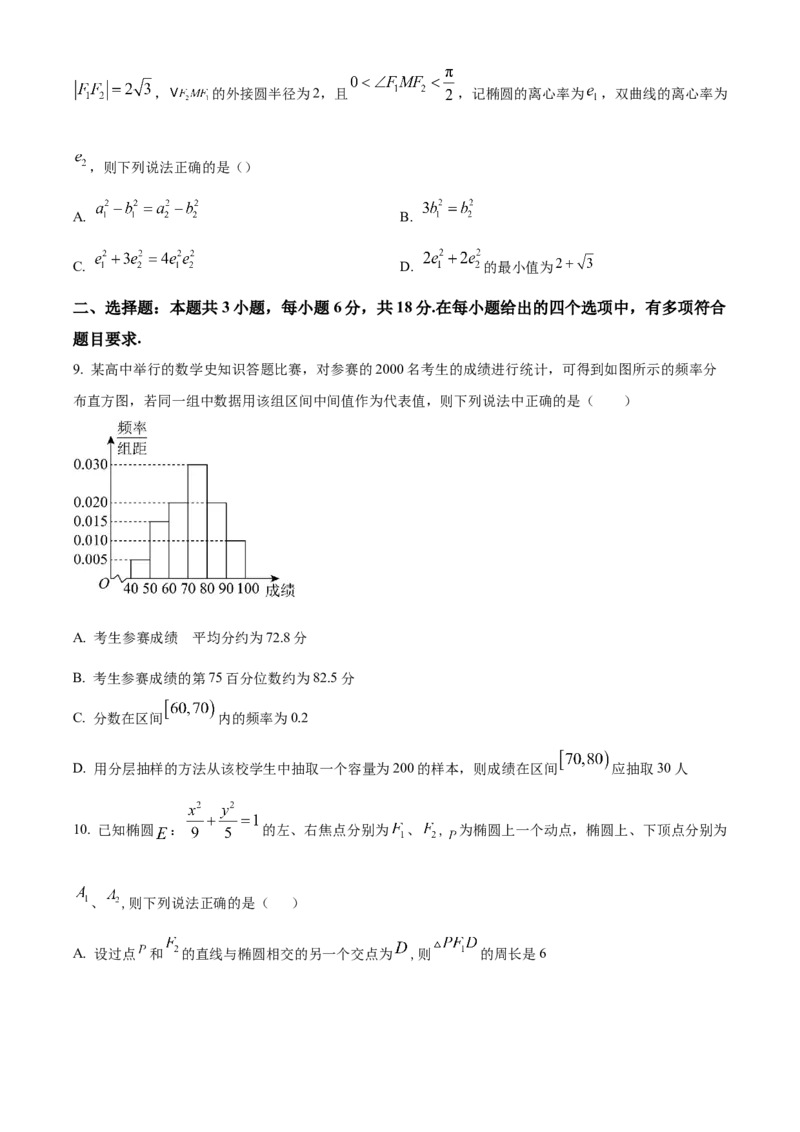
9. 某高中举行的数学史知识答题比赛,对参赛的2000名考生的成绩进行统计,可得到如图所示的频率分
布直方图,若同一组中数据用该组区间中间值作为代表值,则下列说法中正确的是( )
的
A. 考生参赛成绩 平均分约为72.8分
B. 考生参赛成绩的第75百分位数约为82.5分
C. 分数在区间 内的频率为0.2
D. 用分层抽样的方法从该校学生中抽取一个容量为200的样本,则成绩在区间 应抽取30人
10. 已知椭圆 : 的左、右焦点分别为 、 , 为椭圆上一个动点,椭圆上、下顶点分别为
、 ,则下列说法正确的是( )
A. 设过点 和 的直线与椭圆相交的另一个交点为 ,则 的周长是6B. 若 ,则 的面积为
C.
D. 若 为圆 : 上的一个动点,则 的最大值为12
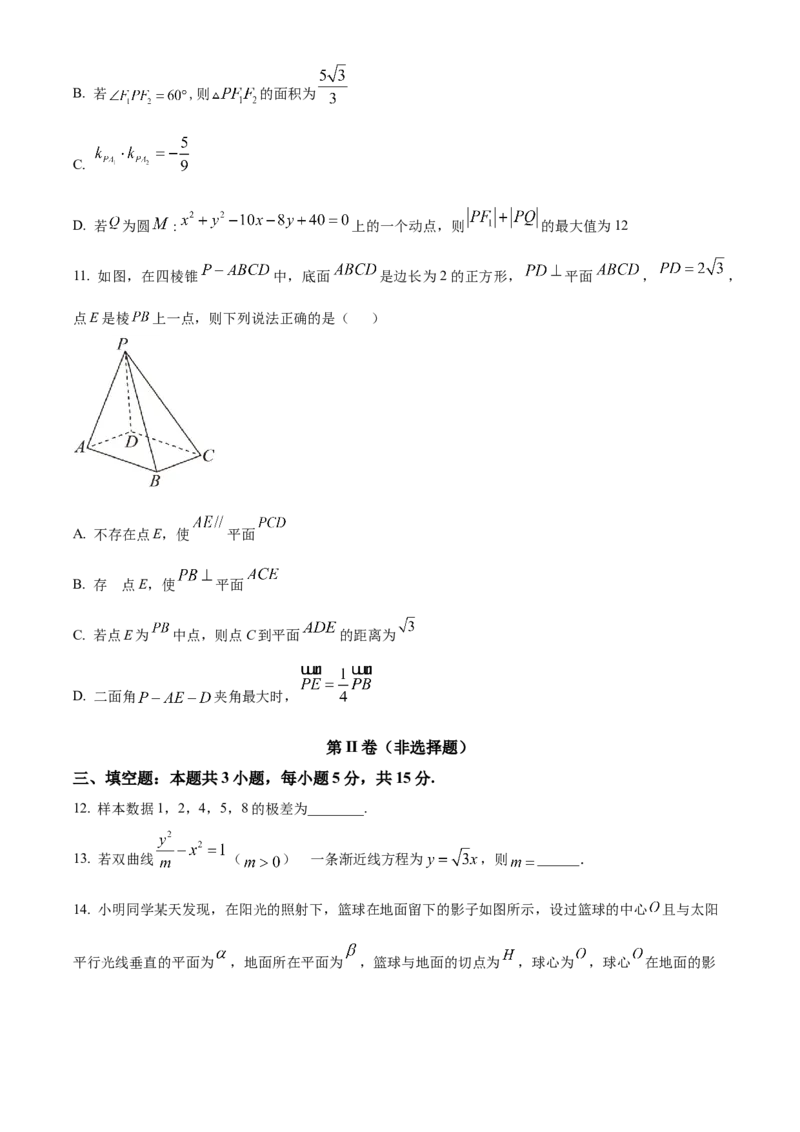
11. 如图,在四棱锥 中,底面 是边长为2的正方形, 平面 , ,
点E是棱 上一点,则下列说法正确的是( )
A. 不存在点E,使 平面
在
B. 存 点E,使 平面
C. 若点E为 中点,则点C到平面 的距离为
D. 二面角 夹角最大时,
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分.
12. 样本数据1,2,4,5,8的极差为________.
13. 若双曲线 ( ) 一的条渐近线方程为 ,则 ______.
14. 小明同学某天发现,在阳光的照射下,篮球在地面留下的影子如图所示,设过篮球的中心 且与太阳
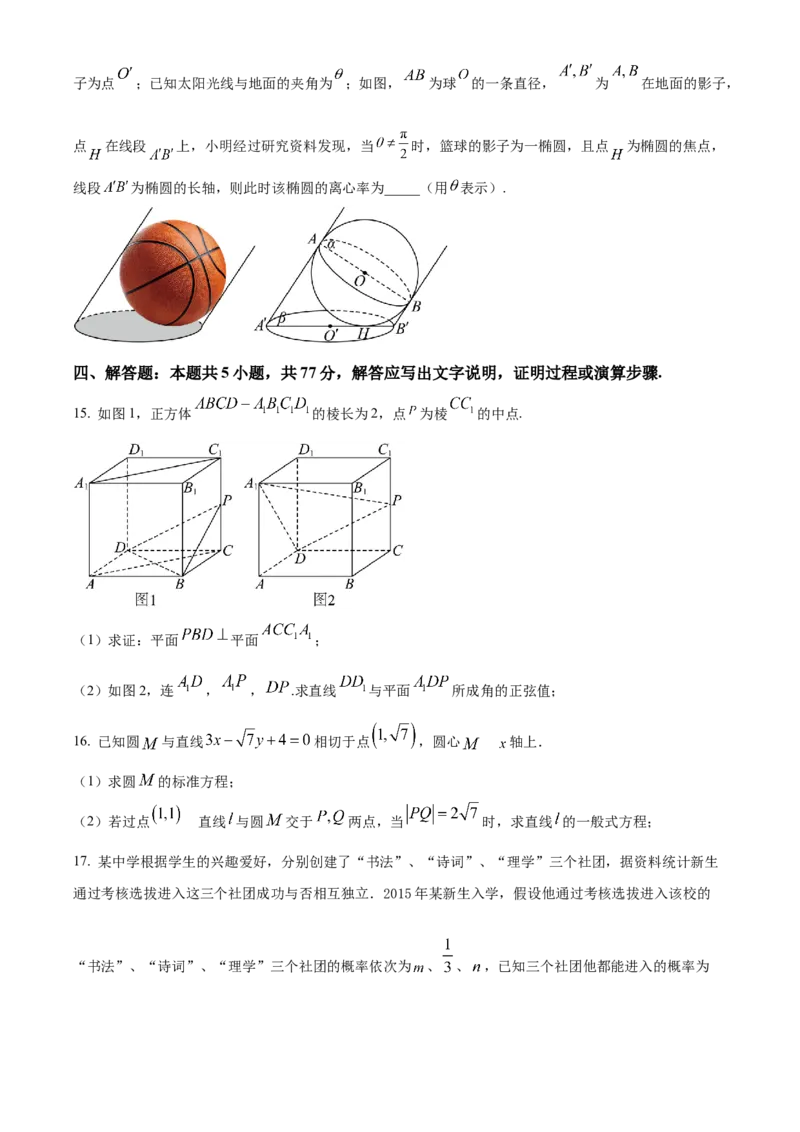
平行光线垂直的平面为 ,地面所在平面为 ,篮球与地面的切点为 ,球心为 ,球心 在地面的影子为点 ;已知太阳光线与地面的夹角为 ;如图, 为球 的一条直径, 为 在地面的影子,
点 在线段 上,小明经过研究资料发现,当 时,篮球的影子为一椭圆,且点 为椭圆的焦点,
线段 为椭圆的长轴,则此时该椭圆的离心率为_____(用 表示).
四、解答题:本题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤.
15. 如图1,正方体 的棱长为2,点 为棱 的中点.
(1)求证:平面 平面 ;
(2)如图2,连 , , .求直线 与平面 所成角的正弦值;
16. 已知圆 与直线 相切于点 ,圆心 在轴上.
(1)求圆 的标准方程;
(2)若过点 直的线 与圆 交于 两点,当 时,求直线 的一般式方程;
17. 某中学根据学生的兴趣爱好,分别创建了“书法”、“诗词”、“理学”三个社团,据资料统计新生
通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学,假设他通过考核选拔进入该校的
“书法”、“诗词”、“理学”三个社团的概率依次为 、 、 ,已知三个社团他都能进入的概率为,至少进入一个社团的概率为 ,且 .
(1)求 与 的值;
(2)该校根据三个社团活动安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”
社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方
面获得校本选修课学分分数不低于4分的概率.
18. 已知圆 和圆 ,动圆 与圆 、圆 都外切或都内切,记点
的轨迹为曲线 .
(1)求曲线 的方程;
(2)若过点 的直线 与曲线 的两个交点 分别在 轴两侧.
①求直线 斜率的取值范围;
②若 是点 关于 轴的对称点,证明:直线 过定点,并求出该定点.
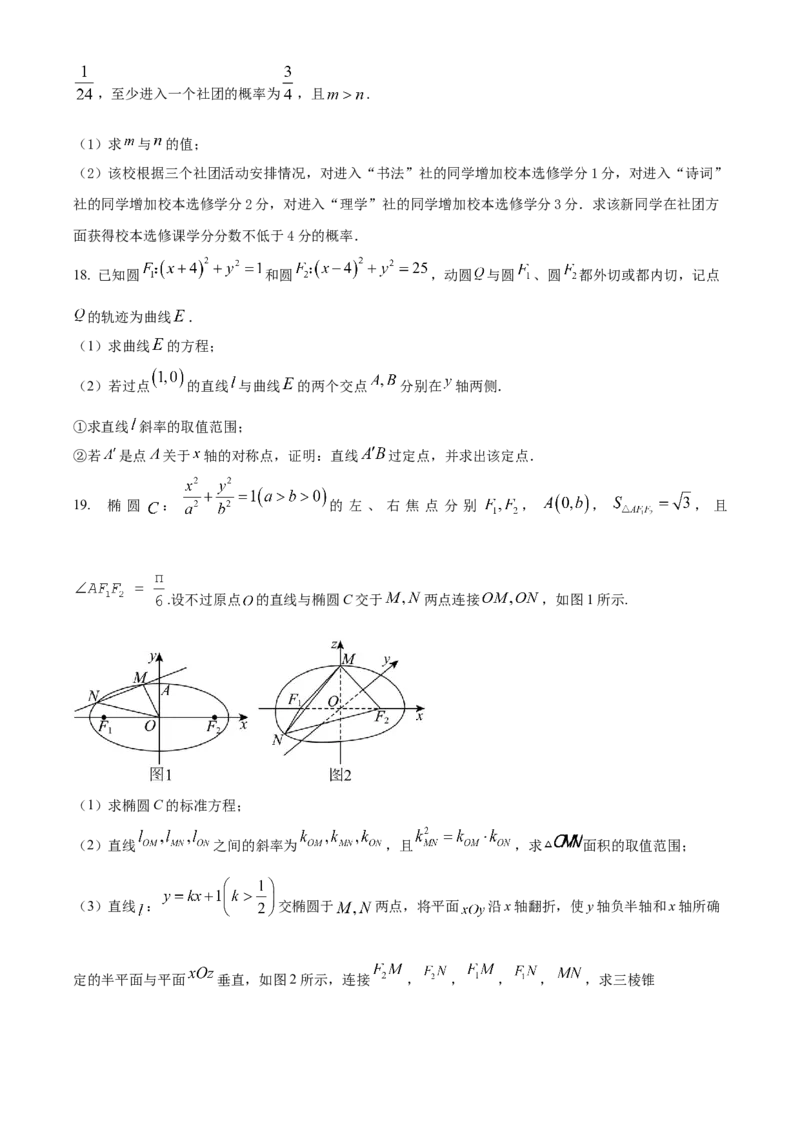
19. 椭 圆 : 的 左 、 右 焦 点 分 别 , , , 且
.设不过原点 的直线与椭圆C交于 两点连接 ,如图1所示.
(1)求椭圆C的标准方程;
(2)直线 之间的斜率为 ,且 ,求 面积的取值范围;
(3)直线 : 交椭圆于 两点,将平面 沿x轴翻折,使y轴负半轴和x轴所确
定的半平面与平面 垂直,如图2所示,连接 , , , , ,求三棱锥外接球表面积的最小值.