专题06染色问题_2024-2025高三（6-6月题库）_2024年08月试卷_0816新高考数学题型全归纳之排列组合（20个专题）

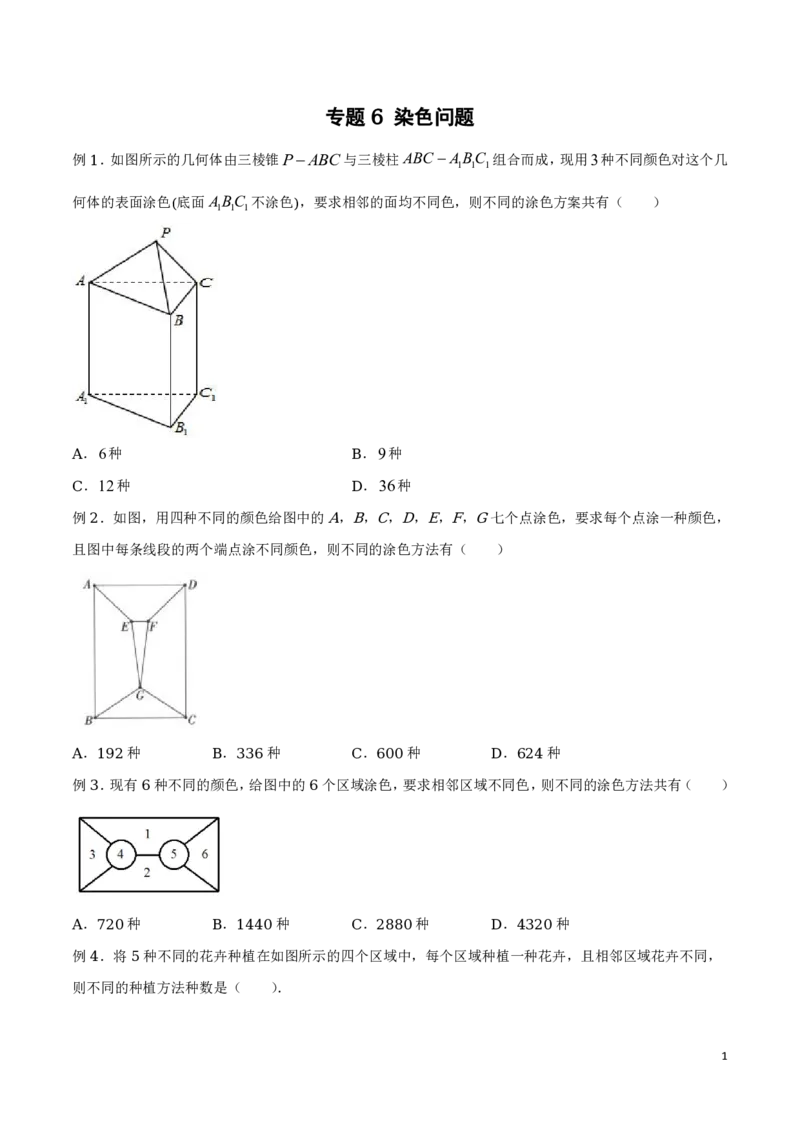
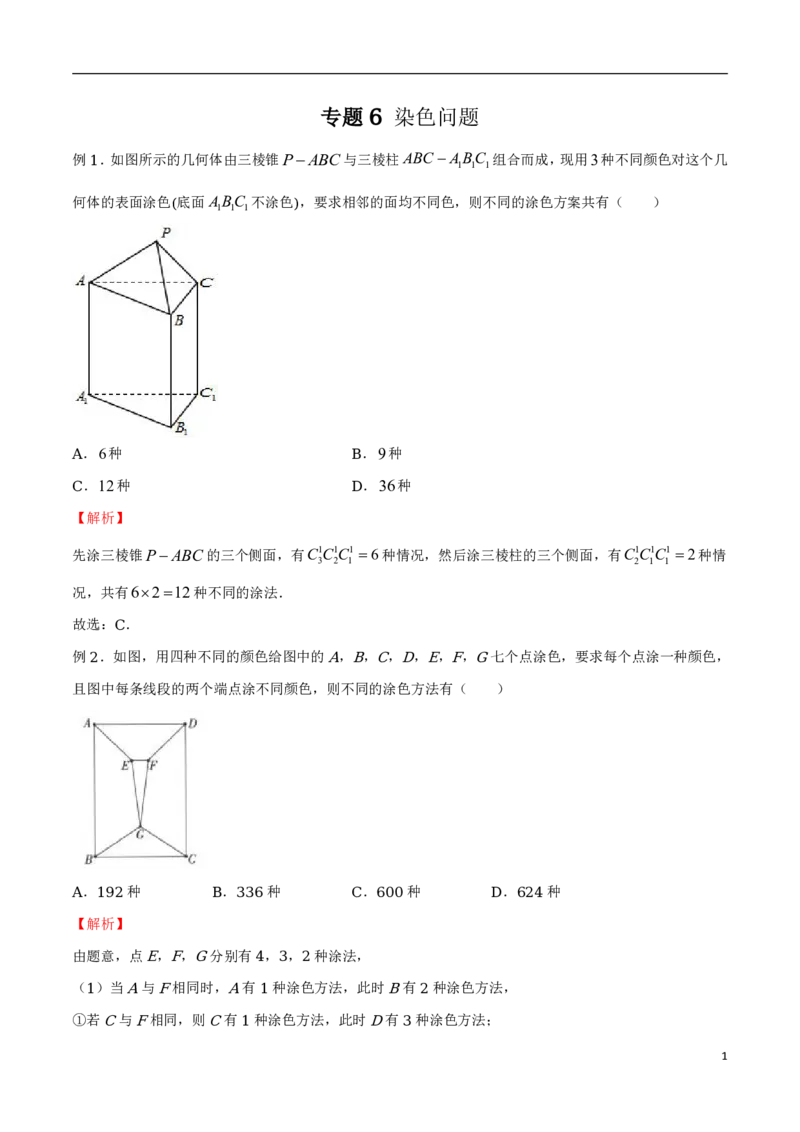
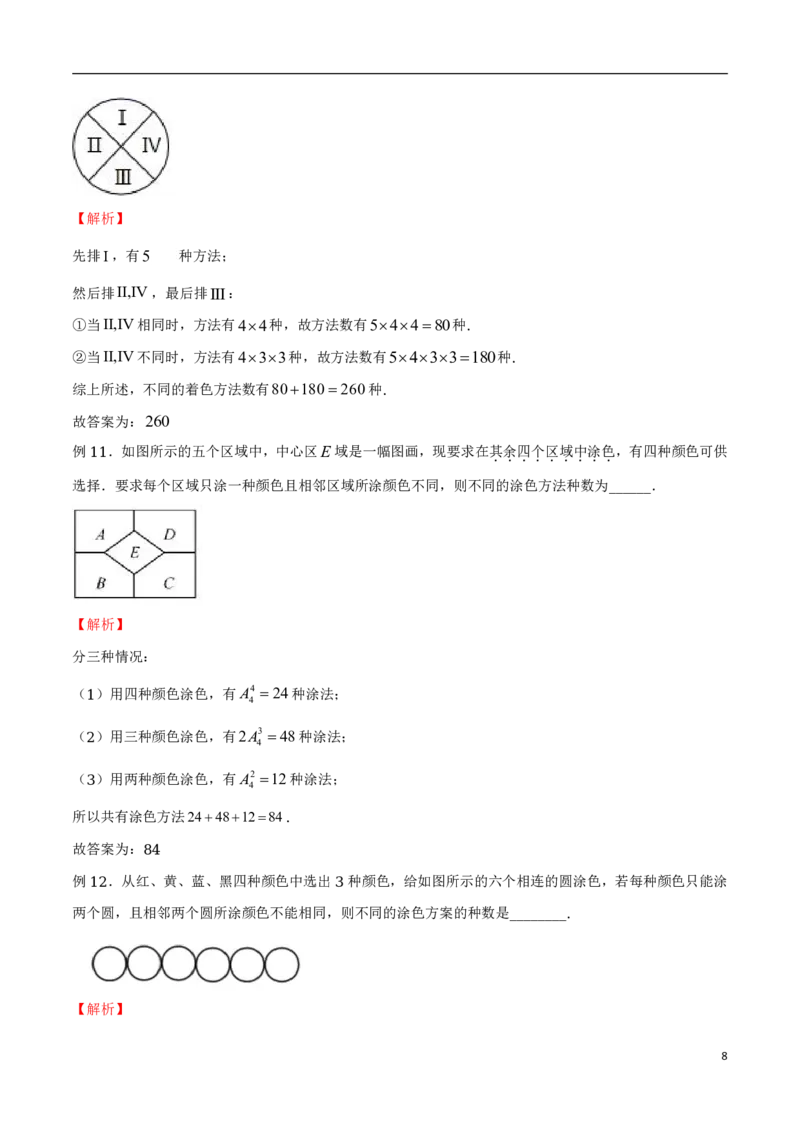
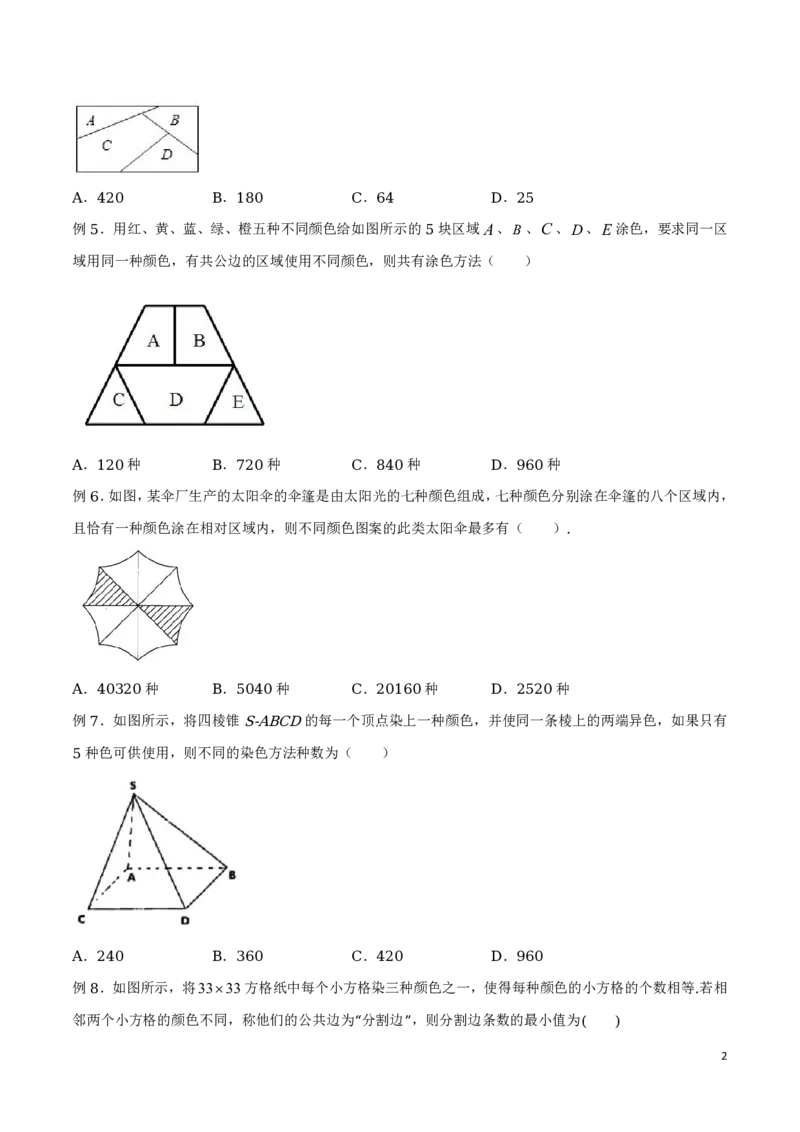
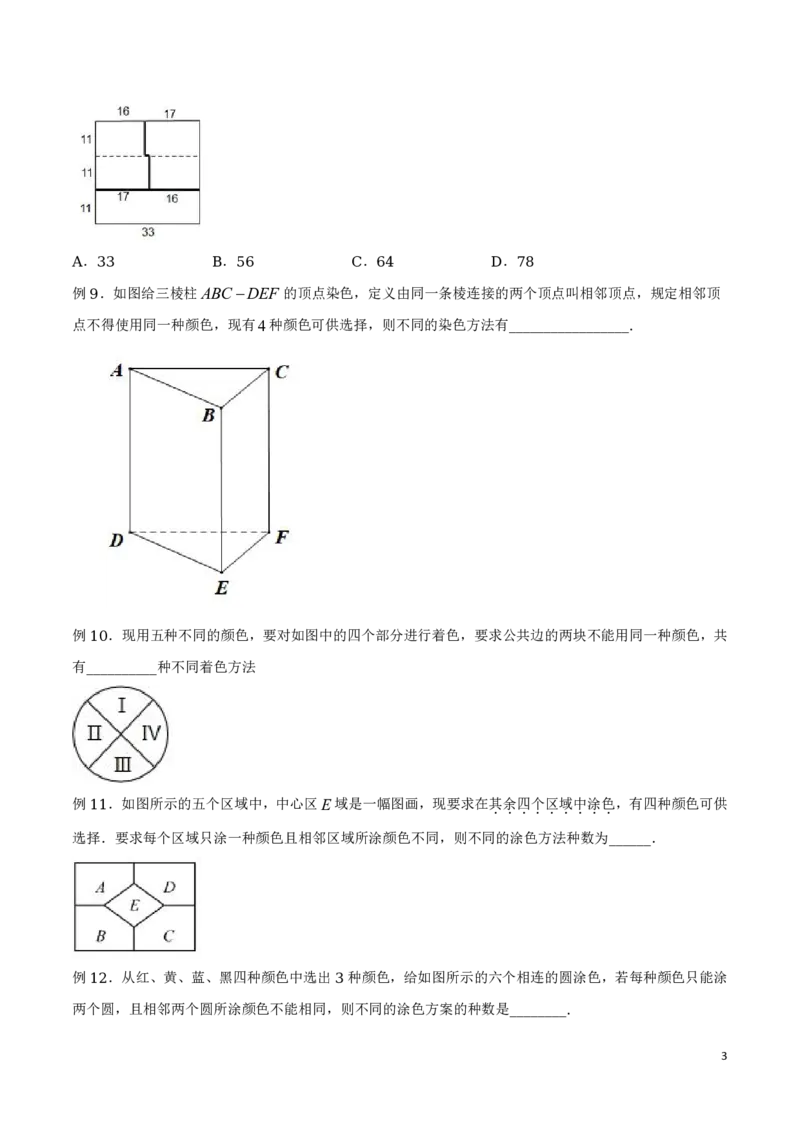
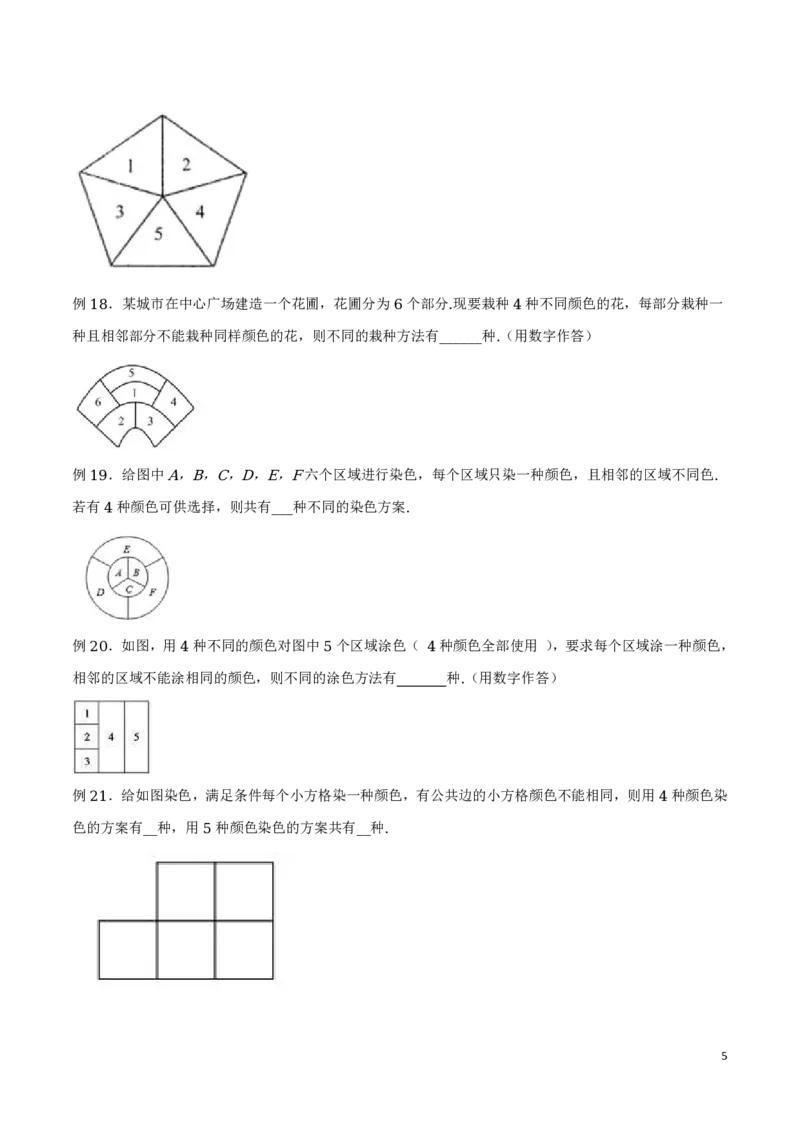
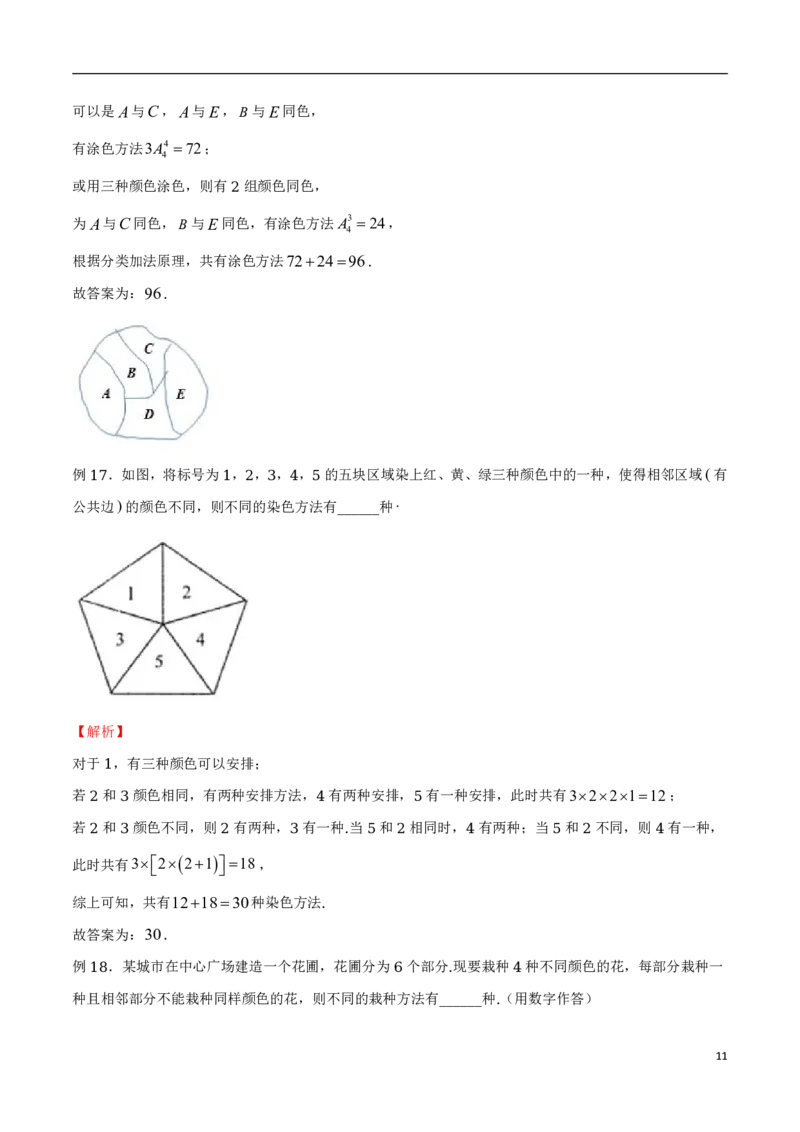
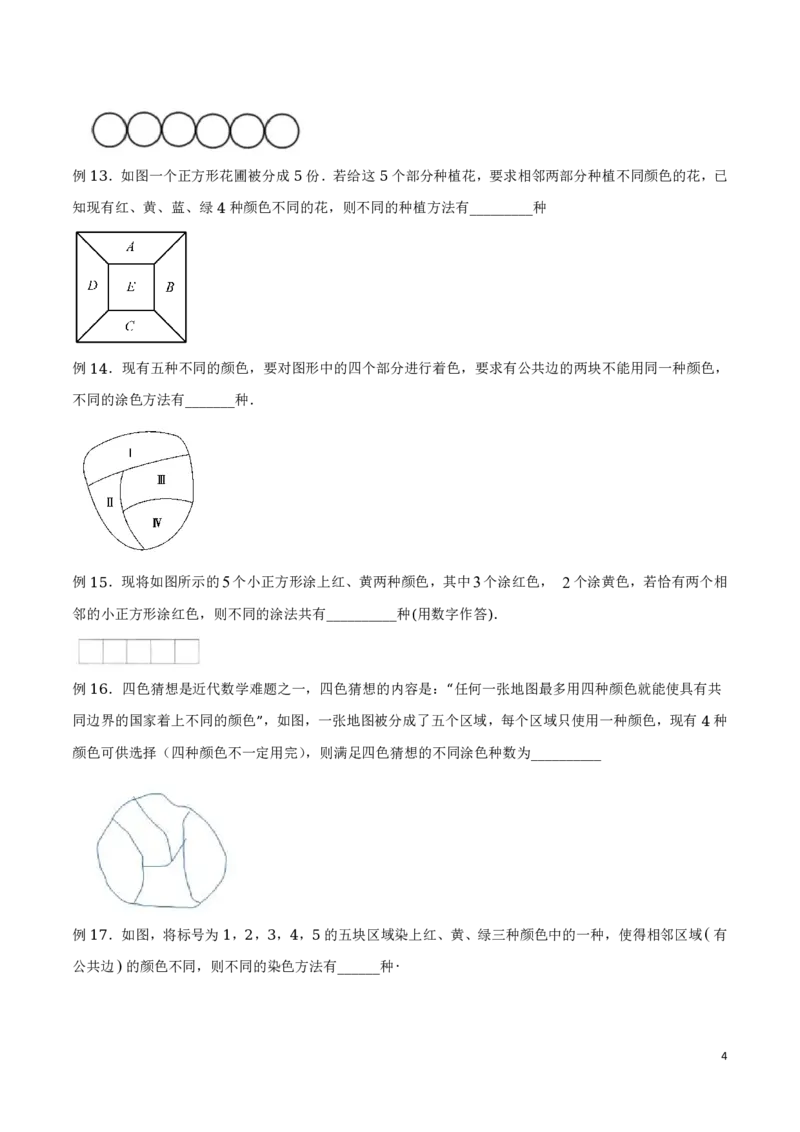
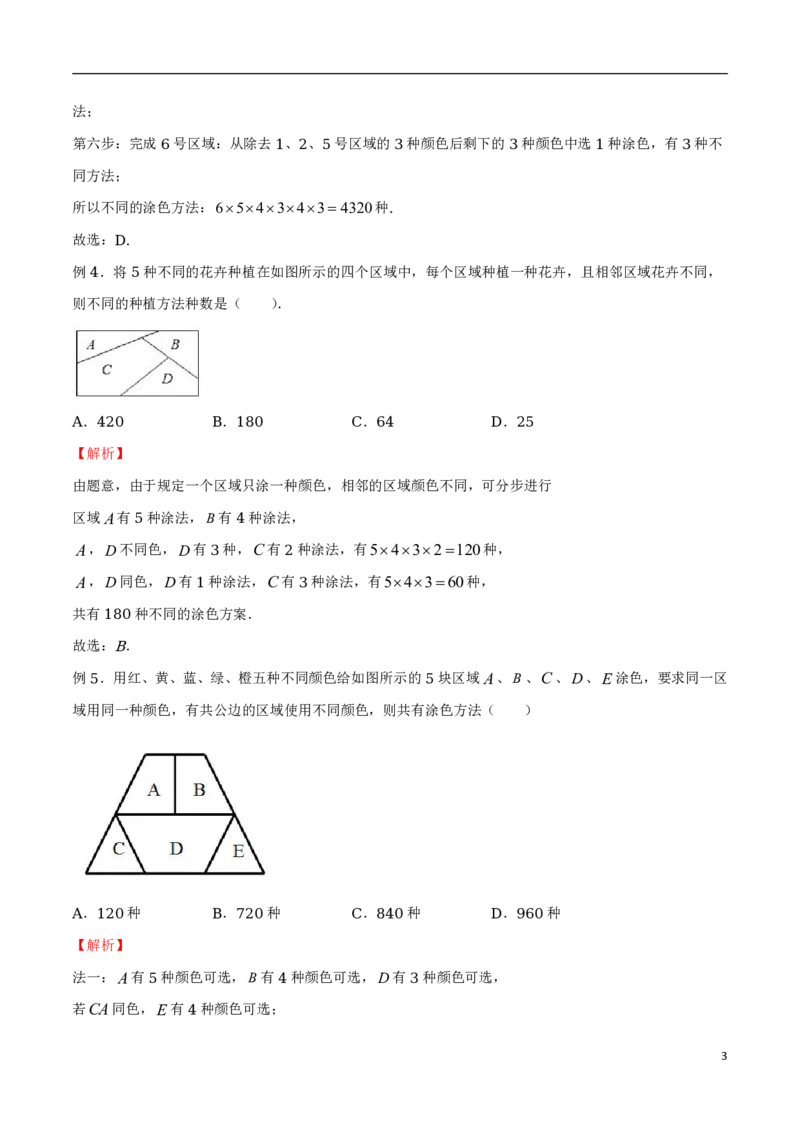
专题 染色问题 6 例 ．如图所示的几何体由三棱锥PABC与三棱柱ABCABC 组合而成，现用3种不同颜色对这个几 1 1 1 1 何体的表面涂色 底面ABC 不涂色 ，要求相邻的面均不同色，则不同的涂色方案共有（ ） 1 1 1 ( ) ．6种 ．9种 A B ．12种 ．36种 C D 例 ．如图，用四种不同的颜色给图中的 ， ， ， ， ， ， 七个点涂色，要求每个点涂一种颜色， 2 A B C D E F G 且图中每条线段的两个端点涂不同颜色，则不同的涂色方法有（ ） ． 种 ． 种 ． 种 ． 种 A 192 B 336 C 600 D 624 例 ．现有 种不同的颜色，给图中的 个区域涂色，要求相邻区域不同色，则不同的涂色方法共有（ ） 3 6 6 ． 种 ． 种 ． 种 ． 种 A 720 B 1440 C 2880 D 4320 例 ．将 种不同的花卉种植在如图所示的四个区域中，每个区域种植一种花卉，且相邻区域花卉不同， 4 5 则不同的种植方法种数是（ ）． 1． ． ． ． A 420 B 180 C 64 D 25 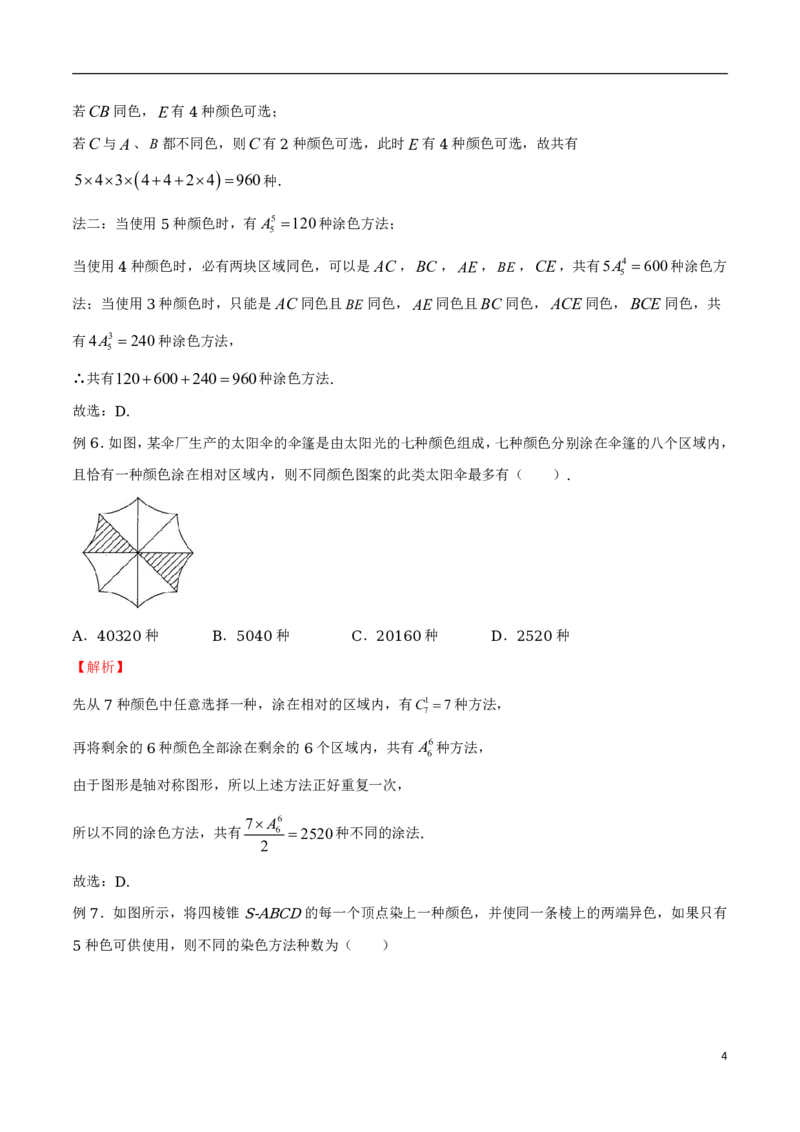例 ．用红、黄、蓝、绿、橙五种不同颜色给如图所示的 块区域A、B、C、D、E涂色，要求同一区 5 5 域用同一种颜色，有共公边的区域使用不同颜色，则共有涂色方法（ ） ． 种 ． 种 ． 种 ． 种 A 120 B 720 C 840 D 960 例 ．如图，某伞厂生产的太阳伞的伞篷是由太阳光的七种颜色组成，七种颜色分别涂在伞篷的八个区域内， 6 且恰有一种颜色涂在相对区域内，则不同颜色图案的此类太阳伞最多有（ ） . 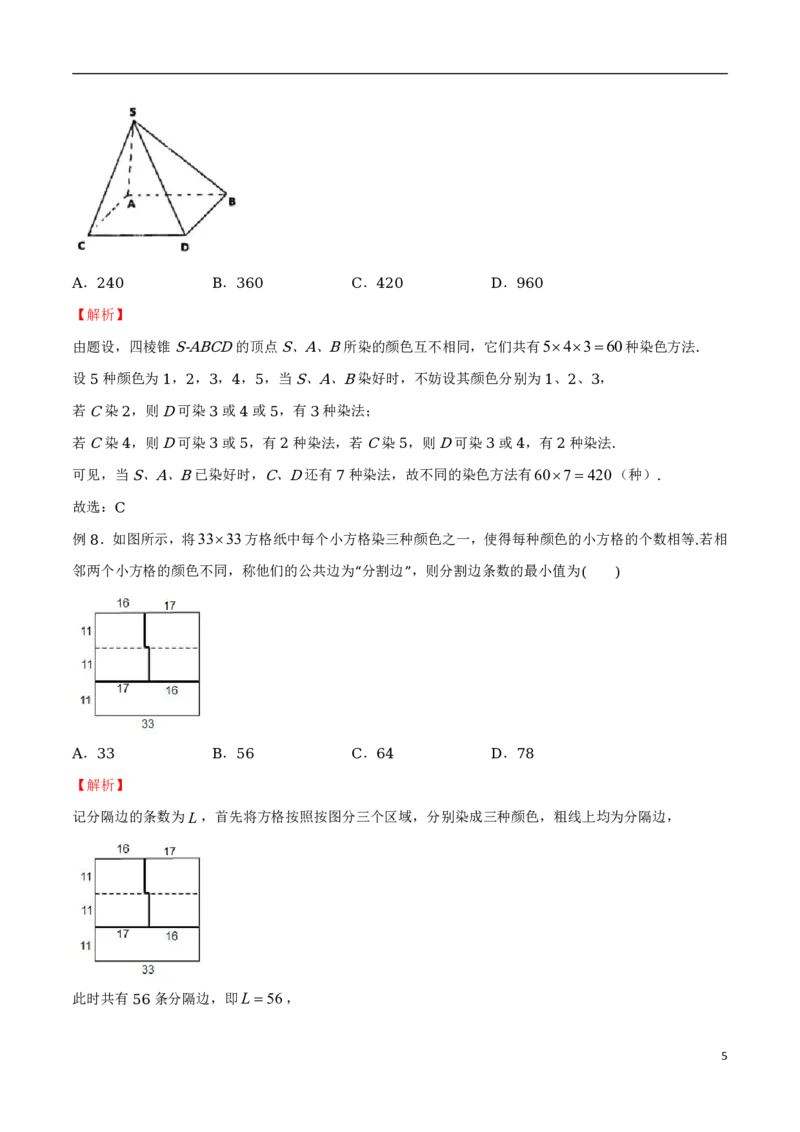． 种 ． 种 ． 种 ． 种 A 40320 B 5040 C 20160 D 2520 例 ．如图所示，将四棱锥 的每一个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有 7 S-ABCD 种色可供使用，则不同的染色方法种数为（ ） 5 ． ． ． ． A 240 B 360 C 420 D 960 例 ．如图所示，将3333方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等 若相 8 . 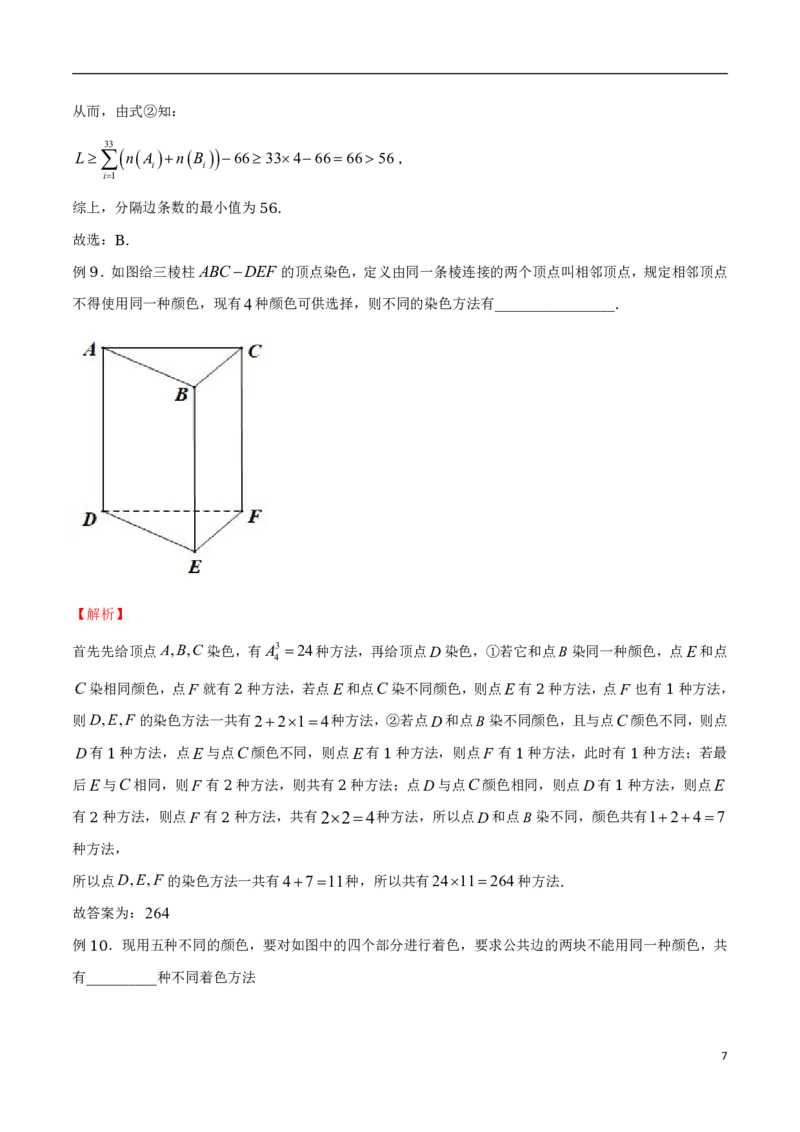邻两个小方格的颜色不同，称他们的公共边为 分割边 ，则分割边条数的最小值为 “ ” ( ) 2． ． ． ． A 33 B 56 C 64 D 78 例 ．如图给三棱柱ABCDEF 的顶点染色，定义由同一条棱连接的两个顶点叫相邻顶点，规定相邻顶 9 点不得使用同一种颜色，现有4种颜色可供选择，则不同的染色方法有 _________________. 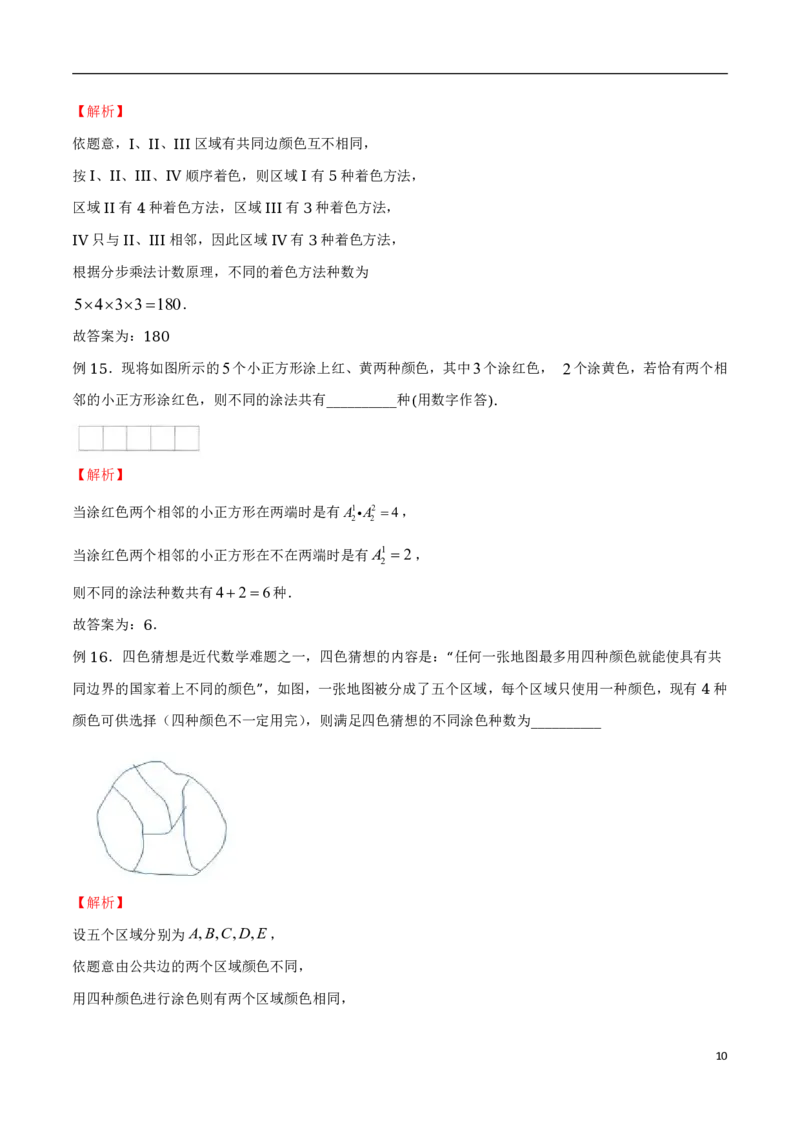例 ．现用五种不同的颜色，要对如图中的四个部分进行着色，要求公共边的两块不能用同一种颜色，共 10 有 种不同着色方法 __________ 例 ．如图所示的五个区域中，中心区E域是一幅图画，现要求在其 ． 余 ． 四 ． 个 ． 区 ． 域 ． 中 ． 涂 ． 色 ． ，有四种颜色可供 11 选择．要求每个区域只涂一种颜色且相邻区域所涂颜色不同，则不同的涂色方法种数为 ． ______ 例 ．从红、黄、蓝、黑四种颜色中选出 种颜色，给如图所示的六个相连的圆涂色，若每种颜色只能涂 12 3 两个圆，且相邻两个圆所涂颜色不能相同，则不同的涂色方案的种数是 ________. 3例 ．如图一个正方形花圃被分成 份．若给这 个部分种植花，要求相邻两部分种植不同颜色的花，已 13 5 5 知现有红、黄、蓝、绿 种颜色不同的花，则不同的种植方法有 种 4 _________ 例 ．现有五种不同的颜色，要对图形中的四个部分进行着色，要求有公共边的两块不能用同一种颜色， 14 不同的涂色方法有 种． _______ 例 ．现将如图所示的5个小正方形涂上红、黄两种颜色，其中3个涂红色， 2个涂黄色，若恰有两个相 15 邻的小正方形涂红色，则不同的涂法共有 种 用数字作答 __________ ( ). 例 ．四色猜想是近代数学难题之一，四色猜想的内容是： 任何一张地图最多用四种颜色就能使具有共 16 “ 同边界的国家着上不同的颜色 ，如图，一张地图被分成了五个区域，每个区域只使用一种颜色，现有 种 ” 4 颜色可供选择（四种颜色不一定用完），则满足四色猜想的不同涂色种数为 __________ 例 ．如图，将标号为 ， ， ， ， 的五块区域染上红、黄、绿三种颜色中的一种，使得相邻区域(有 公共 17 边)的颜色不同，则 1 不同 2 的染 3 色 4 方法 5 有 种. 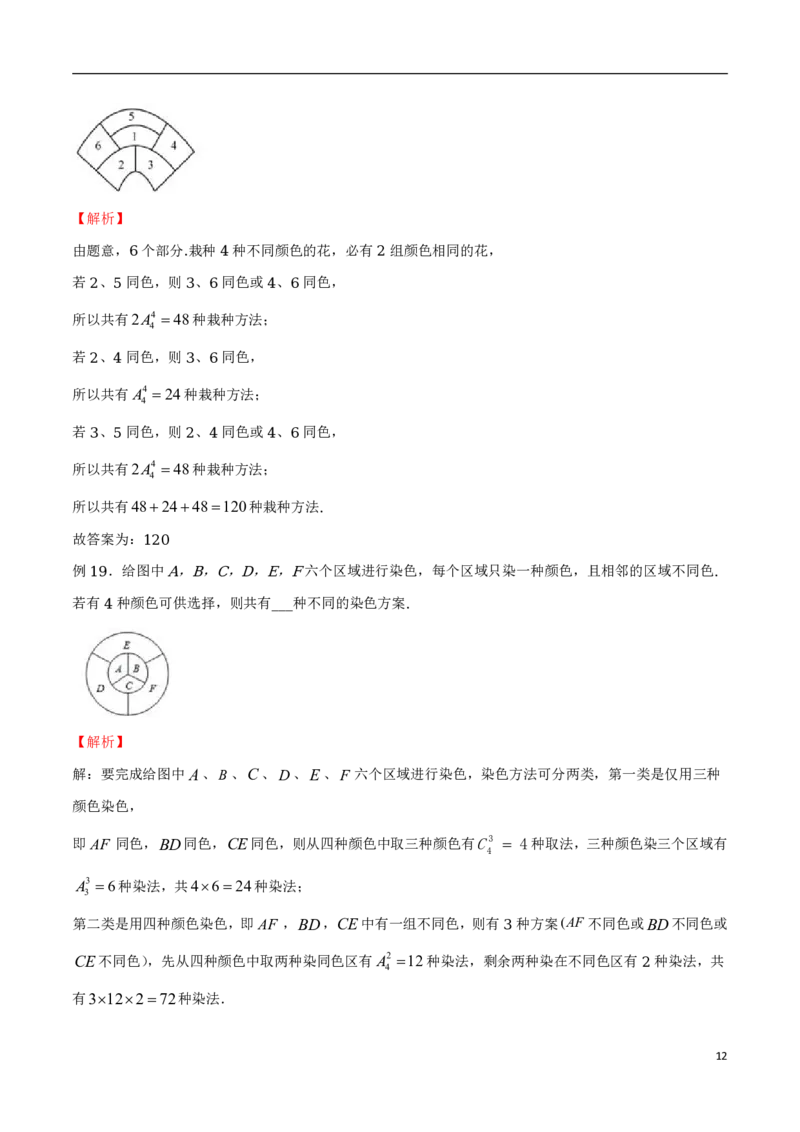______ 4例 ．某城市在中心广场建造一个花圃，花圃分为 个部分 现要栽种 种不同颜色的花，每部分栽种一 18 6 . 4 种且相邻部分不能栽种同样颜色的花，则不同的栽种方法有 种 （用数字作答） ______ . 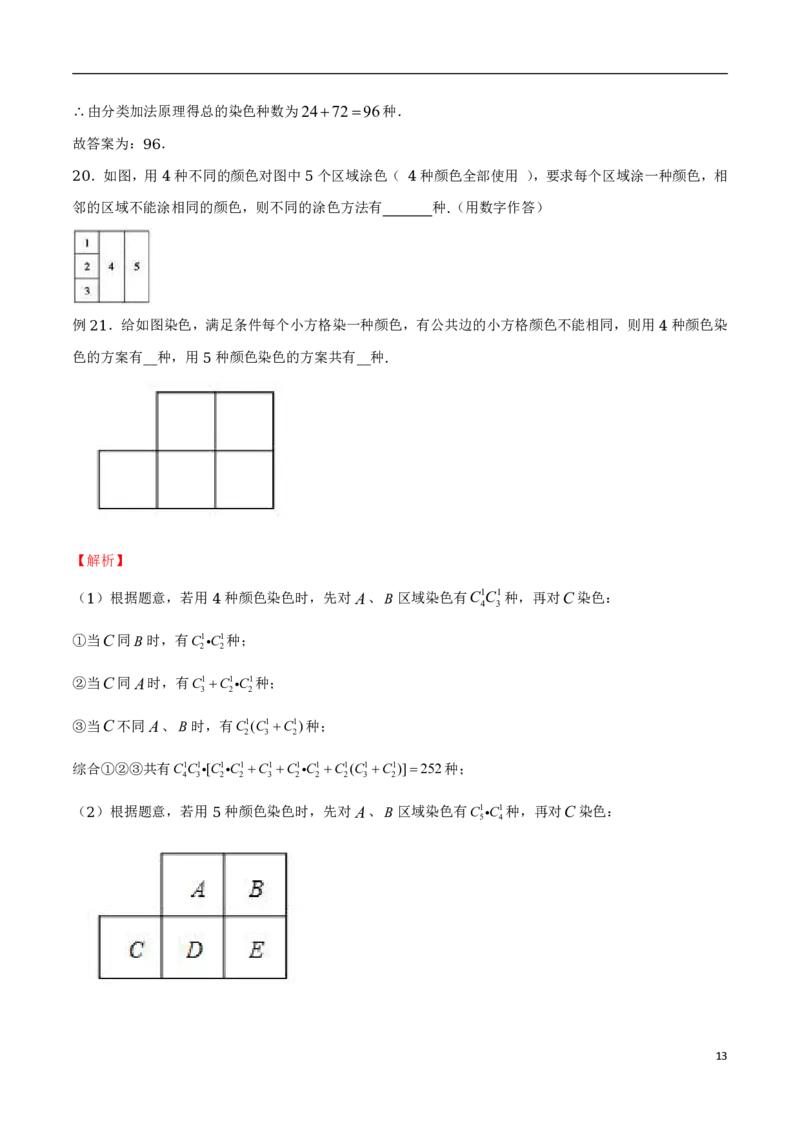例 ．给图中 ， ， ， ， ， 六个区域进行染色，每个区域只染一种颜色，且相邻的区域不同色 19 A B C D E F . 若有 种颜色可供选择，则共有 种不同的染色方案 4 ___ . 例 ．如图，用 种不同的颜色对图中 个区域涂色（ 种颜色全部使用 ），要求每个区域涂一种颜色， 20 4 5 4 相邻的区域不能涂相同的颜色，则不同的涂色方法有 种 （用数字作答） . 例 ．给如图染色，满足条件每个小方格染一种颜色，有公共边的小方格颜色不能相同，则用 种颜色染 21 4 色的方案有 种，用 种颜色染色的方案共有 种 __ 5 __ . 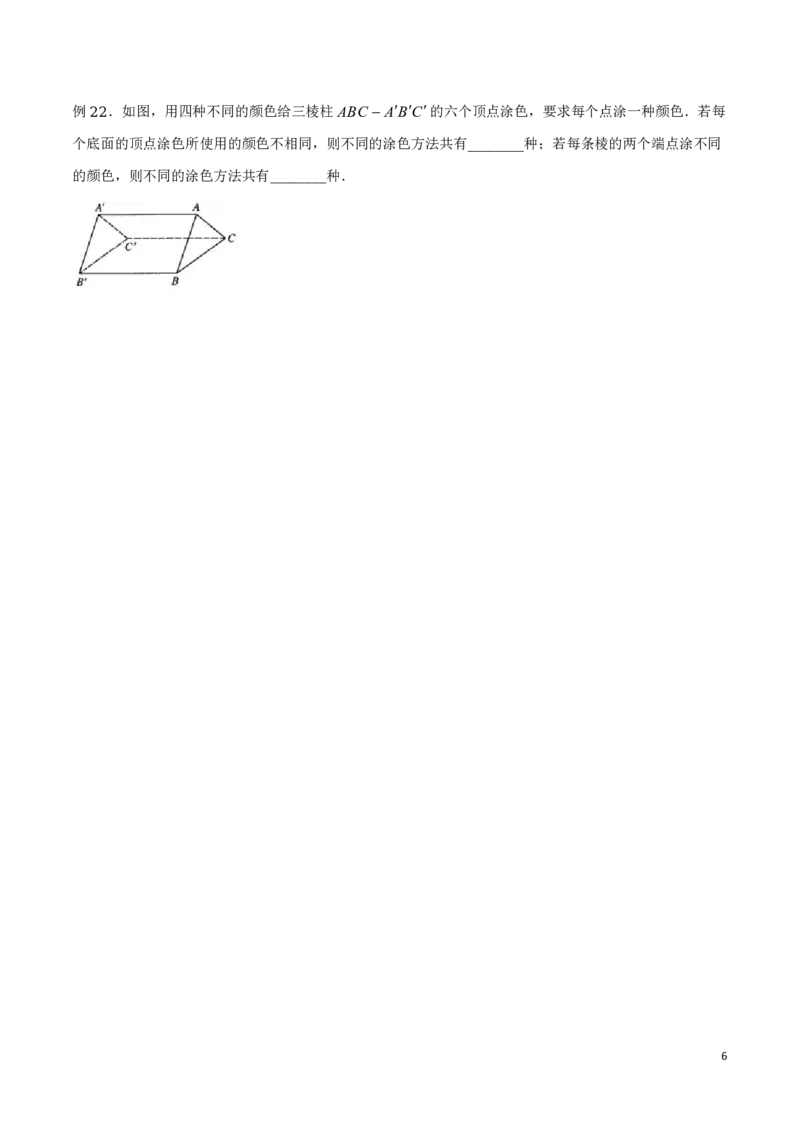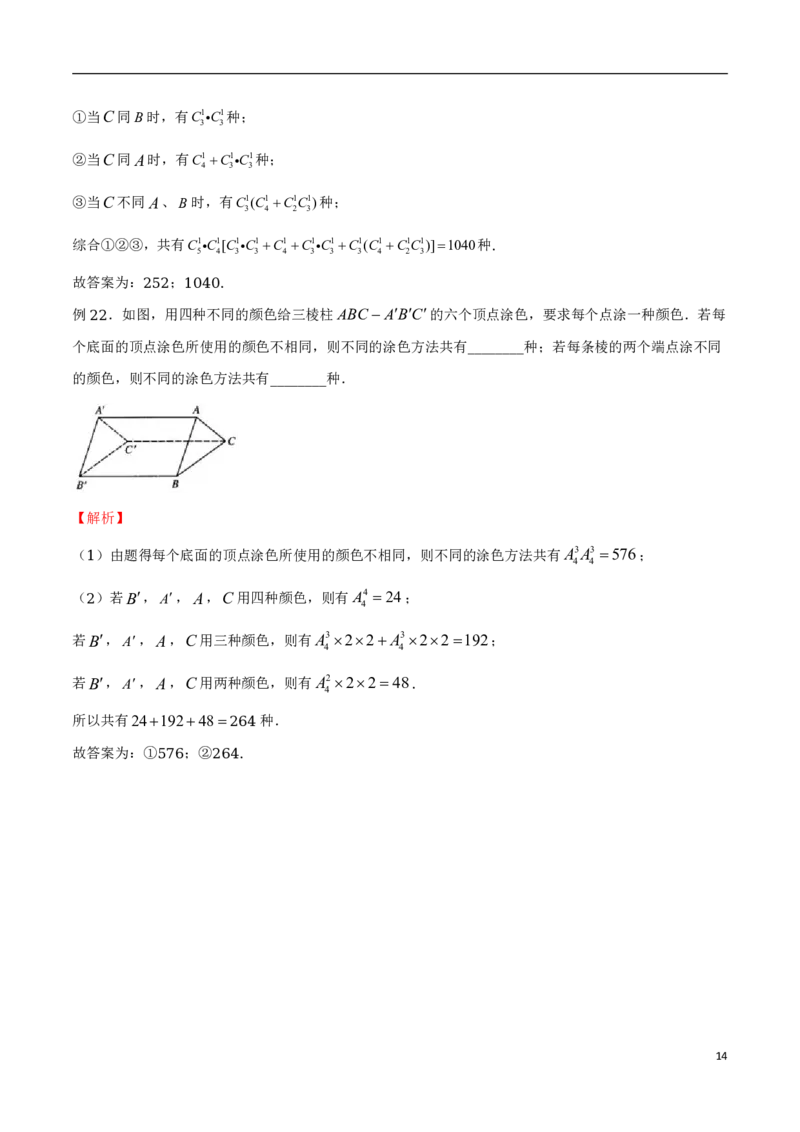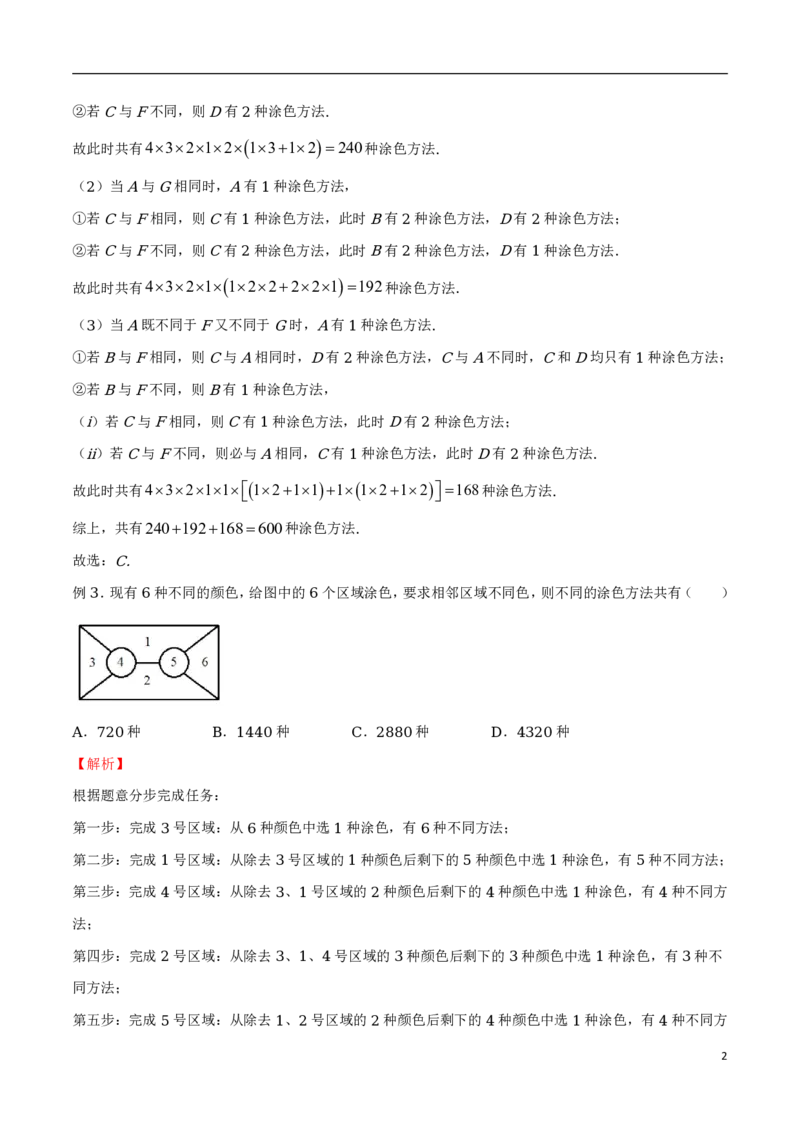5例 ．如图，用四种不同的颜色给三棱柱ABC  ABC的六个顶点涂色，要求每个点涂一种颜色．若每 22 个底面的顶点涂色所使用的颜色不相同，则不同的涂色方法共有 种；若每条棱的两个端点涂不同 ________ 的颜色，则不同的涂色方法共有 种． ________ 6专题 染色问题 6 例 ．如图所示的几何体由三棱锥PABC与三棱柱ABCABC 组合而成，现用3种不同颜色对这个几 1 1 1 1 何体的表面涂色 底面ABC 不涂色 ，要求相邻的面均不同色，则不同的涂色方案共有（ ） 1 1 1 ( ) ．6种 ．9种 A B ．12种 ．36种 C D 【解析】 先涂三棱锥PABC的三个侧面，有C1C1C1 6种情况，然后涂三棱柱的三个侧面，有C1C1C1 2种情 3 2 1 2 1 1 况，共有6212种不同的涂法． 故选： ． C 例 ．如图，用四种不同的颜色给图中的 ， ， ， ， ， ， 七个点涂色，要求每个点涂一种颜色， 2 A B C D E F G 且图中每条线段的两个端点涂不同颜色，则不同的涂色方法有（ ） ． 种 ． 种 ． 种 ． 种 A 192 B 336 C 600 D 624 【解析】 由题意，点 ， ， 分别有 ， ， 种涂法， E F G 4 3 2 （ ）当 与 相同时， 有 种涂色方法，此时 有 种涂色方法， 1 A F A 1 B 2 ①若 与 相同，则 有 种涂色方法，此时 有 种涂色方法； C F C 1 D 3 1②若 与 不同，则 有 种涂色方法 C F D 2 . 故此时共有43212 1312 240种涂色方法 . （ ）当 与 相同时， 有 种涂色方法， 2 A G A 1 ①若 与 相同，则 有 种涂色方法，此时 有 种涂色方法， 有 种涂色方法； C F C 1 B 2 D 2 ②若 与 不同，则 有 种涂色方法，此时 有 种涂色方法， 有 种涂色方法 C F C 2 B 2 D 1 . 故此时共有4321 122221 192种涂色方法 . （ ）当 既不同于 又不同于 时， 有 种涂色方法 3 A F G A 1 . ①若 与 相同，则 与 相同时， 有 种涂色方法， 与 不同时， 和 均只有 种涂色方法； B F C A D 2 C A C D 1 ②若 与 不同，则 有 种涂色方法， B F B 1 （ ）若 与 相同，则 有 种涂色方法，此时 有 种涂色方法； i C F C 1 D 2 （ ）若 与 不同，则必与 相同， 有 种涂色方法，此时 有 种涂色方法 ii C F A C 1 D 2 . 故此时共有43211   1211 1 1212   168种涂色方法 . 综上，共有240192168600种涂色方法 . 故选： C. 例 ．现有 种不同的颜色，给图中的 个区域涂色，要求相邻区域不同色，则不同的涂色方法共有（ ） 3 6 6 ． 种 ． 种 ． 种 ． 种 A 720 B 1440 C 2880 D 4320 【解析】 根据题意分步完成任务： 第一步：完成 号区域：从 种颜色中选 种涂色，有 种不同方法； 3 6 1 6 第二步：完成 号区域：从除去 号区域的 种颜色后剩下的 种颜色中选 种涂色，有 种不同方法； 1 3 1 5 1 5 第三步：完成 号区域：从除去 、 号区域的 种颜色后剩下的 种颜色中选 种涂色，有 种不同方 4 3 1 2 4 1 4 法； 第四步：完成 号区域：从除去 、 、 号区域的 种颜色后剩下的 种颜色中选 种涂色，有 种不 2 3 1 4 3 3 1 3 同方法； 第五步：完成 号区域：从除去 、 号区域的 种颜色后剩下的 种颜色中选 种涂色，有 种不同方 5 1 2 2 4 1 4 2法； 第六步：完成 号区域：从除去 、 、 号区域的 种颜色后剩下的 种颜色中选 种涂色，有 种不 6 1 2 5 3 3 1 3 同方法； 所以不同的涂色方法：6543434320种 . 故选： D. 例 ．将 种不同的花卉种植在如图所示的四个区域中，每个区域种植一种花卉，且相邻区域花卉不同， 4 5 则不同的种植方法种数是（ ）． ． ． ． ． A 420 B 180 C 64 D 25 【解析】 由题意，由于规定一个区域只涂一种颜色，相邻的区域颜色不同，可分步进行 区域A有 种涂法，B有 种涂法， 5 4 A，D不同色，D有 种，C有 种涂法，有5432120种， 3 2 A，D同色，D有 种涂法，C有 种涂法，有54360种， 1 3 共有 种不同的涂色方案． 180 故选： ． B 例 ．用红、黄、蓝、绿、橙五种不同颜色给如图所示的 块区域A、B、C、D、E涂色，要求同一区 5 5 域用同一种颜色，有共公边的区域使用不同颜色，则共有涂色方法（ ） ． 种 ． 种 ． 种 ． 种 A 120 B 720 C 840 D 960 【解析】 法一：A有 种颜色可选，B有 种颜色可选，D有 种颜色可选， 5 4 3 若CA同色，E有 种颜色可选； 4 3若CB同色，E有 种颜色可选； 4 若C与A、B都不同色，则C有 种颜色可选，此时E有 种颜色可选，故共有 2 4 543 4424 960种． 法二：当使用 种颜色时，有A5 120种涂色方法； 5 5 当使用 种颜色时，必有两块区域同色，可以是AC，BC，AE，BE ，CE，共有5A4 600种涂色方 5 4 法；当使用 种颜色时，只能是AC同色且BE 同色，AE同色且BC同色，ACE同色，BCE同色，共 3 有4A3 240种涂色方法， 5 ∴共有120600240960种涂色方法 . 故选： D. 例 ．如图，某伞厂生产的太阳伞的伞篷是由太阳光的七种颜色组成，七种颜色分别涂在伞篷的八个区域内， 6 且恰有一种颜色涂在相对区域内，则不同颜色图案的此类太阳伞最多有（ ） . ． 种 ． 种 ． 种 ． 种 A 40320 B 5040 C 20160 D 2520 【解析】 先从 种颜色中任意选择一种，涂在相对的区域内，有C1 7种方法， 7 7 再将剩余的 种颜色全部涂在剩余的 个区域内，共有A6种方法， 6 6 6 由于图形是轴对称图形，所以上述方法正好重复一次， 7A6 所以不同的涂色方法，共有 6 2520种不同的涂法 2 . 故选： D. 例 ．如图所示，将四棱锥 的每一个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有 7 S-ABCD 种色可供使用，则不同的染色方法种数为（ ） 5 4． ． ． ． A 240 B 360 C 420 D 960 【解析】 由题设，四棱锥 的顶点 、 、 所染的颜色互不相同，它们共有54360种染色方法 S-ABCD S A B . 设 种颜色为 ， ， ， ， ，当 、 、 染好时，不妨设其颜色分别为 、 、 ， 5 1 2 3 4 5 S A B 1 2 3 若 染 ，则 可染 或 或 ，有 种染法； C 2 D 3 4 5 3 若 染 ，则 可染 或 ，有 种染法，若 染 ，则 可染 或 ，有 种染法 C 4 D 3 5 2 C 5 D 3 4 2 . 可见，当 、 、 已染好时， 、 还有 种染法，故不同的染色方法有607420（种） S A B C D 7 . 故选： C 例 ．如图所示，将3333方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等 若相 8 . 邻两个小方格的颜色不同，称他们的公共边为 分割边 ，则分割边条数的最小值为 “ ” ( ) ． ． ． ． A 33 B 56 C 64 D 78 【解析】 记分隔边的条数为L，首先将方格按照按图分三个区域，分别染成三种颜色，粗线上均为分隔边， 此时共有 条分隔边，即L56， 56 5其次证明：L56， 将将方格的行从上至下依次记为A,A ,,A ，列从左至右依次记为B,B ,B ，行A中方格出现的颜 1 2 33 1 2 33 i 色数记为n  A  ，列B 中方格出现的颜色个数记为n  B  ，三种颜色分别记为c ,c ,c ，对于一种颜色c ， i i i 1 2 3 j     设n c 为含有c 色方格的行数与列数之和，定义当A 行含有c 色方格时， A,c 1，否则 j j i j i j      A,c 0，类似的定义 B,c ， i j i j 所以  33  n  A n  B   33  3    A ,c    B ,c     3 n  c  ， i i i j i j j  i1 i1 i1 j1 1 由于染c 色的格有 332 363个，设含有c 色方格的行有a个，列有b个，则c 色的方格一定再这个a j j j 3 行和b列的交叉方格中， 从而ab363，     所以n c ab 2 ab  2 36338n c 39(j 1,2,3) ①， j j 由于在行A中有n  A  种颜色的方格，于是至少有n  A 1条分隔边， i i i 类似的，在列B 中有n  B  种颜色的方格，于是至少有n  B 1条分隔边， i i i 33 33 33 则L n  A 1   n  B 1   n  A n  B  66 ② i i i i i1 i1 i1 3 n  c  66③ j j1 下面分两种情形讨论， 有一行或一列所有方格同色， (1) 不妨设有一行均为c 色，则方格的 列均含有c 的方格，又c 色的方格有 个 故至少有 行有c 色 1 1 1 1 33 363 , 11 方格，于是n  c 113344④ 1 由①③④得 Ln  c n  c n  c 664439396656， 1 2 3 没有一行也没有一列的所有方格同色 (2) , 则对任意1i33均有n  A 2,n  B 2， i i 6从而，由式②知： 33 L n  A n  B  66 33466 66 56， i i i1 综上，分隔边条数的最小值为 56. 故选： B. 例 ．如图给三棱柱ABCDEF 的顶点染色，定义由同一条棱连接的两个顶点叫相邻顶点，规定相邻顶点 9 不得使用同一种颜色，现有4种颜色可供选择，则不同的染色方法有 _________________. 【解析】 首先先给顶点A,B,C 染色，有A3 24种方法，再给顶点D染色，①若它和点B染同一种颜色，点E和点 4 C染相同颜色，点F 就有 种方法，若点E和点C染不同颜色，则点E有 种方法，点F 也有 种方法， 2 2 1 则D,E,F 的染色方法一共有2214种方法，②若点D和点B染不同颜色，且与点C颜色不同，则点 D有 种方法，点E与点C颜色不同，则点E有 种方法，则点F 有 种方法，此时有 种方法；若最 1 1 1 1 后E与C相同，则F 有 种方法，则共有 种方法；点D与点C颜色相同，则点D有 种方法，则点E 2 2 1 有 种方法，则点F 有 种方法，共有224种方法，所以点D和点B染不同，颜色共有1247 2 2 种方法， 所以点D,E,F 的染色方法一共有4711种，所以共有2411264种方法 . 故答案为：264 例 ．现用五种不同的颜色，要对如图中的四个部分进行着色，要求公共边的两块不能用同一种颜色，共 10 有 种不同着色方法 __________ 7【解析】 先排I，有5 种方法； 然后排II,IV，最后排III： ①当II,IV相同时，方法有44种，故方法数有54480种 . ②当II,IV不同时，方法有433种，故方法数有5433180种 . 综上所述，不同的着色方法数有80180260种 . 故答案为：260 例 ．如图所示的五个区域中，中心区E域是一幅图画，现要求在其 ． 余 ． 四 ． 个 ． 区 ． 域 ． 中 ． 涂 ． 色 ． ，有四种颜色可供 11 选择．要求每个区域只涂一种颜色且相邻区域所涂颜色不同，则不同的涂色方法种数为 ． ______ 【解析】 分三种情况： （ ）用四种颜色涂色，有A4 24种涂法； 4 1 （ ）用三种颜色涂色，有2A3 48种涂法； 4 2 （ ）用两种颜色涂色，有A2 12种涂法； 4 3 所以共有涂色方法24481284 . 故答案为： 84 例 ．从红、黄、蓝、黑四种颜色中选出 种颜色，给如图所示的六个相连的圆涂色，若每种颜色只能涂 12 3 两个圆，且相邻两个圆所涂颜色不能相同，则不同的涂色方案的种数是 ________. 【解析】 8从红、黄、蓝、黑四种颜色中选出 种颜色有 种选法 3 4 . 因为每种颜色只能涂两个圆，且相邻两个圆所涂颜色不能相同，分两类： 一类是，前三个圆用 种颜色，有A3 6种方法，后 个圆也有 种颜色，有C1C1 4种方法，此时不 3 2 2 3 3 3 同方法有 方法； 6×4=24 二类是，前 个圆 种颜色，后 个圆 种颜色，共有C1C1 6方法 3 2 3 2 3 2 . 综上可知，所有的涂法共有4 246 120种方法 . 故答案为： 120 例 ．如图一个正方形花圃被分成 份．若给这 个部分种植花，要求相邻两部分种植不同颜色的花，已 13 5 5 知现有红、黄、蓝、绿 种颜色不同的花，则不同的种植方法有 种 4 _________ 【解析】 先对E部分种植，有 种不同的种植方法； 4 再对A部分种植，又 种不同的种植方法； 3 对C部分种植进行分类： ①若与A相同，D有 种不同的种植方法，B有 种不同的种植方法，共有432248（种）， 2 2 ②若与A不同，C有 种不同的种植方法，D有 种不同的种植方法，B有 种不同的种植方法， 2 1 1 共有4321124（种）， 综上所述，共有 种种植方法． 72 故答案为： 72. 例 ．现有五种不同的颜色，要对图形中的四个部分进行着色，要求有公共边的两块不能用同一种颜色， 14 不同的涂色方法有 种． _______ 9【解析】 依题意， 、 、 区域有共同边颜色互不相同， I II III 按 、 、 、 顺序着色，则区域 有 种着色方法， I II III IV I 5 区域 有 种着色方法，区域 有 种着色方法， II 4 III 3 只与 、 相邻，因此区域 有 种着色方法， IV II III IV 3 根据分步乘法计数原理，不同的着色方法种数为 5433180 . 故答案为： 180 例 ．现将如图所示的5个小正方形涂上红、黄两种颜色，其中3个涂红色， 2个涂黄色，若恰有两个相 15 邻的小正方形涂红色，则不同的涂法共有 种 用数字作答 __________ ( ). 【解析】 当涂红色两个相邻的小正方形在两端时是有A1A2 4， 2 2 当涂红色两个相邻的小正方形在不在两端时是有A1 2， 2 则不同的涂法种数共有426种． 故答案为： ． 6 例 ．四色猜想是近代数学难题之一，四色猜想的内容是： 任何一张地图最多用四种颜色就能使具有共 16 “ 同边界的国家着上不同的颜色 ，如图，一张地图被分成了五个区域，每个区域只使用一种颜色，现有 种 ” 4 颜色可供选择（四种颜色不一定用完），则满足四色猜想的不同涂色种数为 __________ 【解析】 设五个区域分别为A,B,C,D,E， 依题意由公共边的两个区域颜色不同， 用四种颜色进行涂色则有两个区域颜色相同， 10可以是A与C，A与E，B与E同色， 有涂色方法3A4 72； 4 或用三种颜色涂色，则有 组颜色同色， 2 为A与C同色，B与E同色，有涂色方法A3 24， 4 根据分类加法原理，共有涂色方法722496 . 故答案为：96 . 例 ．如图，将标号为 ， ， ， ， 的五块区域染上红、黄、绿三种颜色中的一种，使得相邻区域(有 公共 17 边)的颜色不同，则 1 不同 2 的染 3 色 4 方法 5 有 种. ______ 【解析】 对于 ，有三种颜色可以安排； 1 若 和 颜色相同，有两种安排方法， 有两种安排， 有一种安排，此时共有322112； 2 3 4 5 若 和 颜色不同，则 有两种， 有一种 当 和 相同时， 有两种；当 和 不同，则 有一种， 2 3 2 3 . 5 2 4 5 2 4 此时共有32 21  18，   综上可知，共有121830种染色方法 . 故答案为：30 . 例 ．某城市在中心广场建造一个花圃，花圃分为 个部分 现要栽种 种不同颜色的花，每部分栽种一 18 6 . 4 种且相邻部分不能栽种同样颜色的花，则不同的栽种方法有 种 （用数字作答） ______ . 11【解析】 由题意， 个部分 栽种 种不同颜色的花，必有 组颜色相同的花， 6 . 4 2 若 、 同色，则 、 同色或 、 同色， 2 5 3 6 4 6 所以共有2A4 48种栽种方法； 4 若 、 同色，则 、 同色， 2 4 3 6 所以共有A4 24种栽种方法； 4 若 、 同色，则 、 同色或 、 同色， 3 5 2 4 4 6 所以共有2A4 48种栽种方法； 4 所以共有482448120种栽种方法 . 故答案为： 120 例 ．给图中 ， ， ， ， ， 六个区域进行染色，每个区域只染一种颜色，且相邻的区域不同色 19 A B C D E F . 若有 种颜色可供选择，则共有 种不同的染色方案 4 ___ . 【解析】 解：要完成给图中A、B、C、D、E、F 六个区域进行染色，染色方法可分两类，第一类是仅用三种 颜色染色， 即AF 同色，BD同色，CE同色，则从四种颜色中取三种颜色有C3  4种取法，三种颜色染三个区域有 4 A3 6种染法，共4624种染法； 3 第二类是用四种颜色染色，即AF ，BD，CE中有一组不同色，则有 种方案(AF 不同色或BD不同色或 3 CE不同色），先从四种颜色中取两种染同色区有A2 12种染法，剩余两种染在不同色区有 种染法，共 4 2 有312272种染法． 12由分类加法原理得总的染色种数为247296种． 故答案为： ． 96 ．如图，用 种不同的颜色对图中 个区域涂色（ 种颜色全部使用 ），要求每个区域涂一种颜色，相 20 4 5 4 邻的区域不能涂相同的颜色，则不同的涂色方法有 种 （用数字作答） . 例 ．给如图染色，满足条件每个小方格染一种颜色，有公共边的小方格颜色不能相同，则用 种颜色染 21 4 色的方案有 种，用 种颜色染色的方案共有 种 __ 5 __ . 【解析】 （ ）根据题意，若用 种颜色染色时，先对A、B区域染色有C1C1种，再对C染色： 4 3 1 4 ①当C同B时，有C1C1种； 2 2 ②当C同A时，有C1C1C1种； 3 2 2 ③当C不同A、B时，有C1(C1C1)种； 2 3 2 综合①②③共有C1C1[C1C1C1C1C1C1(C1C1)]252种； 4 3 2 2 3 2 2 2 3 2 （ ）根据题意，若用 种颜色染色时，先对A、B区域染色有C1C1种，再对C染色： 5 4 2 5 13①当C同B时，有C1C1种； 3 3 ②当C同A时，有C1C1C1种； 4 3 3 ③当C不同A、B时，有C1(C1C1C1)种； 3 4 2 3 综合①②③，共有C1C1[C1C1C1C1C1C1(C1C1C1)]1040种 5 4 3 3 4 3 3 3 4 2 3 . 故答案为： ； 252 1040. 例 ．如图，用四种不同的颜色给三棱柱ABC ABC的六个顶点涂色，要求每个点涂一种颜色．若每 22 个底面的顶点涂色所使用的颜色不相同，则不同的涂色方法共有 种；若每条棱的两个端点涂不同 ________ 的颜色，则不同的涂色方法共有 种． ________ 【解析】 （ ）由题得每个底面的顶点涂色所使用的颜色不相同，则不同的涂色方法共有A3A3 576； 4 4 1 （ ）若B，A，A，C用四种颜色，则有A4 24； 4 2 若B，A，A，C用三种颜色，则有A322 A322192； 4 4 若B，A，A，C用两种颜色，则有A22248 4 . 所以共有2419248 种． 264 故答案为：① ；② 576 264. 14