四川省内江市第六中学2023-2024学年高三上学期第一次月考理数(1)_2023年11月_0211月合集_2024届四川省内江市第六中学高三上学期第一次月考

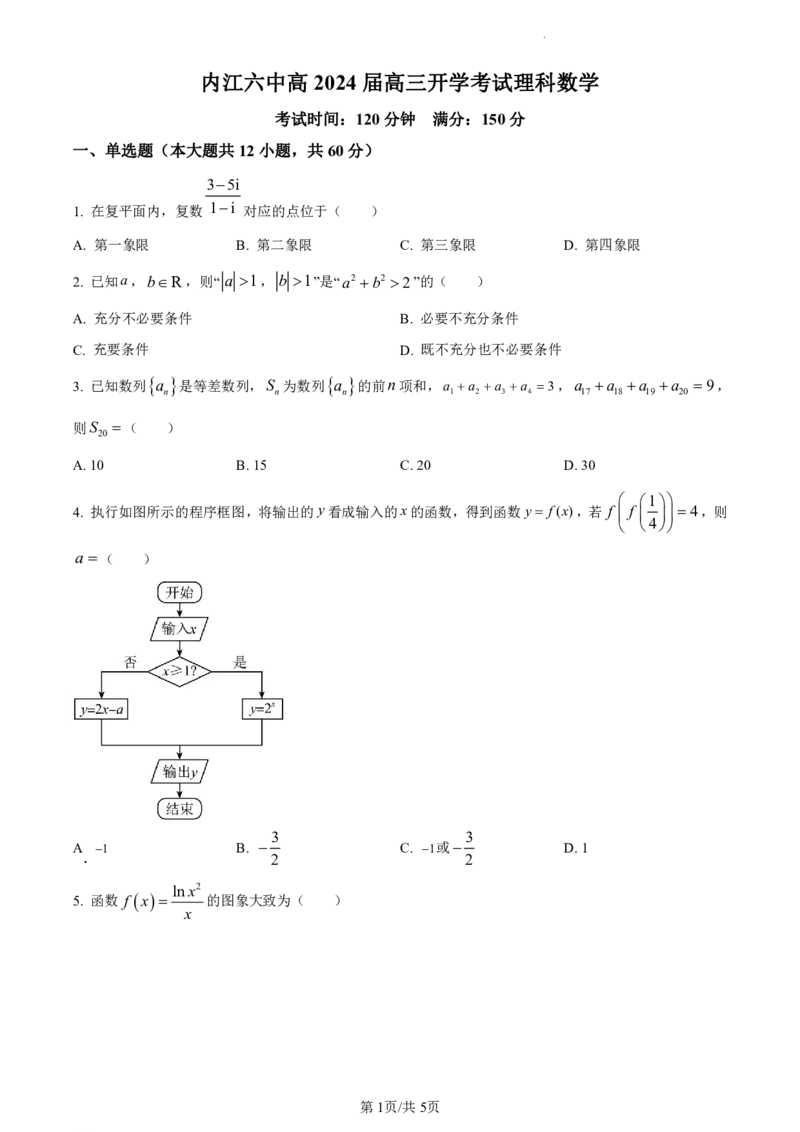
内江六中高 2024 届高三开学考试理科数学 考试时间：120分钟 满分：150分 一、单选题（本大题共 12小题，共 60分） 35i 1. 在复平面内，复数 1i 对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2. 已知a，bR，则“ a 1， b 1”是“a2 b2 2”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 3. 已知数列  a  是等差数列，S 为数列  a  的前n项和，a a a a 3，a a a a  9， n n n 1 2 3 4 17 18 19 20 则S （ ） 20 A.10 B.15 C.20 D.30  1 4. 执行如图所示的程序框图，将输出的y看成输入的x的函数，得到函数y f(x)，若 f  f   4，则  4 a （ ） 3 3 A 1 B.  C. 1或 D.1 . 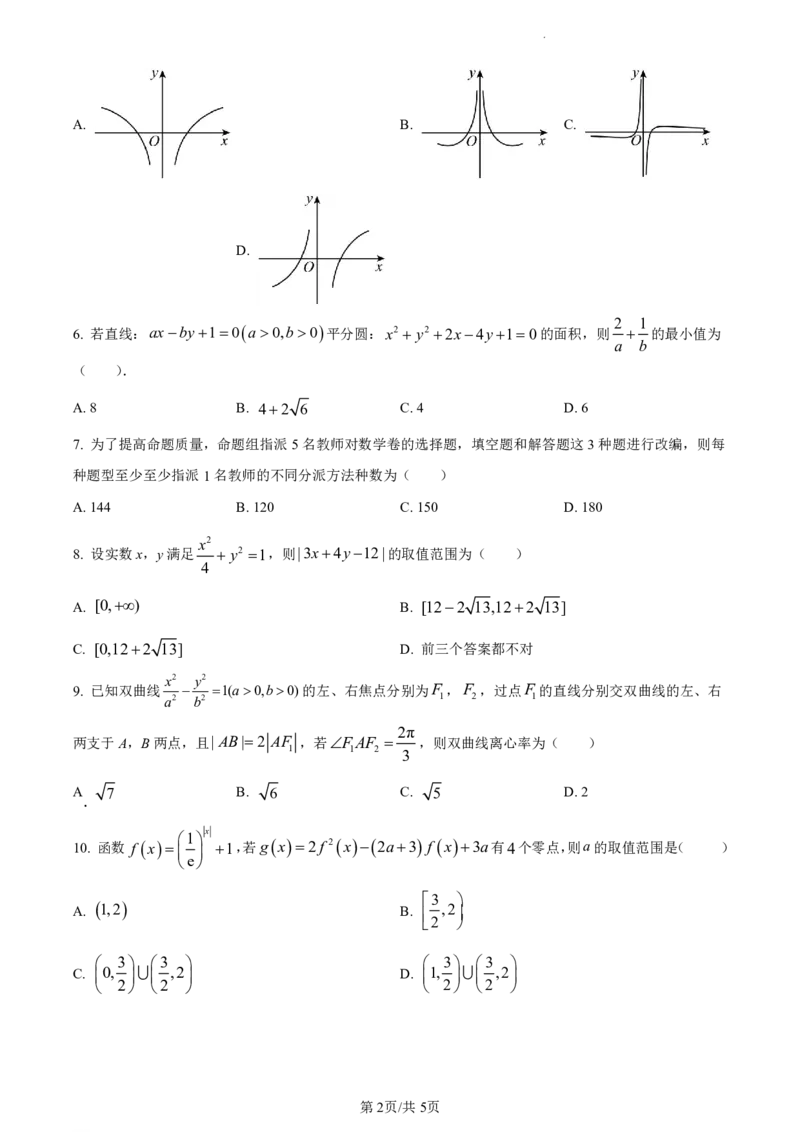2 2 lnx2 5. 函数 f  x  的图象大致为（ ） x 第1页/共5页 学科网（北京）股份有限公司A. B. C. D. 2 1 6. 若直线：axby10a 0,b0平分圆：x2  y2 2x4y10的面积，则  的最小值为 a b （ ）． A.8 B. 42 6 C.4 D.6 7. 为了提高命题质量，命题组指派5名教师对数学卷的选择题，填空题和解答题这3种题进行改编，则每 种题型至少至少指派1名教师的不同分派方法种数为（ ） A.144 B.120 C.150 D.180 x2 8. 设实数x，y满足  y2 1，则|3x4y12|的取值范围为（ ） 4 A. [0,) B. [122 13,122 13] C. [0,122 13] D. 前三个答案都不对 x2 y2 9. 已知双曲线  1(a0,b0)的左、右焦点分别为F ，F ，过点F 的直线分别交双曲线的左、右 a2 b2 1 2 1 2π 两支于A，B两点，且| AB|2 AF ，若FAF  ，则双曲线离心率为（ ） 1 1 2 3 A 7 B. 6 C. 5 D.2 . x 1 10. 函数 f  x    1，若g  x 2f 2 x  2a3  f  x 3a有4个零点，则a的取值范围是（ ） e 3    A. 1,2 B.  ,2 2   3 3   3 3  C. 0,  ,2 D. 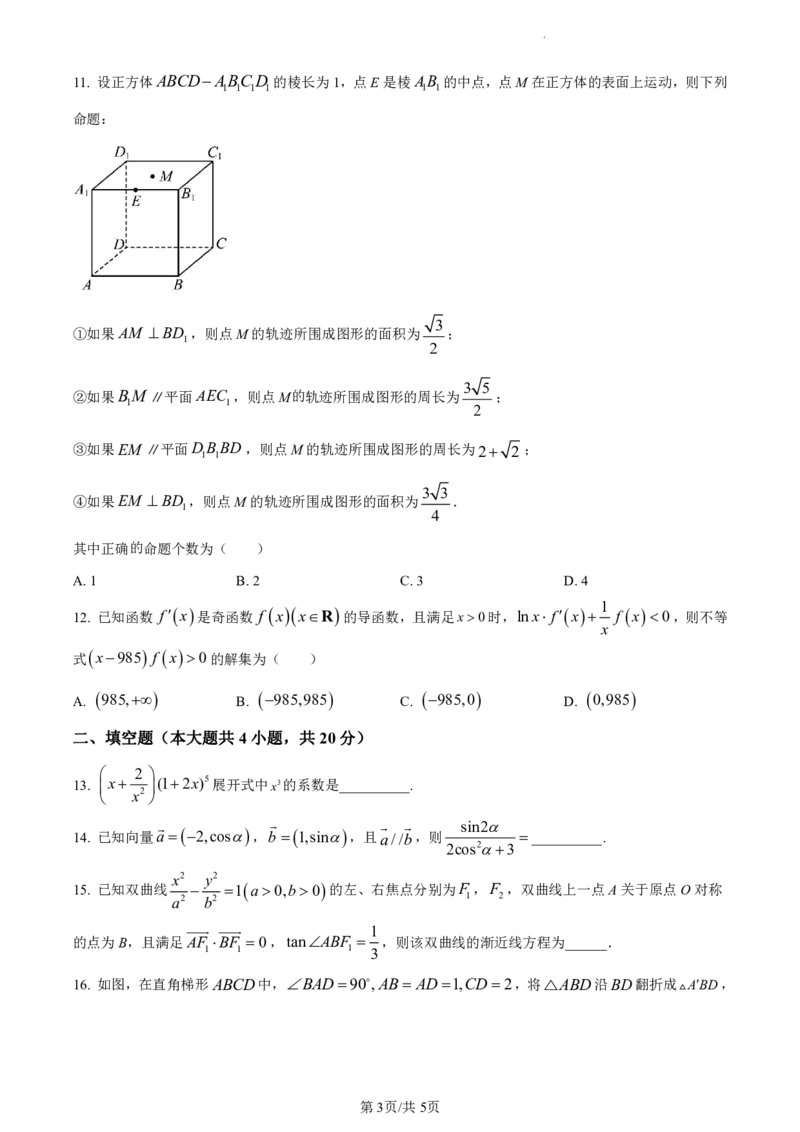1,  ,2  2 2   2 2  第2页/共5页 学科网（北京）股份有限公司11. 设正方体ABCDABCD 的棱长为1，点E是棱AB 的中点，点M在正方体的表面上运动，则下列 1 1 1 1 1 1 命题： 3 ①如果AM BD ，则点M的轨迹所围成图形的面积为 ； 1 2 3 5 ②如果BM ∥平面AEC ，则点M的轨迹所围成图形的周长为 ； 1 1 2 ③如果EM ∥平面DBBD，则点M的轨迹所围成图形的周长为2 2 ； 1 1 3 3 ④如果EM  BD ，则点M的轨迹所围成图形的面积为 ． 1 4 其中正确的命题个数为（ ） A.1 B.2 C.3 D.4 1 12. 已知函数 f  x  是奇函数 f  x  xR  的导函数，且满足x0时，lnx f x  f  x 0，则不等 x 式  x985  f  x 0的解集为（ ） A.  985, B. 985,985  C. 985,0  D.  0,985  二、填空题（本大题共 4小题，共 20分）  2  13. x (12x)5展开式中x3的系数是__________.  x2      sin2 14. 已知向量a 2,cos ，b  1,sin，且a//b，则 __________. 2cos23 x2 y2 15. 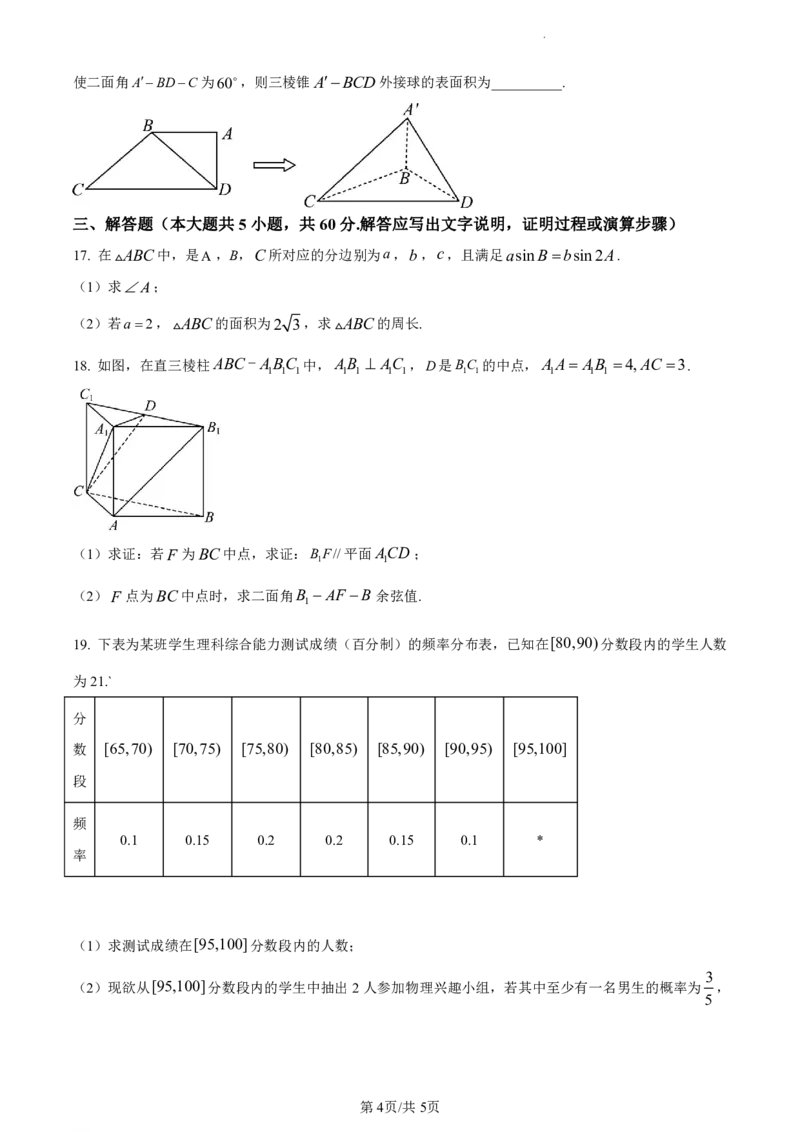已知双曲线  1  a 0,b0 的左、右焦点分别为F ，F ，双曲线上一点A关于原点O对称 a2 b2 1 2   1 的点为B，且满足AF BF  0，tanABF  ，则该双曲线的渐近线方程为______． 1 1 1 3 16. 如图，在直角梯形ABCD中，BAD90,AB AD1,CD2，将△ABD沿BD翻折成ABD， 第3页/共5页 学科网（北京）股份有限公司使二面角ABDC为60，则三棱锥ABCD外接球的表面积为__________. 三、解答题（本大题共 5小题，共 60分.解答应写出文字说明，证明过程或演算步骤） 17. 在ABC中，是A，B，C所对应的分边别为a，b，c，且满足asinBbsin2A. （1）求A； （2）若a2，ABC的面积为2 3，求ABC的周长. 18. 如图，在直三棱柱ABC- ABC 中，AB  AC ，D是BC 的中点，AA AB 4,AC 3. 1 1 1 1 1 1 1 1 1 1 1 1 （1）求证：若F 为BC中点，求证：BF//平面ACD； 1 1 （2）F 点为BC中点时，求二面角B AF B 余弦值. 1 19. 下表为某班学生理科综合能力测试成绩（百分制）的频率分布表，已知在[80,90)分数段内的学生人数 为21.` 分 数 [65,70) [70,75) [75,80) [80,85) [85,90) [90,95) [95,100] 段 频 0.1 0.15 0.2 0.2 0.15 0.1 * 率 （1）求测试成绩在[95,100]分数段内的人数； 3 （2）现欲从[95,100]分数段内的学生中抽出2人参加物理兴趣小组，若其中至少有一名男生的概率为 ， 5 第4页/共5页 学科网（北京）股份有限公司求[95,100]分数段内男生的人数； （3）若在[65,70)分数段内的女生为4人，现欲从[65,70)分数段内的学生中抽出3人参加培优小组，为 分配到此组的3名学生中男生的人数．求的分布列及期望E 20. 已知抛物线M : y2 4x的焦点为F ，过点  2,0  的直线与抛物线M 交于A,B两点，点A在第一象限， O为坐标原点． OP （1）设P为抛物线M 上的动点，求 的取值范围； FP （2）记AOB的面积为S ,△BOF 的面积为S ，求S S 的最小值． 1 2 1 2 1 21. 已知函数 f  x  mxn  ex mx2  2mn  x 在x=1处取得极小值 1. e （1）求实数m,n的值； （2）当x 0, 时，证明： f x  lnx  x  3 . 2 四、选做题（总分 10分，只需要从中选择 1个题目完成）   22. 在直角坐标系xOy中，直线l经过点M 3,1 ，倾斜角为30，以坐标原点O为极点，x轴正半轴为极 轴建立极坐标系，曲线C的极坐标方程为4cos. （1）求直线l的参数方程和曲线C的直角坐标方程； MN （2）设直线l与曲线C相交于A，B两点，弦AB的中点为N，求 的值. MA MB 23. 已知函数 f(x) x2  xa ，aR． （1）当a 1时，求不等式 f (x)5的解集； （2）若对任意xR，都有 f(x)1a成立，求a的取值范围． 第5页/共5页 学科网（北京）股份有限公司