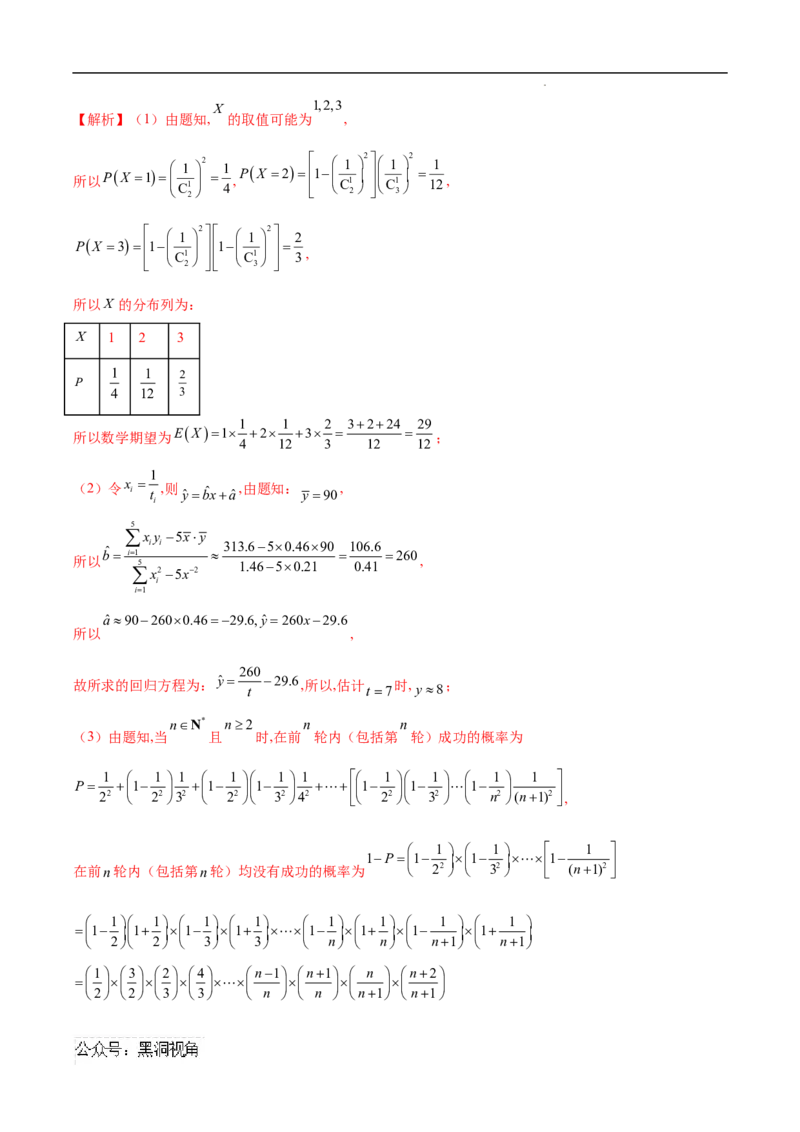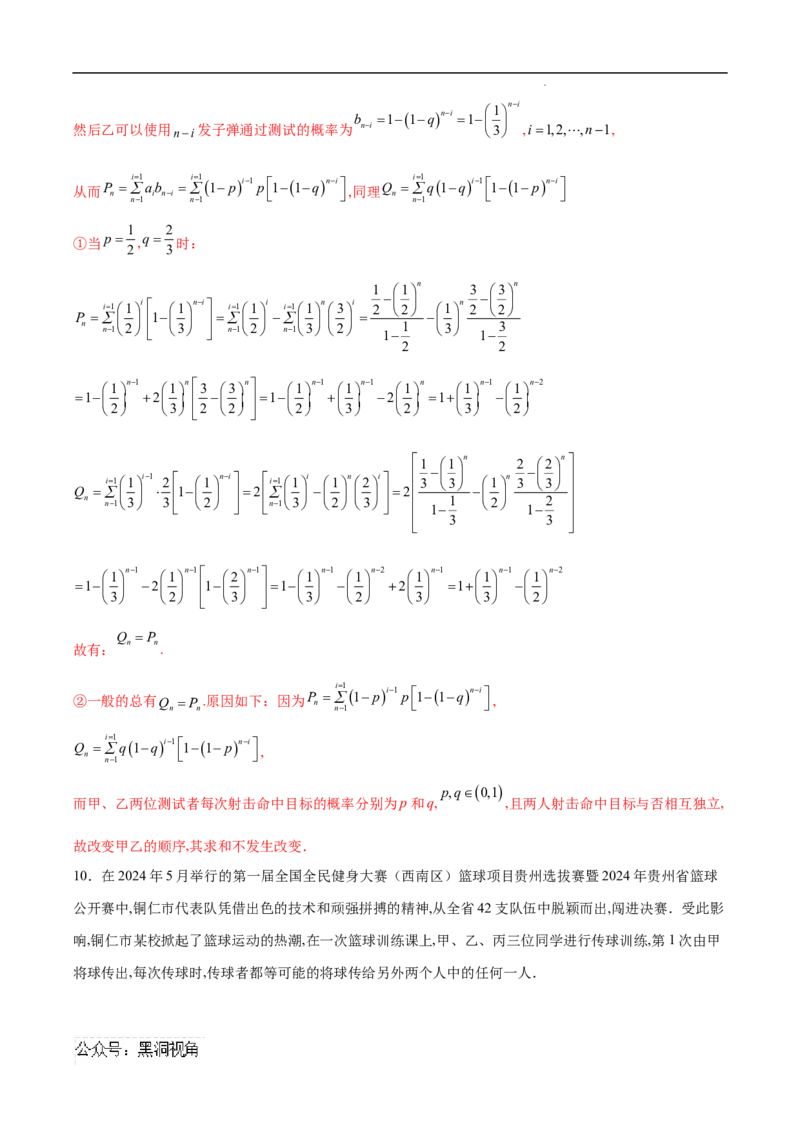专题08数列与概率、立体几何、解析几何的交汇（解析版）_2024-2025高三（6-6月题库）_2025年02月试卷_02272025年高考数学压轴大题必杀技系列·数列

专题 8 数列与概率、立体几何、解析几何的交汇 新高考在试题形式、试卷结构、难度调控等方面深化改革,数列解答题的难度增加,作为压轴题出现 的概率变大,而数列与其他知识的交汇备受青睐,如2024年新高考全国卷I第19题考查的是数列与概率的 交汇,2024年新高考全国卷II第19题考查的是数列与解析几何的交汇,本专题总结数列与概率、立体几何、 解析几何交汇的常见类型及求解,供大家参考. （一）数列与排列组合的交汇 对于排列数 与组合数 而言,当 变动时对应的一列数就可以看作数列,所以与排列数与组合数有关的 等式与不等式问题,大多可以看作数列求解. 【例1】（1）我们学过组合恒等式 ,实际上可以理解为 ,请你利用这个观 点快速求解： .（计算结果用组合数表示） （2）（i）求证： ； （ii）求值： . 【解析】（1） 学科网（北京）股份有限公司； （2）（i） ； （ii） 由（i）得 , 则有 , 原式 构造数列 ,令 ,则 , 所以 所以 ,即 , 即 ,所以 ,即数列 是周期为6的数列. 又因为 , 所以 . 【例2】绿化美化环境,建设美丽乡村.某村拟将村外的空地分成五块（如图1）,种植花草（中间的圆圈不种 植）,现有四种不同的花卉供选择,要求每一块种植一种花,相邻区域种不同的花卉,设所种花卉的种数为X . 学科网（北京）股份有限公司(1)求X 的分布列与期望； n1n2 n1 (2)若将空地分成 个区域（图2）,在这 个区域上种植花卉,要求相邻区域种不同的花卉,现有5 种不同的花卉供选择,问有多少种不同的种植方法？ X A2 12 【解析】（1） 的所有可能值为2,3,4.若种两种花卉,则种植方法有 4 ； C3C1A3 48 A4 24 若种三种花卖,则种植方法有 4 2 3 ；若种四种花卉,则种植方法有 4 ； 所有的种植方法有12482484. 12 1 48 4 24 2 PX 2  PX 2  PX 2  所以 , , , 84 7 84 7 84 7 所以X 的分布列为 X 2 3 4 1 4 2 P 7 7 7 1 4 2 22 的期望EX2 3 4  . X 7 7 7 7 A C1 5 （2）分两步,第一步种植区域 0,有 5 种种植方法； A ~ A n a 1 n n 第二步种植区域 ,在 块区域种植不同的花卉（有4种花卉供选择）,设不同的种植方法有 种. a 4312 a 43224 显然 2 , 3 ； n4 A A A A 当 时, 1有4种种植方法, 2有3种种植方法,… n有3种种植方法（不论是否与 1同种）,所以共有 43n1 种种植方法,其中包含了 A n与 A 1同种的情况,此时,可以看成 A n和 A 1合为一个区域,则共有 n1 个区域, 学科网（北京）股份有限公司a n1 即 种种植方法, a 43n1a n4 a 3n   a 3n1n4 所以 n n1 ,可得 n n1 ,  a 3nn4 a 34 3 所以,数列 n 是以1为公比的等比数列,又 4 , a 3n 31n4 a 3n31n4n4 所以, n , n . a 12 a 24 2 3 又 , ,也适合上式, a 3n31n4 3n 31n 所以,当 n2 时, n . 5a 53n151n 由分步乘法原理知,在这 n1 个区域上种植花来,不同的种植方法有 n , n2 . （二）数列与概率的交汇 与事件发生次数n（n比较大）有关的概率的计算,通常先确定 与 的递推关系,再构造等差（比）数列 求 . 【例3】（2024届湖南省衡阳市衡阳县第一中学高三下学期最后一卷）在”五四”来临之际,某学校团委组 织以“春风吹,青春启航”为主题的知识竞赛,比赛分初赛和决赛两个阶段,甲、乙两人进入决赛争夺冠军,决 赛规则如下：每轮答题获得 分,其概率为 ,获得 分,其概率为 .最多进行 轮答题,某同学累计得分为 分时,比赛结束,该同学获得冠军,另一同学获得亚军. (1)当进行完 轮答题后,甲同学总分为 ,求 的分布列及 ； (2)若累计得分为 的概率为 ,（初始得分为 分, ） ①求 的表达式( ). ②求获得亚军的概率. 【解析】（1）设进行完 轮答题时,得 分的次数为 , . 学科网（北京）股份有限公司, , 随机变量 表示甲同学的总分,其可能取值为 , , , , , , , 所以 的分布列为： 3 4 5 6 （2）①当 时,即累计得分为 分,是第一轮抢答得 分, ,则 , 累计得分为 分的情况分两种： （i） ,即累计得分为 分,又一轮抢答得 分,其概率为 . （ii） ,即累计得分为 分,又一轮抢答得 分,其概率为 . 则 ,所以 . 所以数列 是首项为 ,公比为 的等比数列. 所以 . ②由①得 , , , , 学科网（北京）股份有限公司各式累加得： . 而 ,所以 . 所以获得冠军的概率： . 所以获得亚军的概率为： . 【例4】马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言 处理、金融领域、天气预测等方面都有着极其广泛的应用．其数学定义为：假设我们的序列状态是…… X ,X ,X ,X X X t2 t1 t t1 t1 t ,…,那么 时刻的状态的条件概率仅依赖前一状态 ,即 PX ,X ,X ,X PX X  t1 t2 t1 t t1 t ． 现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型． 假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为50%,且每局赌赢可以赢得1元,每一局 赌徒赌输的概率为50%,且赌输就要输掉1元．赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游 A  AN*,AB  戏：记赌徒的本金为 一种是赌金达到预期的B元,赌徒停止赌博；另一种是赌徒输光本金 后,赌徒可以向赌场借钱,最多借A元,再次输光后赌场不再借钱给赌徒．赌博过程如图的数轴所示． 当赌徒手中有n元 AnB,nZ 时,最终欠债A元（可以记为该赌徒手中有A元）概率为 P(n) ,请回答 下列问题： P(A) P(B) (1)请直接写出 与 的数值． 学科网（北京）股份有限公司{P(n)} (2)证明 是一个等差数列,并写出公差d． A100 B300,B1500 P(A) P(A) (3)当 时,分别计算 时, 的数值,论述当B持续增大时, 的统计含义． nA A P(A)1 【解析】（1）当 时,赌徒已经欠债 元,因此 ． nB P(B)0 当 时,赌徒到了终止赌博的条件,不再赌了,因此输光的概率 ； （2）记M :赌徒有n元最后输光的事件,N:赌徒有n元上一场赢的事件, 1 1 PMPNPM NP  N  P  M N  ,即P(n) P(n1) P(n1), 2 2 P(n)P(n1)P(n1)P(n) 所以 , {P(n)} 所以 是一个等差数列, P(n)P(n1)d P(n1)P(n2)d, ,P(A1)P(A)d  设 ,则 , 1 累加得 ,故 ,得d  ； P(n)P(A)(nA)d P(B)P(A)(AB)d AB n A （3） ,由（2）P(n)P(A)(n A)d  , A100 AB 2A 2A 代入 可得P(A)P(A) ,即P(A)1 , n A AB AB 1 7 PA P(A) 当 时, ,当 时, , B300 2 B1500 8 P(A) 当B增大时, 也会增大,即输光欠债的可能性越大,因此可知久赌无赢家, 即便是一个这样看似公平的游戏,只要赌徒一直玩下去就会100%的概率输光并负债． （三）数列与立体几何的交汇 求解此类问题,通常先把立体几何知识与排列组合知识结合,然再与与概率与数列等知识建立联系. 【例5】已知正四棱锥 的侧棱和底面边长相等,在这个正四棱锥的 条棱中任取两条,按下列方 式定义随机变量 的值： 若这两条棱所在的直线相交,则 的值是这两条棱所在直线的夹角大小（弧度制）； 学科网（北京）股份有限公司若这两条棱所在的直线平行,则 ； 若这两条棱所在的直线异面,则 的值是这两条棱所在直线所成角的大小(弧度制). （1）求 的值； （2）求随机变量 的分布列及数学期望 . 【解析】根据题意,该四棱锥的四个侧面均为等边三角形,底面为正方形,容易得到 , 为等腰 直角三角形, 的可能取值为： , , ,共 种情况,其中： 时,有 种； 时,有 种； 时,有 种； （1） ； （2） , , 根据（1）的结论,随机变量的分布列如下表： 根据上表, . n4 nN* S n 【例6】（2024届重庆市高三第三次联合诊断）已知 且 ,设 是空间中 个不同的点构成的集合, d S{d |A,BS,AB}. 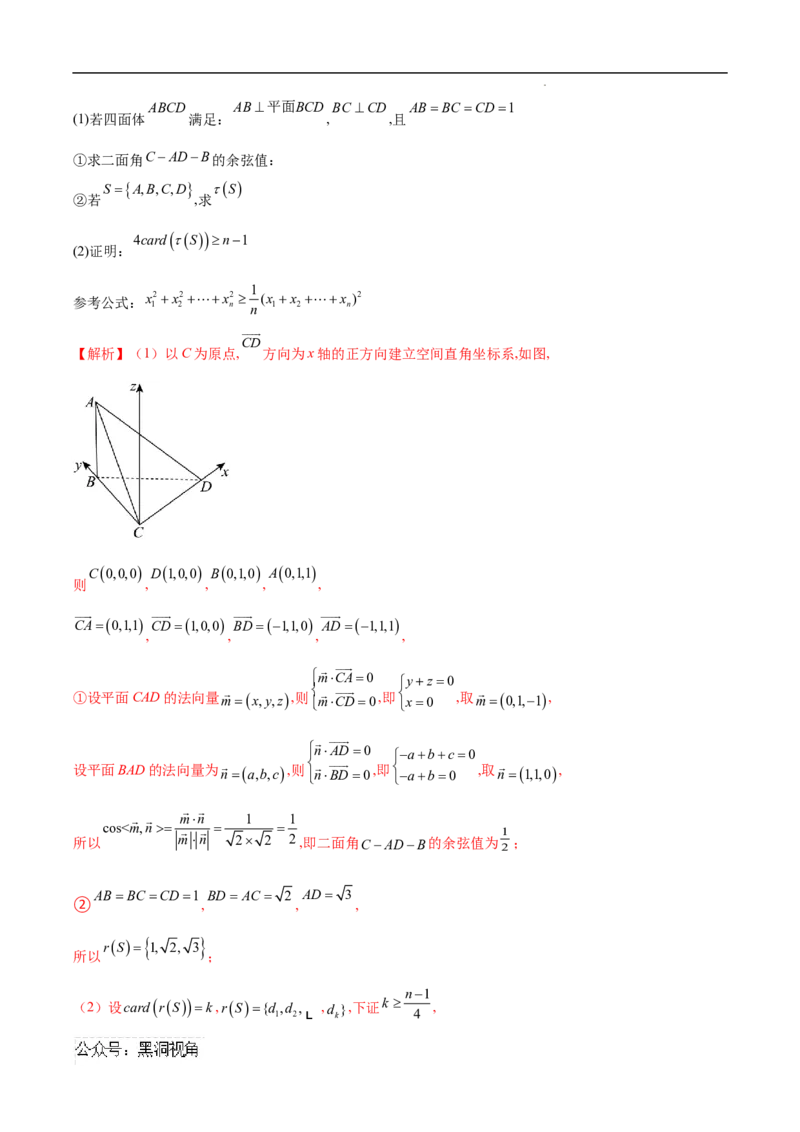其中任意四点不在同一个平面上, AB表示点 A ,B间的距离,记集合 AB 学科网（北京）股份有限公司ABCD AB平面BCD BC CD ABBC CD1 (1)若四面体 满足： , ,且 ①求二面角CADB的余弦值： S A,B,C,D S ②若 ,求 4cardSn1 (2)证明： 1 参考公式：x 1 2x 2 2  x n 2  n (x 1 x 2   x n )2  CD 【解析】（1）以C为原点, 方向为x轴的正方向建立空间直角坐标系,如图, C0,0,0 D1,0,0 B0,1,0 A0,1,1 则 , , , ,     CA0,1,1 CD1,0,0 BD1,1,0 AD1,1,1 , , , , mC  A  0 yz0 ①设平面CAD的法向量m x,y,z,则  mC  D  0 ,即 x0 ,取m 0,1,1,  n  A  D  0 abc0 设平面BAD的法向量为 na,b,c,则  n  B  D  0 ,即 ab0 ,取 n1,1,0, mn 1 1 cos