专题10几何问题_2024-2025高三（6-6月题库）_2024年08月试卷_0816新高考数学题型全归纳之排列组合（20个专题）

专题 10 几何问题 例1．从正方体六个面的对角线中任取两条作为一对．其中所成的角为60的共有( ) A．24对 B．30对 C．48对 D．60对 例2．四面体的一个顶点为A，从其它顶点与各棱的中点中取3个点，使它们和点A在同一平面上，不同的 取法有( ) A．30种 B．33种 C．36种 D．39种 例3．从四面体的顶点及各棱的中点这十个点中，任取3个点确定一个平面，则不同平面个数为( ) A．17 B．23 C．25 D．29 例4．四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，则不同的取法共有( ) A．150种 B．147种 C．144种 D．141种 例5．如果一条直线与一个平面平行，那么称此直线与平面构成一个“平行线面组”，在一个长方体中，由两 个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是( ) A．60 B．48 C．36 D．24 例6．正八边形ABCDEFGH 的8个顶点，以其中3个点为顶点的不同位置的直角三角形共有 个 ． 例7．如图所示，在连接正八边形的三个顶点而成的三角形中，与正八边形有公共边的三角形有多少个． 例8.不共面的四点确定四面体(记得易除共面的情况） (I)以正方体的顶点为顶点,可以确定多少个四面体? （II）以正方体的顶点为顶点,可以确定多少个四棱锥? 例9.考虑44的正方形方格表中的25个格点,则通过至少3个格点有不同直线的数目为 例10.如图，给定由10个点(任意相邻两点距离为1)组成的正三角形点阵，在其中任意取三个点，以这三个 点为顶点构成的正三角形的个数是 12专题 10 几何问题 例1．从正方体六个面的对角线中任取两条作为一对．其中所成的角为60的共有( ) A．24对 B．30对 C．48对 D．60对 【解析】正方体的面对角线共有12条，两条为一对，共有C2 66对， 12 同一面上的对角线不满足题意，对面的面对角线也不满足题意，一组平行平面共有6对不满足题意的直线 对数，不满足题意的共有：3618．从正方体六个面的对角线中任取两条作为一对．其中所成的角为60 的共有：661848．故选：C． 例2．四面体的一个顶点为A，从其它顶点与各棱的中点中取3个点，使它们和点A在同一平面上，不同的 取法有( ) A．30种 B．33种 C．36种 D．39种 【解析】根据题意，如图，分析可得，①所取的3点在3个侧面上时，每个侧面有C3种取法，共3C3 30种 5 5 情况；②所取的3点不在侧面上时，含顶点A的三条棱上各有三个点，它们与所对的棱的中点共面，共有3 种取法；综合可得，共30333种，故选：B． 例3．从四面体的顶点及各棱的中点这十个点中，任取3个点确定一个平面，则不同平面个数为( ) A．17 B．23 C．25 D．29 【解析】考虑点的选择：（1）三个点都是顶点：一共有4种，就是四面体的四个表面；（2）两个顶点，一 个棱中点：为了不和上面的四个面重合，当两个顶点确定时，只有一个选择（此时的面就是一条棱和它的 对棱的中点确定的面），所以这种情况一共有6种；（3）一个顶点，两个棱中点：为了不和上面重合，确定 一个顶点后，则只能选取它的对面的三个中点了，有3种情况，共有4312种；（4）三个都是棱中点： 可以在正四面体中想，这样的面要么和外表面平行要么和一对对棱平行，所以有437种，综上，共有 4612729种．故选：D． 例4．四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，则不同的取法共有( ) A．150种 B．147种 C．144种 D．141种 【解析】从10个点中任取4个点有C4 种取法，其中4点共面的情况有三类．第一类，取出的4个点位于 10 四面体的同一个面上，有4C4种；第二类，取任一条棱上的3个点及该棱对棱的中点，这4点共面，有6 6 种；第三类，由中位线构成的平行四边形（其两组对边分别平行于四面体相对的两条棱），它的4顶点共面， 1有3种．以上三类情况不合要求应减掉，不同的取法共有C4 4C4 63141种．故选：D． 10 6 例5．如果一条直线与一个平面平行，那么称此直线与平面构成一个“平行线面组”，在一个长方体中，由两 个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是( ) A．60 B．48 C．36 D．24 【解析】由题意知本题是一个分类计数问题，一个长方体的面可以和它相对的面上的4条棱和两条对角线 组成6个，一共有6个面，共有6636种结果，长方体的对角面组成两组，共有6个对角面，共有12种 结果，根据分类计数原理知共有361248种结果，故选：B． 例6．正八边形ABCDEFGH 的8个顶点，以其中3个点为顶点的不同位置的直角三角形共有 个． 【解析】正八边形ABCDEFGH 的8个顶点在同一个圆上，8个等分点可得4条直径，可构成直角三角形有 4624个，故答案为： 24 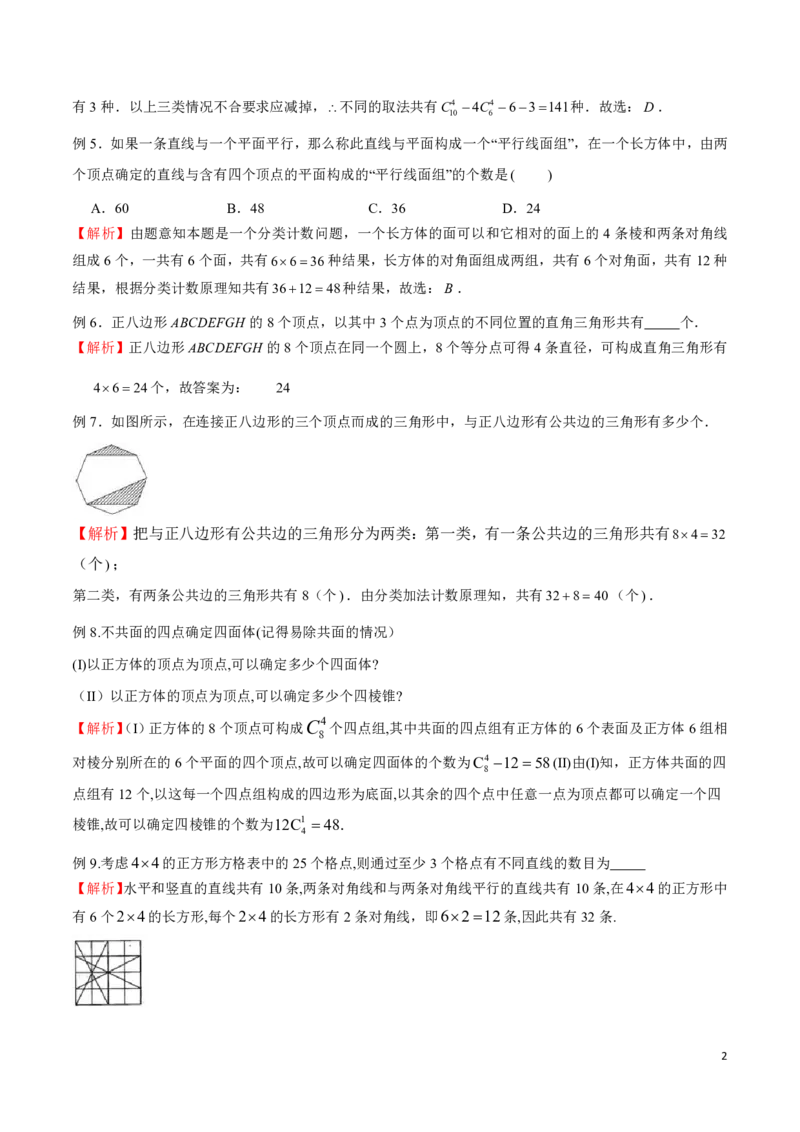例7．如图所示，在连接正八边形的三个顶点而成的三角形中，与正八边形有公共边的三角形有多少个． 【解析】把与正八边形有公共边的三角形分为两类：第一类，有一条公共边的三角形共有8432 （个)； 第二类，有两条公共边的三角形共有8（个)．由分类加法计数原理知，共有32840（个)． 例8.不共面的四点确定四面体(记得易除共面的情况） (I)以正方体的顶点为顶点,可以确定多少个四面体? （II）以正方体的顶点为顶点,可以确定多少个四棱锥? 【解析】（I）正方体的8个顶点可构成C4 个四点组,其中共面的四点组有正方体的6个表面及正方体6组相 8 对棱分别所在的6个平面的四个顶点,故可以确定四面体的个数为C4 1258(II)由(I)知，正方体共面的四 8 点组有12个,以这每一个四点组构成的四边形为底面,以其余的四个点中任意一点为顶点都可以确定一个四 棱锥,故可以确定四棱锥的个数为12C1 48. 4 例9.考虑44的正方形方格表中的25个格点,则通过至少3个格点有不同直线的数目为 【解析】水平和竖直的直线共有10条,两条对角线和与两条对角线平行的直线共有10条,在44的正方形中 有6个24的长方形,每个24的长方形有2条对角线，即6212条,因此共有32条. 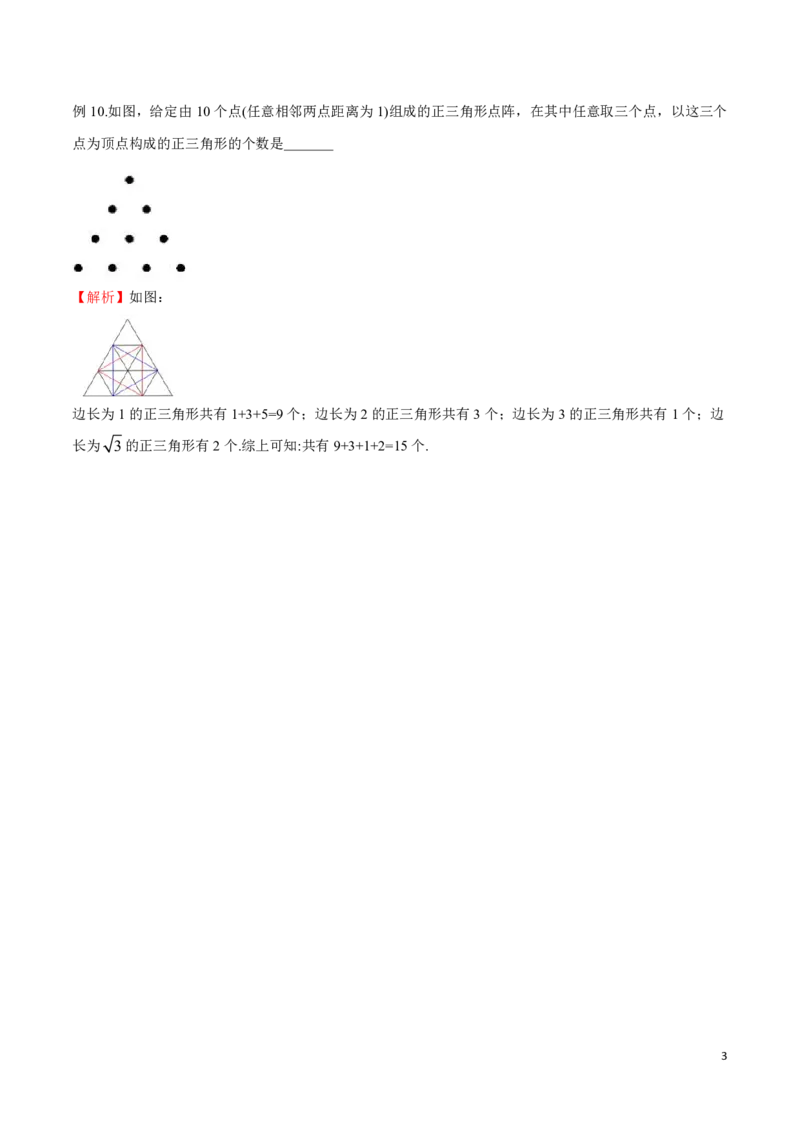2例10.如图，给定由10个点(任意相邻两点距离为1)组成的正三角形点阵，在其中任意取三个点，以这三个 点为顶点构成的正三角形的个数是 【解析】如图： 边长为1的正三角形共有1+3+5=9个；边长为2的正三角形共有3个；边长为3的正三角形共有1个；边 长为 3的正三角形有2个.综上可知:共有9+3+1+2=15个. 34