文档内容
2024-2025 学年安徽省 A10 联盟高二下学期 4 月期中考试
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1. ( )
C3=
7
A. 20 B. 35 C. 120 D. 210
π π
2.已知函数f(x)=cos(2x− ),则f ′(− )=( )
6 3
1
A. −1 B. 0 C. D. 1
2
1
3.已知等差数列{a }的公差d>0,a =3a ,则a + 的最小值为( )
n 5 2 1 d
A. 1 B. √2 C. √3 D. 2
4.用数字1,2,3,4,5组成没有重复数字的四位数,其中偶数的个数为( )
A. 48 B. 60 C. 72 D. 120
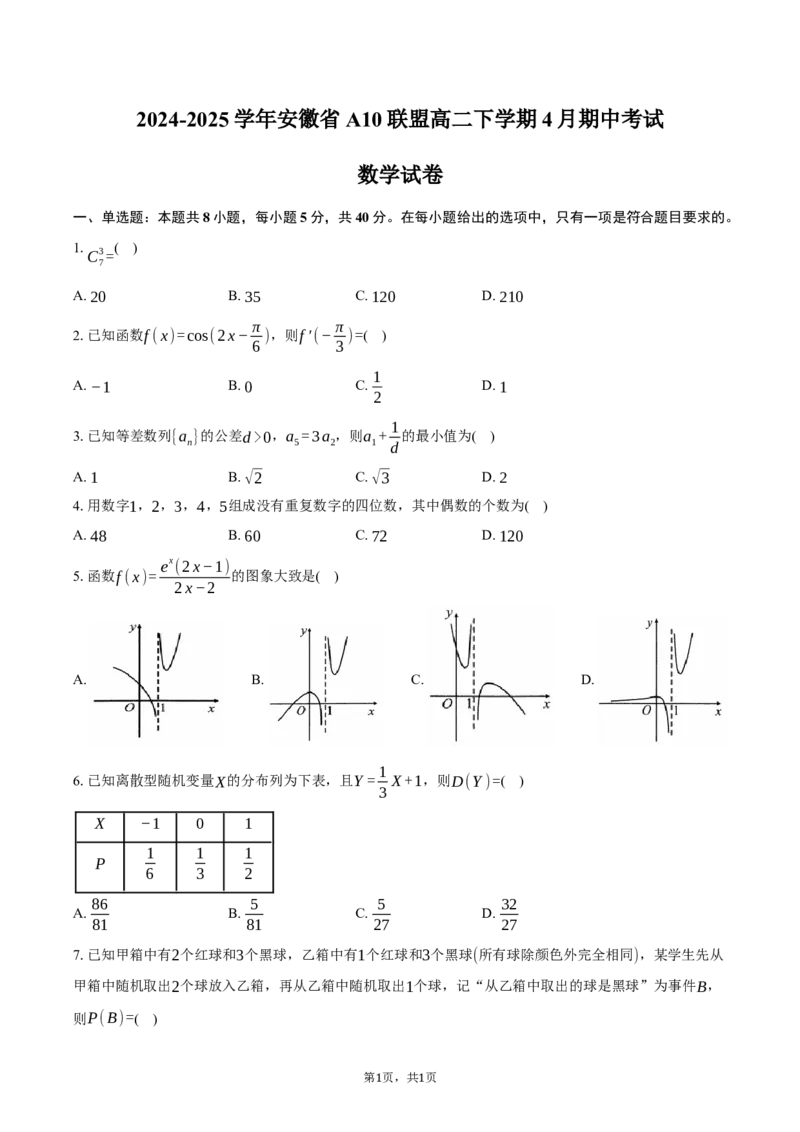
ex (2x−1)
5.函数f(x)= 的图象大致是( )
2x−2
A. B. C. D.
1
6.已知离散型随机变量X的分布列为下表,且Y = X+1,则D(Y)=( )
3
X −1 0 1
1 1 1
P
6 3 2
86 5 5 32
A. B. C. D.
81 81 27 27
7.已知甲箱中有2个红球和3个黑球,乙箱中有1个红球和3个黑球(所有球除颜色外完全相同),某学生先从
甲箱中随机取出2个球放入乙箱,再从乙箱中随机取出1个球,记“从乙箱中取出的球是黑球”为事件B,
则P(B)=( )
第 页,共 页
1 11 1 7 5
A. B. C. D.
14 7 10 18
8.已知函数f(x)=2x+k−xlnx,若f(x)<0对任意x>0恒成立,则实数k的取值范围是( )
A. (−∞,−e) B. (−∞,0) C. (−e,+∞) D. (0,+∞)
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知 ,则下列说法正确的是( )
(1−2x) 2025=a +a x+a x2+⋯+a x2025
0 1 2 2025
A. 展开式中所有项的二项式系数和为22025
B.
a =24C4
4 2025
C. 展开式中系数最大的项为第1350项
32025+1
D. a +a +a +⋯+a =−
1 3 5 2025 2
10.已知m,n为正整数,且m4)
10 10 n n−1 n−1
1
C. (n+1)Am=Am+1 D. Am+1=Am
n n+1 n−m n n
11.对于三次函数 ,给出定义: 是函数 的导数, 是函数
f(x)=ax3+bx2+cx+d(a≠0) f ′(x) f(x) f ″(x)
f ′(x)的导数,若方程f ″(x)=0有实数解x ,则称(x ,f(x ))为函数f(x)的“拐点”.某同学经探究发现:
0 0 0
任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若函数
2 49
f(x)= x3−x2−12x+ ,则下列说法正确的是( )
3 6
137
A. f(x)的极大值为
6
B. f(x)有且仅有2个零点
29
C. 点(2,− )是曲线y=f(x)的对称中心
2
1 2 3 2024
D. f( )+f( )+f( )+⋯+f( )=4048
2025 2025 2025 2025
三、填空题:本题共3小题,每小题5分,共15分。
第 页,共 页
2 112.已知随机变量 的分布规律为 ,则 .
X P(X=i)=ai2 (i=1,2,3) P(X=2)=
1 1 2
13.已知两个随机事件A,B,若P(A)= ,P(B)= ,P(B|A)= ,则P(A|B)= .
5 4 3
14.数列 满足 , ,其中 为函数 的零点,则
{a } a =ea n −2 (n∈N∗) a +a =3x x y=x−2−ln2x(x>1)
n n+1 2 3 0 0
a +a −a = .
1 2 3
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
某社团共有学生9名,其中有5名男生和4名女生,现从中选出4人去参加一项创新大赛.(列式表明计算过程,
结果用数字表示)
(1)如果4人中男生女生各选2人,那么有多少种选法?
(2)如果男生中的甲和女生中的乙必须在内,那么有多少种选法?
(3)如果男生中的甲和女生中的乙至少要有1人在内,那么有多少种选法?
(4)如果4人中必须既有男生又有女生,那么有多少种选法?
16.(本小题15分)
某高中举行爱国主义读书比赛,最终决出一等奖6名同学,其中高一年级2名,高二年级3名,高三年级1名,
现从中任选3人作为代表发言.
(1)求选出的3人中高一年级的人数多于高三年级的人数的概率;
(2)设X表示选出的3人中高二年级的人数,求X的分布列和数学期望.
17.(本小题15分)
1
已知函数f(x)=(x2−2ax)lnx+ x2,a∈R.
2
(1)当a>0时,讨论函数f(x)的单调性;
(2)当x∈[1,+∞)时,函数f(x)有两个零点,求a的取值范围.
18.(本小题17分)
某学校举办趣味投篮比赛,选手需要在距离罚球线1米、2米、3米的A,B,C三个位置分别投篮一次(选
手自行选择投篮顺序),在A,B,C三个位置投篮命中分别可得1分、2分、3分,总分不低于4分就可以获
3 2 1
得奖品.已知甲在A,B,C三处的投篮命中率分别为 , , ,且在这三处的投篮相互独立.
4 3 2
(1)求甲未获得奖品的概率;
(2)在甲获得奖品的情况下,求甲三次投篮都命中的概率;
第 页,共 页
3 1甲参加投篮训练,训练计划如下:在 处先投 个球,若这 个球都投进,则训练结
(3) C n(n∈N∗,n≤60) n
束,否则额外在C处投(200−3n)个球.试问n为何值时,甲投篮次数的期望最大?
19.(本小题17分)
在数列 中,若存在常数 ,使得 恒成立,则称数列 为“ 数列”.
{a } t a =a a ⋯a +t(n∈N∗) {a } H(t)
n n+1 1 2 n n
(1)判断数列1,2,3,7,43是否为“H(1)数列”,并说明理由;
1
(2)若c =1+ ,c =1,试判断数列{c }是否为“H(t)数列”,并说明理由;
n+1 c 1 n
n
n
若数列 为“ 数列”,且 ,数列 为等比数列,且 , ,求
(3) {a } H(t) a =1 {b } ∑a2=a +log b −t t≠0
n 1 n i n+1 3 n
i=1
数列{b }的通项公式.
n
第 页,共 页
4 1参考答案
1.B
2.D
3.B
4.A
5.D
6.B
7.C
8.A
9.ABD
10.CD
11.AD
2
12.
7
7
13.
15
14.−ln2
15.解:(1)如果4人中男生和女生各选2人,
有 种选法;
C2C2=60
5 4
(2)如果男生中的甲与女生中的乙必须在内,
则再从剩下的 人中任选 人,有 种选法;
7 2 C2=21
7
(3)如果男生中的甲与女生中的乙至少要有1人在内,
包含两种情况,
第一种男生中的甲与女生中的乙必须在内有 种,
C2=21
7
第 页,共 页
5 1第二种情况,甲乙仅有一人1人在内,
有 种选法,
C1C3=70
2 7
故有21+70=91种选法;
(4)如果4人中必须既有男生又有女生,
利用间接法,全选后,去掉只有男生和只有女生,
故有 种选法.
C4−C4−C4=120
9 4 5
16.解:(1)记“选出的3人中高一年级的人数多于高三年级的人数”为事件A.
若选出的 人中有高一年级 人,有 种取法
3 1 C1C2 ;
2 3
若选出的 人中有高一年级 人,有 种取法
3 2 C2C1 ;
2 4
所以 P(A)= C1 2 C 3 2+C 2 2C1 4= 1.
C3 2
6
(2)由题意得,X的所有可能取值为0,1,2,3.
P(X=0)= C 3 3 = 1 , P(X=1)= C1 3 C 3 2 = 9 ,
C3 20 C3 20
6 6
P(X=2)= C 3 2C1 3= 9 , P(X=3)= C 3 3 = 1 .
C3 20 C3 20
6 6
所以X的分布列为:
1 9 9 1 3
所以E(X)=0× +1× +2× +3× = .
20 20 20 20 2
第 页,共 页
6 117.解:(1)函数f(x)的定义域为(0,+∞),
f ′(x)=(2x−2a)(lnx+1)=2(x−a)(lnx+1),
1
令f ′(x)=0,解得x =a,x = .
1 2 e
1 1 1
当00,x∈(a, ),f ′(x)<0,x∈( ,+∞),f ′(x)>0,
e e e
1 1
∴f(x)的单调递增区间为(0,a)和( ,+∞),f(x)的单调递减区间为(a, );
e e
1
当a= 时,f ′(x)≥0恒成立,∴f(x)在(0,+∞)上单调递增;
e
1 1 1
当a> 时,∵x∈(0, ),f ′(x)>0,x∈( ,a),f ′(x)<0,x∈(a,+∞),f ′(x)>0,
e e e
1 1
∴f(x)的单调递增区间为(0, )和(a,+∞),f(x)的单调递减区间为( ,a).
e e
(2)f ′(x)=2(x−a)(lnx+1),x∈[1,+∞).
当a≤1时,f ′(x)≥0,则f(x)在[1,+∞)上单调递增,
1
∴f(x)≥f(1),即f(x)≥ ,函数f(x)在[1,+∞)上没有零点.
2
当a>1时,x∈(1,a),f ′(x)<0;x∈(a,+∞),f ′(x)>0,
∴f(x)在(1,a)上单调递减,在(a,+∞)上单调递增,
1
∵f(1)= >0,f(2a)=2a2>0,
2
要使得f(x)在[1,+∞)上有两个零点,只需f(x) =f(a)<0,
min
1
∴a2 (−lna+ )<0,解得a>√e.
2
综上,a的取值范围为(√e,+∞).
3 2 1 1
18.解:(1)甲三次投篮都命中的概率P = × × = ,
1 4 3 2 4
甲三次投篮只命中两次且总分不低于 分的概率 ( 3) 2 1 3 ( 2) 1 5 ,
4 P = 1− × × + × 1− × =
2 4 3 2 4 3 2 24
第 页,共 页
7 113
所以甲未获得奖品的概率为P=1−P −P = .
1 2 24
(2)记“甲获得奖品”为事件A,“甲三次投篮都命中”为事件B.
1
P(AB) 4 6
在甲获得奖品的情况下,甲三次投篮都命中的概率为P(B|A)= = = .
P(A) 11 11
24
(3)设甲的投篮次数为X,则X的分布列为
200−2n
X n
1 1
1−
P 2n 2n
则 n ( 1 ) 3n−200 .
E(X)= +(200−2n)× 1− = −2n+200
2n 2n 2n
3n−200 3n−197
令f(n)= −2n+200(n∈N ),则f(n+1)= −2n+198,
2n + 2n+1
203−3n−2n+2
,当 时, ,当 时 ,
f(n+1)−f(n)= n≤5 f(n+1)>f(n) n≥6 f(n+1)f(7)>f(8)> ⋯,
故当n=6时,甲投篮次数的期望最大.
19.解:(1)由题意得,2=1+1,3=1×2+1,7=1×2×3+1,43=1×2×3×7+1,则1,2,3,7,
43是“H(1)数列”;
1 3
(2)由c =1,c =1+ ,得c =2,c = ,
1 n+1 c 2 3 2
n
由c =c +t,得t=1,
2 1
∴c ≠c c +1,∴{c }不是“H(t)数列”.
3 1 2 n
(3)设数列{b }的公比为q,
n
由a =a a ⋯a +t,n=1,得a =a +t=1+t,
n+1 1 2 n 2 1
n
由 , ,得 ,
∑a2=a +log b −t n=1 a2=a +log b −t
i n+1 3 n 1 2 3 1
i=1
∴1=1+t+log b −t,解得b =1.
3 1 1
第 页,共 页
8 1由 ,得 , ,
a =a a ⋯a +t a =a a +t=1+2t a =a a a +t=2t2+4t+1
n+1 1 2 n 3 1 2 4 1 2 3
n
由 ,得 ,
∑a2=a +log b −t a2+a2=a +log b −t
i n+1 3 n 1 2 3 3 2
i=1
,
∴1+(1+t) 2=1+2t−t+log b
3 2
,
∴log b =1+t+t2
3 2
.
∴log q=1+t+t2
3
n
由 ,得 ,
∑a2=a +log b −t a2+a2+a2=a +log b −t=a +log q2−t
i n+1 3 n 1 2 3 4 3 3 4 3
i=1
则 ,
1+(1+t) 2+(1+2t) 2=2t2+4t+1+2(1+t+t2 )−t
解得t=−1,
, , , .
∴log q=1 ∴q=3 ∵b =1 ∴b =3n−1
3 1 n
第 页,共 页
9 1