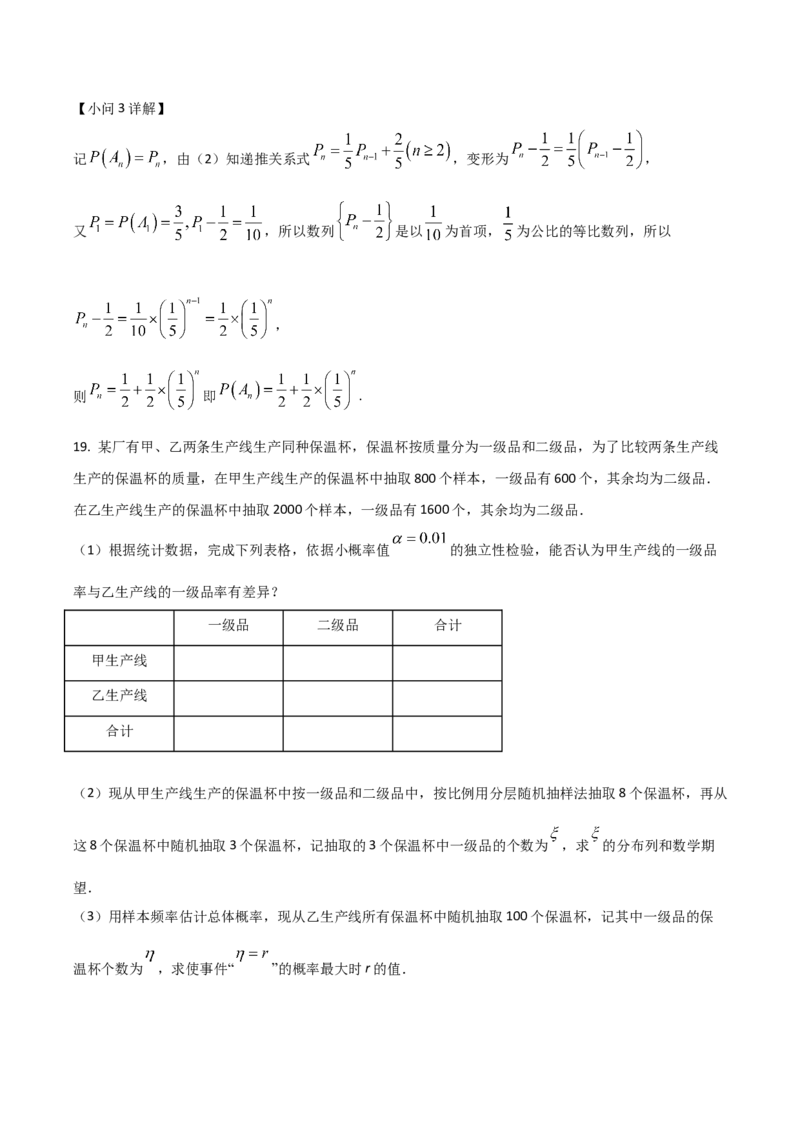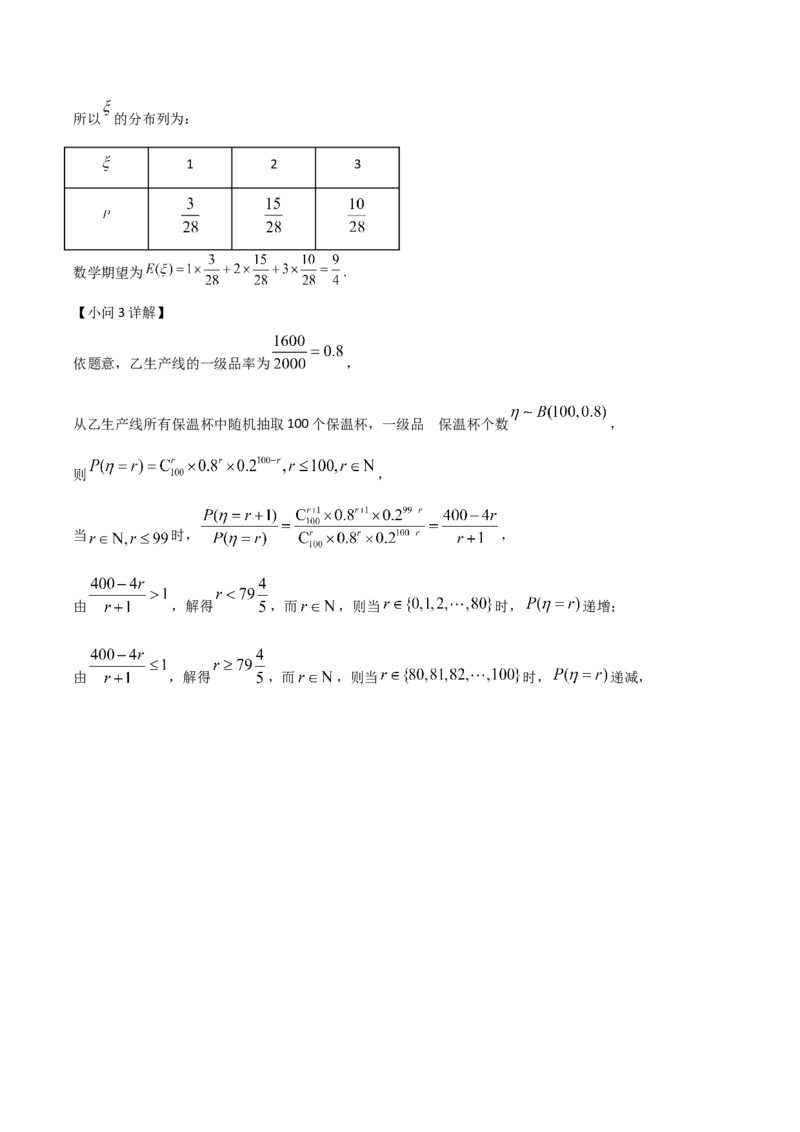文档内容
山东名校考试联盟
2024-2025 学年高二年级下学期期中检测
数 学 试 题
2025.04
本试卷共4页,19题,全卷满分150分.考试用时120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 集合 , ,则 ( )
A. B. C. D.
【答案】D
【详解】 ,
故选:D.
2. 的展开式中的常数项为( )
A. 30 B. 45 C. 60 D. 75
【答案】A
【详解】 展开式的通项公式为 ,
令 , ,展开式的常数项为 .故选:A.
3. 一袋中有外观完全相同,标号分别为1,2,3,4,5的五个球,现在分两次从中有放回地任取一个球,
设事件 “第一次取得5号球”,事件 “第二次取得5号球”,则 ( )
A. B. C. D.
【答案】B
【详解】依题意, ,
所以 .
故选:B
4. 已知命题 ,则 为( )
A. B.
C. D.
【答案】A
【详解】全称量词命题的否定为存在量词命题,
所以 为“ ”.
故选:A.
5. 现有6种不同的颜色给图中的四块区域涂色,若每个区域涂一种颜色,相邻区域不能涂同一种颜色,则
不同的涂法共有( )
A. 400种 B. 460种 C. 480种 D. 496种
【答案】C【详解】当使用4种颜色时,不同的涂法有 种方法;
当使用3种颜色时,不同的涂法有 种方法;
所以不同的涂法共有 种.
故选:C.
6. 已知变量 线性相关,其一组样本数据 ,满足 ,用最小二乘法得到
的经验回归方程为 .若增加一个数据 后,得到修正后的回归直线的斜率为2.1,则数据
的残差的绝对值为( )
A 0.1 B. 0.2 C. 0.3 D. 0.4
【答案】A
【详解】由题设 ,则 ,
增加数据 后, , ,且回归直线为 ,
所以 ,则 ,
所以 ,有 ,故残差的绝对值为 .
故选:A
7. 甲、乙两人玩掷骰子游戏,每局两人各随机掷一次骰子,当两人的点数之差为偶数时.视为平局,当两
人的点数之差为奇数时,谁的骰子点数大该局谁胜.重复上面的步骤,游戏进行到一方比另一方多胜2局
或平局4次时停止,记游戏停止时局数为X次,则 ( )
A. B. C. D.
【答案】D【详解】甲乙每次掷股子1次,若两人的点数都是偶数或都是奇数,则平局,所以平局的概率
,
若甲胜,则结果有 , , , , , , , , ,9种,
所以甲胜的概率为 ,同理乙胜的概率也为 ,
局数为4次后停止游戏,若4次全平局,概率为 ;
若平局2次,则最后1次不能是平局,
另外2次甲全胜或乙全胜,概率为 ,
若平局0次,则一方3胜1负,且负的1次只能在前2次中,
概率为 ,
所以 .
故选:D.
8. 今有A、B、C、D、E、F共6本不同的书全部分给4个同学,每个同学至少分到一本,其中A、B必须分
给同一个同学的概率为( )
A. B. C. D.
【答案】A
【详解】将这6本不同的书分成四组,再分配到不同的同学,
若书的个数为3,1,1,1,则不同的安排方法种数为: 种;
若书的个数为2,2,1,1,则不同的安排方法种数为: 种,故不同的安排方法共有 种.
将这6本不同的书分成四组,再分配到不同的同学,A,B分给同一个同学,
若书的个数为3,1,1,1,则不同的安排方法种数为: 种;
若书的个数为2,2,1,1,则不同的安排方法种数为: 种,
故不同的安排方法共有 种.
所以所求事件的概率为 .
故选:A.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 设 ,满足 ,则下列结论正确的是( )
A. 的最大值为 B. 的最小值为4
C. 的最大值为2 D. 的最小值为4
【答案】BD
【详解】由 , 得: ,当且仅当 时,等号成立,故A不正
确.
,当且仅当 时,等号成立,故B正确.
,即 ,故C不正确.
,当且仅当 时,等号成立,故D正确.
故选:BD.10. 已知随机变量 服从正态分布 ,且 ,任取3个随机变量 ,记 在区间
的个数为X,则正确的有( )
A. B.
C. D.
【答案】AB
【详解】对于A,由 ,得 ,
则 ,A正确;
对于B,由A知, 在区间 的概率为 ,
因此 ,B正确;
对于C,由B知, ,
因此 ,C错误;
对于D, ,D错误.
故选:AB
11. 有一组成对样本数据 , , , ,设 , ,由这组数据
得到新成对样本数据 ,下面就这两组数据分别先计算
样本相关系数,再根据最小二乘法计算经验回归直线,最后计算出残差平方和,则( )
附:回归直线的斜率和截距的最小二乘估计公式分别为: , .相关系数.
A. 两组数据的相关系数相同 B. 两组数据的残差平方和相同
C. 两条经验回归直线的斜率相同 D. 两条经验回归直线的截距相同
【答案】ABC
【详解】由于新成对样本数据 ,
其平均数分别为 ,
同理 ,
这样根据公式 ,
用样本数据减去平均数得 与新成对数据 ,
用样本数据减去平均数得 与新成对数据 ,
即它们每一个对应数据的差值都是一样的,
这就说明两条经验回归直线的斜率相同,两组数据的相关系数相同, 故A、C正确;
由于回归直线经过样本数据的样本点为 ,而新数据的样本点为 ,
即样本数据的回归直线方程为 ,而新数据的回归直线方程为 ,
故两条经验回归直线的截距不相同,故D错误;
由于样本数据回归直线和新数据回归直线是平行关系,所以实际值与估计值的差的平方和应该是相同的,
即两组数据的残差平方和相同,故B正确;
故选:ABC.
三、填空题:本题共3小题,每小题5分,共15分.12. 设随机变量 ,则 的最大值为__________.
【答案】1
【详解】因为随机变量 , ,
当且仅当 时等号成立,所以 的最大值为1.
故答案为:1.
13. 为了调查A,B两个地区的观众是否喜欢娱乐节目M,某电视台随机调查了A,B两个地区的2x名观众,
已知从A,B两个地区随机调查的人数相同,A地区喜欢娱乐节目M的人数占A地区参与调查的总人数的
,B地区喜欢娱乐节目M的人数占B地区参与调查的总人数的 ,若根据独立性检验认为喜欢娱乐节目
M和地区有关,且此推断犯错误的概率超过0.01但不超过0.05,则所有x构成的集合为__________.
附表: ,其中 .
0.050 0.010
3.841 6.635
【答案】
【详解】 列联表为:
喜欢 不喜欢 合计
A地区
B地区
合计,
由认为喜欢娱乐节目M和地区有关,且此推断犯错误的概率超过0.01但不超过0.05,
得 ,则 ,解得 ,又 是5的倍数,
则 可以取的值为 ,所以x构成的集合为 .
故答案为:
14. a,b,c都为正整数, ,随机变量 ,则 __________.
【答案】3.8
【详解】 ,且 ,将7个小球排成一列形成6个间隙,
用2块隔板将7个小球分成3部分,每部分小球数即为 , , 的取值,
因此 , , 的取值共有 种情况, 的所有可能取值为3,4,5,
当 时, , , 的取值有两种情况:
① , , 中有一个是3,余下两个都为2,则有 种情况,
② , , 中有二个是3,余下一个为1,则有 种情况,则 ;
当 时,即 , , 中有一个是4,余下两个分别为1,2,则有 种情况, ;
当 时,即 , , 中有一个是5,余下两个都是1,则有 种情况, ;
所以 .
故答案为:四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
的
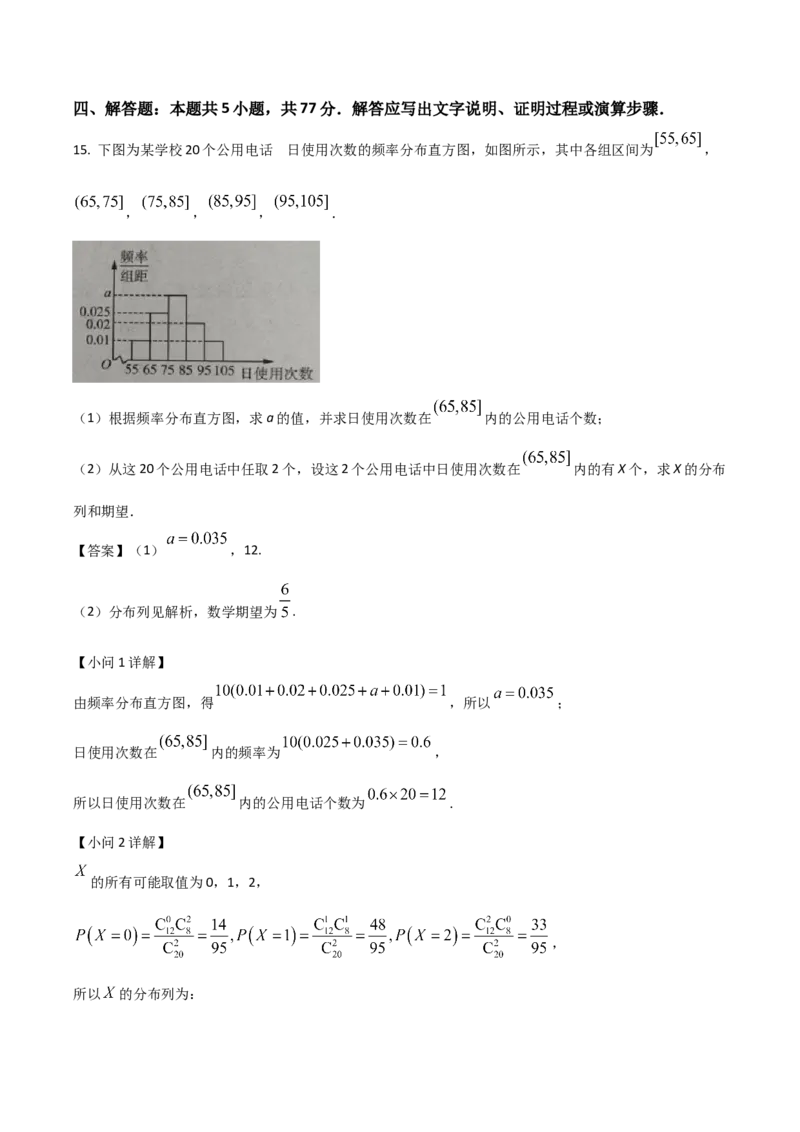
15. 下图为某学校20个公用电话 日使用次数的频率分布直方图,如图所示,其中各组区间为 ,
, , , .
(1)根据频率分布直方图,求a的值,并求日使用次数在 内的公用电话个数;
(2)从这20个公用电话中任取2个,设这2个公用电话中日使用次数在 内的有X个,求X的分布
列和期望.
【答案】(1) ,12.
(2)分布列见解析,数学期望为 .
【小问1详解】
由频率分布直方图,得 ,所以 ;
日使用次数在 内的频率为 ,
所以日使用次数在 内的公用电话个数为 .
【小问2详解】
的所有可能取值为0,1,2,
,
所以 的分布列为:0 1 2
数学期望 .
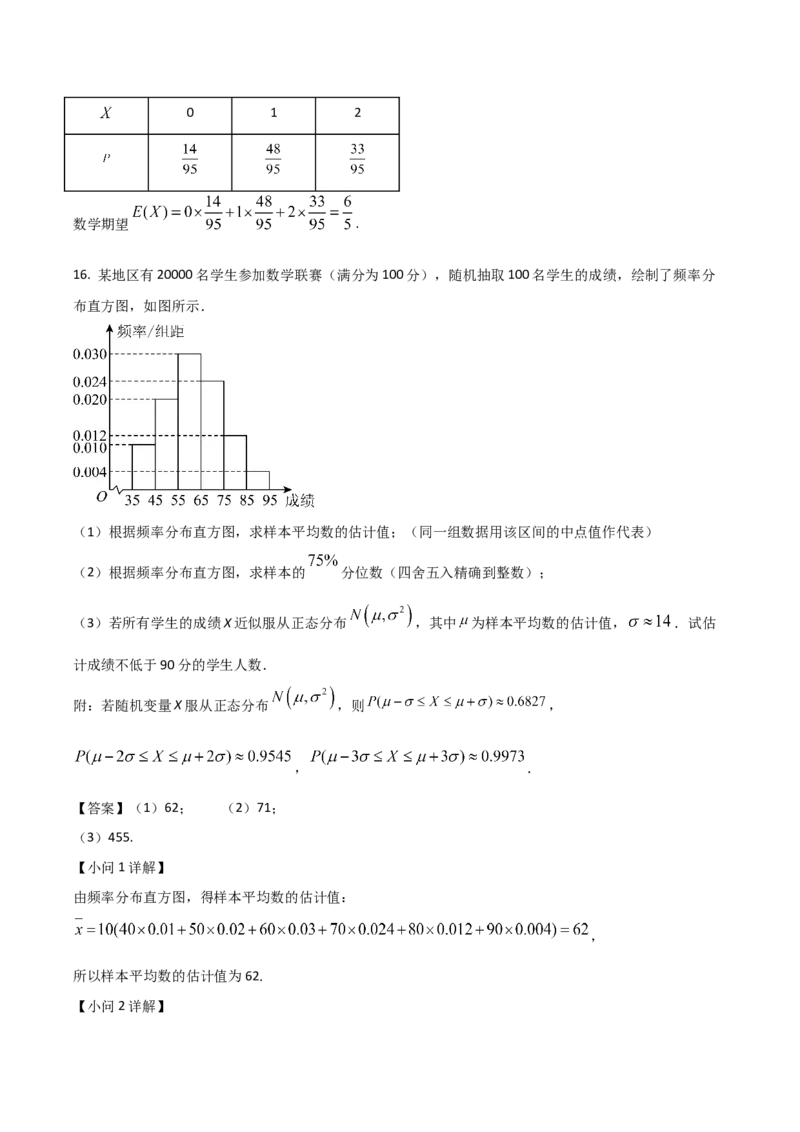
16. 某地区有20000名学生参加数学联赛(满分为100分),随机抽取100名学生的成绩,绘制了频率分
布直方图,如图所示.
(1)根据频率分布直方图,求样本平均数的估计值;(同一组数据用该区间的中点值作代表)
(2)根据频率分布直方图,求样本的 分位数(四舍五入精确到整数);
(3)若所有学生的成绩X近似服从正态分布 ,其中 为样本平均数的估计值, .试估
计成绩不低于90分的学生人数.
附:若随机变量X服从正态分布 ,则 ,
, .
【答案】(1)62; (2)71;
(3)455.
【小问1详解】
由频率分布直方图,得样本平均数的估计值:
,
所以样本平均数的估计值为62.
【小问2详解】由频率分布直方图知,前3组的频率和为 ,第4组的频率为0.24,
所以样本的 分位数为 .
【小问3详解】
由(1)知,样本平均数的估计值 ,则 ,
因此 ,
所以成绩不低于90分的学生人数约为 .
17. 某景区经过提质改造后统计连续5天进入该景区参观的人数(单位:千人)如下:
日期 3月5日 3月6日 3月7日 3月8日 3月9日
第x天 1 2 3 4 5
参观人数y 2.2 2.6 3.1 5.2 6.9
(1)建立 关于 的回归直线方程,预测第10天进入该景区参观的人数;
(2)该景区只开放东门,西门供游客出入,游客从东门,西门进入该景区的概率分别为 、 ,且出景
区与进入景区选择相同的门的概率为 ,出景区与进入景区选择不同的门的概率为 .假设游客从东门,
西门出入景区互不影响,求甲,乙两名游客都从西门出景区的概率.
附:参考数据: .
参考公式:回归直线方程 ,其中 , .【答案】(1) ,约为 千人;
(2) .
【小问1详解】
依题意, ,而 ,
则 , ,
因此 ,当 时, ,
所以 关于 的回归直线方程为 ,第10天进入该景区参观的人数约为 千人.
【小问2详解】
记“甲从西门进入景区”为事件 ,“甲从西门出景区”为事件 ,“乙从西门出景区”为事件 ,
, ,
由全概率公式得 ,同理 ,
所以甲,乙两名游客都从西门出景区的概率 .
18. 有 个编号分别是 的不透明的罐子里装有除颜色外完全相同的糖果.第1个罐子中装有3颗红
色糖果和2颗绿色糖果,其余罐子中都装有2颗红色糖果和2颗绿色糖果.现先从第1个罐子中随机取出一
颗糖果放入第2个罐子,再从第2个罐子中随机取出一颗糖果放入第3个罐子,依此类推,直至从第 个
罐子中随机取出一颗糖果.设事件 表示从第 个罐子中取出红色糖果,记事件 发生的概率为 .
(1)求 的值;
(2)求 的值,并证明:当 时, ;
(3)求 (用含 的式子表达).
【答案】(1) ;
(2) ,证明见解析;
(3) .
【小问1详解】
在第一个罐子中共有糖果 颗,其中红色糖果有3颗,根据古典概型概率公式,
【小问2详解】
由(1)知, ,
所以 ,
当 时,由全概率公式,得
所以 即 ;【小问3详解】
记 ,由(2)知递推关系式 ,变形为 ,
又 ,所以数列 是以 为首项, 为公比的等比数列,所以
,
则 即 .
19. 某厂有甲、乙两条生产线生产同种保温杯,保温杯按质量分为一级品和二级品,为了比较两条生产线
生产的保温杯的质量,在甲生产线生产的保温杯中抽取800个样本,一级品有600个,其余均为二级品.
在乙生产线生产的保温杯中抽取2000个样本,一级品有1600个,其余均为二级品.
(1)根据统计数据,完成下列表格,依据小概率值 的独立性检验,能否认为甲生产线的一级品
率与乙生产线的一级品率有差异?
一级品 二级品 合计
甲生产线
乙生产线
合计
(2)现从甲生产线生产的保温杯中按一级品和二级品中,按比例用分层随机抽样法抽取8个保温杯,再从
这8个保温杯中随机抽取3个保温杯,记抽取的3个保温杯中一级品的个数为 ,求 的分布列和数学期
望.
(3)用样本频率估计总体概率,现从乙生产线所有保温杯中随机抽取100个保温杯,记其中一级品的保
温杯个数为 ,求使事件“ ”的概率最大时r的值.附: ,其中 .
0.1 0.05 0.01 0.005
2.706 3.841 6.635 7.879
【答案】(1)列联表见解析,能;
(2)分布列见解析,数学期望为
(3)80.
【小问1详解】
依题意, 列联表如下:
一级品 二级品 合计
甲生产线 600 200 800
乙生产线 1600 400 2000
合计 2200 600 2800
零假设 :甲生产线的一级品率与乙生产线的一级品率无差异,
根据列联表中数据,经计算得 ,
所以依据小概率值 的独立性检验,推断 不成立,
即认为甲生产线的一级品率与乙生产线的一级品率有差异,此推断犯错误的概率不大于0.01.
【小问2详解】
依题意,用分层随机抽样法抽取的8个保温杯中,一级品保温杯有 个,二级品有2个,
随机变量 的可能值为1,2,3,
,所以 的分布列为:
1 2 3
数学期望为 .
【小问3详解】
依题意,乙生产线的一级品率为 ,
的
从乙生产线所有保温杯中随机抽取100个保温杯,一级品 保温杯个数 ,
则 ,
当 时, ,
由 ,解得 ,而 ,则当 时, 递增;
由 ,解得 ,而 ,则当 时, 递减,