文档内容
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}2023~2024 学年福州市高三年级 4 月份质量检测
参考答案与评分细则
一、选择题:本大题考查基础知识和基本运算.每小题5分,满分40分.
1.D 2.C 3 .A 4.C 5.D 6 .B 7.B 8.A
二、选择题:本大题考查基础知识和基本运算.每小题 6 分,满分 18 分.全部
选对的得6分,部分选对的得部分分,有选错的得 0分.
9.ABC 10.BC 11 .ACD
三、填空题:本大题考查基础知识和基本运算.每小题5分,满分15分.
12.- 2 13 .8 14.6,22
四、解答题:本大题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演
算步骤.
15. 【考查意图】本小题主要考查递推数列与数列求和等基础知识,考查运算求解能力、推
理论证能力等;考查分类与整合、化归与转化等思想方法;考查数学运算、逻辑推理等核心
素养;体现基础性和综合性.满分13分.
解:(1)因为aan=n +2, 2 ,所以aa- =n 2 ,···································1分
n n- 1 … n n- 1
当n 2时,aaa=a-(a)a()a( +-++a- ) + L ,
… nnnn n -- 11221 - 1
所以an=22n2+4-++2 + L ,·························································3分
n
n(22+)n
所以a = ,n 2,所以a =nn2 +n , 2, ··································4分
n 2 … n …
又因为a =2,···············································································5分
1
所以ann=+n2 Î , N*.······································································6分
n
(2)由(1)可知ann=n+n=2+ nÎ (1), N*,·············································7分
n
111 1
所以 == - ,····························································9分
annn ( n+1 ) +1
n
111 1
所以S =+++ +L
n 12´´- 23(1)(1) + nnn n
111111 1
=-1 +-++- + - L ,·····································11分
2231 nn- n1 n +
1
所以S =1- ,·········································································12分
n n+1
又因为n 1,所以S <1.·································································································13分
… n
参考答案 第 1 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}16.【考查意图】本小题主要考查正态分布、全概率公式、条件概率等基础知识,考查数学
建模能力、逻辑思维能力和运算求解能力等,考查分类与整合思想、概率与统计思想等,考
查数学建模、数据分析、数学运算等核心素养,体现基础性、综合性和应用性.满分15分.
解:(1)依题意得,m=0,0s.2= ,···························································1分
所以零件为合格品的概率为PX(0-==, m n = .
m n 5´ 1 5
参考答案 第 3 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}2 5
所以平面DBP与平面BPA夹角的余弦值为 .····································15分
5
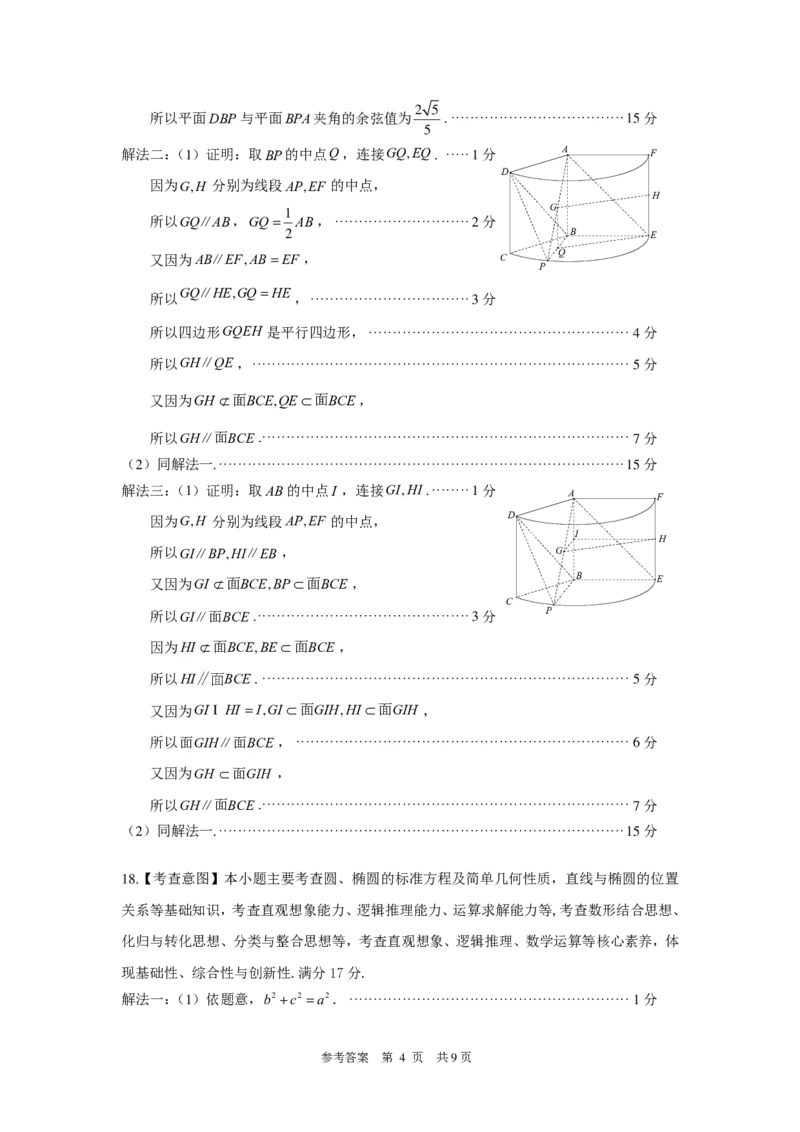
解法二:(1)证明:取BP的中点Q,连接GQE, Q . ·····1分 A F
D
因为G,H 分别为线段APE, F 的中点,
H
G
1
所以GQ∥AB ,GQA=B ,····························2分
2 B E
又因为AB∥EFAB,EF = , C Q
P
GQ∥HEGQ,HE=
所以 ,·································3分
所以四边形GQEH 是平行四边形,······················································4分
所以GHQ∥E ,··············································································5分
又因为GHBË C面EQEBC,EÌ 面 ,
所以GHB∥C面E .············································································7分
(2)同解法一.····················································································15分
解法三:(1)证明:取AB的中点I ,连接GIH, I .········1分
A F
D
因为G,H 分别为线段APE, F 的中点,
I
H
所以GIB∥PHIE, B∥ , G
又因为GIBËC面EBPBC,E Ì 面 , B E
C
所以GIB∥C面E .············································3分 P
因为HIBË C面EBEBC,E Ì 面 ,
所以HIB∥C面E .············································································5分
又因为GIHIIIGIG=ÌIH,HIGIH面 Ì , 面 ,
所以面GIHB∥C面E ,·····································································6分
又因为GHGÌ IH面 ,
所以GHB∥C面E .············································································7分
(2)同解法一.····················································································15分
18.【考查意图】本小题主要考查圆、椭圆的标准方程及简单几何性质,直线与椭圆的位置
关系等基础知识,考査直观想象能力、逻辑推理能力、运算求解能力等,考查数形结合思想、
化归与转化思想、分类与整合思想等,考査直观想象、逻辑推理、数学运算等核心素养,体
现基础性、综合性与创新性.满分17分.
解法一:(1)依题意,bc22+ a2= .··························································1分
参考答案 第 4 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}x 2 y 2
设Px(, y) ,则 0 + 0 =1,-c,所以a> x , >x ,所以|PFa|= -x ,d = - x
a 0 c 0 2 a 0 c 0
c
a- x
所以 |PF 2 | = a 0 = c ,即 |PF 2 | 为定值,且这个定值为 c . ··················4分
d a2 a d a
- x
c 0
x y
(2)(ⅰ)依题意,G(, 0 ) 0 ,
3 3
x
设直线IG与x轴交于点C,因为IG⊥x轴,所以C(,00) ,·······················5分
3
x x 2
所以|||F|(C)(FC-=c+c )-- =0 x 0 ,··········································6分
12 33 3 0
因为△PF F 的内切圆与x轴切于点C,
1 2
2
所以|||P|||F|PF-=F- |CFC= x ,·················································7分
1212 0 3
又因为|||P|F2PF+ a= ,
1 2
x y
解得|PF |=a- 0 ,·········································· 8分
2 3
P
c
由(1)得|PFa|= -x ,
2 a 0 G
I
所以ax-= c -a x 0 , F1 O C F2 x
a 0 3
c 1
所以椭圆E的离心率e= = .·························10分
a 3
c 1
(ⅱ)由2a=6,得a=3,又 = ,所以c=1,ba22=- c2= 8,
a 3
x2 y2
所以椭圆E的方程为 + =1.······················································11分
9 8
根据椭圆对称性,不妨设点P在第一象限或y轴正半轴上,即0 x <3,02< y2 ,
„ 0 0„
又F(1- ,0) ,F (1,0),
1 2
y
所以直线PF 的方程为y= 0 (1x)+ ,
1 x +1
0
x y (3x) +
设直线IG与PF 交于点D,因为x = 0 ,所以y = 0 0 ,
1 D 3 D 3(1x) +
0
△F CD的面积S 与△PF F 的面积S之比为
1 1 1 2
1 xy x (3) +
(1)00+ 0 ´
S 233(1)(3) x + x + 2
1 = 0 = 0 ,················································13分
S 1 ´ 2´ y 18(1x) 0 +
2 0
(3x)+ 2 (3x)+(1) x-
令 f(x)= (0 x<3),则 f ¢ (x)= ,
18(1x)+ „ 18(x+1)2
参考答案 第 5 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}当xÎ [0,1), f ¢ ()x <0 ,当xÎ (1,3), f ¢ ()x >0 ,
所以函数 f(x)在[0,1)单调递减,在(1,3)单调递增.
1 4 1
又因为 f(0)= , f(1)= , f(3)= ,
2 9 2
4 1
所以 f(x)的值域是[, ] ,
9 2
4 S 1
所以 1 ,··········································································15分
„ „
9 S 2
4 S
所以 1 1,·······································································16分
5„ S - S „
1
根据对称性,
4 5
△PF F 被直线IG分成两个部分的图形面积之比的取值范围是[, ] .········17分
1 2
5 4
解法二:(1)同解法一···········································································4分
x y
(2)(ⅰ)依题意,G(, 0 ) 0 ,
3 3
x
设直线IG与x轴交于点C,因为IG⊥x轴,所以C(,00) ,·······················5分
3
x x 2
所以|||F|(C)(FC-=c+c )-- =0 x 0 ,··········································6分
12 33 3 0
因为△PF F 的内切圆与x轴切于点C,
1 2
2
所以|||P|||F|PF-=F- |CFC= x ,·················································7分
1212 0 3
ì x
ï ||PF =a+, 0
ï 1 3
又因为|||P|F2PF+ a= ,得í ···········································8分
1 2 ï x
||PF =a.- 0
ïî 2 3
ì x
ï ()xcy++=2a+ 2 , 0
所以 ï í 0 0 3 两式平方后取差,得4cxax= 4 对任意x 成立,
ï x 0 3 0 0
()xcy-+= 2-a 2 , 0
ïî 0 0 3
c 1
所以椭圆E的离心率e= = .························································10分
a 3
(ⅱ)同解法一···················································································17分
解法三:(1)同解法一···········································································4分
x y x
(2)(ⅰ)依题意,G(, 0 ) 0 ,因为IG⊥x轴,设点I坐标为(, 0) t .··········5分
3 3 3
y
可求直线PF方程为yx= c 0 ( + ),
1 x +c
0
x
yc(tx)(0 +c- ) +
0 3 0
则点I到直线PF的距离 =|t|,·································6分
1 yx2 +(c + )2
0 0
æ x ö 2 ( )
即ç yc(tx)(c0)t(y+x-+=+c) + ÷ 22 2 ,化简得
è 0003 0 ø
x x
yttc2x+c+y2+()-+()0() c= 0 0 2 ,①
00 30 3
同理,由点I到直线PF 的距离等于|t|,可得
2
参考答案 第 6 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}x x
yttc2x+c----y2()(=)0() c 0 0 2 ,②············································7分
00 30 3
8 4 y
将式①- 式②,得2tc×x=ycx × ,则t = 0 .·····································8分
3 00 03 4
y
将t = 0 代入式①,得
4
yx2 1 x
00+++(-+)()() c=xc0 0 c 2 ,
1623 0 3
x2 y2
化简得 0 + 0 =1,
9c2 8c2
得9c2 =a2,
c 1
所以椭圆E的离心率e= = .························································10分
a 3
(ⅱ)同解法一···················································································17分
19.【考查意图】本小题主要考查集合、导数、不等式等基础知识,考查逻辑推理能力、直
观想象能力、运算求解能力和创新能力等,考查函数与方程思想、化归与转化思想、分类与
整合思想、数形结合思想等,考查数学抽象、逻辑推理、直观想象、数学运算等核心素养,
体现基础性、 综合性与创新性.满分17分.
解:(1)依题意,因为lx( )ÎL ,
0(), fx x Î R
所以"Î-+xxxkRx, + 2 1,且 x R,-+=xx2kx + 1,····················1分
„ 0 00 0
令f()x(x1k=)-+x- 12 - ,D=- ( k- 1 )2 4,
则f()x 0 ,且f(x )=0,
„ 0
ì D 0,
所以í „ 所以D= 0, ···································································3分
î D 0,
…
即 ( k-- 1=) 42 0 ,
解得k =3或- 1. ··············································································4分
(2)(ⅰ)先证必要性.
( )
若直线yl=x ( ) 是曲线yg= x ( ) 的切线,设切点为 x ,ex0 +1 ,
0
( )
因为g¢()x =e x,所以切线方程为yx-+=ex1x0e( - )x0 ,
0
即lx ( x )=+e-(x01x)e +1 x0 (*).························································5分
0
一方面,gx ( l x )= ( ) ,所以$Î xgxlRx,(=)( ) ,································6分
0 0 00 0
参考答案 第 7 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}另一方面,令Gx ( gx ) l=xx-=-- ( - ) x ( ) eex(1)ex0 x0,则G ( x )=0,
0 0
因为G ¢ ( x )=ex - ex0,
所以当x< x 时,G ¢ ( x )<0,G ( x ) 在 (¥- ,x ) 单调递减,
0 0
当x>x 时,G ¢ ( x )>0,G ( x ) 在 ( x ,+¥ ) 单调递增,
0 0
所以Gx
(
G
)
x
( )=0,所以gx (
l
)
x
( )
.··············································7分
… 0 …
即" ÎxgxlRx,()( ) ,
…
所以lx
( )ÎT
,即l(x)是函数g(x)在R上的“最佳下界线”.···············8分
gx(),x Î R
再证充分性.
若l(x)是函数g(x)在R上的“最佳下界线”,不妨设lx(kx)=b + ,
由“最佳下界线”的定义," ÎxgxlR,x ( ) ( ) ,且$Î xgxlRx, =( ) ( ) ,····9分
… 00 0
令Hx
(
gx
) lx=k-=x+(-
b
)- ( )
ex 1 ,
则H ( x ) 0且H ( x )=0,所以H ( x ) =0. ·········································10分
… 0 min
因为Hx ¢ ( )=exk- ,
①若k 0,则H ¢ ( x ) 0,所以H ( x ) 在R上单调递增,
„ …
所以$ x< x ,使得Hx ( H ) x< ( )=0,故k 0不符合题意.·····················11分
1 0 1 0 „
②若k >0,令H ¢ ( x )=0,得x=lnk,
当x¥Î- ( ,lnk ) 时,H ¢ ( x )<0,得H ( x ) 在 (¥- ,lnk ) 单调递减,
当xÎ+¥( lnk, ) 时,H ( x )>0,得H ( x ) 在 ( lnk,+¥ ) 单调递增,
所以,当且仅当x=lnk时,H ( x ) 取得最小值H ( lnk ) .····························12分
又由H ( x ) 在x 处取得最小值,H ( x ) =0,
0 min
ì x =lnk,
所以í 0 ···········································································13分
î H(ln)k0,=
即 ï í ì k =ex0, 解得k =ex 0 ,b=-( 1e x )+1x0 ,····························14分
ïî e1x 00+,-- =kx b 0
0
所以lx ( x )=+e-(x01x)e +1 x0 ,
0
参考答案 第 8 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}( )
由(*)式知直线yl=x( )是曲线yg=x( )在点 x ,ex0 +1 处的切线. ············15分
0
综上所述,直线yl=x( )是曲线yg=x( )的一条切线的充要条件是直线yl=x( )是函数
g(x)在R上的“最佳下界线”.
(ⅱ)集合L T 元素个数为2个. ············································17分
hx()x,g(1x,)Î+(x¥), I Î R
参考答案 第 9 页 共9页
{{##{{QQQQAABBJIYYAC8U5oggCigwQwIIBTAAACRJ5hqCRQUQGG0gCCgggEQQskIABhELAKAoCEoRGRhCAHAqIIAARALBiJyNAINBAIAB=A}A#}=}#}