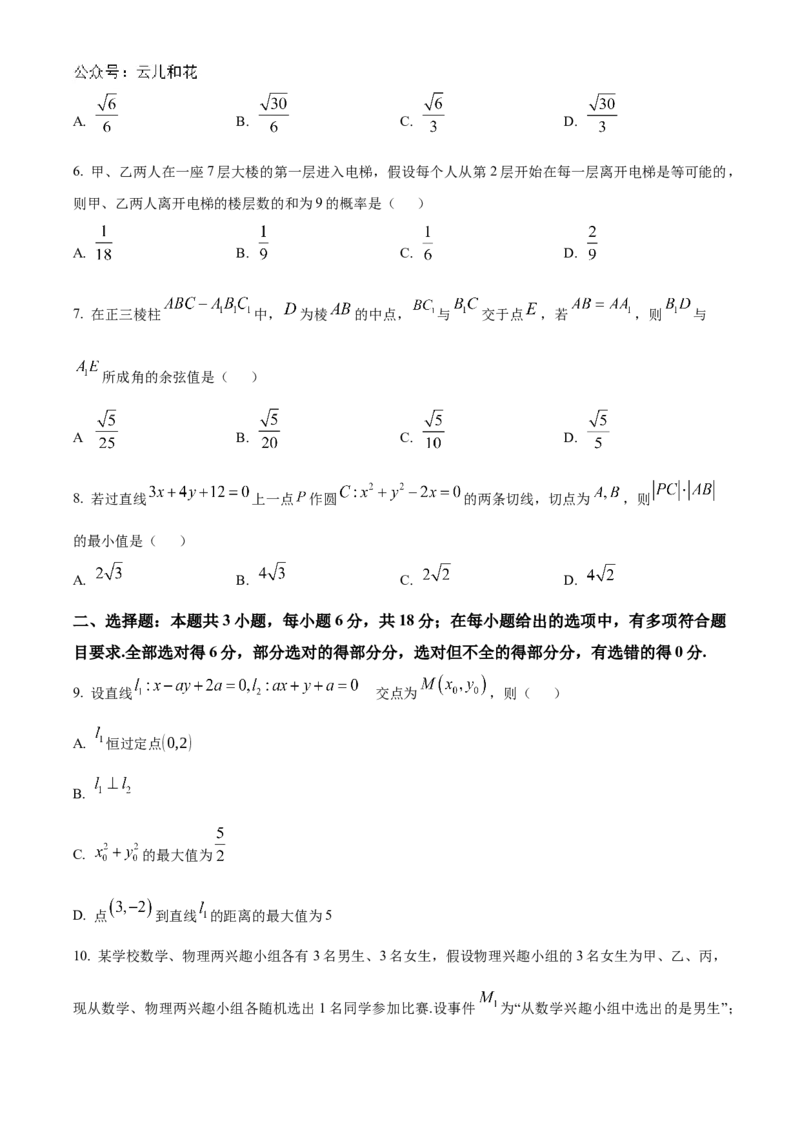文档内容
2024~2025 学年度第一学期期中教学质量检测
高二数学试题
注意事项:
1.答卷前,考生务必将自己的考场、座号、姓名、班级填(涂)写在答题卡上,将条形码粘
贴在”贴条形码区”.
2.作选择题时,选出每小题答案后,用 2B铅笔把答题卡上对应题目选项的答案信息点涂黑;
如需改动,用橡皮擦干净后,再改涂其它答案标号.
3.非选择题须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡中各题目指定的区域内相
应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.否
则,该答题无效.
4.考生必须保持答题卡的整洁;书写力求字体工整、符号规范、笔迹清楚.
一、选择题:本题共8小题,每小题5分,共40分;在每小题给出的四个选项中,只有一个
选项是正确的.
1. 已知空间两点 ,则 两点间的距离是( )
A. 2 B. 3 C. 4 D. 9
2. 若直线 经过点 ,则直线 的斜率是( )
A. B. C. D.
3. 甲、乙两人比赛下棋,下成和棋的概率是 ,甲获胜的概率的是 ,则乙不输的概率是( )
A. B. C. D.
4. 已知直线 与圆 相交于 两点,则 ( )
A. B. 4 C. D. 2
的
5. 已知空间三点 ,则点 到直线 距离是( )A. B. C. D.
6. 甲、乙两人在一座7层大楼的第一层进入电梯,假设每个人从第2层开始在每一层离开电梯是等可能的,
则甲、乙两人离开电梯的楼层数的和为9的概率是( )
A. B. C. D.
7. 在正三棱柱 中, 为棱 的中点, 与 交于点 ,若 ,则 与
所成角的余弦值是( )
.
A B. C. D.
8. 若过直线 上一点 作圆 的两条切线,切点为 ,则
的最小值是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分;在每小题给出的选项中,有多项符合题
目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.
9. 设直线 交的点为 ,则( )
A. 恒过定点(0,2)
B.
C. 的最大值为
D. 点 到直线 的距离的最大值为5
10. 某学校数学、物理两兴趣小组各有3名男生、3名女生,假设物理兴趣小组的3名女生为甲、乙、丙,
现从数学、物理两兴趣小组各随机选出1名同学参加比赛.设事件 为“从数学兴趣小组中选出的是男生”;事件 为“从物理兴趣小组选出的是女生乙”;事件 为“从两兴趣小组选出的都是男生”;事件 为
“从两兴趣小组中选出的是1名男生和1名女生”,则( )
A. B.
C. 与 相互独立 D. 与 互斥
11. 已知正方体 的棱长为2,点 满足 ,其中 ,
则( )
A. 存在唯一点 ,使得 平面
B. 存在唯一点 ,使得 平面
C. 当 时,点 到平面 的距离的最小值为
D. 当 时,三棱锥 的体积的最小值为
三、填空题:本题共3个小题,每小题5分,共15分.
12. 若实数 满足方程 ,则 的最小值为___.
13. 某商场调查500名顾客的满意度情况,得到的数据如下表:
不满意 一般 满意
女性 25 64
男性 15 36
若 ,则满意的顾客中男性顾客不少于女性顾客的概率为________.
14. 已知正四棱柱 为对角线 的中点,过点 的直线与长方体表
面交于 两点, 为长方体表面上的动点,则 的取值范围是__________.
四、解答题:本题共5小题,共77分;解答应写出文字说明、证明过程或演算步骤.15. 如图,长方体 中, ,设 .
(1)证明: 平面 ;
(2)求平面 与平面 夹角的余弦值.
16. 在某电视民间歌手挑战赛活动中,有4位民间歌手参加比赛,由现场观众投票选出最受欢迎的歌手,
各位观众须彼此独立地在选票上选2名歌手.其中观众甲是1号歌手的歌迷,他必选1号,另外在其他歌手
中随机选1名;观众乙、丙对4位歌手没有偏爱,因此,乙、丙在4名歌手中随机选2名歌手.
(1)求观众甲选2号歌手且观众乙未选2号歌手的概率;
(2)设3号歌手得到观众甲、乙、丙的选票数之和为 ,求 的概率.
17. 已知直线 经过直线 的交点 ,且A(3,2)、 两点到直线
的距离相等.
(1)求直线 的一般式方程;
(2)若点 在直线 的同侧,且 为直线 上一个动点,求 的最小值.
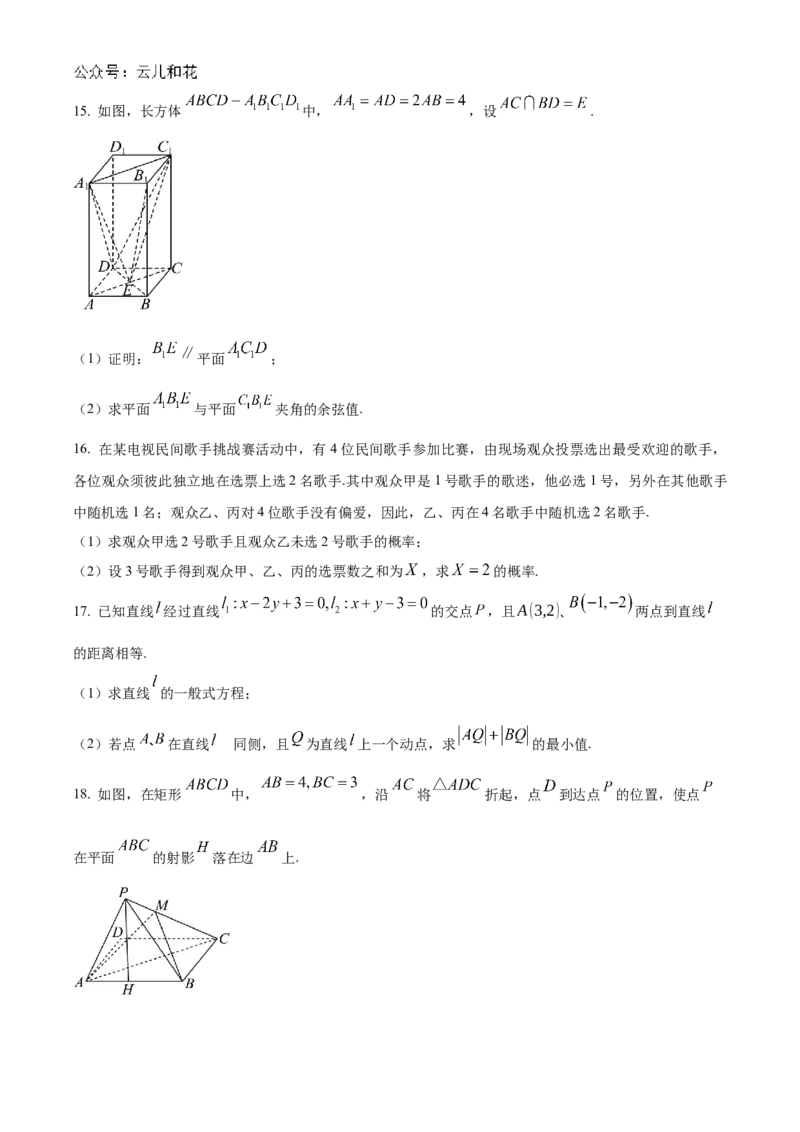
18. 如图,在矩形 中, ,沿 将 折起,点 到达点 的位置,使点
在平面 的射影 落在边 上.(1)证明: ;
(2)求点 到平面 的距离;
的
(3)若 ,求直线 与平面 所成角 正弦值.
19. 在平面直角坐标系中,已知圆 经过原点和点 ,并且圆心在 轴上.
(1)求圆 的标准方程;
(2)设 为圆 的动弦,且 不经过点 ,记 分别为弦 的斜率.
(i)若 ,求 面积的最大值;
(ii)若 ,请判断动弦 是否过定点?若过定点,求该定点坐标;若不过定点,请说明理由.