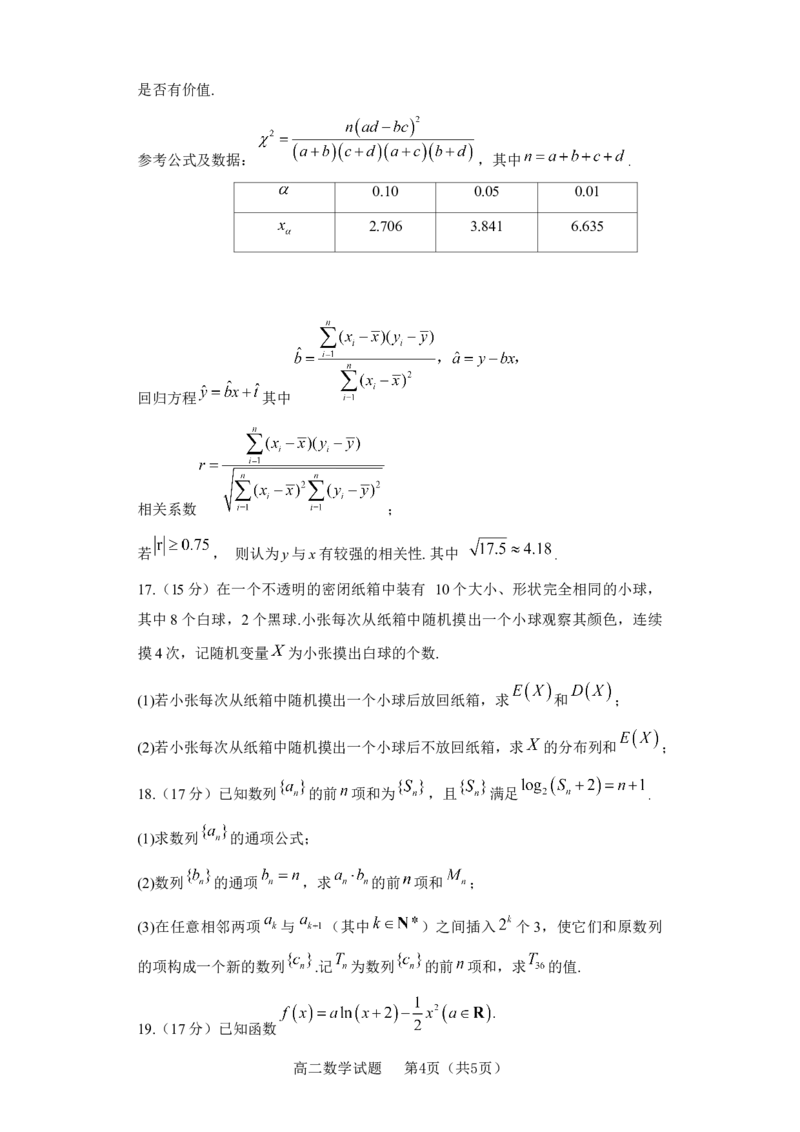文档内容
参照秘密级管理★启用前
2023—2024 学年度第二学期高二教学质量检测
数 学
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答
案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.设等差数列 ,则
A. -5 B. 18 C. 23 D. 28
2. 若函数 满足 则
A. B. C. D.
3. 设 是等比数列,且 ,则公比
A. -2 B. 2 C. -8 D. 8
4. 在 的展开式中,含 的项的系数为
A. -280 B. 280 C. -560 D.
560
5.某志愿者小组有5人,从中选3人到A、B两个社区开展活动,其中1人到A社
区,则不同的选法有
A. 12种 B. 24种 C. 30
种 D. 60种
6. 直线 与曲线 相切, 则实数k的值为
A. 1 B. C. D.
7. 若 则
A. B. C.
高二数学试题 第1页(共5页)D.
8. 不等式 的解集是
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的四个选项中,
有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0
分.
9.已知随机变量 ,则下列说法正确的是
A. 若 , 则 B. 若 ,则
C. D.
10. 若函数 的定义域为 , 其导函数
的图象如图所示,则
A. 有两个极大值点 B. 有一个极小值
点
C. D.
11.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中提出了一些新的垛
积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,
但是逐项差数之差或者高次差成等差数列. 如数列 ,它的前后两项之差
组成新数列 ,新数列 为等差数列, 则数 被称为二阶等差数
列,现有二阶等差数列 ,其前6项分别为 ,设其通项公式
则下列结论中正确的是
A. 数列 的公差为 2 B.
C. 数列 的前7项和最大 D.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知 ,
则 ________.
13. 已知随机变量X 的分布列如下:
高二数学试题 第2页(共5页)0 1 2
0.6
若 , 则 .
14. 人们为了解一支股票未来一定时期内价格的变化,往往会去分析影响股票价格
的基本因素,比如利率的变化.现假设人们经分析估计利率下调的概率为 60%,利
率不变的概率为40%.根据经验,人们估计,在利率下调的情况下,该支股票价格
上涨的概率为80%,而在利率不变的情况下,其价格上涨的概率为40%,则该支
股票将上涨的概率为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步
骤.
15.(13分)已知函数 .
(1)求 的值, 并写出 的表达式;
(2)证明: .
16.(15分)近年来,养宠物的人越来越多,在供需端及资本的共同推动下中国宠
物经济产业迅速增长,数据显示,目前中国养宠户数在全国户数中占比为 .
(1)随机抽取200名成年人,并调查这200名成年人养宠物的情况,统计后得到如
下列联表:
成年男性 成年女性 合计
养宠物 38 60 98
不养宠物 62 40 102
合计 100 100 200
依据小概率值 的独立性检验,判断能否认为养宠物与性别有关?
(2)记2018-2023年的年份代码x依次为 中国宠物经济产业年规模为y
(单位:亿元),由这6年中国宠物经济产业年规模数据求得y,关于x的回归方
程为 ,且 . 求相关系数r并判断该回归方程
高二数学试题 第3页(共5页)是否有价值.
参考公式及数据: ,其中 .
0.10 0.05 0.01
2.706 3.841 6.635
回归方程 其中
相关系数 ;
若 , 则认为y与x有较强的相关性. 其中 .
17.(15分)在一个不透明的密闭纸箱中装有 10个大小、形状完全相同的小球,
其中8个白球,2个黑球.小张每次从纸箱中随机摸出一个小球观察其颜色,连续
摸4次,记随机变量 为小张摸出白球的个数.
(1)若小张每次从纸箱中随机摸出一个小球后放回纸箱,求 和 ;
(2)若小张每次从纸箱中随机摸出一个小球后不放回纸箱,求 的分布列和 ;
18.(17分)已知数列 的前 项和为 ,且 满足 .
(1)求数列 的通项公式;
(2)数列 的通项 ,求 的前 项和 ;
(3)在任意相邻两项 与 (其中 )之间插入 个3,使它们和原数列
的项构成一个新的数列 .记 为数列 的前 项和,求 的值.
19.(17分)已知函数
高二数学试题 第4页(共5页)(1)讨论函数 的单调性;
(2)若函数 有两个极值点,
(i)求实数a的取值范围;
(ii)证明:函数 有且只有一个零点.
高二数学试题 第5页(共5页)