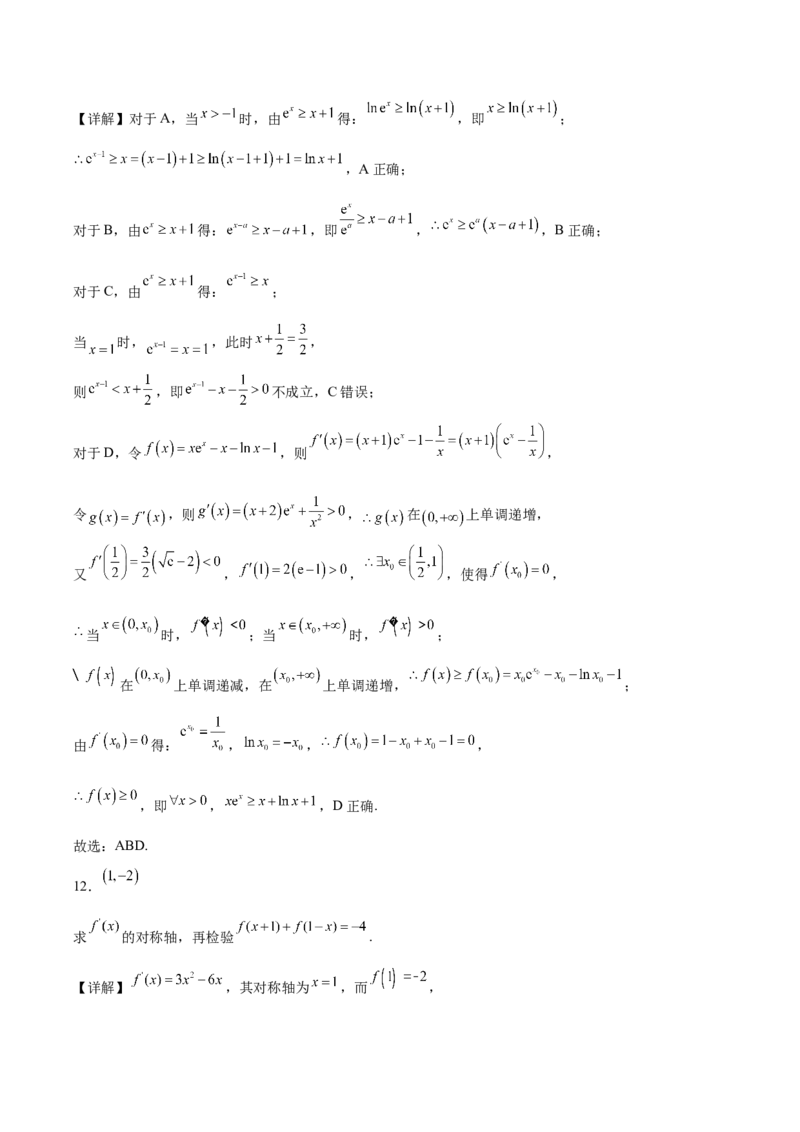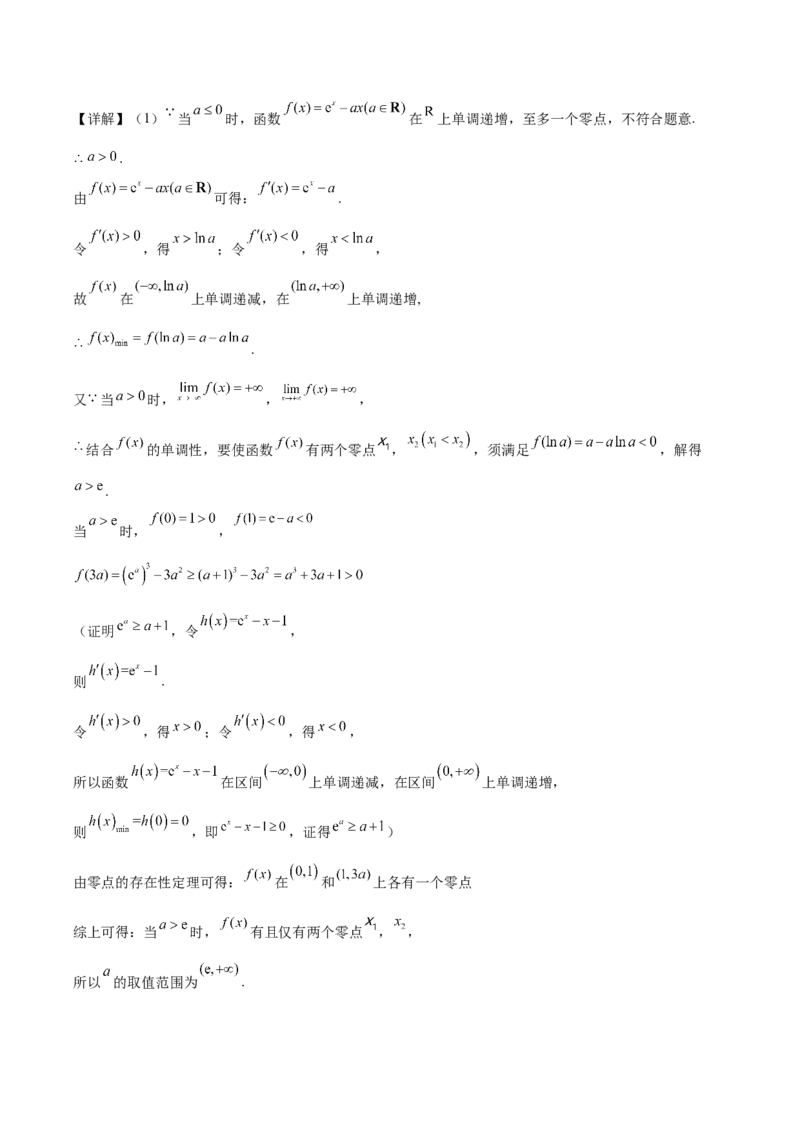文档内容
山东省滕州市第一中学2024-2025学年
高二下学期3月单元过关考试数学
一、单选题
1.下列各式正确的是( )
A. ( 为常数) B.
C. D.
2.一质点做直线运动,其位移 与时间 的关系为 ,设其在 内的平均速度为 ,在
时的瞬时速度为 ,则 ( )
A. B. C. D.
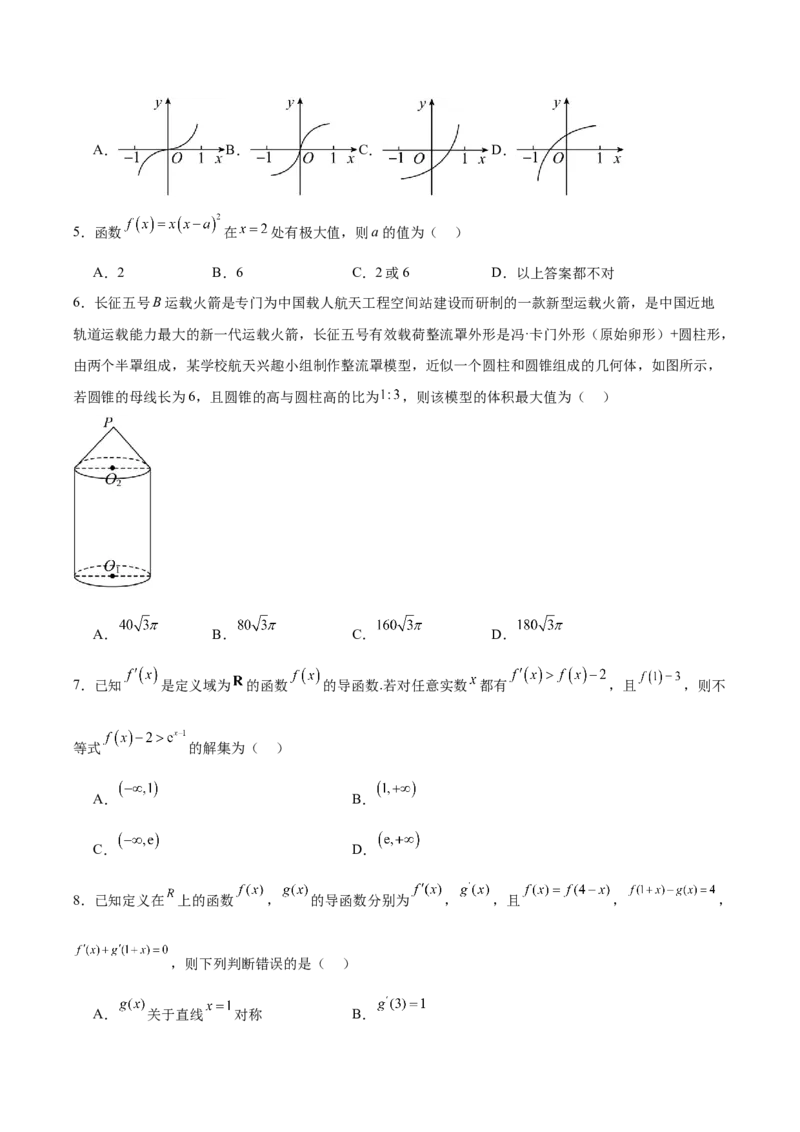
3.如图,一圆形信号灯分成 四块灯带区域,现有3种不同的颜色供灯带使用,要求在每块灯带
里选择1种颜色,且相邻的2块灯带选择不同的颜色,则不同的信号总数为( )
A.18 B.24 C.30 D.42
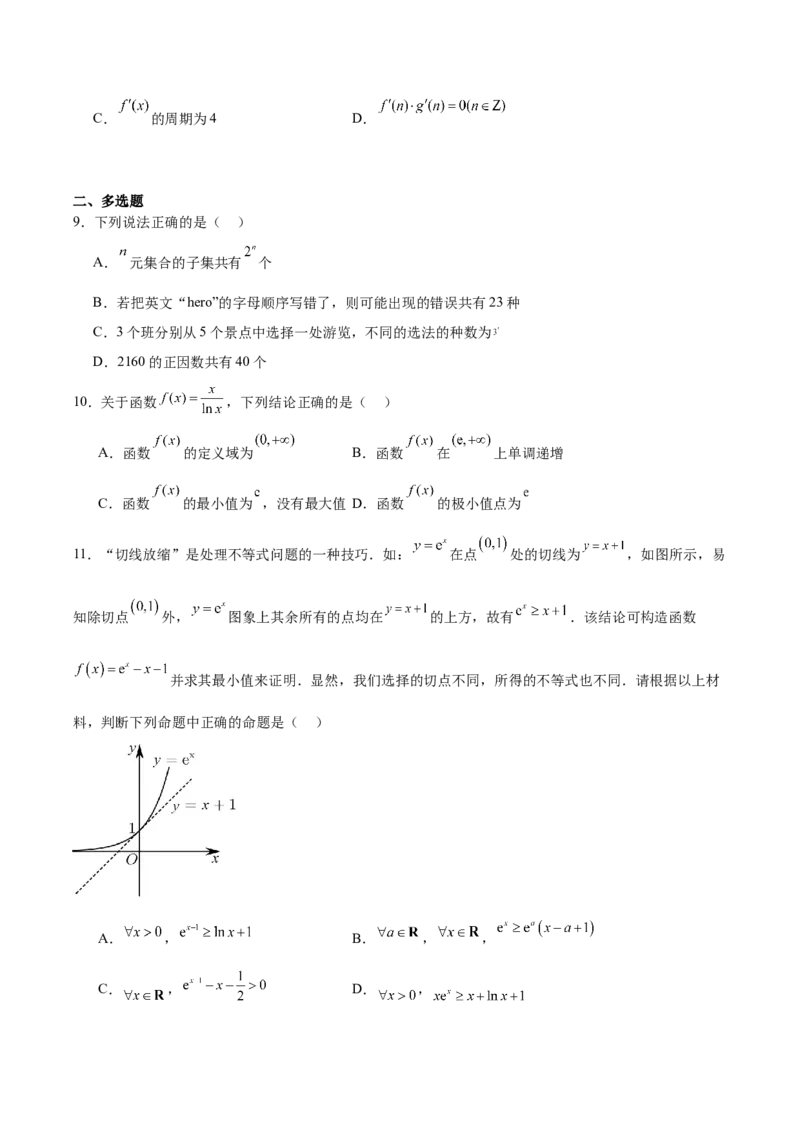
4.已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图
象是( )A. B. C. D.
5.函数 在 处有极大值,则a的值为( )
A.2 B.6 C.2或6 D.以上答案都不对
6.长征五号B运载火箭是专门为中国载人航天工程空间站建设而研制的一款新型运载火箭,是中国近地
轨道运载能力最大的新一代运载火箭,长征五号有效载荷整流罩外形是冯·卡门外形(原始卵形)+圆柱形,
由两个半罩组成,某学校航天兴趣小组制作整流罩模型,近似一个圆柱和圆锥组成的几何体,如图所示,
若圆锥的母线长为6,且圆锥的高与圆柱高的比为 ,则该模型的体积最大值为( )
A. B. C. D.
7.已知 是定义域为 的函数 的导函数.若对任意实数 都有 ,且 ,则不
等式 的解集为( )
A. B.
C. D.
8.已知定义在 上的函数 , 的导函数分别为 , ,且 , ,
,则下列判断错误的是( )
A. 关于直线 对称 B.C. 的周期为4 D.
二、多选题
9.下列说法正确的是( )
A. 元集合的子集共有 个
B.若把英文“hero”的字母顺序写错了,则可能出现的错误共有23种
C.3个班分别从5个景点中选择一处游览,不同的选法的种数为
D.2160的正因数共有40个
10.关于函数 ,下列结论正确的是( )
A.函数 的定义域为 B.函数 在 上单调递增
C.函数 的最小值为 ,没有最大值 D.函数 的极小值点为
11.“切线放缩”是处理不等式问题的一种技巧.如: 在点 处的切线为 ,如图所示,易
知除切点 外, 图象上其余所有的点均在 的上方,故有 .该结论可构造函数
并求其最小值来证明.显然,我们选择的切点不同,所得的不等式也不同.请根据以上材
料,判断下列命题中正确的命题是( )
A. , B. , ,
C. , D. ,三、填空题
12.函数 图像的对称中心为 .
13.已知函数 在 上不单调,则实数 的取值范围为 .
14.【2016高考新课标2改编】如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处
的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为 .
四、解答题
15.已知函数 , .
(1)求曲线 在 处切线的方程;
(2)若直线l过坐标原点且与曲线 相切,求直线l的方程.
16.已知函数 .
(1)若 ,求函数 的单调区间;
(2)若函数 在 上是减函数,求实数 的取值范围.
17.已知函数 在 处有极值.
(1)求函数 在区间 上的最大值和最小值;
(2)若方程 有且只有一个实数根,求实数 的取值范围.
18.已知函数 .(1)若函数 有两个零点 , ,求 的取值范围;
(2)在(1)的条件下,求证: .
19.已知函数
(1)讨论 的单调性;
(2)若 有两个零点,求 的取值范围.题号 1 2 3 4 5 6 7 8 9 10
答案 C B A B B C B B ABD BD
题号 11
答案 ABD
1.C
利用导数的运算法则来进行求导即可作出判断.
【详解】因为当 为常数时, ,所以A错误;
因为 ,所以B错误;
因为 ,所以C正确;
因为 ,所以D错误;
故选:C.
2.B
根据平均变化率和瞬时变化率的定义,可分别计算求得 , 即可得出结果.
【详解】根据平均速度定义可知,
在 内的平均速度为 ;
在 时的瞬时速度为 ;
所以 .
故选:B
3.A
根据涂色问题,按照使用颜色种数进行分类,再结合分步计数原理,即可得总的方法数.
【详解】若用3种不同的颜色灯带,故有两块区域涂色相同,要么 ,要么 相同,有2种方案,则
不同的信号数为 ;若只用2种不同的颜色灯带,则 颜色相同, 颜色相同,只有1种方案,则不同的信号数为
;
则不同的信号总数为 .
故选:A.
4.B
【详解】由y=f′(x)的图象知,y=f(x)的图象为增函数,
且在区间(-1,0)上增长速度越来越快,
而在区间(0,1)上增长速度越来越慢.
故选B.
5.B
由函数 在 处有极大值,求得 或 ,再分类讨论,结函数极值的概念进行判定,
即可求解.
【详解】由题意,函数 ,则 ,
因为函数 在 处有极大值,
则 ,即 ,解得 或 ,
(1)当 时,可得 ,令 ,解得 或 ,
当 时, ,函数 单调递增,
当 时, ,函数 单调递减,
时, ,函数 单调递增,
所以当 时,函数 取得极小值,不符合题意(舍去);
(2)当 时,可得 ,令 ,解得 或 ,
当 时, ,函数 单调递增,当 时, ,函数 单调递减,
时, ,函数 单调递增,
所以当 时,函数 取得极大值,符合题意,
综上可得,当 时,函数 在 处有极大值.
故选:B.
6.C
设出圆锥的高,由圆锥与圆柱的体积公式列式,由导数判断单调性后求解最值,
【详解】设圆锥的高为 ,则圆柱的高为 ,底面圆半径为 ,
则该模型的体积 ,
令 ,则 ,由 得 ,
当 时 ,当 时 ,
则 在 上单调递增,在 上单调递减,
当 时, ,
故选:C
7.B
依题意原等价于不等式 ,构造函数 ,利用导数说明函数的单调性,即可得到
,从而得解;
【详解】解:不等式 ,等价于不等式 ,
构造函数 ,则 ,
若对任意实数 都有 ,
则 , 在 上单调递增,又 ,
故 即 ,
故不等式的解集是 ,
故选:B.
8.B
由题意,根据函数的对称性,合理赋值即可判断A;利用导数求导可得 、 ,
通过合理赋值即可判断BCD.
【详解】由 ,得 ①,
②,得 ③,
由①②③,得 ,所以函数 图象关于直线 对称,故A正确;
由 ,得 ,令 ,得 ;
由 ,得 ,
令 ,得 ,
∴ ④,
又 ⑤,令 ,得 ,故B错误;
④⑤两式相加,得 ,得 ,
所以 ,即函数 的周期为4,故C正确;
由 ,令 ,得 ,所以 ,
所以 ,故D正确.
故选:B
9.ABD
A. 元集合的子集共有 个判断;B.把h,e,r,o全排列有 判断;C.由每个班有5种选法判断.D.
由 判断.【详解】A. 元集合的子集共有 个,故正确;
B.把h,e,r,o全排列有 ,其中正确的有一个,所以可能出现的错误共有23种,故正确;
C. 3个班分别从5个景点中选择一处游览,不同的选法的种数为 ,故错误;
D. 因为 ,所以2160的正因数共有 个,故正确;
故选:ABD
10.BD
对于A,注意到 可知 ,由此可判断;
对于B,对 求导,利用导数与函数的单调性的关系可判断其正确;
对于C,举反例排除即可;
对于D,利用导数与函数极值的关系可判断其正确.
【详解】对于A,因为 ,所以 ,解得 ,故 的定义域为 ,故A
错误;
对于B, ,令 ,得 ,故 在 上单调递增,故B正确;
对于C,令 ,则 ,故 的最小值不为 ,故C错误;
对于D,令 ,得 或 ,所以 在 和 上单调递减,
令 ,得 ,故结合 两侧的单调性可知 是 的极小值点,故D正确.
故选:BD.
11.ABD
利用 可得 ,由 知A正确;由 知B正确;利用反
例可说明C错误;令 ,利用导数可求得 ,知D正确.【详解】对于A,当 时,由 得: ,即 ;
,A正确;
对于B,由 得: ,即 , ,B正确;
对于C,由 得: ;
当 时, ,此时 ,
则 ,即 不成立,C错误;
对于D,令 ,则 ,
令 ,则 , 在 上单调递增,
又 , , ,使得 ,
当 时, ;当 时, ;
在 上单调递减,在 上单调递增, ;
由 得: , , ,
,即 , ,D正确.
故选:ABD.
12.
求 的对称轴,再检验 .
【详解】 ,其对称轴为 ,而 ,,
故 图像的对称中心为
故答案为:
13.
【详解】函数 在 上不单调,
即 在 有零点,
即
当 , ,故
故答案为:
14.18
【详解】由题意,要使小明从街道的 处出发到 处最短,小明需走两纵两横四段路,共有 条不同的路,
再从 处到 处最短共有 条路,则小明到老年公寓可以选择的最短路径条数为 ,故答案为
.
15.(1)
(2)
【详解】(1) ,所以 ,所以 , ,所
以切线方程为: ,整理得 .(2) ,所以 ,设切点坐标为 ,所以切线斜率为 ,
则切线方程为: ,又因为切线过原点,所以将 代入切线方程得 ,
解得 ,所以切线方程为: ,整理得 .
16.(1)单调递减区间是 ,单调递增区间是 ,
(2)
【详解】(1)当 时, ,
,
所以 的单调递减区间是 ,单调递增区间是
(2)由函数 在 上是减函数,知 恒成立,
.
由 恒成立可知 恒成立,则 ,
设 ,则 ,
由 , 知,
函数 在 上递增,在 上递减,
∴ ,∴ .
17.(1) ,(2)
【详解】(1)因为 ,该函数的定义域为 ,且
由已知可得 ,解得 .
所以 , ,
由 ,可得 或 ,
由 ,可得 ,
所以 在 单调递增,在 单调递减,
当 时,函数 在 上单调递减,在 上单调递增,
因为 , ,则 ,
.
(2)解:
在 上单调递增,在 上单调递减,在 上单调递增
所以 的极大值为 , 的极小值为
且 , , ,
若方程 有且只有一个实数根,.
则 需满足 ,或 .
所以实数 的取值范围
18.(1)
(2)证明见解析【详解】(1) 当 时,函数 在 上单调递增,至多一个零点,不符合题意.
.
由 可得: .
令 ,得 ;令 ,得 ,
故 在 上单调递减,在 上单调递增,
.
又 当 时, , ,
结合 的单调性,要使函数 有两个零点 , ,须满足 ,解得
.
当 时, ,
(证明 ,令 ,
则 .
令 ,得 ;令 ,得 ,
所以函数 在区间 上单调递减,在区间 上单调递增,
则 ,即 ,证得 )
由零点的存在性定理可得: 在 和 上各有一个零点
综上可得:当 时, 有且仅有两个零点 , ,
所以 的取值范围为 .(2)证明:由(1)可知 , 是函数 的两个零点,
所以 , ,解得 , ,
则 .
设 ,
则 ,解得 , .
要证 ,
只要证 ,
即证 .
令 ,
则 ,
所以函数 在 上单调递增,
所以 ,
即证得 .
19.(1)见解析;(2) .
解析:(1) 的定义域为 , ,(ⅰ)若 ,
则 ,所以 在 单调递减.
(ⅱ)若 ,则由 得 .当 时, ;当 时, ,所以 在 单调递减,在
单调递增.
(2)(ⅰ)若 ,由(1)知, 至多有一个零点.
(ⅱ)若 ,由(1)知,当 时, 取得最小值,最小值为 .
①当 时,由于 ,故 只有一个零点;
②当 时,由于 ,即 ,故 没有零点;
③当 时, ,即 .
又 ,故 在 有一个零点.
设正整数 满足 ,则 .
由于 ,因此 在 有一个零点.