文档内容
2024-2025 学年山东省滨州市高二上学期 1 月期末数学试题❖
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.椭圆 的焦点坐标为
A. 和 B. 和
C. 和 D. 和
2.过点 且与直线 平行的直线的方程为( )
A. B. C. D.
3.已知点G为平行四边形ABCD对角线的交点,点P为空间任意一点,则
A. B. C. D.
4.已知 是函数 的导函数,且 ,则
A. 1 B. 2 C. D.
5.与圆 及圆 都内切的圆的圆心在
A. 椭圆上 B. 双曲线的左支上 C. 双曲线的右支上 D. 抛物线上
6.按照《全国人民代表大会常务委员会关于实施渐进式延迟法定退休年龄的决定》,我国自2025年1月1
日起,逐步将男职工的法定退休年龄从原60周岁延迟到63周岁.对于男职工,新方案按照出生时间延迟法
定退休年龄,每4个月延迟1个月,当不满4个月时仍按延迟1个月计算.男职工延迟法定退休年龄部分对
照表如下:
1965年 1965年 1965年 1966年
出生时间
1月至4月 5月至8月 9月至12月 1月至4月
改革后法定
60岁1个月 60岁2个月 60岁3个月 60岁4个月
退休年龄
那么1973年5月出生的男职工退休年龄为A. 61岁3个月 B. 62岁 C. 62岁1个月 D. 62岁2个月
7.在直四棱柱 中,底面ABCD是正方形, , ,点N在棱 上,若直线
到平面ABN的距离为 ,则 的值为
A. 1 B. C. D.
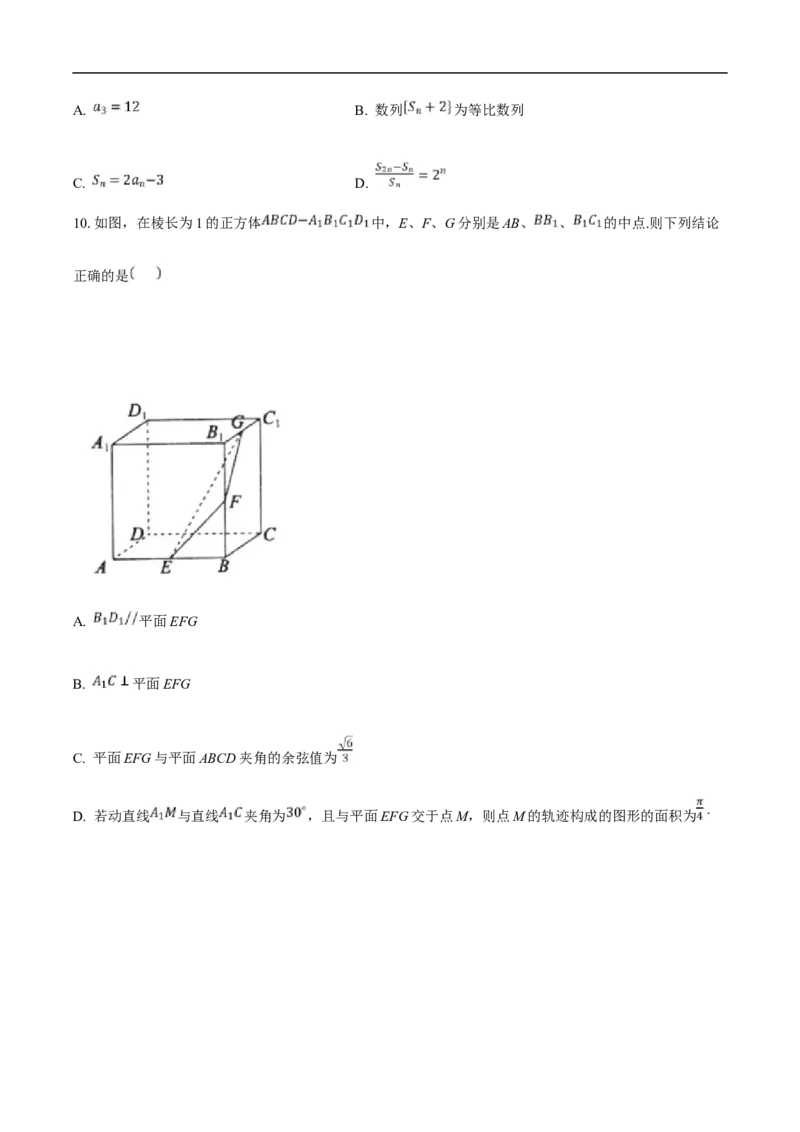
8.如图所示,用一个与圆柱底面成 角的平面截圆柱,截口曲线是一个椭圆, , 为该椭圆
的焦点,P为椭圆上任意一点.若圆柱的底面圆半径为1, ,则下列结论不正确的是
A. 椭圆的长轴长为4 B. 椭圆的离心率为
C. 满足 的点P共有4个 D. 的最大值为8
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,
部分选对的得2分,有选错的得0分。
9.已知等比数列 的前n项和为 ,且 , ,则下列结论正确的是A. B. 数列 为等比数列
C. D.
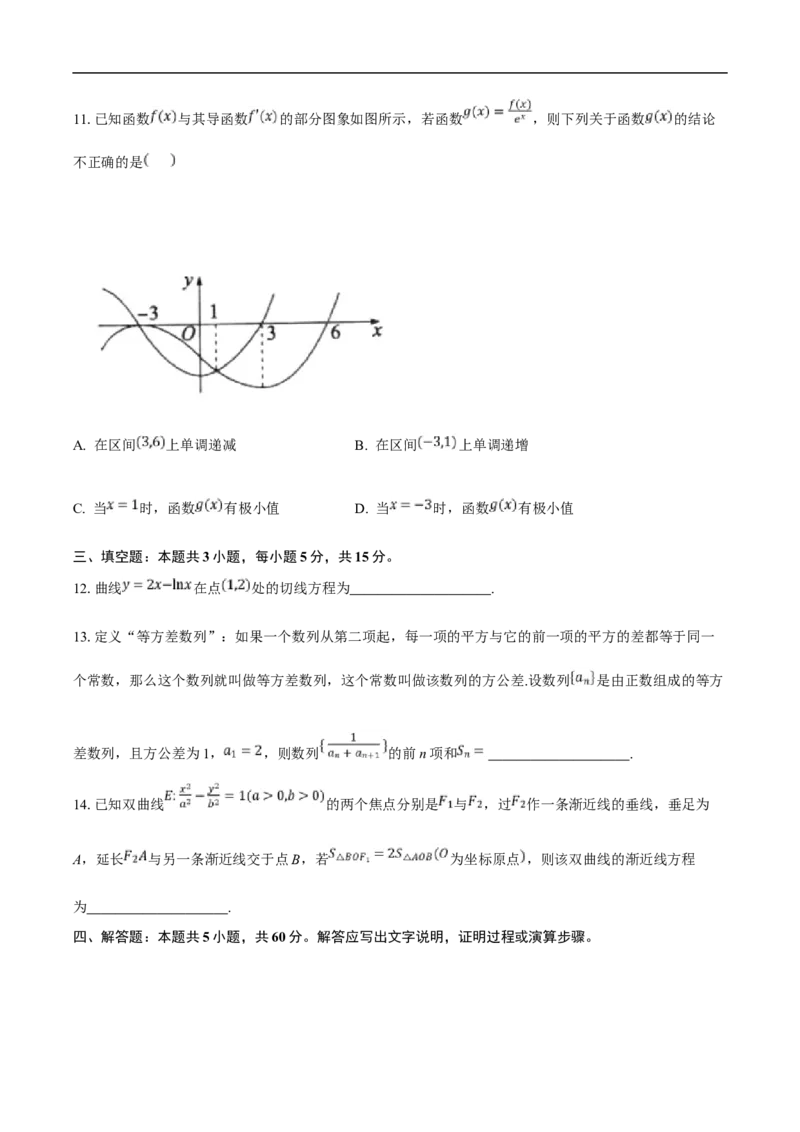
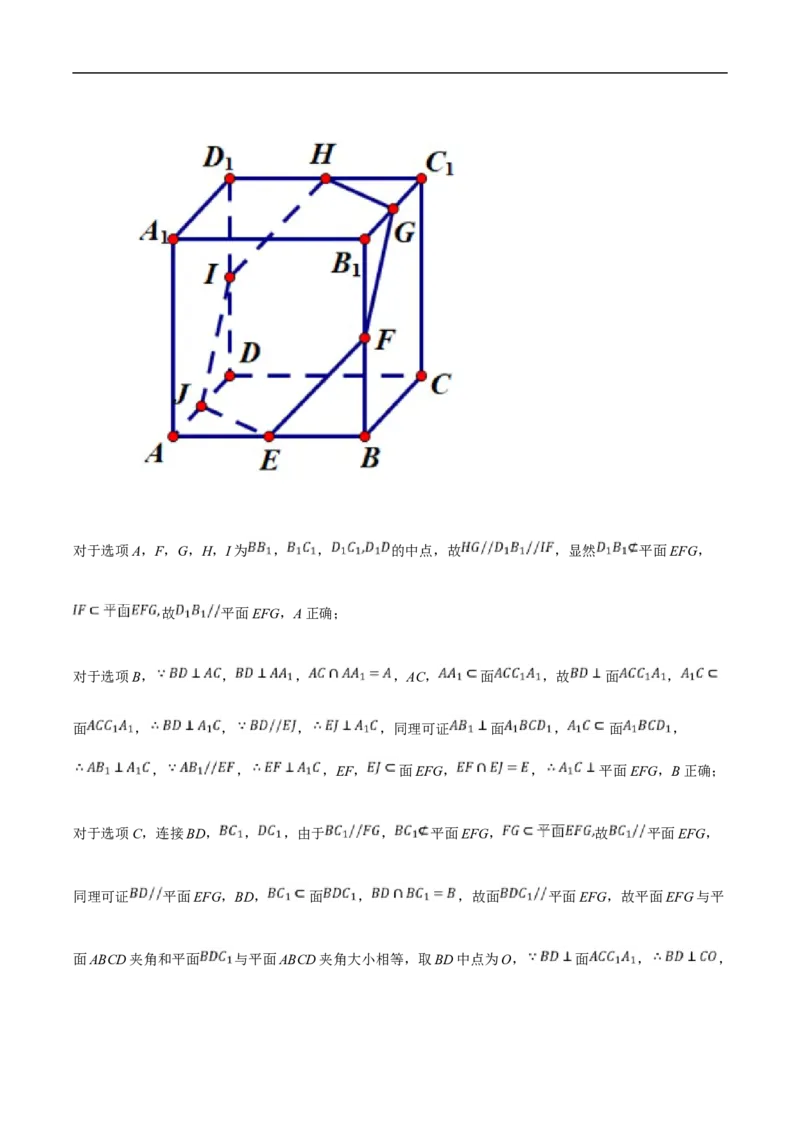
10.如图,在棱长为1的正方体 中,E、F、G分别是AB、 、 的中点.则下列结论
正确的是
A. 平面EFG
B. 平面EFG
C. 平面EFG与平面ABCD夹角的余弦值为
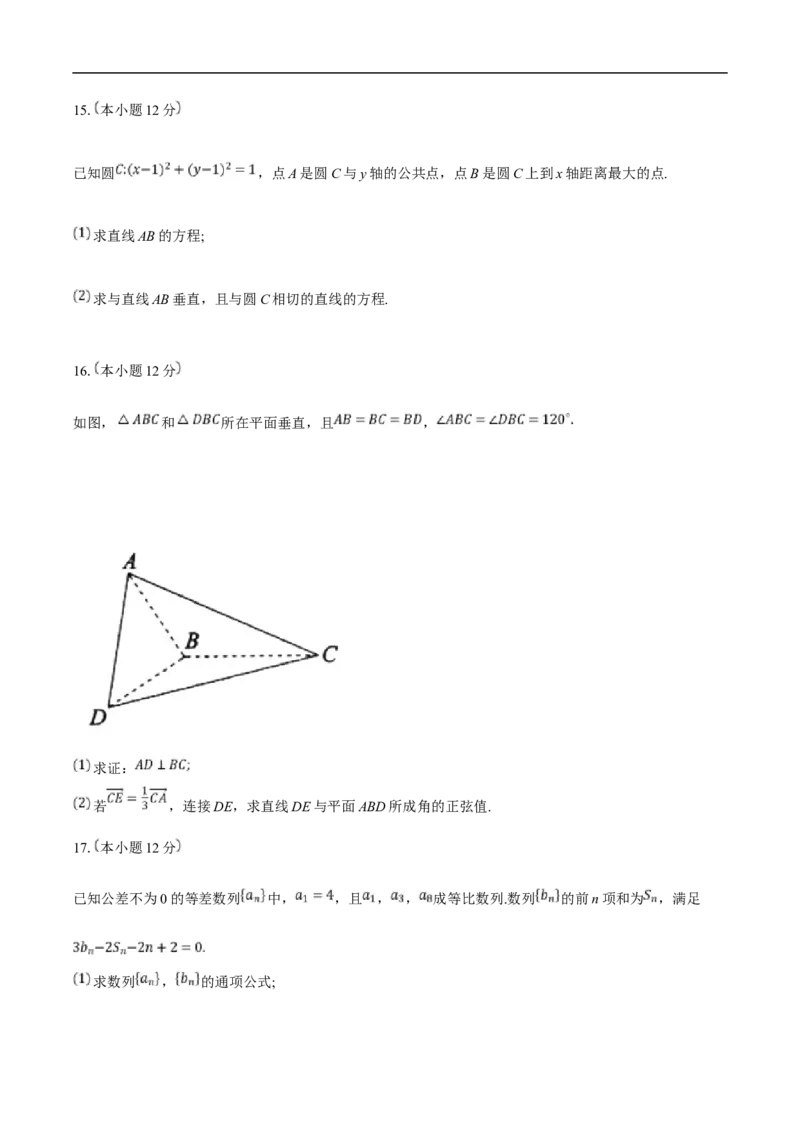
D. 若动直线 与直线 夹角为 ,且与平面EFG交于点M,则点M的轨迹构成的图形的面积为11.已知函数 与其导函数 的部分图象如图所示,若函数 ,则下列关于函数 的结论
不正确的是
A. 在区间 上单调递减 B. 在区间 上单调递增
C. 当 时,函数 有极小值 D. 当 时,函数 有极小值
三、填空题:本题共3小题,每小题5分,共15分。
12.曲线 在点 处的切线方程为 .
13.定义“等方差数列”:如果一个数列从第二项起,每一项的平方与它的前一项的平方的差都等于同一
个常数,那么这个数列就叫做等方差数列,这个常数叫做该数列的方公差.设数列 是由正数组成的等方
差数列,且方公差为1, ,则数列 的前n项和 .
14.已知双曲线 的两个焦点分别是 与 ,过 作一条渐近线的垂线,垂足为
A,延长 与另一条渐近线交于点B,若 为坐标原点 ,则该双曲线的渐近线方程
为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。15. 本小题12分
已知圆 ,点A是圆C与y轴的公共点,点B是圆C上到x轴距离最大的点.
求直线AB的方程;
求与直线AB垂直,且与圆C相切的直线的方程.
16. 本小题12分
如图, 和 所在平面垂直,且 ,
求证:
若 ,连接DE,求直线DE与平面ABD所成角的正弦值.
17. 本小题12分
已知公差不为0的等差数列 中, ,且 , , 成等比数列.数列 的前n项和为 ,满足
求数列 , 的通项公式;若数列 满足 求数列 的前2n项和
18. 本小题12分
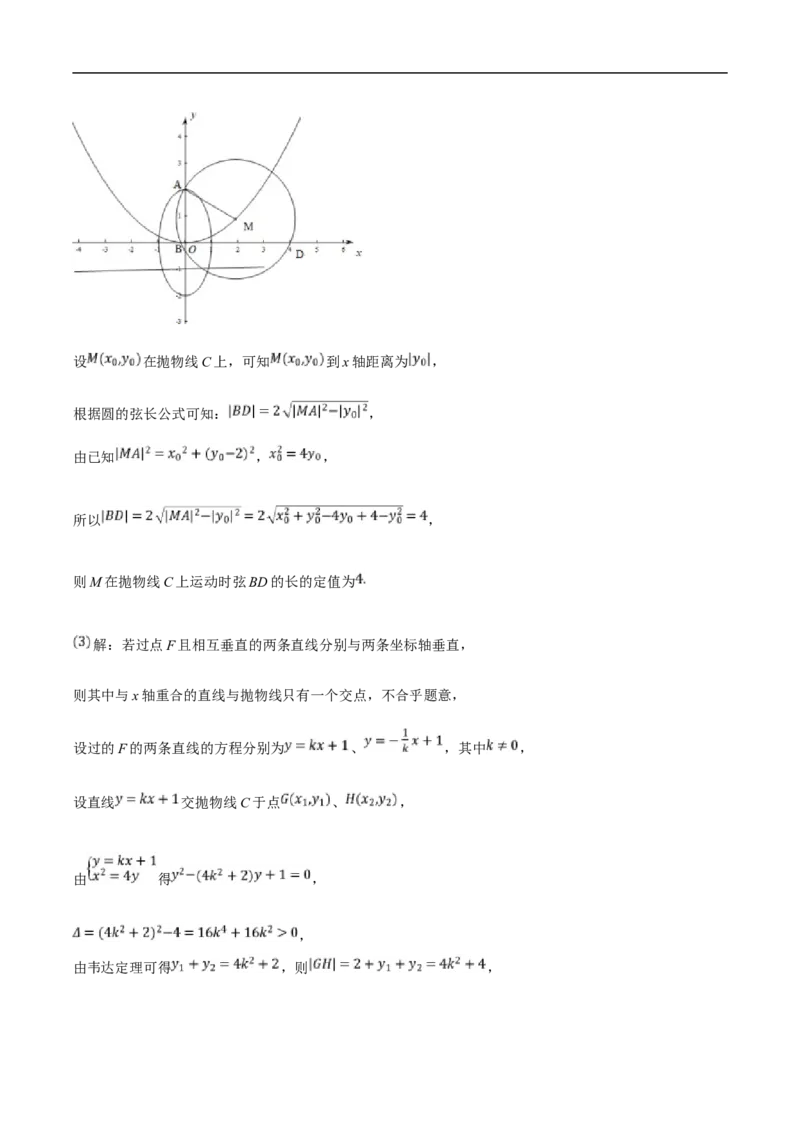
已知抛物线 的准线与椭圆 相交所得弦长为
求抛物线C的方程;
若圆M过点 ,且圆心M在抛物线C上运动,BD是圆M在x轴上截得的弦.求证:弦BD的长为定
值;
过抛物线C的焦点F作两条互相垂直的直线分别与抛物线C交于点G,H和点R,S,求四边形GRHS
面积的最小值.
19. 本小题12分
已知函数 ,
当 时,求函数 的单调区间;
若函数 在定义域内单调递增,求a的取值范围;
若函数 有两个极值点 , ,且 恒成立,求实数m的取值范围.2024-2025 学年山东省滨州市高二上学期 1 月期末数学解析
1.【答案】B
解析:
解:根据题意,椭圆的方程为 ,其焦点在y轴上,
其中 , ,
则 ,
则其焦点坐标为
2.【答案】C
解析:
解:过点 且与直线 平行的直线的方程为 ,
把点 代入 可得: ,解得 ,
要求的直线方程为:
故选:
3.【答案】D
解析:解:由题意,G是AC,BD的中点,
所以 ,
所以
4.【答案】A
解析:
解:因为 ,所以 ,
则 ,解得
5.【答案】B
解析:解:设动圆的圆心为P,半径为r,圆 的圆心为 ,半径为 ;
圆 的圆心为 ,半径为
依题意得 , ,
则 ,
所以点P的轨迹是双曲线的左支.
故选
6.【答案】D
解析:解:设5月出生的男职工退休年龄为 ,
则1965年5月出生的男职工退休年龄为 岁,
则1966年5月出生的男职工退休年龄为 岁,
所以公差为 ,
所以 是首项为 ,公差为 的等差数列,
1973年5月出生的男职工退休年龄为
那么1973年5月出生的男职工退休年龄为62岁2个月.
7.【答案】C
解析:
解:设 ,则 的面积为 ,
因为直线 到平面ABN的距离为 ,所以由等体积可得 ,
解得 ,
所以
故选
8.【答案】D
解析:
解:设椭圆的半长轴长为a,半短轴长为b,半焦距为c,
椭圆长轴在圆柱底面上的投影为圆柱底面圆直径,则 ,得a ,故A正确;
又b ,则c a b ,得 ,离心率为 ,故B正确;
P为椭圆的右顶点时,因为 ,所以 ,所以椭圆的最大张角为 ,
所以满足 的点P共有4个,故C正确;
,
所以 的最大值为16,故D错误.
故选:
9.【答案】ACD
解析:解:设公比为q,
则 ,即 ,
则 ,对于A、 ,故A正确;
对于B、 ,则 ,不是常数,
故数列 不是等比数列,故B错误;
对于C、 ,故C正确;
对于D、 ,故D正确.
10.【答案】ABD
解析:解:如图,取 的中点H,I,J,连接GH,HI,IJ,JE,由正方体性质,易得 ,
, ,故EFGHIJ六点共面对于选项A,F,G,H,I为 , , 的中点,故 ,显然 平面EFG,
故 平面EFG,A正确;
对于选项B, , , ,AC, 面 ,故 面 ,
面 , , , ,同理可证 面 , 面 ,
, , ,EF, 面EFG, , 平面EFG,B正确;
对于选项C,连接BD, , ,由于 , 平面EFG, 故 平面EFG,
同理可证 平面EFG,BD, 面 , ,故面 平面EFG,故平面EFG与平
面ABCD夹角和平面 与平面ABCD夹角大小相等,取BD中点为O, 面 , ,, 为平面 与平面ABCD的夹角,在 中, ,
, ,故C错误;
对于选项D,由于动直线 与 夹角为 ,故M在以 为轴的圆锥面上.
由正方体性质, 与平面EFG的交点为 的中点,设 到平面EFG的距离为d,则 ,截面圆
半径为 ,又因为六边形EFGHIJ内切圆半径为 ,故所截圆面
,故D正确.
综上,此题选
11.【答案】ABD
解析:解:从图象可以看出过点 的为 的图象,过点 的为导函数 的图象,
,当 时, ,故 , 在 上单调递减,
当 时, ,故 , 在 上单调递增,A、B错误;
当 时,函数 有极小值,C正确;
当 时, ,故 , 在 上单调递增,
所以当 时,函数 有极大值,D错误.
故选:
12.【答案】
解析:解:函数的导数为 ,所以在 的切线斜率为 ,
所以切线方程为 ,即
故答案为 .
13.【答案】
解析:
解:因为 是方公差为1的等方差数列,
所以 是公差为1的等差数列,
,
所以 ,
所以
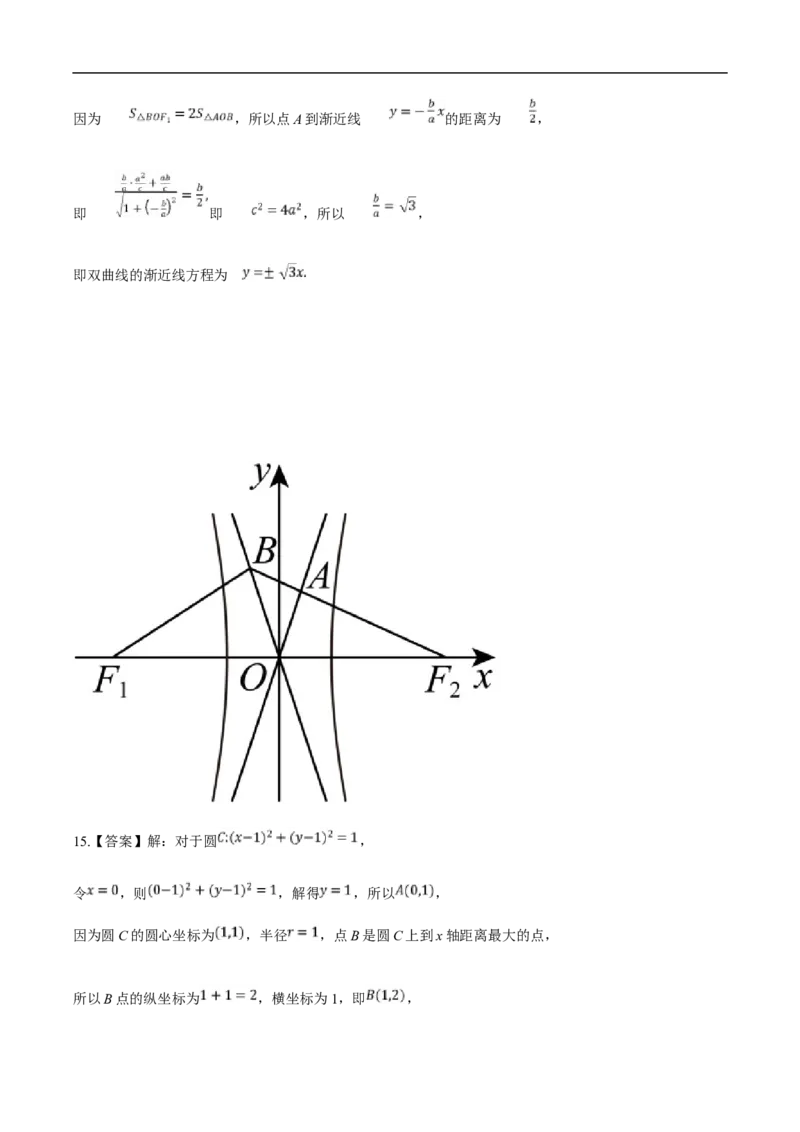
14.【答案】
解析:解:由题意知,双曲线E的两条渐近线方程分别为 , ,
过点 且与渐近线 垂直的直线方程为 ,
联立 ,可解得 ,
点 到渐近线 的距离因为 ,所以点A到渐近线 的距离为 ,
即 即 ,所以 ,
即双曲线的渐近线方程为
15.【答案】解:对于圆 ,
令 ,则 ,解得 ,所以 ,
因为圆C的圆心坐标为 ,半径 ,点B是圆C上到x轴距离最大的点,
所以B点的纵坐标为 ,横坐标为1,即 ,由直线的两点式方程可得直线AB的方程为 ,即
因为直线AB的斜率 ,因为所求直线与直线AB垂直,所以所求直线的斜率 ,
设所求直线方程为 ,即 ,
已知圆C的圆心 ,半径 ,
圆心 到直线 的距离 ,则 ,
解得 或 ,
所以所求直线方程为 或
解析:详细解答和解析过程见【答案】
16.【答案】解: 延长CB,过点A作 ,交CB延长线于点O,
由平面 平面DBC,平面 平面 , 平面ABC,
则 平面BCD,
因为 平面BCD,所以
由 , ,
则 ≌ ,
可得 , ,又 ,
得 ≌ ,则 ,
故 ,
又由 ,AO, 平面AOD,
则 平面AOD,
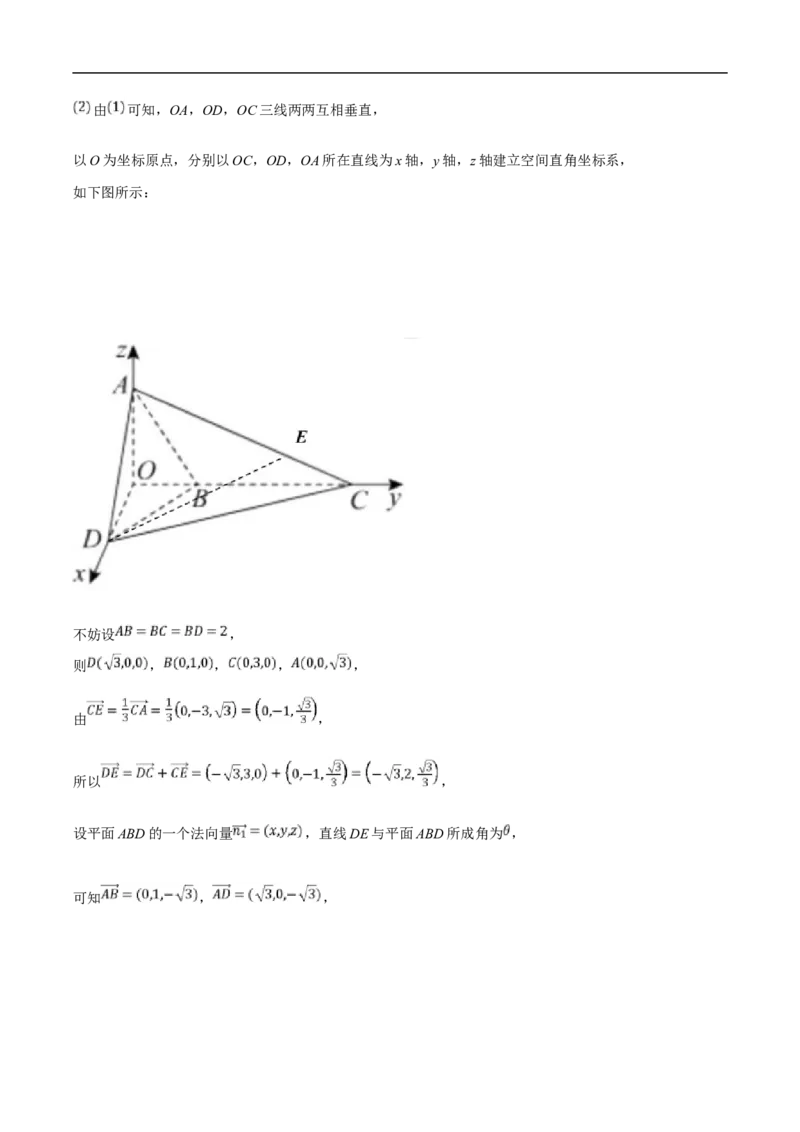
又 平面AOD,则由 可知,OA,OD,OC三线两两互相垂直,
以O为坐标原点,分别以OC,OD,OA所在直线为x轴,y轴,z轴建立空间直角坐标系,
如下图所示:
不妨设 ,
则 , , , ,
由 ,
所以 ,
设平面ABD的一个法向量 ,直线DE与平面ABD所成角为 ,
可知 , ,则 ,取 ,得 ,
所以
,
则直线DE与平面ABD所成角的正弦值为
解析:详细解答和解析过程见【答案】
17.【答案】解: 设等差数列 的公差为 ,其通项公式为 ,
已知 ,则 , ,
因为 , , 成等比数列,则 ,
即 ,
解得 或 舍去 ,
所以数列 的通项公式为
由 ①,
当 时, ,因为 ,所以 ,解得 ,
当 时, ②,
①-②得: ,
即: ,
因为 ,所以 ,即 ,
由 ,所以数列 是以 为首项,3为公比的等比数列,
所以 ,
则
综上,数列 的通项公式为 ,
数列 的通项公式为
因为 ,
所以
解析:详细解答和解析过程见【答案】
18.【答案】解: 由已知,抛物线 的准线为直线 ,与椭圆相交线段的一个端点
坐标是 ,
把 代入椭圆方程化简得 ,解得
所以抛物线C的方程为
假设M在抛物线C上运动时弦BD的长为定值,理由如下:设 在抛物线C上,可知 到x轴距离为 ,
根据圆的弦长公式可知: ,
由已知 , ,
所以 ,
则M在抛物线C上运动时弦BD的长的定值为
解:若过点F且相互垂直的两条直线分别与两条坐标轴垂直,
则其中与x轴重合的直线与抛物线只有一个交点,不合乎题意,
设过的F的两条直线的方程分别为 、 ,其中 ,
设直线 交抛物线C于点 、 ,
由 得 ,
,
由韦达定理可得 ,则 ,同理可得 ,
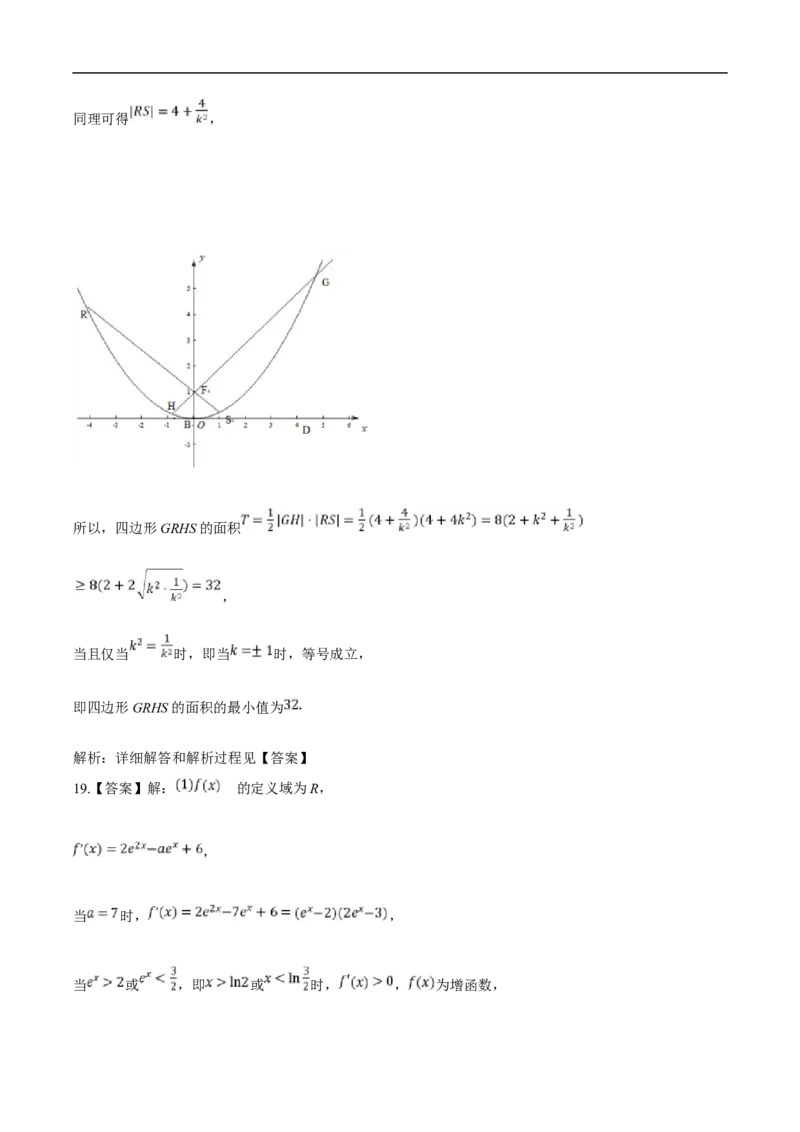
所以,四边形GRHS的面积
,
当且仅当 时,即当 时,等号成立,
即四边形GRHS的面积的最小值为
解析:详细解答和解析过程见【答案】
19.【答案】解: 的定义域为R,
,
当 时, ,
当 或 ,即 或 时, , 为增函数,当 时, , 为减函数,
故 的增区间为 , ,减区间为
由 在定义域内单调递增,
得 对任意的 恒成立,
即 恒成立,即 恒成立.
因为 ,所以 ,
当且仅当 ,即 时,等号成立,
所以 ,
即a 的取值范围是 ;
,因为函数 有两个极值点 ,
所以方程 有两个不相等的实数根 ,
故 且 ,
所以 ,
,
又 恒成立,
即 恒成立,
,设 ,
则 ,
在 上恒成立,故 在 上单调递减,
所以 ,
所以 ,
即实数m 的取值范围为
解析:详细解答和解析过程见【答案】