四川省2025届高三上学期入学摸底考试数学试题（解析版）_2024-2025高三（6-6月题库）_2024年09月试卷_0912四川省2025届新高三秋季入学摸底考试

四川省 2025 届新高三秋季入学摸底考试 数学试卷 试卷共 4页，19小题，满分 150分.考试用时 120分钟 注意事项： 1.答卷前，考生务必将自己的姓名、准考证号等填写在答题卡指定位置上. 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动， 用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上 无效. 3.考生必须保持答题卡的整洁.考试结束后，请将答题卡交回. 一、选择题：本题共 8小题，每小题 5分，共40分.在每小题给出的四个选项中，只有一项是 符合题目要求的 9−6i +2i 1. i 的虚部为（ ） A. −7 B. −6 C. −7i D. −6i 【答案】A 【解析】 【分析】根据复数的运算化简得−6−7i，再根据虚部的定义即可求解． 9−6i 9i−6i2 【详解】 +2i= +2i=−6−9i+2i=−6−7i，则所求虚部为−7. i i2 故选：A． 2. 已知等差数列 { a } 满足a =9,a =3，则a =（ ） n 3 9 12 A. −2 B. 1 C. 0 D. −1 【答案】C 【解析】 【分析】根据等差数列的通项公式求解即可. a −a 3−9 【详解】由a =9,a =3可得：d = 9 3 = =−1， 3 9 9−3 6 所以a =a +3d =3−3=0， 12 9 故选：C 第1页/共17页 学科网（北京）股份有限公司π  3. 3sin ( π−α)+sin +α  =0，则tanα=（ ） 2  3 3 3 3 A. B. C. − D. − 2 3 2 3 【答案】D 【解析】 π  sinα 【分析】利用诱导公式对 3sin ( π−α)+sin +α  =0进行化简，再利用tanα= 进行求解即可. 2  cosα π  【详解】由 3sin ( π−α)+sin +α  =0， 2  则 3sinα+cosα=0， sinα 3 因此可得tanα= =− ， cosα 3 故选：D. x2 −4x，x≥0， 4. 函数 f ( x )= 的极值点个数为（ ） −ex +1，x<0 A. 0 B. 1 C. 2 D. 3 【答案】B 【解析】 【分析】对分段函数中的每一段的函数分别探究其单调性情况，再进行综合考虑即得. 【详解】当x≥0时， f(x) = x2 −4x =(x−2)2 −4， 此时函数在[0,2]上单调递减，在[2,+∞)上单调递增，故此时函数有一个极小值点为2； 当x<0时， f(x)=−ex +1，因 f′( x )= −ex<0恒成立，故函数 f ( x ) 在(−∞,0)上单调递减， 结合函数在[0,2]上单调递减，可知0不是函数的极值点. ( ) 综上，函数 f x 的极值点只有1个. 故选：B. ( ) 5. 已知某地区高考二检数学共有8000名考生参与，且二检的数学成绩X 近似服从正态分布N 95,σ2 ， 若成绩在80分以下的有1500人，则可以估计P ( 95≤ X ≤110 )=（ ） 第2页/共17页 学科网（北京）股份有限公司5 5 11 3 A. B. C. D. 32 16 32 16 【答案】B 【解析】 3 【分析】解法一，求出P(X <80)= ，根据正态分布的对称性，即可求得答案；解法二，求出数学成绩 16 在80分至95分的人数，由对称性，再求出数学成绩在95分至110分的人数，即可求得答案. 1500 3 【详解】解法一：依题意，得P(X <80)= = ， 8000 16 1 3 5 故P ( 95≤ X ≤110 )= P ( 80≤ X ≤95 )= P(X <95)−P(X <80)= − = ； 2 16 16 解法二：数学成绩在80分至95分的有4000−1500=2500人， 由对称性，数学成绩在95分至110分的也有2500人， 2500 5 故P ( 95≤ X ≤110 )= = . 8000 16 故选：B. 6. 定义：如果集合U 存在一组两两不交（两个集合的交集为空集时，称为不交）的非空真子集 A，A，，A ( k∈N* )，且A A A =U ，那么称子集族 { A，A，，A } 构成集合U 的 一个 1 2 k 1 2 k 1 2 k k划分.已知集合I ={x∈N| x2 −6x+5<0}，则集合I 的所有划分的个数为（ ） A. 3 B. 4 C. 14 D. 16 【答案】B 【解析】 【分析】解二次不等式得到集合I ，由子集族的定义对集合I 进行划分，即可得到所有划分的个数. 【详解】依题意，I = { x∈N x2 −6x+5<0 } ={ x∈N∣1< x<5 }={ 2,3,4 } ， I 的2划分为{{2,3},{4}},{{2,4},{3}},{{3,4},{2}}，共3个， {{ } { } { }} I 的3划分为 2 , 3 , 4 ，共1个， 故集合I 的所有划分的个数为4. 故选：B. 7. 已知圆台的上､下底面的面积分别为4π,25π，侧面积为35π，则该圆台外接球的球心到上底面的距离 为（ ） 27 27 37 37 A. B. C. D. 8 4 8 4 【答案】C 第3页/共17页 学科网（北京）股份有限公司【解析】 【分析】由圆台的侧面积公式求出母线长，再由勾股定理得到高即可计算； 【详解】依题意，记圆台的上､下底面半径分别为r,r ， 1 2 则πr2 =4π,πr2 =25π，则r =2,r =5， 1 2 1 2 设圆台的母线长为l， 则π ( r +r ) l =35π，解得l =5， 1 2 则圆台的高h= 52 −( 5−2 )2 =4， 记外接球球心到上底面的距离为x， 37 则x2 +22 =( 4−x )2 +52，解得x = . 8 故选：C. 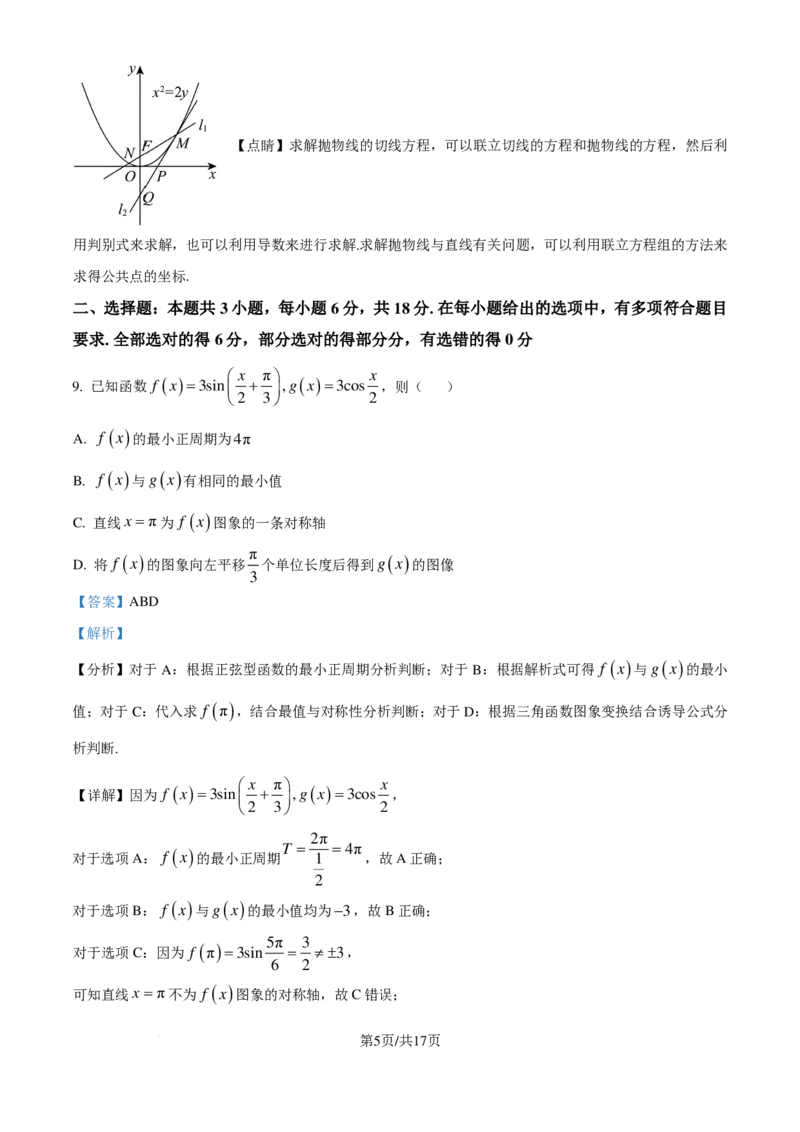8. 已知O为坐标原点，抛物线C:x2 =2py(p>0)的焦点F 到准线l的距离为1，过点F 的直线l 与C交 1   于M,N 两点，过点M 作C的切线l 与x,y轴分别交于P,Q两点，则PQ⋅ON =（ ） 2 1 1 1 1 A. B. − C. D. − 2 2 4 4 【答案】C 【解析】   【分析】通过联立方程组的方法求得P,Q的坐标，然后根据向量数量积运算求得PQ⋅ON . 1  1  x2   x2  【详解】依题意，抛物线C:x2 =2y，即y = x2，则y′= x,F0, ，设M x , 1 ,Nx , 2 ， 2  2  1 2   2 2   x2 =2y, 1  直线l : y =kx+ ，联立 1 得x2 −2kx−1=0，则x x =−1. 1 2 y =kx+ , 1 2  2 x2 x2 而直线l : y− 1 = x ( x−x )，即y = x x− 1 ， 2 2 1 1 1 2 x  x  x2  x2  令y=0，则x= 1 ，即P 1,0，令x=0，则y =− 1 ，故Q0,− 1 ， 2  2  2  2    x x2    x x x2x2 1 则PQ=− 1,− 1 ，故PQ⋅ON =− 1 2 − 1 2 = .  2 2  2 4 4 故选：C 第4页/共17页 学科网（北京）股份有限公司【点睛】求解抛物线的切线方程，可以联立切线的方程和抛物线的方程，然后利 用判别式来求解，也可以利用导数来进行求解.求解抛物线与直线有关问题，可以利用联立方程组的方法来 求得公共点的坐标. 二、选择题：本题共 3小题，每小题 6分，共18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分  x π x 9. 已知函数 f ( x )=3sin + ,g ( x )=3cos ，则（ ） 2 3 2 ( ) A. f x 的最小正周期为4π ( ) ( ) B. f x 与g x 有相同的最小值 C. 直线x = π为 f ( x ) 图象的一条对称轴 π ( ) ( ) D. 将 f x 的图象向左平移 个单位长度后得到g x 的图像 3 【答案】ABD 【解析】 ( ) ( ) 【分析】对于A：根据正弦型函数的最小正周期分析判断；对于 B：根据解析式可得 f x 与g x 的最小 ( ) 值；对于C：代入求 f π ，结合最值与对称性分析判断；对于D：根据三角函数图象变换结合诱导公式分 析判断.  x π x 【详解】因为 f ( x )=3sin + ,g ( x )=3cos ， 2 3 2 2π T = =4π ( ) 对于选项A： f x 的最小正周期 1 ，故A正确； 2 ( ) ( ) 对于选项B： f x 与g x 的最小值均为−3，故B正确； 5π 3 对于选项C：因为 f ( π )=3sin = ≠±3， 6 2 可知直线x = π不为 f ( x ) 图象的对称轴，故C错误； 第5页/共17页 学科网（北京）股份有限公司π ( ) 对于选项D：将 f x 的图象向左平移 个单位长度后， 3  π  x π x 得到 f x+  =3sin +  =3cos = g ( x ) ，故D正确.  3 2 2 2 故选：ABD. 1 10. 已知函数 f ( x )= x3−x，f′( x )为 f ( x ) 的导函数，则（ ） 3 A. f′( 0 )=0 B. f ( x ) 在 ( 1,+∞) 上单调递增 2 ( ) C. f x 的极小值为 3 1 D. 方程 f ( x )= 有3个不等的实根 2 【答案】BD 【解析】 【分析】利用导数和导数的几何意义分别判断即可. 1 【详解】因为 f ( x )= x3 −x，所以 f′( x )= x2 −1， f′( 0 )=−1，A说法错误； 3 令 f′(x)>0解得x<−1或x>1，令 f′(x)<0解得−1< x<1， 所以 f ( x ) 在 (−∞,−1 ) 单调递增，在 (−1,1 ) 单调递减，在(1,+∞)单调递增，B说法正确； 2 1 2 f ( x ) 的极大值点为x=−1，极大值 f (−1 )= > ，极小值点为x=1，极小值 f ( 1 )=− <0，C说法 3 2 3 错误； 因为当x→−∞时， f ( x )<0，当x→+∞时， f ( x )>0， 1 所以方程 f ( x )= 有3个不等的实根，分别在 (−∞,−1 ) ， (−1,1 ) 和(1,+∞)中，D说法正确； 2 故选：BD 11. 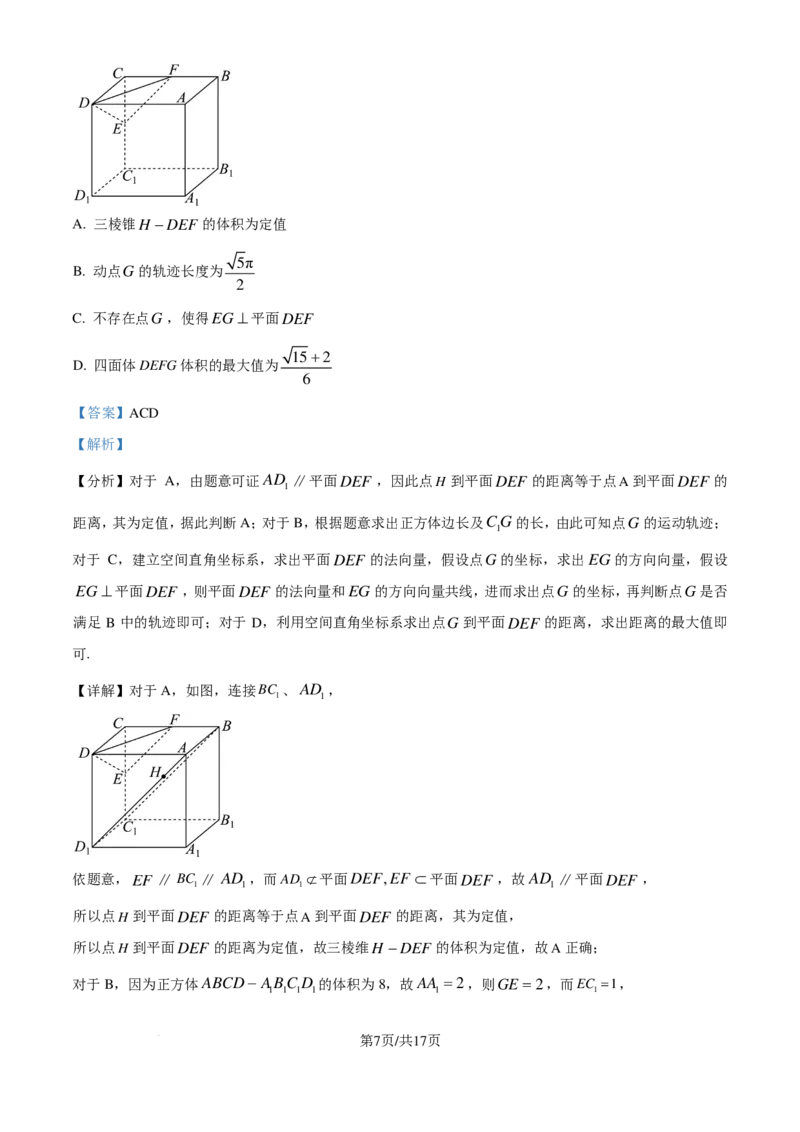已知正方体ABCD− ABC D 的体积为8，线段CC ,BC的中点分别为E,F，动点G在下底面 1 1 1 1 1 ABC D 内（含边界），动点H 在直线AD 上，且GE = AA ，则（ ） 1 1 1 1 1 1 第6页/共17页 学科网（北京）股份有限公司A. 三棱锥H −DEF 的体积为定值 5π B. 动点G的轨迹长度为 2 C. 不存在点G，使得EG ⊥平面DEF 15+2 D. 四面体DEFG体积的最大值为 6 【答案】ACD 【解析】 【分析】对于 A，由题意可证AD ∥平面DEF ，因此点H 到平面DEF 的距离等于点A到平面DEF 的 1 距离，其为定值，据此判断A；对于B，根据题意求出正方体边长及CG的长，由此可知点G的运动轨迹； 1 对于 C，建立空间直角坐标系，求出平面DEF 的法向量，假设点G的坐标，求出EG的方向向量，假设 EG ⊥平面DEF ，则平面DEF 的法向量和EG的方向向量共线，进而求出点G的坐标，再判断点G是否 满足 B 中的轨迹即可；对于 D，利用空间直角坐标系求出点G到平面DEF 的距离，求出距离的最大值即 可. 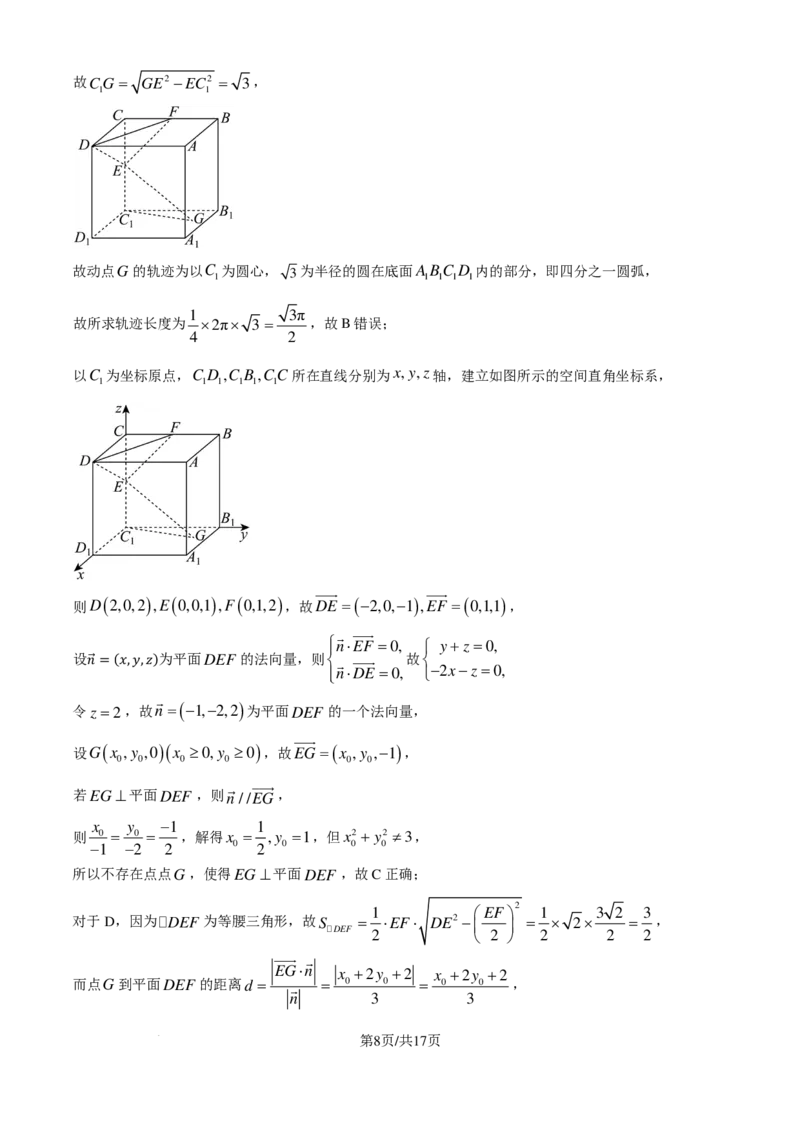【详解】对于A，如图，连接BC 、AD ， 1 1 依题意，EF ∥BC ∥ AD ，而AD ⊄平面DEF,EF ⊂平面DEF ，故AD ∥平面DEF ， 1 1 1 1 所以点H 到平面DEF 的距离等于点A到平面DEF 的距离，其为定值， 所以点H 到平面DEF 的距离为定值，故三棱维H −DEF 的体积为定值，故A正确； 对于B，因为正方体ABCD− ABC D 的体积为8，故AA =2，则GE =2，而EC =1， 1 1 1 1 1 1 第7页/共17页 学科网（北京）股份有限公司故CG = GE2 −EC2 = 3， 1 1 故动点G的轨迹为以C 为圆心， 3 为半径的圆在底面ABC D 内的部分，即四分之一圆弧， 1 1 1 1 1 1 3π 故所求轨迹长度为 ×2π× 3 = ，故B错误； 4 2 以C 为坐标原点，C D ,C B ,CC所在直线分别为x,y,z轴，建立如图所示的空间直角坐标系， 1 1 1 1 1 1   则D ( 2,0,2 ) ,E ( 0,0,1 ) ,F ( 0,1,2 ) ，故DE =(−2,0,−1 ) ,EF =( 0,1,1 )，    n⋅EF =0,  y+z =0, 设 为平面DEF 的法向量，则  故 n⋅DE =0, −2x−z =0, 𝑛𝑛�⃗=(𝑥𝑥,𝑦𝑦,𝑧𝑧)  令z =2，故n =(−1,−2,2 ) 为平面DEF 的一个法向量，  设G ( x ,y ,0 )( x ≥0,y ≥0 ) ，故EG =( x ,y ,−1 )， 0 0 0 0 0 0   若EG ⊥平面DEF ，则n//EG， x y −1 1 则 0 = 0 = ，解得x = ,y =1，但x2 + y2 ≠3， −1 −2 2 0 2 0 0 0 所以不存在点点G，使得EG ⊥平面DEF ，故C正确； 2 1  EF  1 3 2 3 对于D，因为DEF 为等腰三角形，故S = ⋅EF⋅ DE2 −   = × 2× = ， DEF 2  2  2 2 2   EG⋅n x +2y +2 x +2y +2 而点G到平面DEF 的距离d =  = 0 0 = 0 0 ， n 3 3 第8页/共17页 学科网（北京）股份有限公司 π 令x 0 = 3cosθ，则y 0 = 3sinθ,θ∈   0, 2   ， 3cosθ+2 3sinθ+2 15sin (θ+ϕ)+2 15+2 1 则d = = ≤ ，其中tanϕ= ， 3 3 3 2 1 3 15+2 15+2 则四面体DEFG体积的最大值为 × × = ，故D正确. 3 2 3 6 故选：ACD. 三、填空题：本题共 3小题，每小题 5分，共 15分     12. 已知向量a =(7,−12),b=(6,x)，若a⊥b，则x=________. 7 【答案】 2 【解析】 【分析】利用向量数量积的坐标公式计算即得.     7 【详解】由a ⊥b可得a⋅b=42−12x =0，解得，x= . 2 7 故答案为： . 2 13. 已知一组数据：3,5,7,x,9的平均数为6，则该组数据的第40百分位数为________. 【答案】5.5 【解析】 【分析】由平均数的定义算出x=6，再由百分位数的定义即可求解. 3+5+7+x+9 【详解】依题意， =6，解得x=6， 5 将数据从小到大排列可得：3,5,6,7,9， 5+6 又5×0.4=2，则40%分位数为 =5.5. 2 故答案为：5.5. 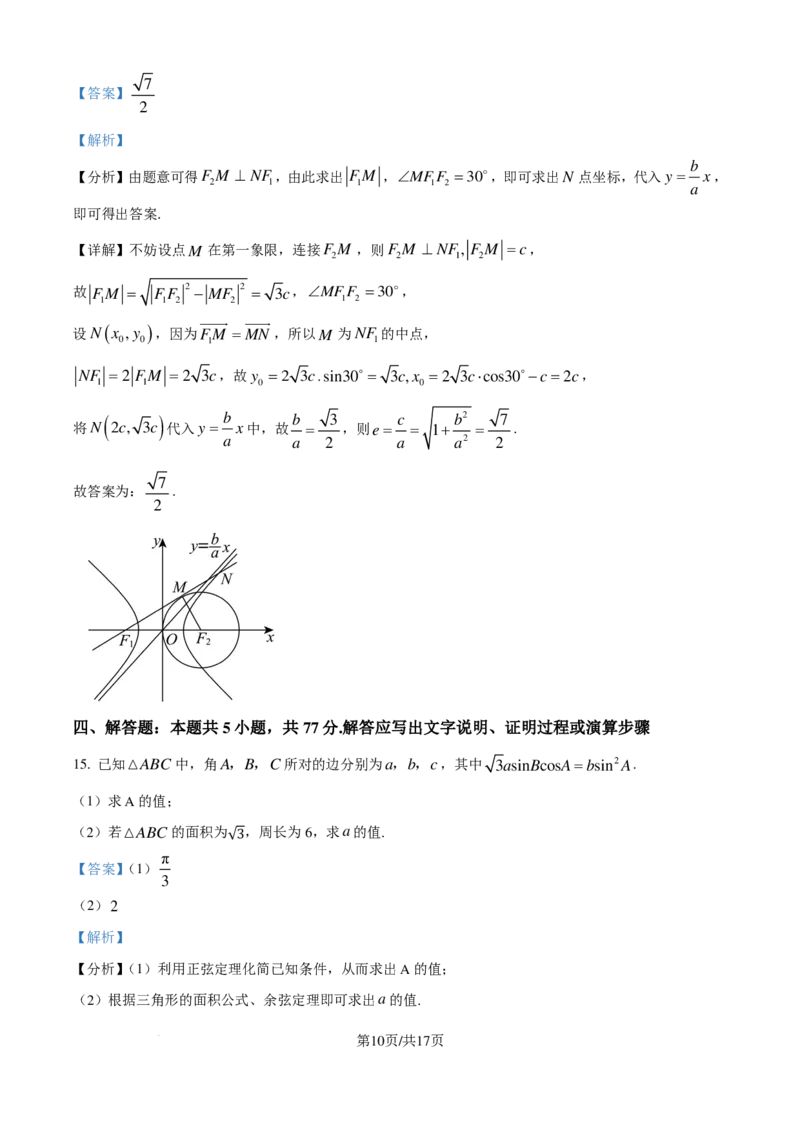x2 y2 14. 已知O为坐标原点，双曲线C: − =1(a >0,b>0)的左､右焦点分别为F,F ，点M 在以F 为 a2 b2 1 2 2 圆心､ OF 为半径的圆上，且直线MF 与圆F 相切，若直线MF 与C的一条渐近线交于点N ，且 2 1 2 1   FM =MN ，则C的离心率为__________. 1 第9页/共17页 学科网（北京）股份有限公司7 【答案】 2 【解析】 b 【分析】由题意可得F M ⊥ NF，由此求出 FM ，∠MFF =30，即可求出N 点坐标，代入y = x， 2 1 1 1 2 a 即可得出答案. 【详解】不妨设点M 在第一象限，连接F M ，则F M ⊥ NF, F M =c， 2 2 1 2 故 FM = FF 2 − MF 2 = 3c，∠MFF =30， 1 1 2 2 1 2   ( ) 设N x ,y ，因为FM =MN ，所以M 为NF 的中点， 0 0 1 1 NF =2 FM =2 3c，故y =2 3c.sin30 = 3c,x =2 3c⋅cos30 −c=2c， 1 1 0 0 ( ) b b 3 c b2 7 将N 2c, 3c 代入y = x中，故 = ，则e= = 1+ = . a a 2 a a2 2 7 故答案为： . 2 四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤 15. 已知ABC中，角A，B，C所对的边分别为a，b，c，其中 3asinBcosA=bsin2A. （1）求A的值； （2）若ABC的面积为 ，周长为6，求a的值. π 【答案】（1） √3 3 （2）2 【解析】 【分析】（1）利用正弦定理化简已知条件，从而求出A的值； （2）根据三角形的面积公式、余弦定理即可求出a的值. 第10页/共17页 学科网（北京）股份有限公司【小问1详解】 由正弦定理得 3sinAsinBcosA=sinBsin2A， 因为sinA≠0,sinB≠0，故可得 3cosA=sinA，则tanA= 3， π 因为A∈( 0,π ) ，故A= . 3 【小问2详解】 1 3 由题意S = bcsinA= bc= 3，故bc=4. ABC 2 4 由余弦定理得a2 =b2 +c2 −2bccosA=(b+c)2 −3bc=(6−a)2 −12， 解得a=2. 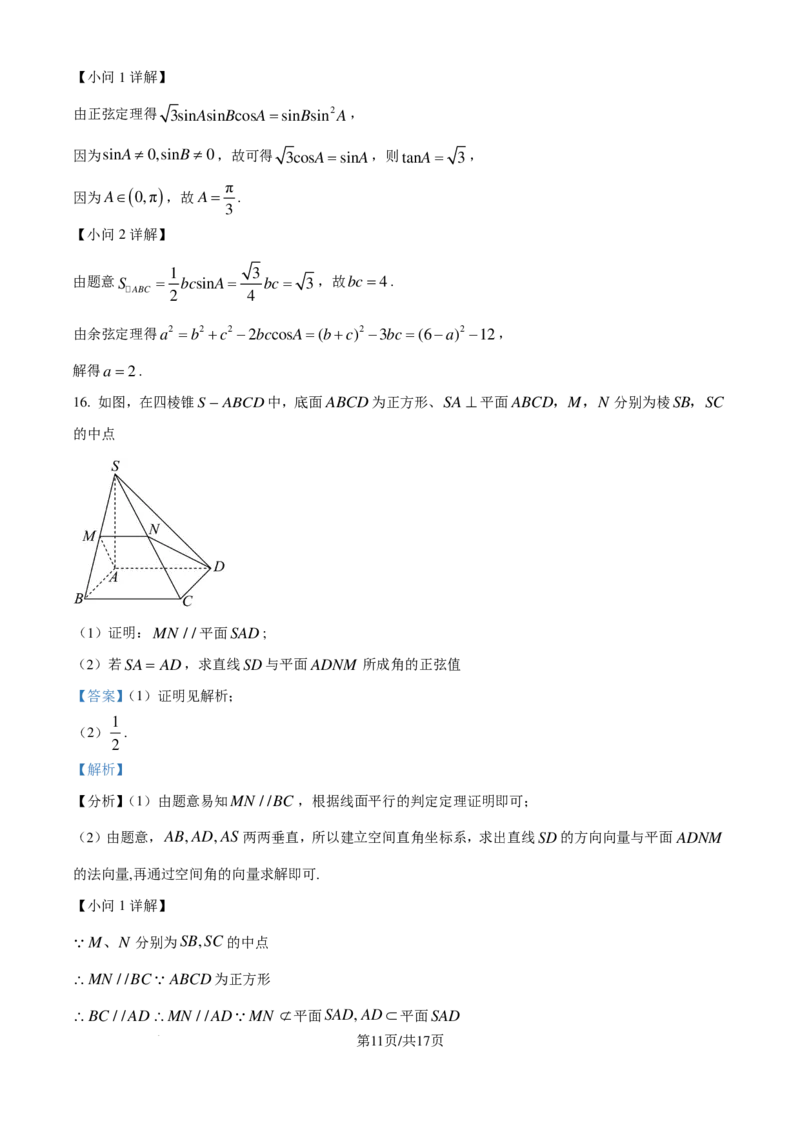16. 如图，在四棱锥S−ABCD中，底面ABCD为正方形、SA⊥平面ABCD，M，N 分别为棱SB，SC 的中点 （1）证明：MN //平面SAD; （2）若SA= AD，求直线SD与平面ADNM 所成角的正弦值 【答案】（1）证明见解析； 1 （2） . 2 【解析】 【分析】（1）由题意易知MN //BC，根据线面平行的判定定理证明即可； （2）由题意，AB,AD,AS 两两垂直，所以建立空间直角坐标系，求出直线SD的方向向量与平面ADNM 的法向量,再通过空间角的向量求解即可. 【小问1详解】 M、N 分别为SB,SC的中点 ∴MN //BCABCD为正方形 ∴BC//AD∴MN //ADMN ⊄平面SAD,AD⊂平面SAD 第11页/共17页 学科网（北京）股份有限公司∴MN / /平面SAD. 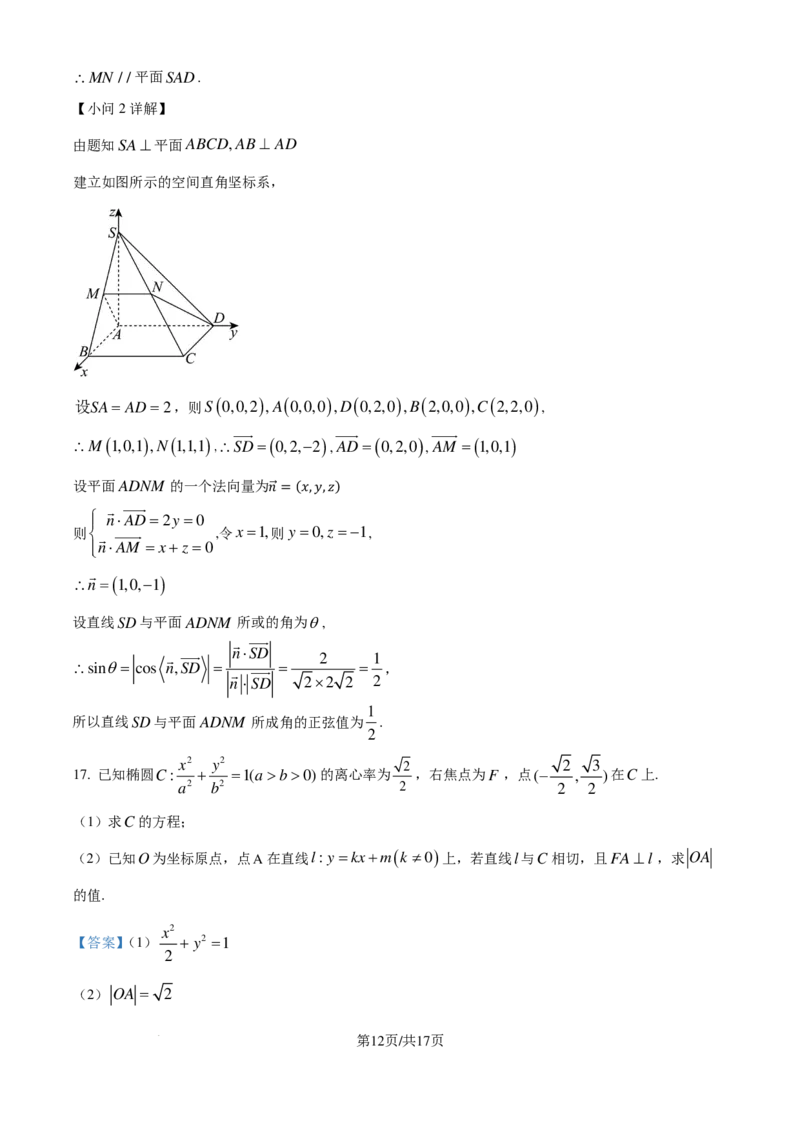【小问2详解】 由题知SA⊥平面ABCD,AB⊥ AD 建立如图所示的空间直角坚标系， 设SA= AD=2，则S ( 0,0,2 ) ,A ( 0,0,0 ) ,D ( 0,2,0 ) ,B ( 2,0,0 ) ,C ( 2,2,0 ) ,    ∴M ( 1,0,1 ) ,N ( 1,1,1 ) ,∴SD=( 0,2,−2 ) ,AD=( 0,2,0 ) ,AM =( 1,0,1 ) 设平面ADNM 的一个法向量为     n⋅AD=2y =0 𝑛𝑛�⃗=(𝑥𝑥,𝑦𝑦,𝑧𝑧) 则  ,令x=1,则y =0,z =−1, n⋅AM = x+z =0  ∴n =( 1,0,−1 ) 设直线SD与平面ADNM 所或的角为θ,     n⋅SD 2 1 ∴sinθ= cos n,SD =   = = ， n ⋅ SD 2×2 2 2 1 所以直线SD与平面ADNM 所成角的正弦值为 . 2 x2 y2 2 2 3 17. 已知椭圆C: + =1(a>b>0)的离心率为 ，右焦点为F ，点(− , )在C上. a2 b2 2 2 2 （1）求C的方程； （2）已知O为坐标原点，点A在直线l: y =kx+m(k ≠0)上，若直线l与C相切，且FA⊥l ，求 OA 的值. x2 【答案】（1） + y2 =1 2 （2） OA = 2 第12页/共17页 学科网（北京）股份有限公司【解析】 【分析】（1）根据椭圆离心率定义和椭圆上的点以及a,b,c的关系式列出方程组，解之即得； （2）将直线与椭圆方程联立，消元，根据题意，由Δ=0推得m2 =2k2 +1，又由FA⊥l ，写出直线 FA的方程，与直线l联立，求得点A坐标，计算|OA|2，将前式代入化简即得. 【小问1详解】  c 2  = a 2   1 3 设 ，依题意， + =1, 2a2 4b2  𝐹𝐹(𝑐𝑐,0)  a2 =b2 +c2   解得a2 =2,b2 =1, x2 故C的方程为 + y2 =1. 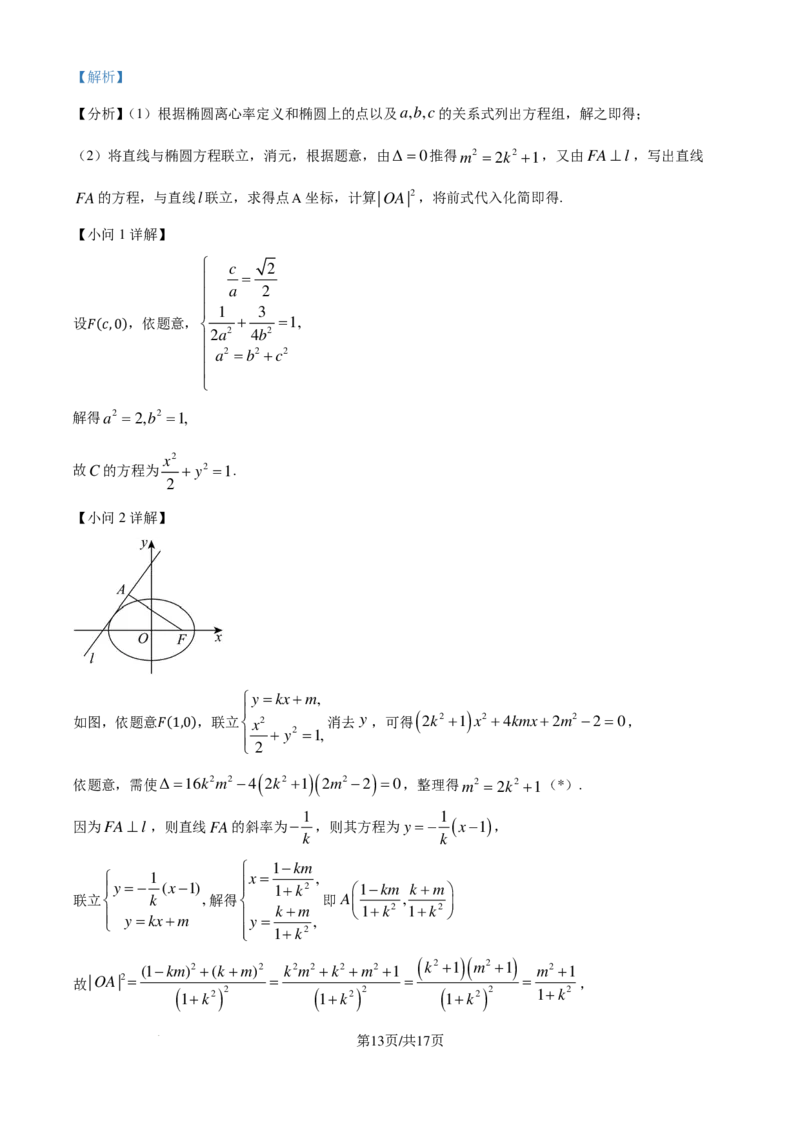2 【小问2详解】 y =kx+m,  如图，依题意 ，联立x2 消去 y，可得 ( 2k2 +1 ) x2 +4kmx+2m2 −2=0，  + y2 =1,  2 𝐹𝐹(1,0) 依题意，需使Δ=16k2m2 −4 ( 2k2 +1 )( 2m2 −2 ) =0，整理得m2 =2k2 +1（*）. 1 1 因为FA⊥l ，则直线FA的斜率为− ，则其方程为y =− ( x−1 )， k k  1−km  1 x= , y =− (x−1)   1+k2 1−km k+m 联立 k ,解得 即A ,    y =kx+m  y = k+m , 1+k2 1+k2   1+k2 ( )( ) (1−km)2 +(k+m)2 k2m2 +k2 +m2 +1 k2 +1 m2 +1 m2 +1 故|OA|2= = = = ， ( 1+k2 )2 ( 1+k2 )2 ( 1+k2 )2 1+k2 第13页/共17页 学科网（北京）股份有限公司m2 +1 2k2 +2 将（*）代入得， = =2,故 OA = 2. 1+k2 1+k2 18. 已知函数 f ( x )=lnx−x+a. （1）若a=0，求曲线 在 处的切线方程； （2）若 时 f ( x )<𝑦𝑦0=，𝑓𝑓求 (𝑥𝑥a) 的𝑥𝑥取=值1范围； 𝑥𝑥 >0 （3）若00， f(x)单调递增； 当x>1时， f′(x)<0， f(x)单调递减， 所以 f(x)≤ f(1)=−1+a，又 f(x)<0， 所以−1+a<0，即a<1， 所以a的取值范围为 (−∞,1 ) . 【小问3详解】 第14页/共17页 学科网（北京）股份有限公司由 f ( x )+x≤( x−1 ) ex−a +1可得 ( x−1 ) ex−a −lnx+1−a≥0， 即证当00，在所有 { a }( 1≤n≤4 ) 中随机抽取2个数列，记满足a <0的数列 { a } 的个数为X ，求 2 n 4 n X 的分布列及数学期望EX ； （2）若数列 { a } 满足：若存在a ≤−5，则存在k∈{ 1,2,,m−1 }( m≥2且m∈N*) ，使得 n m a −a =4. k m （i）若a >0，证明：数列 { a } 是等差数列，并求数列 { a } 的前n项和S ； 2 n n n （ii）在所有满足条件的数列 { a } 中，求使得a +2025=0成立的s的最小值. n s 【答案】（1）分布列见解析，1 （2）（i）证明见解析，S =2n2 −n（ii）1520 n 第15页/共17页 学科网（北京）股份有限公司【解析】 【分析】（1）根据递推关系化简可得a =a +4，或a =−a ,写出数列的前四项，利用古典概型即可 n+1 n n+1 n 求出分布列及期望； （2）（i）假设数列 { a } 中存在最小的整数i ( i≥3 ) ，使得a =−a ，根据所给条件 n i i−1 可推出存在k∈{ 1,2,,i−1 } ，使得a =a +4≤−1，矛盾，即可证明； k i （ii）由题意可确定−1,−5,−9,,−2017,−2021,−2025必为数列 { a } 中的项，构成新数列 { b } ，确定其通 n n 项公式及b =−2025，探求a 与b 的关系得解. 507 s n 【小问1详解】 依题意，a2 =a2 +4a +4a ，故a2 −4a +4=a2 +4a +4， n+1 n n n+1 a+1 n+1 n n 即( a −2 )2 =( a +2 )2，故a =a +4，或a =−a , n+1 n n+1 n n+1 n 因为a =1,a >0，故a =5； 1 2 2 则a :1,5,9,13;a :1,5,9,−9;a :1,5,−5,5;a :1,5,−5,−1， n n n n 故X 的可能取值为0,1,2， C2 1 C1C1 2 C2 1 故P ( X =0 )= 2 = ,P ( X =1 )= 2 2 = ,P ( X =2 )= 2 = ， C2 6 C2 3 C2 6 4 4 4 故X 的分布列为 X 0 1 2 1 2 1 P 6 3 6 1 2 1 故EX =0× +1× +2× =1. 6 3 6 【小问2详解】 （i）证明：由（1）可知，当n≥2时，a =−a 或a =a +4,a =5； n n−1 n n−1 2 假设此时数列 { a } 中存在最小的整数i ( i≥3 ) ，使得a =−a ， n i i−1 则a ,a ,,a 单调递增，即均为正数，且a ≥a =5，所以a =−a ≤−5； 1 2 i−1 i−1 2 i i−1 则存在k∈{ 1,2,,i−1 } ，使得a =a +4≤−1，此时与a ,a ,,a 均为正数矛盾， k i 1 2 i−1 第16页/共17页 学科网（北京）股份有限公司所以不存在整数i ( i≥3 ) ，使得a =−a ，故a =a +4. i i−1 n n−1 { } 所以数列 a 是首项为1､公差为4的等差数列， n n ( n−1 ) 则S =n+ ⋅4=2n2 −n. n 2 （ii）解：由a +2025=0，可得a =−2025， s s 由题设条件可得−1,−5,−9,,−2017,−2021,−2025必为数列 { a } 中的项； n 记该数列为 { b } ，有b =−4n+3 ( 1≤n≤507 ) ； n n 不妨令b =a ，则a =−a =4n−3或a =a +4=−4n+7， n j j+1 j j+1 j 均不为b =−4n−1; n+1 此时a =−4n+3或4n+1或4n−7或−4n+11，均不为b =−4n−1. j+2 s+1 上述情况中，当a =4n−3,a =4n+1时，a =−a =−4n−1=b ， j+1 j+2 j+3 j+2 n+1 结合a =1，则有a =b . 1 3n−1 n 由b =−2025可知，使得a +2025=0成立的s的最小值为3×507−1=1520. 507 s 【点睛】关键点点睛：第一问数列与概率结合，关键在于得出数列前四项的所有可能，即可按照概率问题 求解，第二问的关键在于对于新定义数列，理解并会利用一般的抽象方法推理，反证，探求数列中项的变 换规律，能力要求非常高，属于困难题目. 第17页/共17页 学科网（北京）股份有限公司