四川省成都市第七中学2024-2025学年高三上学期11月期中考试数学_2024-2025高三（6-6月题库）_2024年11月试卷_1110四川省成都市第七中学2024-2025学年高三上学期11月期中考试

2024~2025 学年度上期高 2025届半期考试 高三数学试卷 考试时间：120 分钟 总分：150 分 注意事项： 1.答卷前，考生务必将自己的姓名、班级、准考证号填写在答题卡上． 2.回答选择题时，必须使用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动， 用橡皮擦干净后，再选涂其他答案标号． 3.答非选择题时，必须使用0.5毫米黑色签字笔将答案书写在答题卡规定的位置上. 4.所有题目必须在答题卡上作答，在试题卷上作答无效． 5.考试结束后，请考生个人留存试卷并将答题卡交回给监考教师． 一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一 项是符合题目要求的 12i 1.复数 的虚部是 ( ) 34i 1 1 2 2 A. B. C.  D. 5 5 5 5 1tan15 2.式子 的值为（ ） 1tan15 A. 3 B. 2 C. 5 D. 6 3.由正数组成的等比数列 a ，S 为其前n项和，若a a 1，S 7，则S 等于（ ） n n 2 4 3 5 15 31 33 17 A. B. C. D. 2 4 4 2 4.在(1x)3  ( 1  x ) 4 (1x)n2的展开式中，含x2项的系数是（ ） A. C3 B. C2 1 C. C3 1 D. 1C3 n3 n3 n3 n3 5.已知函数 f(x) 对 xR 都有 f(x) f(4x) ，且其导函数 f(x) 满足当 x 2 时 (x2)f(x)0，则当2a4时，有( ) A. f(2a) f(2) f(log a) B. f(log a) f(2) f(2a) 2 2 C. f(log a) f(2a) f(2) D. f(2) f(log a) f(2a)  2        2 6.若向量a,b,c满足， a  b  2 c  2，则(ab)(cb)的最大值为（ ） A. 10 B. 12 C. 5 3 D. 6 2 x 2,x1 x  7.若对xR，函数 f(x) a 的函数值都不超过函数g(x) 2 的函数值， 2 x ,x1  x 则实数a的取值范围是（ ） A. a2 B. a2 C. 2a2 D. a2 8.在三棱柱ABC ABC 中 ，CACB CC ，AB  3，C 在 面 A B C 的 投 影 为  AB C 1 1 1 1 1  的外心，二面角ACC B 为 ，该三棱柱的侧面积为（ ） 1 1 3 A. 4 33 B. 7 3 C. 6 3 D. 5 3 {#{QQABZYIEggiIAAIAAAhCQQGCCACQkhAAASgOgAAMMAABSAFABAA=}#}{#{QQABZYIEggiIAAIAAAhCQQGCCACQkhAAASgOgAAMMAABSAFABAA=}#}16. （本小题满分15分） 在校运动会上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50m以上（含 9.50m）的同学将获得优秀奖．为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙 以往的比赛成绩，并整理得到如下数据（单位：m）： 甲：9.80，9.70，9.55，9.54，9.48，9.42，9.40，9.35，9.30，9.25； 乙：9.78，9.56，9.51，9.36，9.32，9.23； 丙：9.85，9.65，9.20，9.16 假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立． (I)估计甲在校运动会铅球比赛中获得优秀奖的概率； (II)设X 是甲、乙、丙在校运动会铅球比赛中获优秀奖的总人数，估计X 的数学期望E(X). 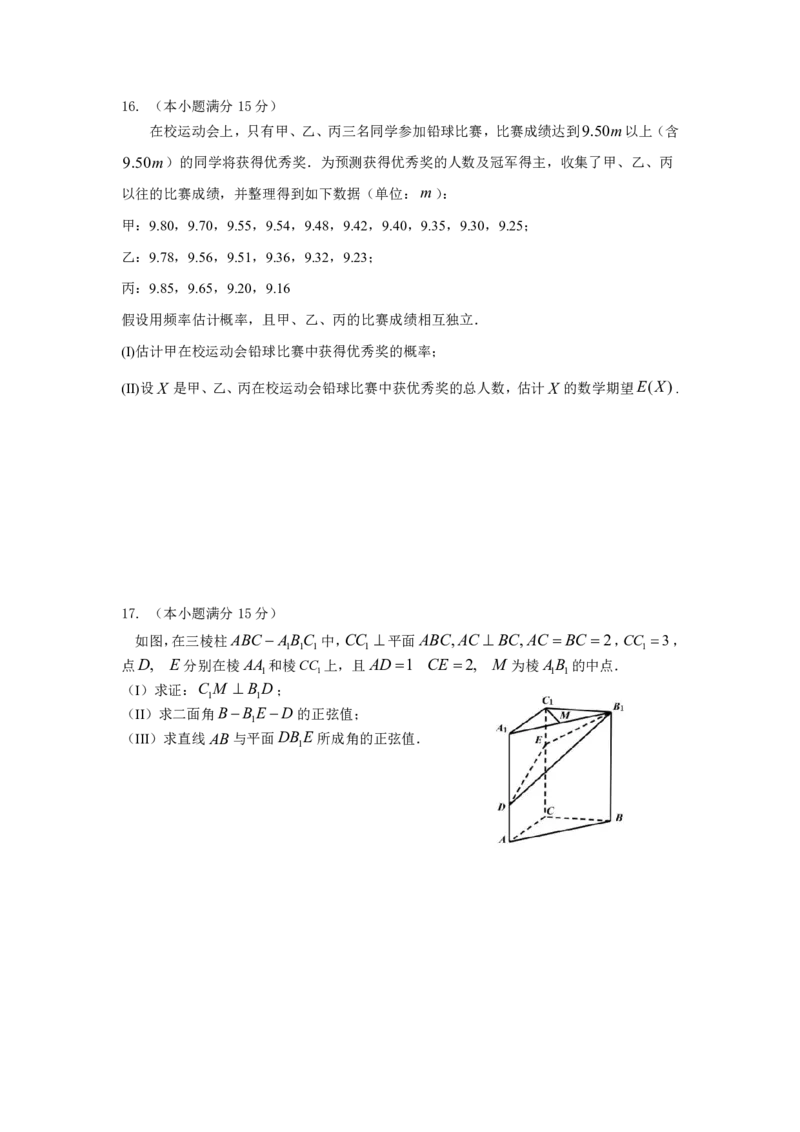17. （本小题满分15分） 如图，在三棱柱ABCABC 中，CC 平面ABC,AC BC,AC  BC 2，CC  3 ， 1 1 1 1 1 点D, E分别在棱AA 和棱CC 上，且AD1 CE 2, M 为棱AB 的中点． 1 1 1 1 （I）求证：C M  BD； 1 1 （II）求二面角BBED的正弦值； 1 （III）求直线AB与平面DBE所成角的正弦值． 1 {#{QQABZYIEggiIAAIAAAhCQQGCCACQkhAAASgOgAAMMAABSAFABAA=}#}18.（本小题满分17分） x 2 y 2 椭圆E:  1(a b0)左焦点F 和A(a,0),B(0,b)构成一个面积为2( 21) a 2 b 2 2 的FAB ,且cosAFB  . 2 （I）求椭圆E的标准方程； （II）点P是E在三象限的点，PA 与 y轴交于M ，PB与x轴交于N ①求四边形ABNM 的面积； ②求PMN 面积最大值及相应P点的坐标. 19.（本小题满分17分） 已知函数 f(x)ex ax2 x1. （其中e2.71828） （I） 当a 0时，证明： f(x)0 （II）若x0时， f(x)0，求实数a的取值范围; ex 1 23 （Ⅲ）记函数g(x) 2lnx的最小值为m，求证：m( ,e1) x 20 {#{QQABZYIEggiIAAIAAAhCQQGCCACQkhAAASgOgAAMMAABSAFABAA=}#}