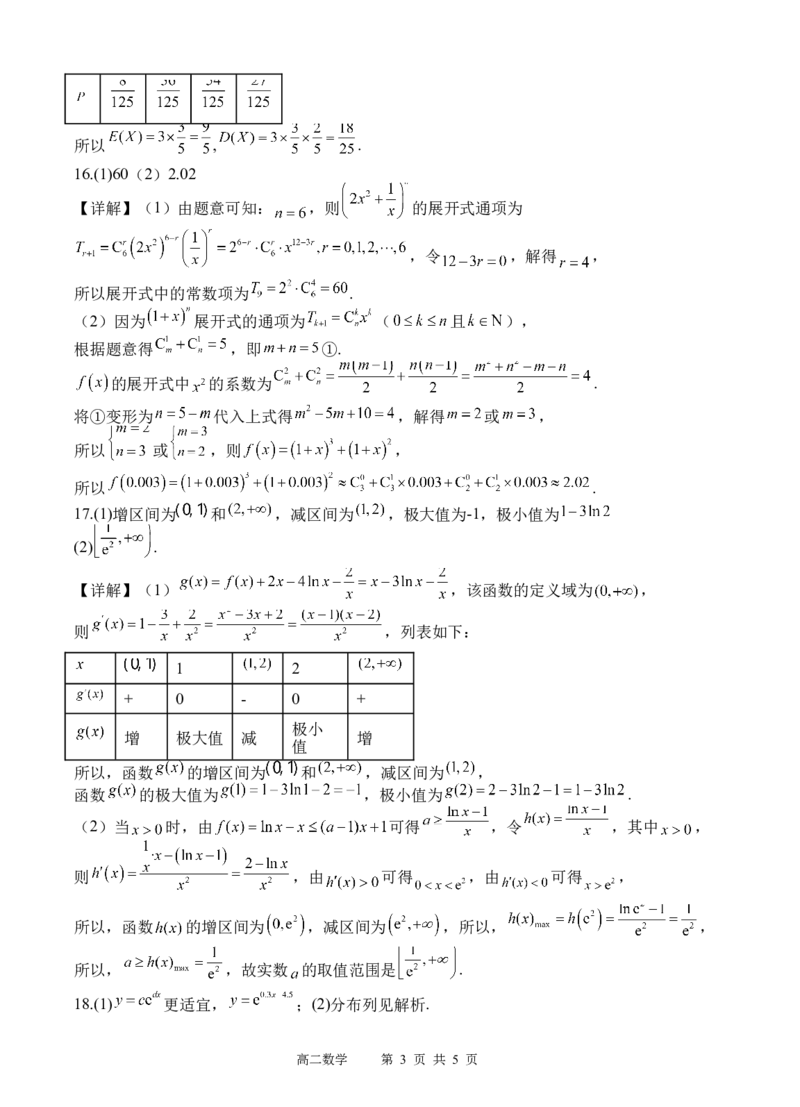文档内容
射洪中学高 2022 级高二(下)期末模拟考试
数学参考答案
1.D 2.C 3.A 4.D 5.B 6.C 7.B 8.C
【详解】对任意的 , ,且 , ,易知 ,
则 ,所以 ,即 .令
,则函数 在 上单调递减.因为 ,由 ,可得
,
所以函数 的单调递减区间为 ,所以 ,故 ,
即实数 的取值范围为 .故选:C.
9.AC 10.BCD 11.ACD
【详解】由函数 ,可得其定义域为 .A中:当 时,
,可得 ,所以 ,所以曲线 在点
处的切线方程为 ,即 ,所以A正确;B中:由
,
当 时, ,故 在 上恒成立,故函数 在 上单调递增,
无极值点,所以B错误; C中:设切点为 ,则 ,
所以曲线 在点 处的切线方程为 ,又切线过原点
,所以 ,即 ,即 ,所以
,设 ( 且 ),则 ,
当 时, ;当 时, ,
所以 在 上单调递增,在 上单调递减;当 时, ;当
时, ,且 的极大值为 , 由题意可知,函数 的图象与
直线 有两个不同的交点,可得 ,所以 ,所以 ,所以
C正确;D中:要使 有两个零点,则方程 有两个解,即方程 有两个解,
高二数学 第 1 页 共 5 页即方程 有两个解,设 ,则 ,当 时, ;当
时, ,所以 在 上单调递增,在 上单调递减,
所以 的极大值为 ,又因为 ,当 时, ,当 时,
,
所以 ,解得 ,所以D正确.故选:ACD.
12. 13.54
14. 【详解】 ,则
,
若函数 存在唯一极值点,则 在 上有唯一的根,所以由
可得 ,则 有唯一的根,直线 与函数
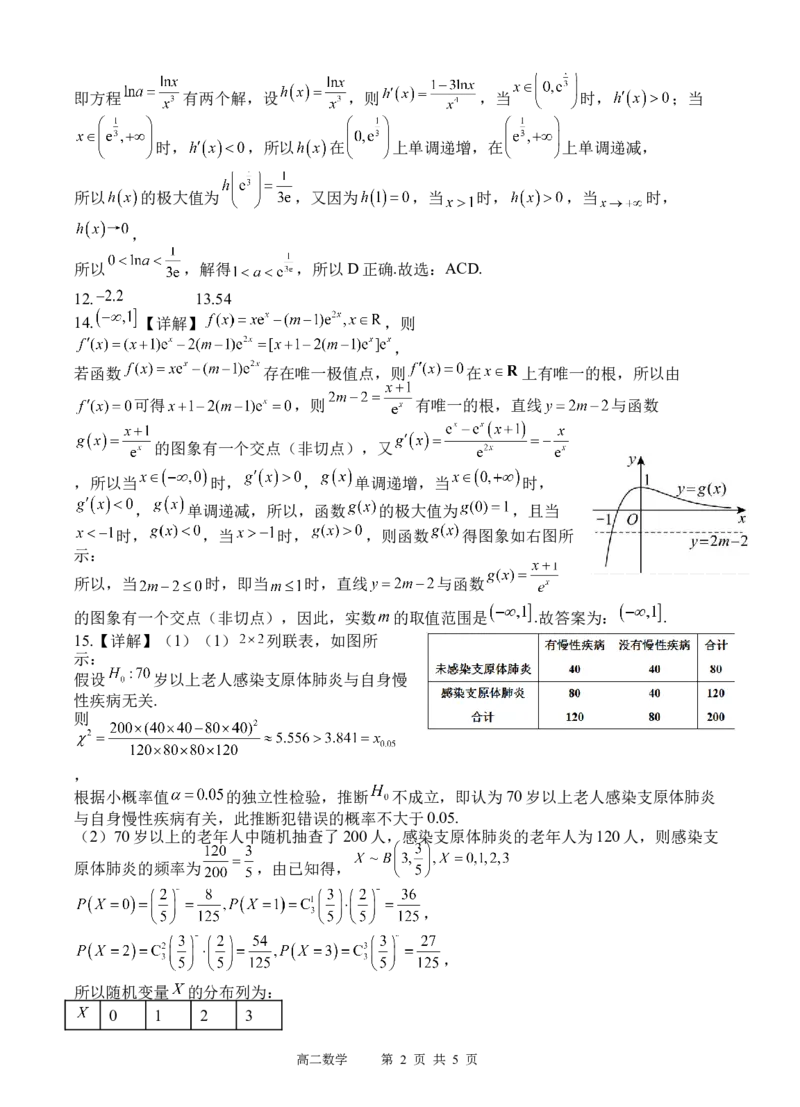
的图象有一个交点(非切点),又
,所以当 时, , 单调递增,当 时,
, 单调递减,所以,函数 的极大值为 ,且当
时, ,当 时, ,则函数 得图象如右图所
示:
所以,当 时,即当 时,直线 与函数
的图象有一个交点(非切点),因此,实数 的取值范围是 .故答案为: .
15.【详解】(1)(1) 列联表,如图所
示:
假设 岁以上老人感染支原体肺炎与自身慢
性疾病无关.
则
,
根据小概率值 的独立性检验,推断 不成立,即认为70岁以上老人感染支原体肺炎
与自身慢性疾病有关,此推断犯错误的概率不大于0.05.
(2)70岁以上的老年人中随机抽查了200人,感染支原体肺炎的老年人为120人,则感染支
原体肺炎的频率为 ,由已知得,
,
,
所以随机变量 的分布列为:
0 1 2 3
高二数学 第 2 页 共 5 页所以 , .
16.(1)60(2)2.02
【详解】(1)由题意可知: ,则 的展开式通项为
,令 ,解得 ,
所以展开式中的常数项为 .
(2)因为 展开式的通项为 ( 且 ),
根据题意得 ,即 ①.
的展开式中 的系数为 .
将①变形为 代入上式得 ,解得 或 ,
所以 或 ,则 ,
所以 .
17.(1)增区间为 和 ,减区间为 ,极大值为-1,极小值为
(2) .
【详解】(1) ,该函数的定义域为 ,
则 ,列表如下:
1 2
+ 0 - 0 +
极小
增 极大值 减 增
值
所以,函数 的增区间为 和 ,减区间为 ,
函数 的极大值为 ,极小值为 .
(2)当 时,由 可得 ,令 ,其中 ,
则 ,由 可得 ,由 可得 ,
所以,函数 的增区间为 ,减区间为 ,所以, ,
所以, ,故实数 的取值范围是 .
18.(1) 更适宜, ;(2)分布列见解析.
高二数学 第 3 页 共 5 页【详解】(1)根据散点图的形状,判断 更适宜作为平均产卵数y关于平均温度x的回
归方程类型,将 两边同时取自然对数,得 ,
依题意, , ,
因此 ,则 ,
于是z关于x的线性回归方程为 ,所以y关于x的回归方程为 .
(2)依题意,X的可能值为 , ,
,所以X的分布列为:
0 1 2 3
19.(1)证明见解析(2)证明见解析 (3)1
【详解】(1)设 ,则 ,当 时, ;当 时,
,
所以 在 上单调递减,在 上单调递增.因此 ,即 ;
(2)由泰勒公式知 ①,于是
②,由①②得
, ,
所以 ,即 ;
(3)由(2)知 ,所以当 时, ,
由此可知,当 时,有 对 恒成立,
下面证明:当 时, 对 不恒成立,
令 ,则 ,
令 ,则 ,
令 ,则 ,
令 ,即 ,
高二数学 第 4 页 共 5 页解得 或 .
因为当 时, ,故 舍去,
所以当 时, ,得 在 上单调递减,
故 ,即 ,
从而 在 上单调递减,故 ,
即 ,
因此 在 上单调递减,所以 ,矛盾,
所以当 时, 对 不恒成立,综上, 的最大值是1.
高二数学 第 5 页 共 5 页