文档内容
2023—2024 学年第一学期 10 月六校联合调研试题
高三数学
2023.10
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1. 已知集合 , ,则 ( )
A. B. C. D.
2. 设 是等比数列,且 , ,则 ( )
A. 12 B. 24 C. 30 D. 32
3. 下列求导正确的是( )
A. B.
C. D.
4. 已知角 终边上有一点 ,则 是( )
.
A 第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
5. 已知直线 和圆 交于 两点,则 的最小值为( )
A. 2 B. C. 4 D.
6. 已知样本数据 , , , , , 的平均数为16,方差为9,则另一
组数据 , , , , , ,12的方差为( ).
A. B. C. D. 77. 已知定义在 上的偶函数 满足 ,则下列说法正确的是( )
A.
B. 函数 的一个周期为2
C.
D. 函数 的图象关于直线 对称
8. 已知点 是抛物线 上不同的两点, 为抛物线的焦点,且满足 ,弦 的中
点 到直线 的距离记为 ,若不等式 恒成立,则 的取值范围( )
A. B.
C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有
多项符合题目要求全部选对的得 5分,有选错的得0分,部分选对的得2分.请把正确选项
在答题卡中的相应位置涂黑.
9. 设复数 满足 ,则下列说法错误 的是( )
A. 为纯虚数 B. 的虚部为2i
C. 在复平面内, 对应的点位于第二象限 D. =
10. 已知向量 , ,且 ,则( )
A. B.
C. 向量 与向量 的夹角是 D. 向量 在向量 上的投影向量坐标是
11. 已知函数 ,下列说法正确 的是( )A. 函数 的值域为
B. 若存在 ,使得对 都有 ,则 的最小值为
C. 若函数 在区间 上单调递增,则 的取值范围为
D. 若函数 在区间 上恰有3个极值点和2个零点,则 的取值范围为
12. 已知函数 ,则下列说法正确的是( )
A. 当 时, 在 上单调递增
B. 若 的图象在 处的切线与直线 垂直,则实数
C. 当 时, 不存在极值
.
D 当 时, 有且仅有两个零点 ,且
三、填空题:本大题共4小题,每小题5分,共20分.
13. 在 的展开式中, 的系数为______.
的
14. 2023年杭州亚运会招募志愿者,现从某高校 6名志愿者中任意选出3名,分别担任语言服务、人
员引导、应急救助工作,其中甲、乙2人不能担任语言服务工作,则不同的选法共有_______种.
15. 已知 ,若 , ,则实数 的取值范围是______.
16. 在正三棱锥 中,底面 的边长为4,E为AD的中点, ,则以D为球心,
AD为半径的球截该棱锥各面所得交线长为________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知等差数列 的前 项和为 ,且满足 , .(1)求数列 的通项公式;
(2)若数列 满足 ,求数列 的前 项和 .
18. 已知函数 ,
(1)求函数 的最值;
(2)设 的内角A,B,C的对边分别为a,b,c,若 , ,且
,求 的面积.
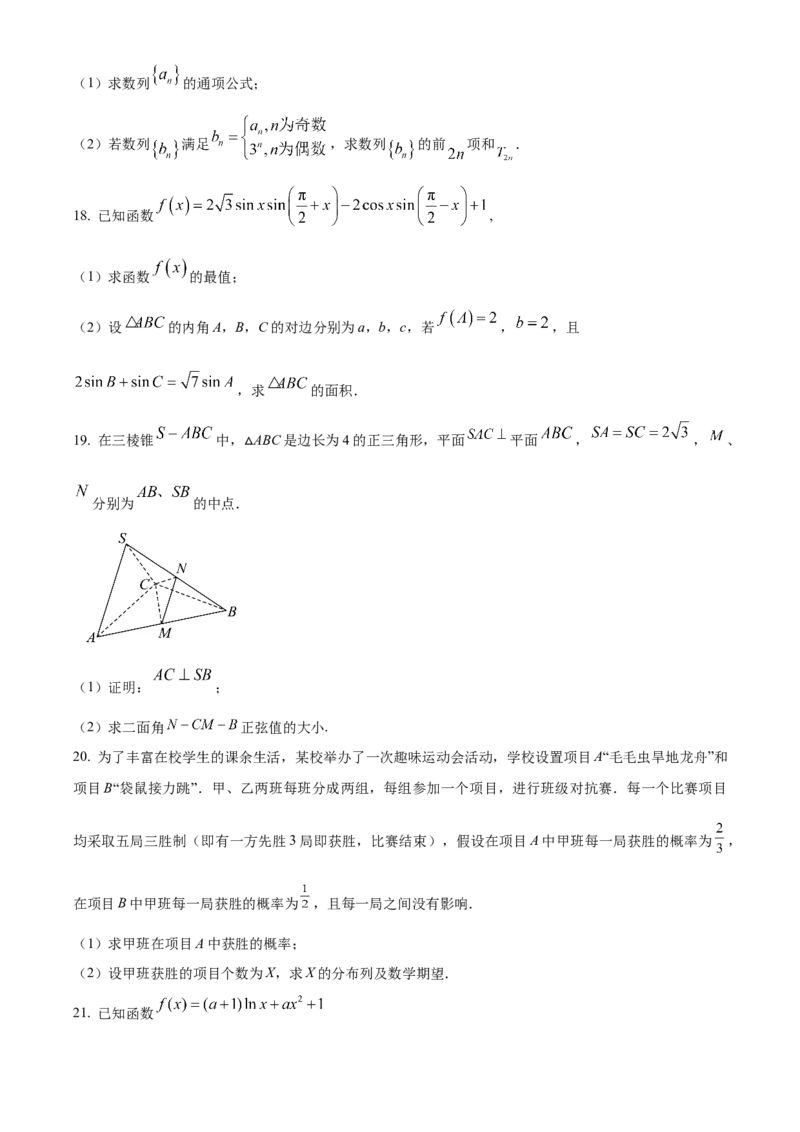
19. 在三棱锥 中, ABC是边长为4的正三角形,平面 平面 , , 、
△
分别为 的中点.
(1)证明: ;
(2)求二面角 正弦值的大小.
20. 为了丰富在校学生的课余生活,某校举办了一次趣味运动会活动,学校设置项目A“毛毛虫旱地龙舟”和
项目B“袋鼠接力跳”.甲、乙两班每班分成两组,每组参加一个项目,进行班级对抗赛.每一个比赛项目
均采取五局三胜制(即有一方先胜3局即获胜,比赛结束),假设在项目A中甲班每一局获胜的概率为 ,
在项目B中甲班每一局获胜的概率为 ,且每一局之间没有影响.
(1)求甲班在项目A中获胜的概率;
(2)设甲班获胜的项目个数为X,求X的分布列及数学期望.
21. 已知函数(1)讨论函数 的单调性;
(2)设 .如果对任意 , ,求 的取值范围.
22. 已知双曲线 过点 ,离心率 .
(1)求双曲线 的方程;
(2)过点 的直线 交双曲线 于点 , ,直线 , 分别交直线 于点 , ,求
的值.