重庆市乌江新高考协作体2024届高三下学期模拟监测（一）数学Word版含答案(1)_2024年5月_025月合集_2024届重庆市乌江新高考协作体高三下学期模拟监测（一）

重庆市乌江新高考协作体 2024 届高考模拟监测（一） 数学试题 （分数：150 分，时间：120 分钟） 一、选择题：本题共 8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项 是符合题目要求的。 1．已知集合M 0,1,2,N   x| x2 3x0  ，则M N （ ） A．0,1,2 B．1,2 C．{x∣0x3} D．{x∣0x3} 1i 2．若i为虚数单位，复数z ，则z （ ） i A．1i B．1i C．1i D．1i S 3．已知等比数列a 的前n项和为S ,a a 12且a ,a 6,a 成等差数列，则 10 为（ ） n n 1 2 1 2 3 S 5 A．245 B．244 C．242 D．241 4．洪崖洞是具有重庆特色的吊脚楼式建筑，它的屋顶可近似看作一个多面体，右图是该屋顶的结构示意图， 其中四边形ABFE和四边形DCFE是两个全等的等腰梯形，AB//CD//EF,△EAD和 是两个全等的正 三角形．已知该多面体的棱BF与平面ABCD成的角45，AB20,BC 8，则该屋△顶 的 侧 面积为（ ） A．80 B．80 3 C．160 D．160 3 51 5．数学美的表现形式多种多样，我们称离心率e（其中 ）的椭圆为黄金椭圆，现有一个黄金 2 x2 y2 椭圆方程为  1，(a b 0)，若以原点O为圆心，短轴长为直径作 为黄金椭圆上除顶点外任意 a2 b2 ⊙ , b2 a2 一点，过P作 的两条切线，切点分别为A,B，直线AB与x,y轴分别交于M,N两点，则   |OM |2 |ON|2 ⊙ （ ） 1 1 A． B． C． D．   xy20,  6．在不等式组xy20,所确定的三角形区域内随机取一点，则该点到此三角形的三个顶点的距离均大   y2, 于1的概率是（ ）     A． B．4 C．1 D．1 8 2 8 4 7．已知sin2cos与cos2sin都是非零有理数，则在sin，cos，tan中，一定是有理数的有（ ） 个. A．0 B．1 C．2 D．3 a,ab b,ab 8．定义maxa,b ,min a,b ，对于任意实数x0,y0，则 b,ab a,ab   1 1  minmax2x,3y,  的值是（ ）   4x2 9y2  A．32 B． 2 C． 3 D．33 二、多项选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符 合题目要求的。全部选对的得5分，部分选对的得2分，有选错的得2分。 9．已知a0，b0，且ab2，则（ ） 1 A．a2b2 2 B． 2ab 4 C．log alog b0 D．a2b0 4 2 2 10．已知 f xx2xlnx2，gx f xex，则（ ） 1  A．函数 f x在  ,1  上的最大值为3 B．x0， f x2 4  C．函数gx在3,4上没有零点 D．函数gx的极值点有2个 x2 11．已知双曲线C:  y2 1的左、右焦点分别为F，F ，左、右顶点分别为M ，N ，O为坐标原点， 1 2 2 直线l交双曲线C的右支于P，Q两点（不同于右顶点），且与双曲线C的两条渐近线分别交于A，B两点， 则（ ）   A．OAOB为定值 B． PA  BQC．点P到两条渐近线的距离之和的最小值为 2   D．不存在直线l使MPMQ0 三、填空题：本题共3小题，每小题5分，共15分。     12．已知正三角形ABC的边长为2，点D满足CDmCAnCB，且m0，n0，2mn1，则|CD|的 取值范围是 . 13．从教学楼一楼到二楼共有11级台阶（从下往上依次为第1级，第2级，L ，第11级），学生甲一步 能上1级或2级台阶，若甲从一楼上到二楼使用每一种方法都是等概率的，则甲踩过第5级台阶的概率 是 ． 14．若函数 f(x)xex(m1)e2x存在唯一极值点，则实数m的取值范围是 . 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。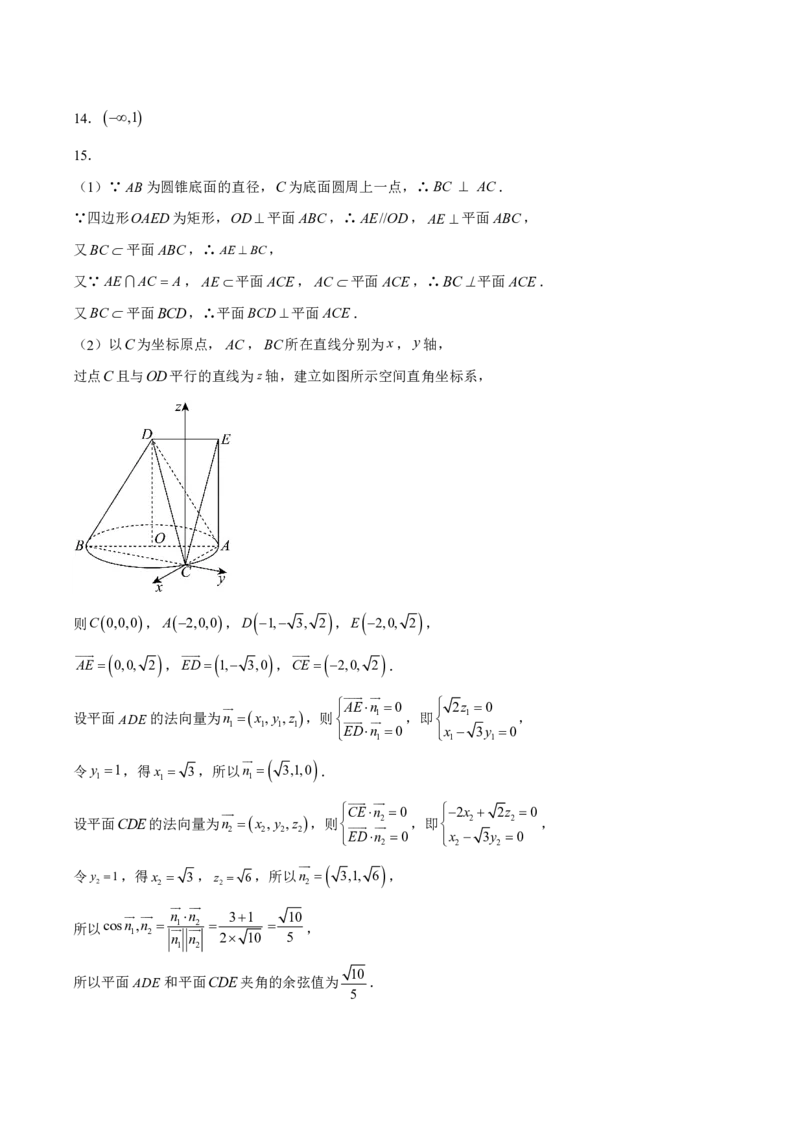 15．如图，在圆锥DO中，D为圆锥顶点，AB为圆锥底面的直径，O为底面 圆的圆心，C为底面圆周上一点，四边形OAED为矩形． (1)求证：平面BCD平面ACE； (2)若AE 2，AC2，BC2 3，求平面ADE和平面CDE夹角的余弦值. 16．已知幂函数 f xxm22m3mZ为奇函数，且在区间0,上是严格减函数. (1)求函数y f x的表达式； 1  (2)对任意实数x  ,1  ，不等式 f xt4x恒成立，求实数t的取值范围. 2 17．三峡之巅景区的索道共有三种购票类型，分别为单程上山票、单程下山票、双程上下山票．为提高服 务水平，现对当日购票的120人征集意见，当日购买单程上山票、单程下山票和双程票的人数分别为36、 60和24． (1)若按购票类型采用分层随机抽样的方法从这120人中随机抽取10人，再从这10人中随机抽取4人，求 随机抽取的4人中恰有2人购买单程上山票的概率． (2)记单程下山票和双程票为回程票，若在征集意见时要求把购买单程上山票的2人和购买回程票的m（m>2 且mN*）人组成一组，负责人从某组中任选2人进行询问，若选出的2人的购票类型相同，则该组标为 A，否则该组标为B，记询问的某组被标为B的概率为p． （i）试用含m的代数式表示p； （ii）若一共询问了5组，用gp表示恰有3组被标为B的概率，试求gp的最大值及此时m的值． 18．已知椭圆E: x2  y2 1(ab0)的左、右顶点分别为A,B,C  a, 2b  ,D  a, 2b  ，直线AC的斜率为 1 ， a2 b2 2 4 直线AC与椭圆E交于另一点G，且点G到x轴的距离为 ． 3 (1)求椭圆E的方程． (2)若点P是E上与点A,B不重合的任意一点，直线PC,PD与x轴分别交于点M,N． k k ①设直线PM,PN 的斜率分别为k ,k ，求 2 1 的取值范围． 1 2 kk 1 2 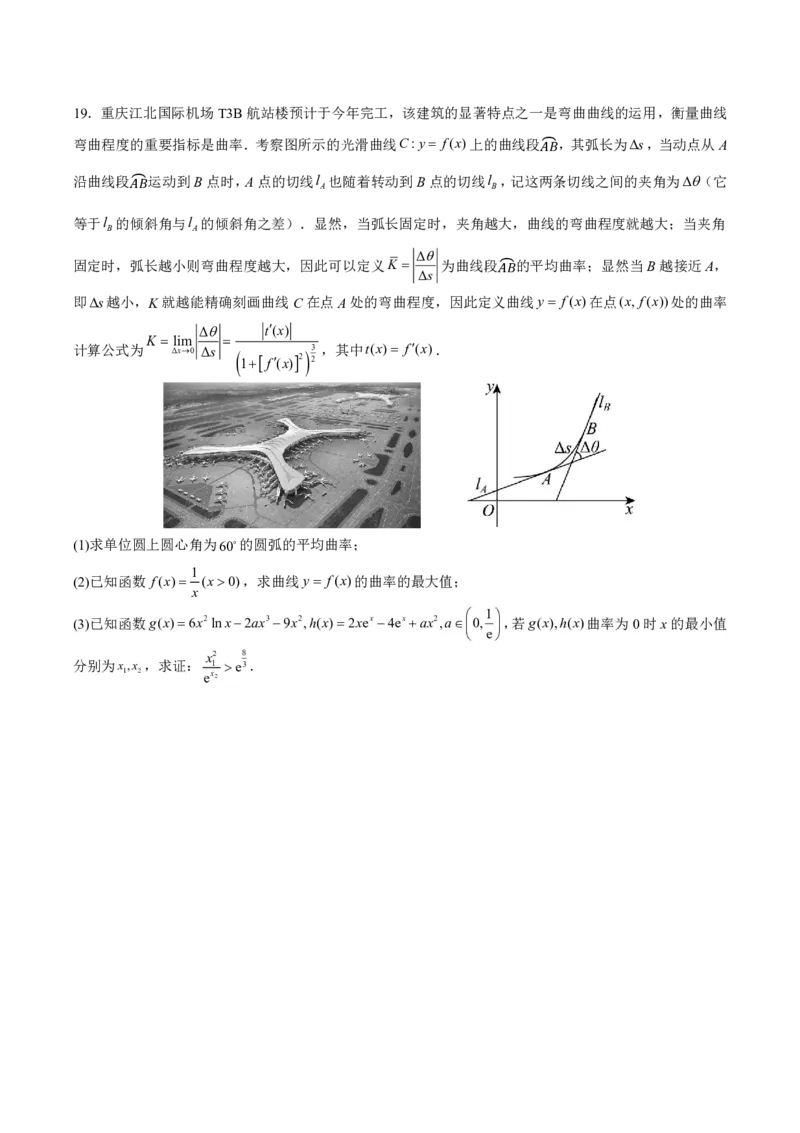②判断 AM |2  BN |2是否为定值．若为定值，求出该定值；若不为定值，说明理由．19．重庆江北国际机场T3B航站楼预计于今年完工，该建筑的显著特点之一是弯曲曲线的运用，衡量曲线 弯曲程度的重要指标是曲率．考察图所示的光滑曲线C:y  f(x)上的曲线段 ，其弧长为s，当动点从A 沿曲线段 运动到B点时，A点的切线l 也随着转动到B点的切线l ，记这两 条切线之间的夹角为（它 A B 等于l 的倾斜角与l 的倾斜角之差）．显然，当弧长固定时，夹角越大，曲线的弯曲程度就越大；当夹角 B A Δ 固定时，弧长越小则弯曲程度越大，因此可以定义K  为曲线段 的平均曲率；显然当B越接近A， Δs 即s越小，K就越能精确刻画曲线C在点A处的弯曲程度，因此定义 曲 线y f(x)在点(x, f(x))处的曲率 Δ t(x) K  lim  计算公式为 Δx0 Δs   3 ，其中t(x) f(x)． 1 f(x) 2 2 (1)求单位圆上圆心角为60的圆弧的平均曲率； 1 (2)已知函数 f(x) (x0)，求曲线y f(x)的曲率的最大值； x  1 (3)已知函数g(x)6x2lnx2ax39x2,h(x)2xex 4ex ax2,a0, ，若g(x),h(x)曲率为0时x的最小值  e x2 8 分别为x,x ，求证： 1 e3． 1 2 ex2重庆乌江新高考协作体 2024 届高考模拟监测（一） 数学答案 （分数：150 分，时间：120 分钟） 1．C 2．D 3．B 4．D 5．A 6．C 7．D【分析】令2sin+1cosm,1sin2sin1n，分别用m,n表示sin，cos，tan，进而 求得在sin，cos，tan中一定是有理数的个数. 1 1 1 1 1 8．A【分析】设max{2x,3y,  } M，则3M 2x 3y ，构造函数 f(x)x (x0)，利用导 4x2 9y2 (2x)2 (3y)2 x2 6 数求出函数 f(x)的最小值进而得3M  2 ，化简即可求解. 23 9．AB【分析】根据基本不等式可判定A，根据指数函数的单调性可判定B，根据基本不等式、对数运算 及对数函数单调性可判断C，根据二次函数的性质可判断D. 10．AC【分析】求函数 f x的导数，得 fx2xlnx1，x0.因为 fx在0,上递增，根据函数 零点的存在性判断零点在  e2,e1 之间，设为x 0 ，再代入计算可以求出函数在    1 4 ,1    上的最值，判断AB的 真假；求gx的导数，得gx2xlnx1e，x0，利用其单调性得gx0至多一解，可判断D； 再根据函数零点的存在性，可判断C的真假.     11．BD【分析】对于A，根据OAOB|OA||OB|cosAOB ，取垂直于x轴的直线，结合条件可判断A； 2km 对于B，设直线l的方程为xkym，利用韦达定理可得y y  ，联立直线与渐近线方程，可分 Q P k22 别解得y ，y ，结合弦长公式可判断B；对于C，设P(x ,y )，可得P到两渐近线距离可判断C；由题可 A B 0 0 π 得PMQ 恒成立可判断D. 2 12．1,2 13 13． 1814．,1 15． （1）∵AB为圆锥底面的直径，C为底面圆周上一点，∴BC  AC． ∵四边形OAED为矩形，OD平面ABC，∴AE//OD，AE 平面ABC， 又BC平面ABC，∴AEBC， 又∵AEAC A，AE平面ACE，AC平面ACE，∴BC平面ACE． 又BC平面BCD，∴平面BCD平面ACE． （2）以C为坐标原点，AC，BC所在直线分别为x，y轴， 过点C且与OD平行的直线为z轴，建立如图所示空间直角坐标系， 则C0,0,0，A2,0,0，D  1, 3, 2  ，E  2,0, 2  ，          AE  0,0, 2 ，ED 1, 3,0 ，CE  2,0, 2 ．     AEn 0   2z 0 设平面ADE的法向量为n x,y,z，则  1 ，即 1 ， 1 1 1 1 EDn 0 x  3y 0 1 1 1    令y 1，得x  3，所以n  3,1,0 ． 1 1 1     CEn 0  2x  2z 0 设平面CDE的法向量为n x ,y ,z ，则  2 ，即 2 2 ， 2 2 2 2 EDn 0 x  3y 0 2 2 2    令y 1，得x  3，z  6，所以n  3,1, 6 ， 2 2 2 2     n n 31 10 所以cosn ,n  1 2   ， 1 2 n n 2 10 5 1 2 10 所以平面ADE和平面CDE夹角的余弦值为 ． 516． （1）依题意 f(x)为奇函数，在区间(0,)上是严格减函数， 可得m22m30，解得1m3，由于mZ,故m0，1，2， 当m0和m2时，m22m33，此时 f(x)x3为奇函数，符合要求， 当m1时，m22m34，此时 f(x)x4为偶函数，不符合要求， f(x)x3； （2）不等式 f(x)t4x，即t x34x， 1 又 f(x)x3在(0,)上是减函数，y4x在R上为增函数，则g(x)x34x在[ ,1]上为减函数，所以 2 1 g(x) g( )6，则t6，所以实数t的取值范围为[6, )． max 2 17． （1）因为购买单程上山票、单程下山票和双程票的人数之比为3:5:2，所以这10人中，购买单程上山票、 3 5 2 单程下山票和双程票的人数分别为：10 3，10 5，10 2， 10 10 10 C2C2 3 故随机抽取的4人中恰有2人购买单程上山票的概率P 7 3  ． C4 10 10 （2）（i）从m2人中任选2人，有C2 种选法，其中购票类型相同的有C2 C2种选法，则询问的某组 m2 m 2 C2 C2 m2m2 4m 被标为B的概率p1 m 2 1  ． C2 m2 3m2 m2 3m2 m2 （ii）由题意，5组中恰有3组被标为B的概率g(p)C3p3(1 p)2 10p3(12p p2)10(p32p4 p5)， 5 所以g(p)10(3p28p35p4)10p2(p1)(5p3)，0 p1，  3 所以当 p0, 时，gp0，函数gp单调递增，  5 3  当 p ,1时，gp0，函数gp单调递减， 5  所以当 p 3 时，gp取得最大值，且最大值为g   3 C3   3  3   1 3  2  216 ． 5 5 5 5  5 625 4m 3 由 p  ，m>2且mN*，得m3． m23m2 5 216 当m3时，5组中恰有3组被标为B的概率最大，且gp的最大值为 ． 62518． 2b0 1 （1）由题意知，Aa,0．由直线AC的斜率为 1 ，得  ，所以a 2b． 2 aa 2 1 直线AC的方程为y xa．设Gs,t，则s0,t 0． 2 4 4 4 1 8 由点G到x轴的距离为 ，得t  ．由点G在直线AC上，得  sa，所以s a． 3 3 3 2 3 2 2 8  4  a   3  3 由点G在椭圆E上，得  1，解得a2．所以b 2． a2 a2 2 x2 y2 所以椭圆E的方程为  1． 4 2 （2） ①设Px ,y （ 2  y 0或0 y  2）． 0 0 0 0 y 2 y 2 由（1）知，C2,2,D2,2，则k k  0 ,k k  0 ， 1 PC x 2 2 PD x 2 0 0 k k 1 1 x 2 x 2 4 4 所以 2 1    0  0   ． kk k k y 2 y 2 y 2 2 y 1 2 1 2 0 0 0 0 由 2  y 0或0 y  2， 0 0 得2 2 2 y 2或22 y 2 2， 0 0 4 4 所以42 2  2或2 42 2． 2 y 2 y 0 0 k k   故 2 1 的取值范围是42 2,2  2,42 2．   kk 1 2 ②由①知 x 0 2  y 0 2 1，即x2 y2 4 y2．设Mx,0,Nx ,0．因为P,C,M 三点共线， 0 0 0 1 2 4 2 y 2 02 2x 4 2y 2x 所以 0  ，得x  0 2 0 0 ． x 2 x 2 1 y 2 y 2 0 1 0 0y 2 02 因为P,D,N 三点共线，所以 0  ， x 2 x 2 0 2 2x 4 2x 2y 得x  0 2 0 0 ． 2 y 2 y 2 0 0 2y 2x  2 2x 2y  2 8x28y2 16y 所以 AM 2 BN 2 x 1 22x 2 22   y 0 0 2 0 2    y 0 0 2 0 2   y 0 0 22 0  y 0  0 2 8 8  4y2 16y 82 y 2y  16y 82y  16y 0  0 8 0 0  0 8 0  0 816． y 22 y 2 y 22 y 2 y 2 y 2 0 0 0 0 0 0 故 AM |2  BN |2为定值16． 19． π π π （1）易知单位圆上圆心角为60的圆弧 ,s 1 ， 3 3 3 π Δ 3 根据定义可得平均曲率K   1 Δs π 3 1 1 （2）由 f(x) (x0)可得 f(x) ， x x2 2 又t(x) f(x)可得t(x) ；所以 x3 2 Δ t(x) x3 2 2 2 K  lim      Δx0 Δs  1f(x)2 3 2     1     x 1 2    2     3 2 x3    1 x 1 4    3 2  x2 3 2    1 x 1 4    3 2    x2 x 1 2    3 2 ， 1 1 1 易知x2 2 x2 2，当且仅当x2  时，即x1时等号成立； x2 x2 x2 2 2 2 2 K     所以 3 3 2 2 2 ，  1 2 22 x2   x2  2 即曲线y f(x)的曲率的最大值为 . 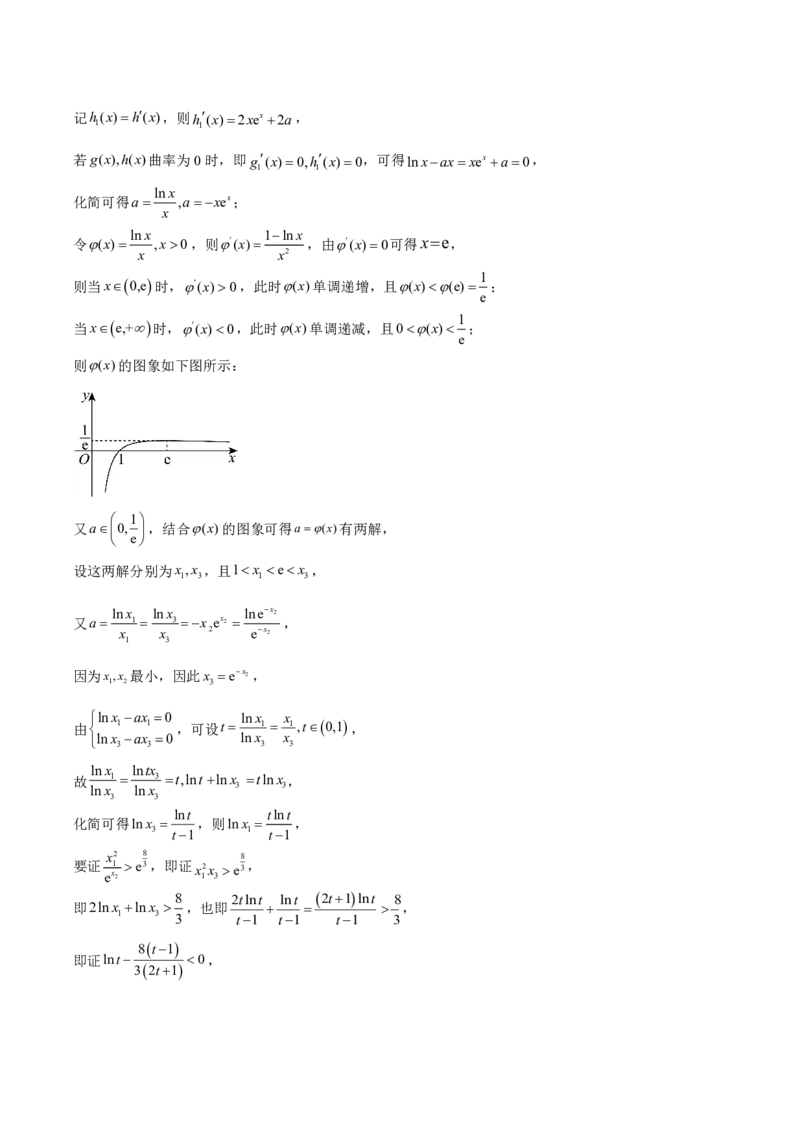2 （3）由g(x)6x2lnx2ax39x2可得g(x)12xlnx6ax218x， 记g (x)g(x)，则g  (x)12lnx12ax； 1 1 同理由h(x)2xex4exax2可得h(x)2x1ex4ex2ax，记h(x)h(x)，则h  (x)2xex2a， 1 1 若g(x),h(x)曲率为0时，即g  (x)0,h  (x)0，可得lnxaxxexa0， 1 1 lnx 化简可得a ,axex； x lnx 1lnx 令(x) ,x0，则(x) ，由(x)0可得xe， x x2 1 则当x0,e时，(x)0，此时(x)单调递增，且(x)(e) ； e 1 当xe,+时，(x)0，此时(x)单调递减，且0(x) ； e 则(x)的图象如下图所示：  1 又a0, ，结合(x)的图象可得a(x)有两解，  e 设这两解分别为x,x ，且1x ex ， 1 3 1 3 lnx lnx lnex2 又a 1  3 x ex2  ， x x 2 ex2 1 3 因为x,x 最小，因此x ex2， 1 2 3 lnx ax 0 lnx x 由 1 1 ，可设t  1  1 ,t0,1， lnx ax 0 lnx x 3 3 3 3 lnx lntx 故 1  3 t,lnt lnx tlnx， lnx lnx 3 3 3 3 lnt tlnt 化简可得lnx  ，则lnx  ， 3 t1 1 t1 x2 8 8 要证 1 e3，即证 x2x e3 ， ex2 1 3 8 2tlnt lnt 2t1lnt 8 即2lnx lnx  ，也即    ， 1 3 3 t1 t1 t1 3 8t1 即证lnt 0， 32t18t1 1 8 2t128t 2t12 令m(t)lnt ，则m(t)    0 ， 32t1 t 2t12 t2t12 t 2t12 所以m(t)在在区间t0,1上单调递增， x2 8 故m(t)m(1)0，故 1 e3. ex2