2005年上海高考数学试卷（理）（自主命题）（解析卷）_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_上海

绝密★启用前 2005年普通高等学校招生全国统一考试（上海卷） 数学试卷（理工农医类） （满分150分，考试时间120分钟） 考生注意 1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页. 2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答 题纸指定位置. 3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答 一律不得分. 4.用2B铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题. 一、填空题（41248） 1.函数 f xlog x1的反函数 f 1x________________ 4 2.方程4x 2x 20的解是___________________   3.直角坐标平面xOy中，若定点A1,2与动点Px,y满足OPOA4，则点P的轨迹方 程是______________ 4.在xa10 的展开式中，x7的系数是15，则实数a ______________   5.若双曲线的渐近线方程为y 3x，它的一个焦点是 10,0 ，则双曲线的方程是____ x12cos 6.将参数方程 （为参数）化为普通方程，所得方程是______  y 2sin 3n12n 7.计算：lim ______________ n3n 2n1 8.某班有50名学生，其15人选修A课程，另外35人选修B课程从班级中任选两名学生，他们 是选修不同课程的学生的概率是____________（结果用分数表示） 9.在ABC中，若A120，AB5，BC 7，则ABC的面积S=_________ 10.函数 f xsinx2 sinx x0,2的图像与直线y k又且仅有两个不同的交点 ，则k的取值范围是____________ 2 11.有两个相同的直三棱柱，高为 ，底面三 a 角形的三边长分别为3a、4a、5a a 0 2 2 用它们拼成一个三棱柱或四棱柱，在所有可 能的情形中，全面积最小的一个是四棱柱， a 4a 3a a 4a 3a 则a的取值范围是_______ 5a 5a 12.用n个不同的实数a ,a , ,a 可得到n!个 1 2  n 不同的排列，每个排列为一行写成一个n!行的数阵对第i行a ,a , ,a ，记 1 2 3 i1 i2  in   b i a i1 2a i2 3a i3   1n na in  1 3 2  2 1 3 i 1,2,3, ,n!例如：用1，2，3可得数阵如下，由于此数阵中每一列各数之    2 3 1   3 1 2     3 2 1 第1页 | 共8页和都是12，所以，b b  b 1221231224那么，在用1，2，3，4，5 1 2  6 形成的数阵中，b b  b ___________________ 1 2  120 二、选择题（4416） 1 13.若函数 f x ，则该函数在,上是 2x 1 (A)单调递减无最小值 (B)单调递减有最小值 (C)单调递增无最大值 (D)单调递增有最大值  5    14.已知集合M  x x1 2,xR ，Px 1,xZ，则M  P等于  x1      (A) x 0 x3,xZ (B) x 0 x3,xZ     (C) x 1 x0,xZ (D) x 1 x0,xZ 15.过抛物线y2 4x的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于 5，则这样的直线 (A)又且仅有一条 (B)有且仅有两条 (C)有无穷多条 (D)不存在 lg x1 ,x1 16.设定义域为为R的函数 f x ，则关于x的方程  0, x1 f 2xbf xc0有7个不同的实数解得充要条件是 (A)b0且c0 (B)b0且c0 (C)b0且c0 (D)b0且c0 三、解答题 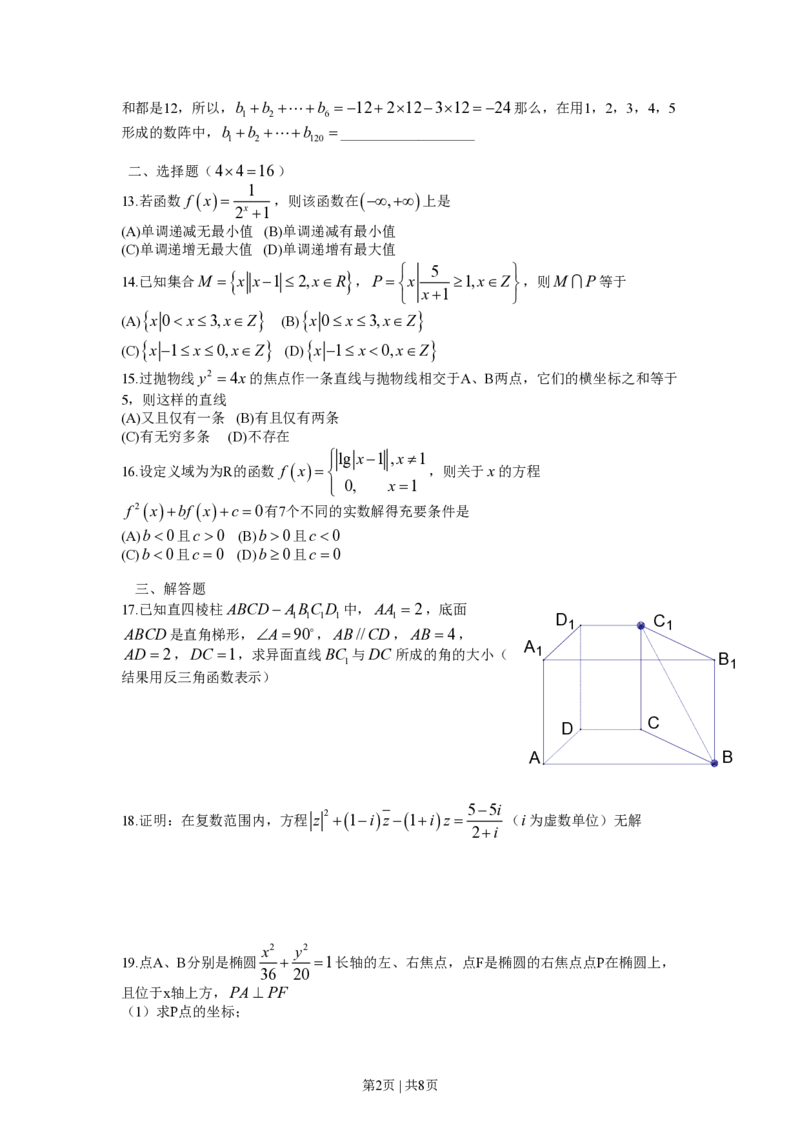17.已知直四棱柱ABCDABC D 中，AA 2，底面 1 1 1 1 1 D C 1 1 ABCD是直角梯形，A90，AB//CD，AB4， A AD2，DC 1，求异面直线BC 与DC 所成的角的大小（ 1 B 1 1 结果用反三角函数表示） C D A B 55i 18.证明：在复数范围内，方程 z 2 1iz1iz  （i为虚数单位）无解 2i x2 y2 19.点A、B分别是椭圆  1长轴的左、右焦点，点F是椭圆的右焦点点P在椭圆上， 36 20 且位于x轴上方，PA PF （1）求P点的坐标； 第2页 | 共8页（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于 MB ，求椭圆上的点到点M的 距离d的最小值 y P 3 2 1 A o M F B x -1 -2 -3 20.假设某市2004年新建住房400万平方米，其中有250万平方米是中低价房预计在今后的若 干年内，该市每年新建住房面积平均比上一年增长8%，另外，每年新建住房中，中低价房 的面积均比上一年增加50万平方米那么，到那一年底， （1）该市历年所建中低价房的累计面积（以2004年为累计的第一年）将首次不少于4750万 平方米？ （2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？ 21.（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分8分，第3小题 满分6分 对定义域是D .D 的函数y  f(x).y  g(x)， f g f(x)g(x), 当xD 且xD f g  规定：函数h(x)   f(x), 当xD 且xD f g  g(x), 当xD 且xD  f g 1 （1）若函数 f(x)  ，g(x)  x2，写出函数h(x)的解析式； x1 （2）求问题（1）中函数h(x)的值域；   （3）若g(x)  f(x)，其中是常数，且 0, ，请设计一个定义域为R的 函数y  f(x)，及一个的值，使得h(x) cos4x，并予以证明 第3页 | 共8页22.在直角坐标平面中，已知点P1,2，P  2,22 ，P  3,23 ， ,P  n,2n ，其中n是 1 2 3  n 正整数对平面上任一点A ，记A为A 关于点P的对称点，A 为A关于点P 的对称点， 0 1 0 1 2 1 2 , A 为A 关于点P 的对称点  n n1 n  （1）求向量A A 的坐标； 0 2 （2）当点A 在曲线C上移动时，点A 的轨迹是函数y  f x的图像，其中 f x是以3 0 2 位周期的周期函数，且当x0,3时， f xlgx求以曲线C为图像的函数在1,4上的 解析式；  （3）对任意偶数n，用n表示向量A A 的坐标 0 n 第4页 | 共8页2005年高考理科数学 上海卷 试题及答案 参考答案 1 y2 1. 4x 1 2. x=0 3. x+2y－4=0 4. － 5. x2  1 2 9 3 15 3 6. (x1)2  y2 4 7. 3 8. 9. 10. 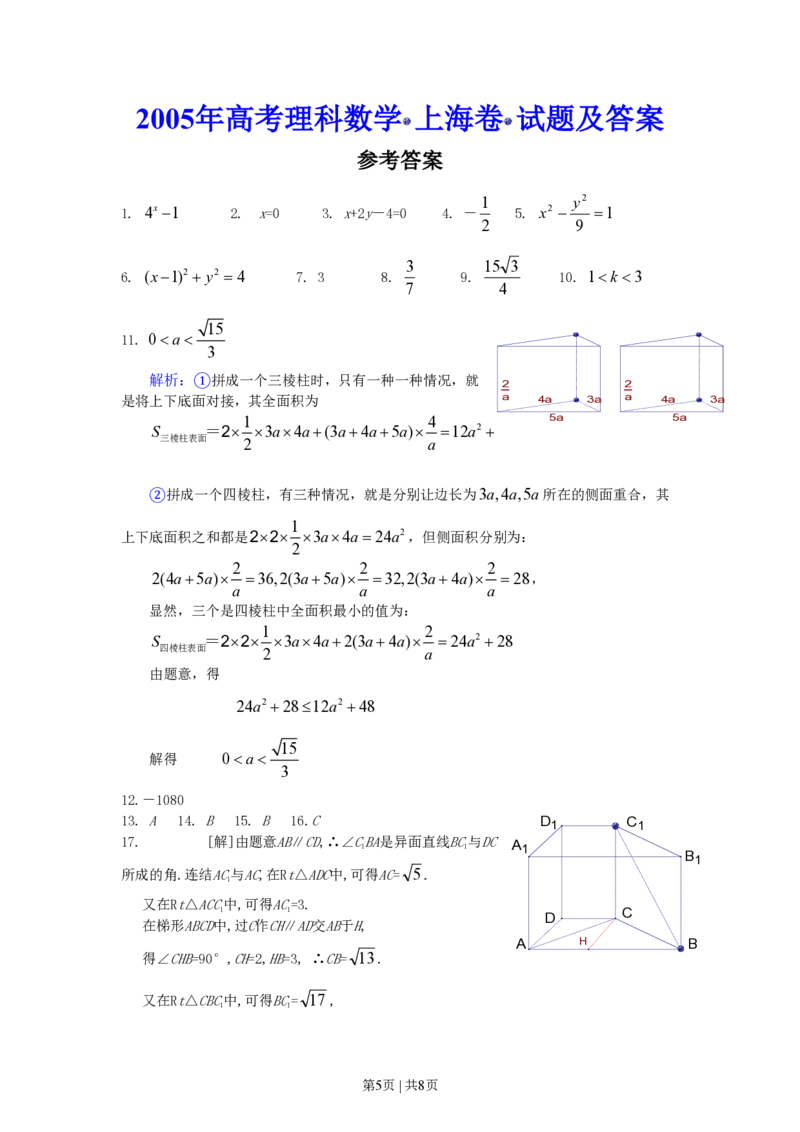1k 3 7 4 15 11. 0a 3 解析：①拼成一个三棱柱时，只有一种一种情况，就 2 2 是将上下底面对接，其全面积为 a 4a 3a a 4a 3a 1 4 5a 5a S ＝2 3a4a(3a4a5a) 12a2 48 三棱柱表面 2 a ②拼成一个四棱柱，有三种情况，就是分别让边长为3a,4a,5a所在的侧面重合，其 1 上下底面积之和都是22 3a4a24a2，但侧面积分别为： 2 2 2 2 2(4a5a) 36,2(3a5a) 32,2(3a4a) 28， a a a 显然，三个是四棱柱中全面积最小的值为： 1 2 S ＝22 3a4a2(3a4a) 24a2 28 四棱柱表面 2 a 由题意，得 24a2 2812a2 48 15 解得 0a 3 12.－1080 13. A 14. B 15. B 16.C D C 1 1 17. [解]由题意AB∥CD,∴∠CBA是异面直线BC与DC A 1 1 1 B 1 所成的角.连结AC与AC,在Rt△ADC中,可得AC= 5. 1 又在Rt△ACC中,可得AC=3. 1 1 C D 在梯形ABCD中,过C作CH∥AD交AB于H, A H B 得∠CHB=90°,CH=2,HB=3, ∴CB= 13. 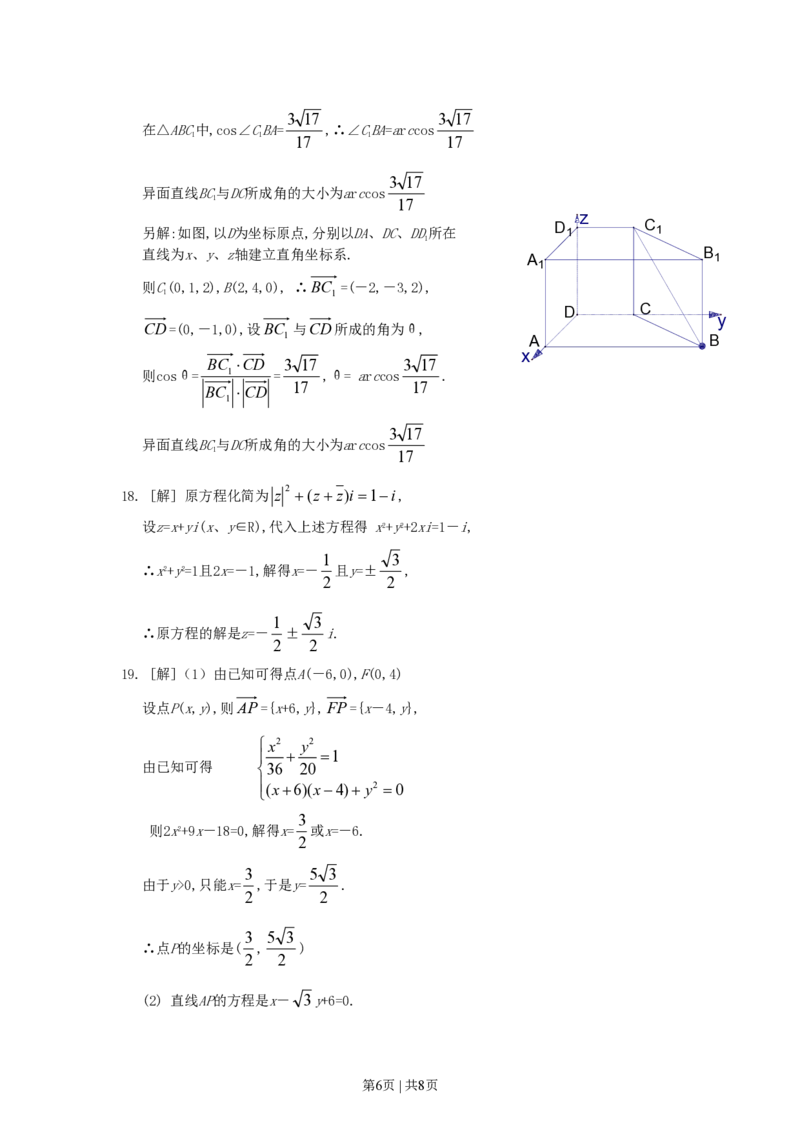又在Rt△CBC中,可得BC= 17 , 1 1 第5页 | 共8页3 17 3 17 在△ABC中,cos∠CBA= ,∴∠CBA=arccos 1 1 1 17 17 3 17 异面直线BC与DC所成角的大小为arccos 1 17 z 另解:如图,以D为坐标原点,分别以DA、DC、DD所在 D 1 C 1 1 直线为x、y、z轴建立直角坐标系. B A 1 1 则C(0,1,2),B(2,4,0), ∴BC =(－2,－3,2), 1 1 D C y CD=(0,－1,0),设BC 与CD所成的角为θ, 1 A B x BC CD 3 17 3 17 则cosθ= 1 = ,θ= arccos . 17 17 BC  CD 1 3 17 异面直线BC与DC所成角的大小为arccos 1 17 2 18. [解] 原方程化简为 z (z z)i 1i, 设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1－i, 1 3 ∴x2+y2=1且2x=－1,解得x=－ 且y=± , 2 2 1 3 ∴原方程的解是z=－ ± i. 2 2 19. [解]（1）由已知可得点A(－6,0),F(0,4) 设点P(x,y),则AP={x+6,y},FP={x－4,y}, x2 y2   1 由已知可得 36 20  (x6)(x4) y2 0 3 则2x2+9x－18=0,解得x= 或x=－6. 2 3 5 3 由于y>0,只能x= ,于是y= . 2 2 3 5 3 ∴点P的坐标是( , ) 2 2 (2) 直线AP的方程是x－ 3y+6=0. 第6页 | 共8页m6 设点M(m,0),则M到直线AP的距离是 . 2 m6 于是 = m6 ,又－6≤m≤6,解得m=2. 2 椭圆上的点(x,y)到点M的距离d有 5 4 9 d2=(x－2)2+y2=x－4x2+4+20－ x2= (x－ )2+15, 9 9 2 9 由于－6≤m≤6, ∴当x= 时,d取得最小值 15 2 20. [解](1)设中低价房面积形成数列{a},由题意可知{a}是等差数列, 其中a=250,d=50, n n 1 n(n1) 则S=250n+ 50=25n2+225n, n 2 令25n2+225n≥4750,即n2+9n-190≥0,而n是正整数, ∴n≥10. ∴到2013年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米. (2)设新建住房面积形成数列{b},由题意可知{b}是等比数列,其中b=400,q=1.08, n n 1 则b=400·(1.08)n-1. n 由题意可知a>0.85 b,有250+(n-1)·50>400·(1.08)n-1·0.85. n n 由计算器解得满足上述不等式的最小正整数n=6. ∴到2009年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.  x2  x(,1)  (1,) 21. [解] (1)h(x)x1  1 x1 x2 1 (2) 当x≠1时, h(x)= =x－1+ +2, x1 x1 若x>1时, 则h(x)≥4,其中等号当x=2时成立 若x<1时, 则h(x)≤ 0,其中等号当x=0时成立 ∴函数h(x)的值域是(－∞,0]∪{1}∪[4,+∞)  (3)令 f(x)=sin2x+cos2x,α= 4   则g(x)=f(x+α)= sin2(x+ )+cos2(x+ )=cos2x－sin2x, 4 4 于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x－sin2x)=cos4x.  另解令f(x)=1+ 2 sin2x, α= , 2 g(x)=f(x+α)= 1+ 2 sin2(x+π)=1－ 2 sin2x, 于是h(x)= f(x)·f(x+α)= (1+ 2 sin2x)( 1－ 2 sin2x)=cos4x. 22. [解](1)设点A(x,y), A为P关于点的对称点A的坐标为(2－x,4－y), 0 0 1 0 A为P关于点的对称点A的坐标为(2+x,4+y), 1 2 2 第7页 | 共8页∴A A ={2,4}. 0 2 (2) ∵A A ={2,4}, 0 2 ∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到. 因此, 曲线C是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,且当x∈(－2,1]时,g(x) =lg(x+2)－4.于是,当x∈(1,4]时,g(x)=lg(x－1)－4. 另解设点A(x,y), A(x,y),于是x－x=2,y－y=4, 0 2 2 2 2 2 若3< x≤6,则0< x－3≤3,于是f(x)=f(x－3)=lg(x－3). 2 2 2 2 2 当1< x≤4时, 则3< x≤6,y+4=lg(x－1). 2 ∴当x∈(1,4]时,g(x)=lg(x－1)－4. (3)A A =A A  A A   A A , 0 n 0 2 2 4  n2 n 由于A A  2P P ,得 2k2 2k 2k1 2k A A =2(PP P P  P P ) 0 n 1 2 3 4  n1 n n 2(2n 1) 4(2n 1) =2({1,2}+{1,23}+┄+{1,2n－1})=2{ , }={n, } 2 3 3 第8页 | 共8页