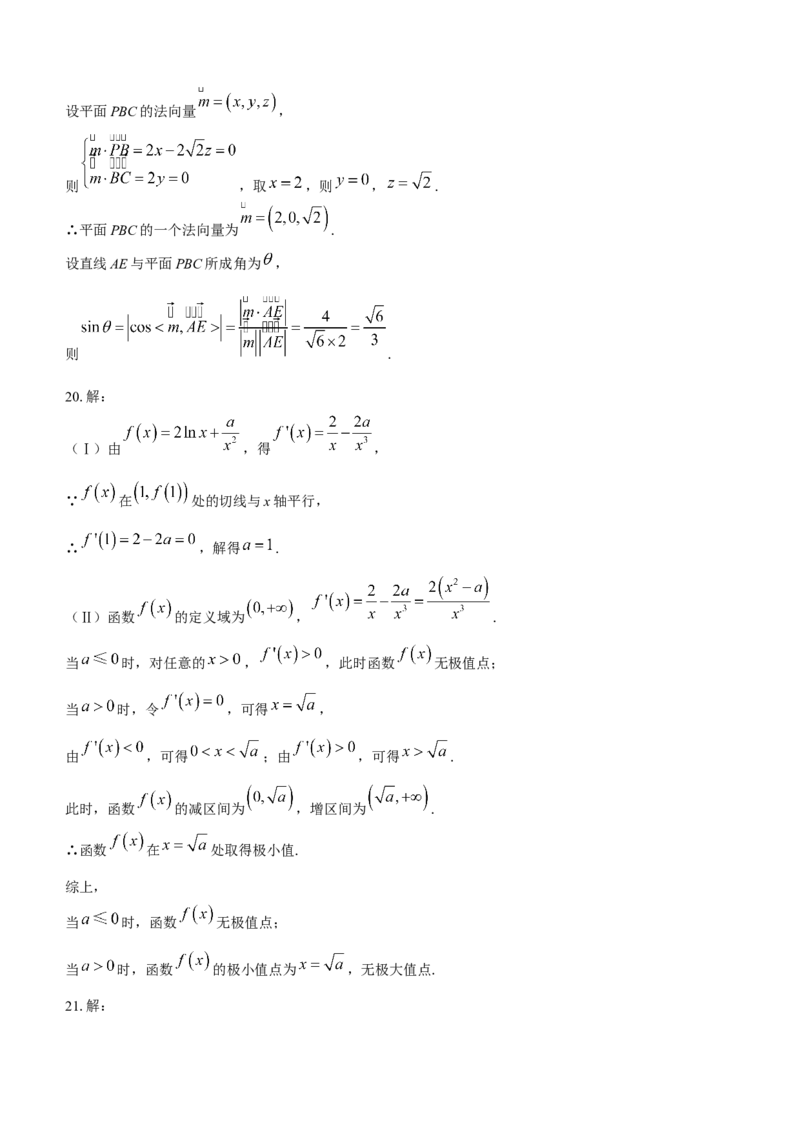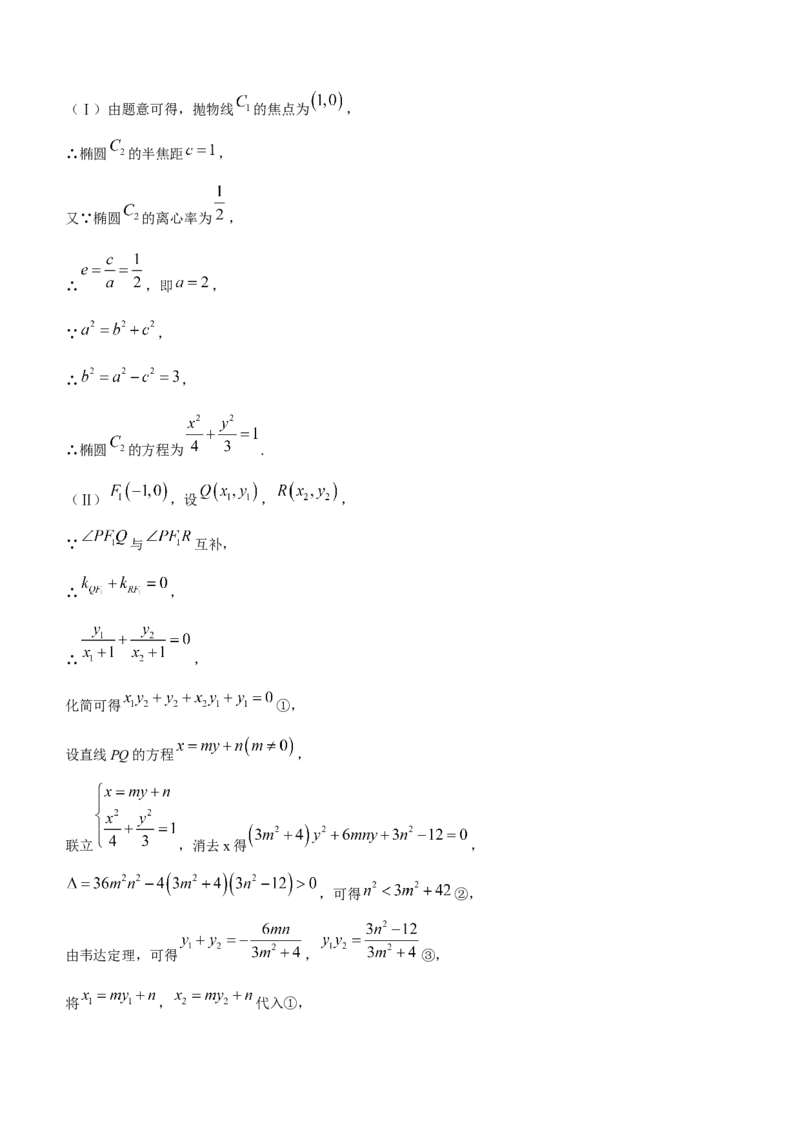文档内容
2024 届高三第三次校际联考
数学(理科)试题
注意事项:
1.本试题共4页,满分150分,时间120分钟.
2.答卷前,务必将答题卡上密封线内的各项目填写清楚.
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试
卷上无效.
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题不回收.
第Ⅰ卷(选择题 共 60 分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知复数z满足 ,则z的虚部为
A. B. C. D.
2.命题“ , ”的否定是
A. , B. ,
C. , D. ,
3.已知全集 ,集合 , ,则
A. B. C. D.
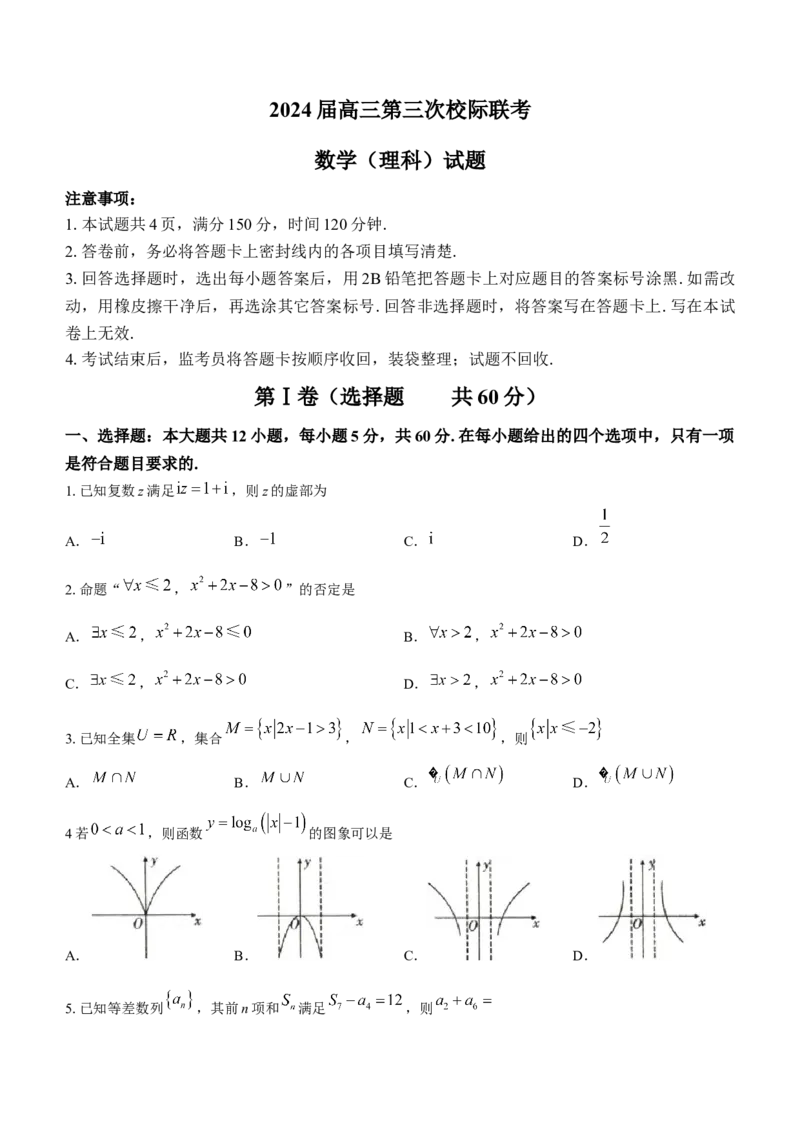
4若 ,则函数 的图象可以是
A. B. C. D.
5.已知等差数列 ,其前n项和 满足 ,则
学科网(北京)股份有限公司A.4 B. C. D.3
6.若圆 : 与圆 : 有且仅有3条公切线,则
A.14 B.28 C.9 D.
7.已知等比数列 为递减数列,若 , ,则
A. B. C. D.6
8.酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量达
到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血
液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那
么他至少经过几个小时才能驾驶?(参考数据: , , )
A.3 B.4 C.5 D.6
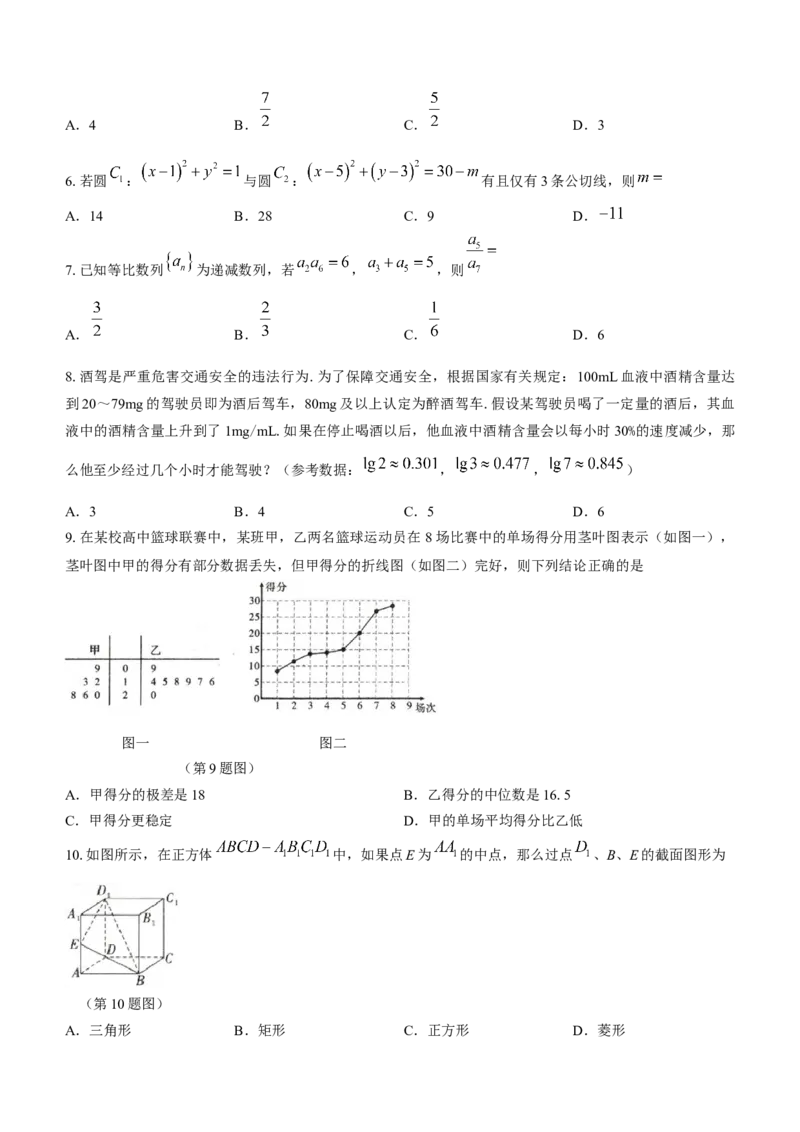
9.在某校高中篮球联赛中,某班甲,乙两名篮球运动员在 8场比赛中的单场得分用茎叶图表示(如图一),
茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(如图二)完好,则下列结论正确的是
图一 图二
(第9题图)
A.甲得分的极差是18 B.乙得分的中位数是16.5
C.甲得分更稳定 D.甲的单场平均得分比乙低
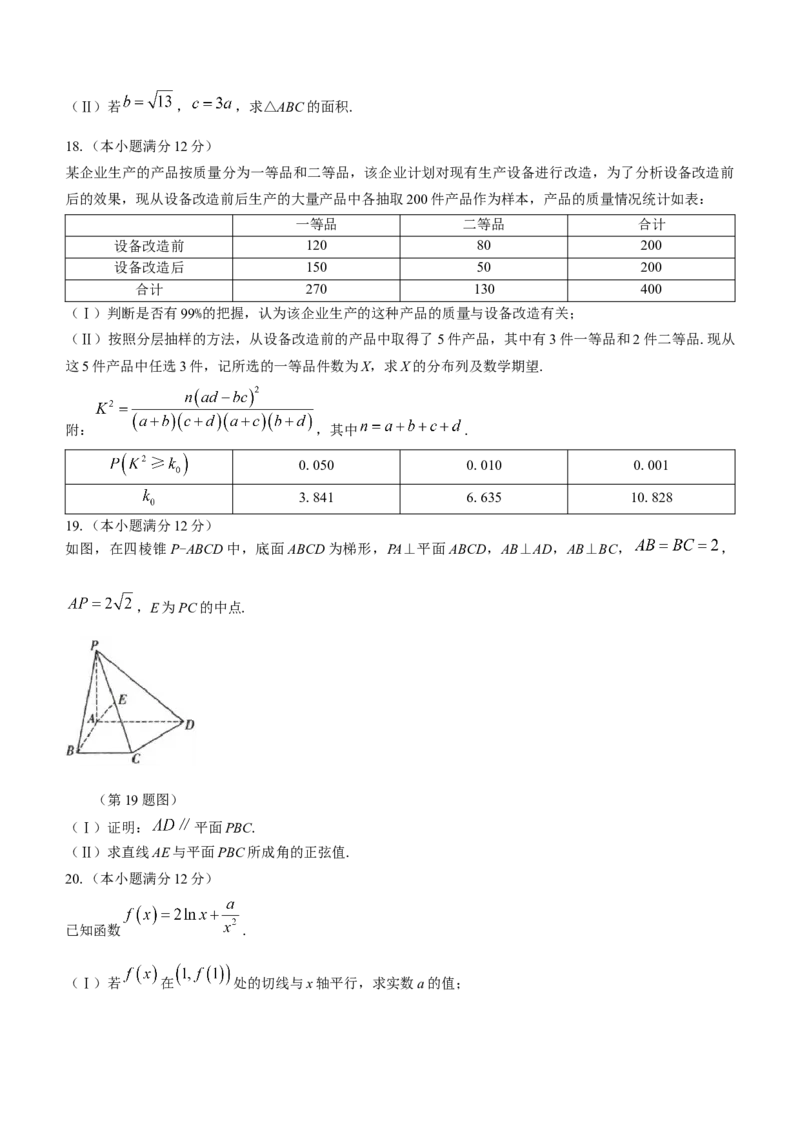
10.如图所示,在正方体 中,如果点E为 的中点,那么过点 、B、E的截面图形为
(第10题图)
A.三角形 B.矩形 C.正方形 D.菱形
学科网(北京)股份有限公司11.设P是双曲线 ( , )与圆 在第一象限的交点, 、 分别是
双曲线的左、右焦点,若 ,则双曲线的离心率为
A. B. C. D.
12.已知实数a,b,c满足 ,则a,b,c的大小关系为
A. B. C. D.
第Ⅱ卷(非选择题 共 90 分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知抛物线 的焦点为F,点P在该抛物线上,且P的横坐标为4,则 .
14.在△ABC中, , ,则 .
15.根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.算筹计数法就是用一根根同
样长短和粗细的小棍子以不同的排列方式来表示数字,如图所示.如果用算筹随机摆出一个不含数字0的两位
数,个位用纵式,十位用横式,则个位和十位上的算筹不一样多的概率为 .
纵式:
横式:
(第15题图)
16.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为 ,两个圆锥的高之比为
1∶3,则这两个圆锥的侧面积之和为 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每
个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)
已知△ABC的内角A,B,C的对边分别为a,b,c,且 .
(Ⅰ)求角B;
学科网(北京)股份有限公司(Ⅱ)若 , ,求△ABC的面积.
18.(本小题满分12分)
某企业生产的产品按质量分为一等品和二等品,该企业计划对现有生产设备进行改造,为了分析设备改造前
后的效果,现从设备改造前后生产的大量产品中各抽取200件产品作为样本,产品的质量情况统计如表:
一等品 二等品 合计
设备改造前 120 80 200
设备改造后 150 50 200
合计 270 130 400
(Ⅰ)判断是否有99%的把握,认为该企业生产的这种产品的质量与设备改造有关;
(Ⅱ)按照分层抽样的方法,从设备改造前的产品中取得了5件产品,其中有3件一等品和2件二等品.现从
这5件产品中任选3件,记所选的一等品件数为X,求X的分布列及数学期望.
附: ,其中 .
0.050 0.010 0.001
3.841 6.635 10.828
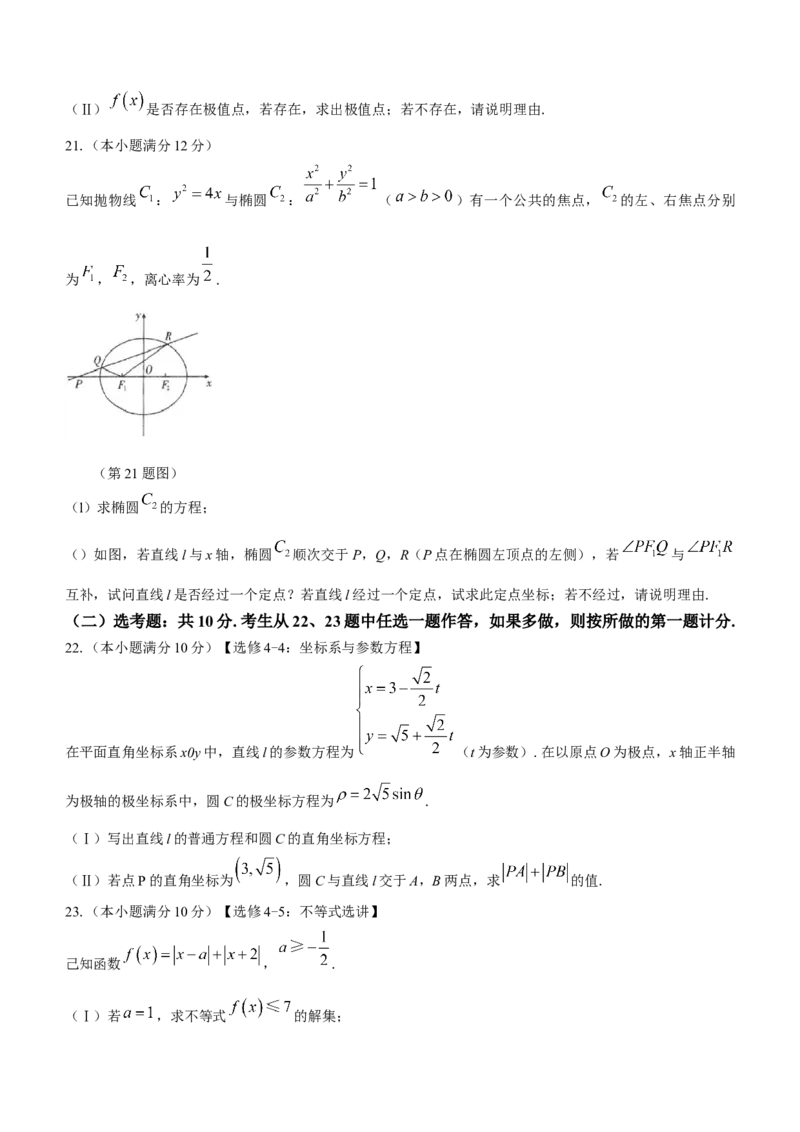
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD为梯形,PA⊥平面ABCD,AB⊥AD,AB⊥BC, ,
,E为PC的中点.
(第19题图)
(Ⅰ)证明: 平面PBC.
(Ⅱ)求直线AE与平面PBC所成角的正弦值.
20.(本小题满分12分)
已知函数 .
(Ⅰ)若 在 处的切线与x轴平行,求实数a的值;
学科网(北京)股份有限公司(Ⅱ) 是否存在极值点,若存在,求出极值点;若不存在,请说明理由.
21.(本小题满分12分)
已知抛物线 : 与椭圆 : ( )有一个公共的焦点, 的左、右焦点分别
为 , ,离心率为 .
(第21题图)
(l)求椭圆 的方程;
()如图,若直线l与x轴,椭圆 顺次交于P,Q,R(P点在椭圆左顶点的左侧),若 与
互补,试问直线l是否经过一个定点?若直线l经过一个定点,试求此定点坐标;若不经过,请说明理由.
(二)选考题:共10分.考生从22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)【选修4-4:坐标系与参数方程】
在平面直角坐标系x0y中,直线l的参数方程为 (t为参数).在以原点O为极点,x轴正半轴
为极轴的极坐标系中,圆C的极坐标方程为 .
(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)若点P的直角坐标为 ,圆C与直线l交于A,B两点,求 的值.
23.(本小题满分10分)【选修4-5:不等式选讲】
己知函数 , .
(Ⅰ)若 ,求不等式 的解集;
学科网(北京)股份有限公司(Ⅱ)若 ,求a的取值范围.
2024 届高三第三次校际联考
数学(理科)试题参考答案及评分标准
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.B 2.A 3.D 4.D 5.A 6.A 7.A 8.C 9.B 10.D 11.D 12.C
二、填空题:本大题共4小题,每小题5分,共20分.
13.5 14. 15. 16.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每
个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.解:
(Ⅰ)∵ ,
∴由正弦定理可得 ,
又 ,∴ ,即 ,
∵ ,
∴ .
(Ⅱ)∵ , , ,
∴由余弦定理可得 ,即 ,
解得 ,即 , ,
∴ .
18.解:
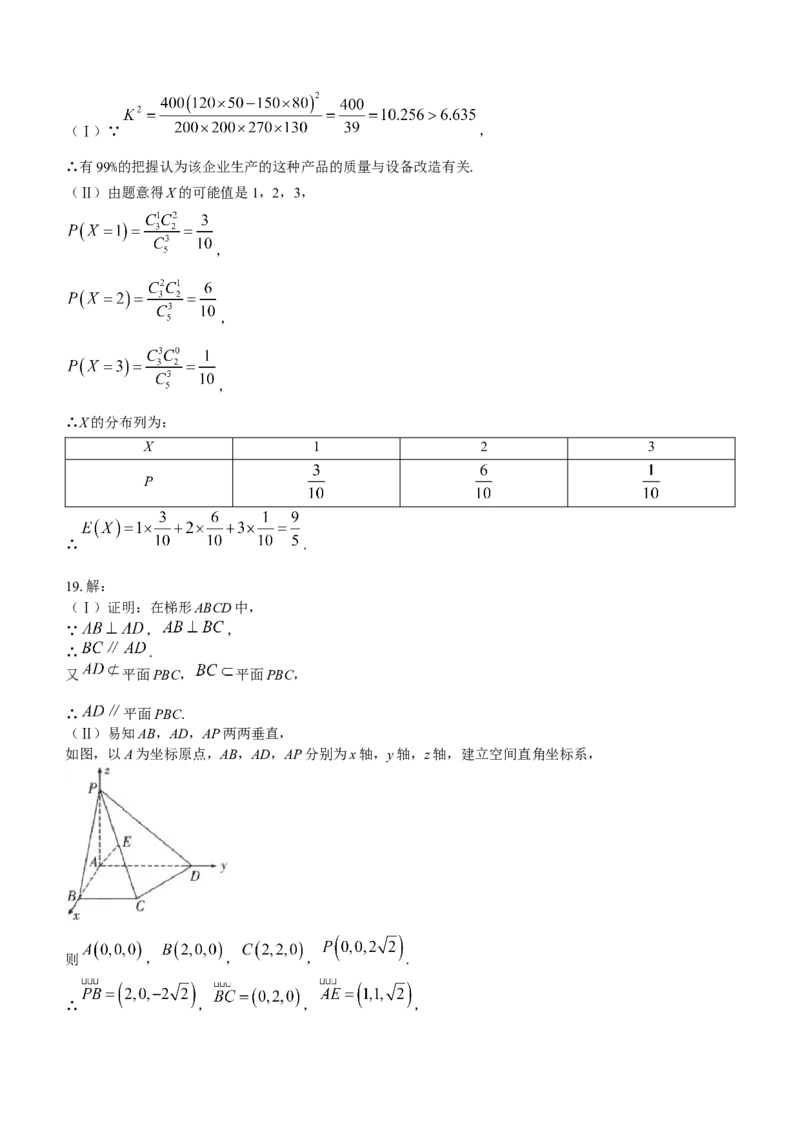
学科网(北京)股份有限公司(Ⅰ)∵ ,
∴有99%的把握认为该企业生产的这种产品的质量与设备改造有关.
(Ⅱ)由题意得X的可能值是1,2,3,
,
,
,
∴X的分布列为:
X 1 2 3
P
∴ .
19.解:
(Ⅰ)证明:在梯形ABCD中,
∵ , ,
∴ .
又 平面PBC, 平面PBC,
∴ 平面PBC.
(Ⅱ)易知AB,AD,AP两两垂直,
如图,以A为坐标原点,AB,AD,AP分别为x轴,y轴,z轴,建立空间直角坐标系,
则 , , , .
∴ , , ,
学科网(北京)股份有限公司设平面PBC的法向量 ,
则 ,取 ,则 , .
∴平面PBC的一个法向量为 .
设直线AE与平面PBC所成角为 ,
则 .
20.解:
(Ⅰ)由 ,得 ,
∵ 在 处的切线与x轴平行,
∴ ,解得 .
(Ⅱ)函数 的定义域为 , .
当 时,对任意的 , ,此时函数 无极值点;
当 时,令 ,可得 ,
由 ,可得 ;由 ,可得 .
此时,函数 的减区间为 ,增区间为 .
∴函数 在 处取得极小值.
综上,
当 时,函数 无极值点;
当 时,函数 的极小值点为 ,无极大值点.
21.解:
学科网(北京)股份有限公司(Ⅰ)由题意可得,抛物线 的焦点为 ,
∴椭圆 的半焦距 ,
又∵椭圆 的离心率为 ,
∴ ,即 ,
∵ ,
∴ ,
∴椭圆 的方程为 .
(Ⅱ) ,设 , ,
∵ 与 互补,
∴ ,
∴ ,
化简可得 ①,
设直线PQ的方程 ,
联立 ,消去x得 ,
,可得 ②,
由韦达定理,可得 , ③,
将 , 代入①,
学科网(北京)股份有限公司可得 ④,
再将③代入④,可得 ,解得 ,
∴直线PQ的方程为 ,
∴直线l经过定点 .
(二)选考题:共10分.考生从22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.解:
(Ⅰ)由直线l的参数为 (t为参数),
得直线l的普通方程为 .
将圆C的极坐标方程: 两边同乘 得 ,
化为直角坐标方程为 .
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得 ,即 ,
设 , 是A和B对应的参数,
则 , ,
又直线l过点 ,
∴ .
23.解:
(Ⅰ)当 时, ,
当 时,不等式 化为 ,
∴ ,此时 ;
学科网(北京)股份有限公司当 时,不等式 化为 ,恒成立,此时 ;
当 时,不等式 化为 ,
∴ ,此时 .
综上所述,不等式 的解集为 .
(Ⅱ) ,
若 ,则 ,
不等式两边平方可得 ,解得 ,
又 ,
∴ ,
即a的取值范围是 .
学科网(北京)股份有限公司