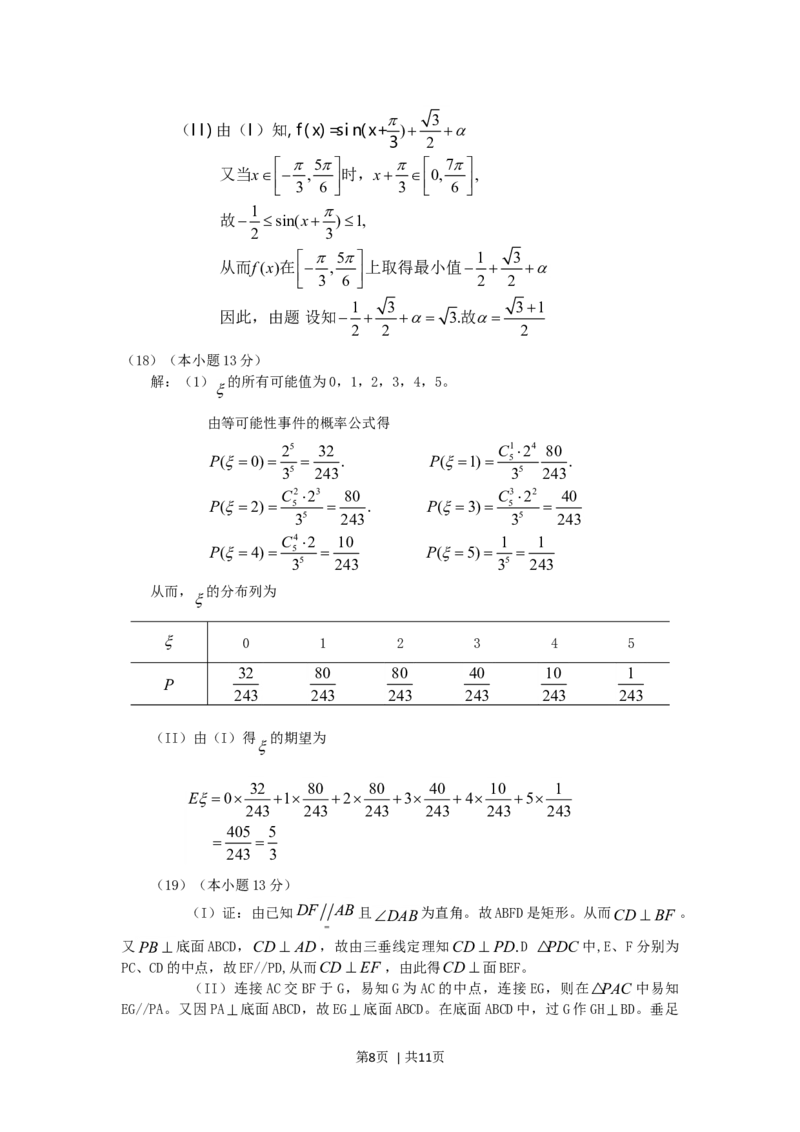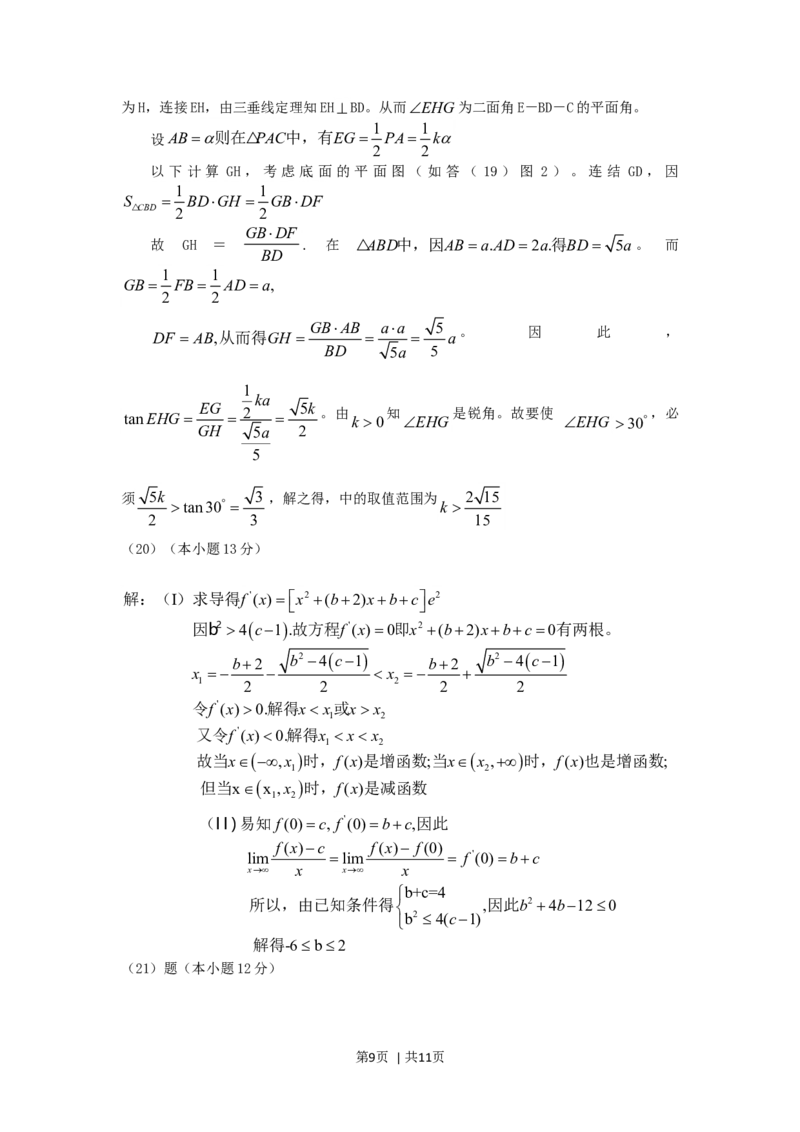2006年重庆高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_重庆

2006 年重庆高考理科数学真题及答案 一、选择题：本大题共10小题，每小题5分。在每小题给出的四个备选项中，只有一项是 符合题目要求的。 （ 1 ） 已 知 集 合 U   1,2,3,4,5,6,7  ,A  2,4,5,7  ,B   3,4,5 ， 则  痧A( B) ＝ U U （ ） （A） 1,6  （B） 4,5  （C） 2,3,4,5,7  （D）{ 1,2,3,6,7 } （2）在等差数列 中，若 ， 是数列的 的前n项和，则 的值为（ a a a 12 S a S n 4 6 n n 9 ） （A）48 (B)54 (C)60 （D）66 5 （3）过坐标原点且与圆x2  y2 4x2y 0相切的直线方程为（ ） 2 1 1 （A）y  3x或y  x （B）y 3x或y   x 3 3 1 1 （C）y  3x或y   x （D）y 3x或y  x 3 3 （4）对于任意的直线l与平面，在平面内必有直线m，使m与l（ ） （A）平行 （B）相交 （C）垂直 （D）互为异面直线 n  1  （5）若 的展开式中各项系数之和为64，则展开式的常数项为（ ） 3 x      x  （A）－540 （B）－162 （C）162 （D）540 （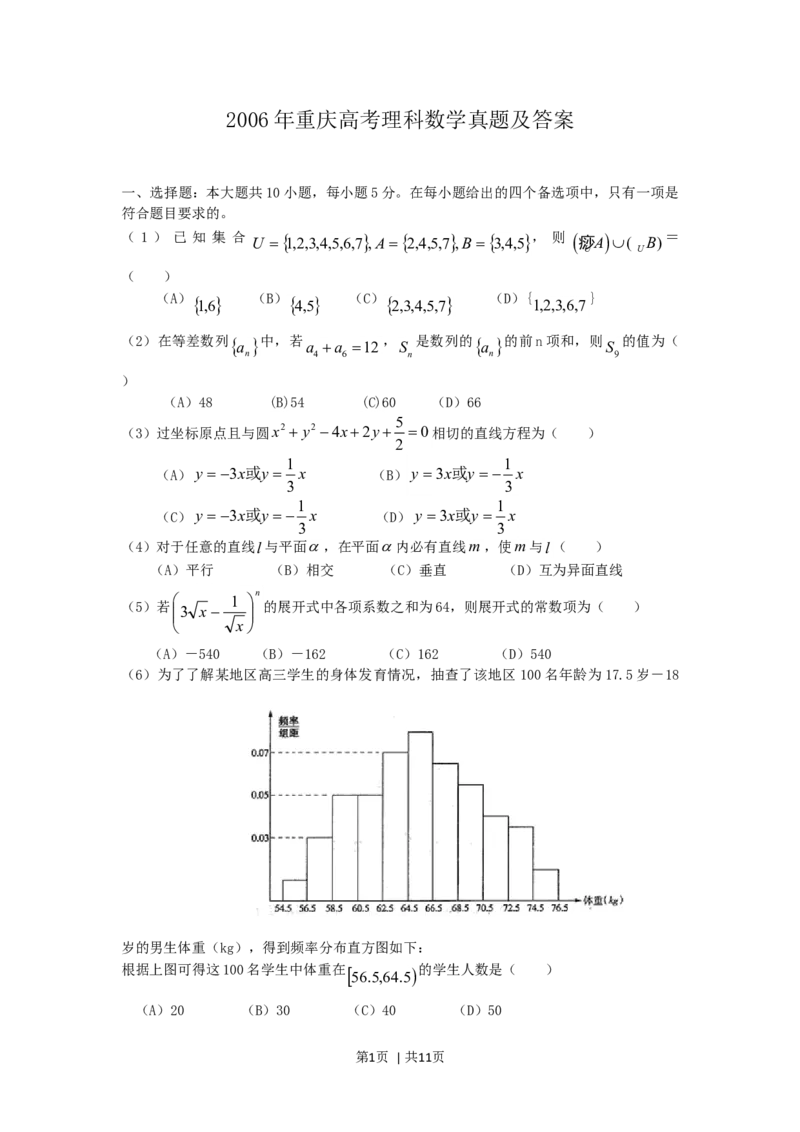6）为了了解某地区高三学生的身体发育情况，抽查了该地区 100名年龄为17.5岁－18 岁的男生体重（kg），得到频率分布直方图如下： 根据上图可得这100名学生中体重在 的学生人数是（ ） 56.5,64.5 （A）20 （B）30 （C）40 （D）50 第1页 | 共11页（7）与向量  7 1 1 7的夹角相等，且模为1的向量是（ ） a , ,b ,     2 2 2 2 4 3 4 3  4 3 2 2 1 （ A ）  , （ B ）  , 或 , （ C ）  , （ D ）   5 5 5 5  5 5  3 3  2 2 1  2 2 1  , 或 ,      3 3 3 3     （8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的 分配方案有（ ） （A）30种 （B）90种 （C）180种 （D）270种 （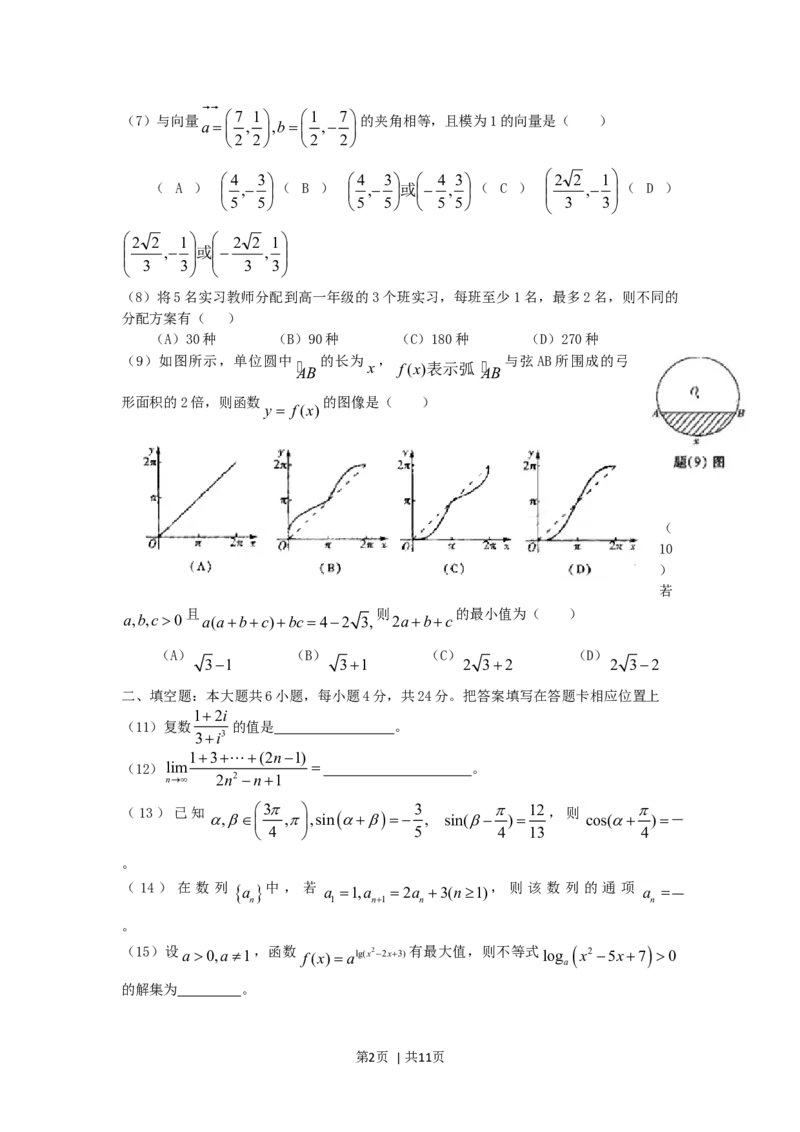9）如图所示，单位圆中 的长为 ， 与弦AB所围成的弓 AB x f(x)表示弧 AB 形面积的2倍，则函数 的图像是（ ） y  f(x) （ 10 ） 若 且 则 的最小值为（ ） a,b,c0 a(abc)bc42 3, 2abc （A） （B） （C） （D） 31 31 2 32 2 32 二、填空题：本大题共6小题，每小题4分，共24分。把答案填写在答题卡相应位置上 12i （11）复数 的值是 。 3i3 13(2n1) （12）lim  。 n 2n2 n1 （13）已知 ,   3 ,   ,sin 3 , sin(  ) 12，则 cos(  )  4  5 4 13 4 。 （ 14 ） 在 数 列 a 中 ， 若 a 1,a 2a 3(n1) ， 则 该 数 列 的 通 项 a  n 1 n1 n n 。 （15）设a 0,a 1，函数 f(x)alg(x22x3) 有最大值，则不等式log  x2 5x7  0 a 的解集为 。 第2页 | 共11页（16）已知变量 满足约束条件 若目标函数 （其 x,y 1 x y4,2 x y2. z ax y 中 a0 ）仅在点3,1处取得最大值，则 a 的取值范围为 。 三、解答题：三大题共6小题，共76分。解答应写出文字说明、证明过程或演算步骤。 （17）（本小题满分13分） 设函数 （其中 ），且 的图 f(x) 3cos2xsinxcosx 0,R f(x)  y 象在 轴右侧的第一个最高点的横坐标为 。 6 （I）求的值。 （II）如果 在区间  5上的最小值为 ，求 的值。 f(x)   ,  3   3 6  （18）（本小题满分13分） 某大夏的一部电梯从底层出发后只能在第 18、19、20层可以停靠。若该电梯在底层 1 载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为 ，用表示这5位乘客 3 在第20层下电梯的人数，求： （I）随机变量 的分布列;  （II）随机变量 的期望;  （19）（本小题满分13分） 如图，在四棱锥 PABCD中，PA底面ABCD，DAB为 直角， , E、F分别为 、 中点。 AB//CD ADCD2AB, PC CD （I）试证：CD平面BEF ; （II）高 PAkAB，且二面角 EBDC的平面角大小 ，求 的取值范围。 30 k （20）（本小题满分13分） 已知函数 f(x)  x2 bxc  e2，其中b,cR为常数。 （I）若 ，讨论函数 的单调性； b2 4c1 f(x) f(x)c （II）若b2 4(c1)，且lim 4，试证：6b2 x x （21）（本小题满分12分） 第3页 | 共11页已知定义域为R的函数 f(x)满足 f  f(x)x2 x   f(x)x2 x. 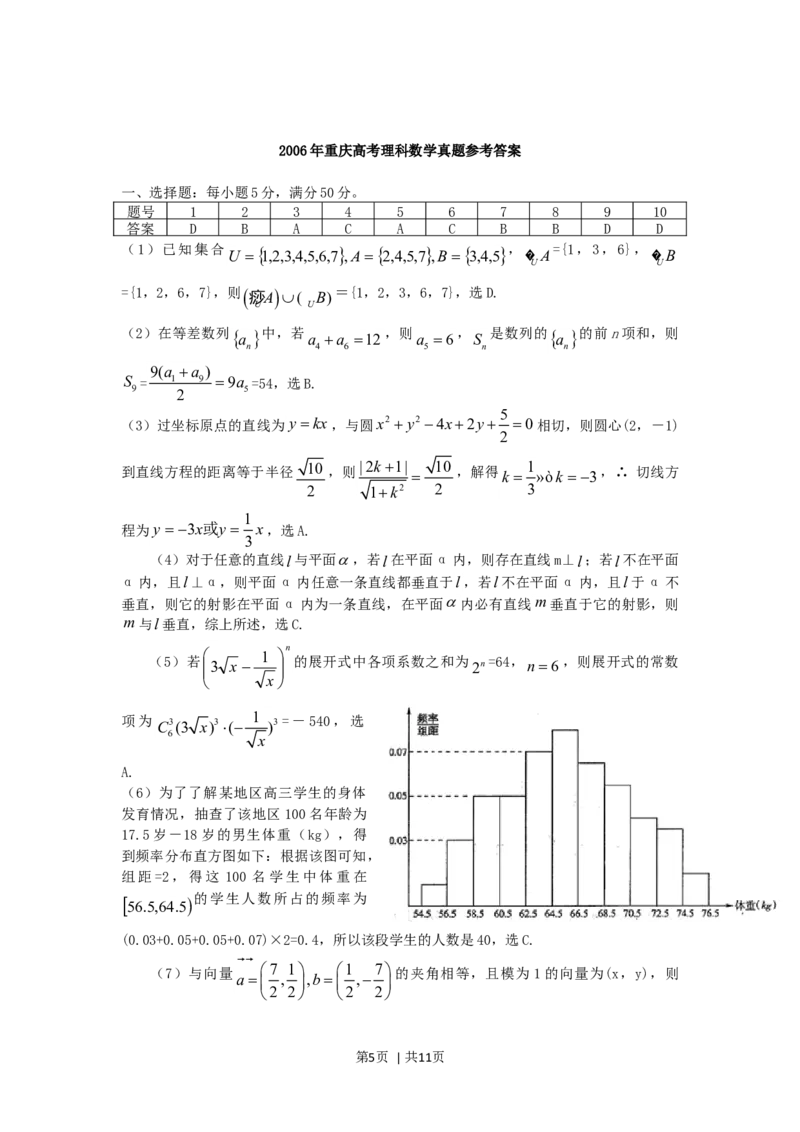（I）若 ，求 ;又若 ，求 ; f(2)3 f(1) f(0)a f(a) （II）设有且仅有一个实数 ，使得 ，求函数 的解析表达式 x f(x ) x f(x) 0 0 0 （22）（本小题满分12分） 已知一列椭圆 y2 。 ……。 c :x2  1,0b 1 n1,2 n b2 n n 若椭圆 C 上有一点 P ，使 P 到右准线 l 的距离 d 是p F 与 n n n n n n n PG 的等差中项，其中 F 、 G 分别是 C 的左、右焦点。 n n n n n （I）试证： b  3 n1; n 2 （II）取 2n3 ，并用 表示 的面积， b  S PFG n n2 n n n n 试证： S S 且 S S n3 1 2 n n1 第4页 | 共11页2006年重庆高考理科数学真题参考答案 一、选择题：每小题5分，满分50分。 题号 1 2 3 4 5 6 7 8 9 10 答案 D B A C A C B B D D （1）已知集合 U   1,2,3,4,5,6,7  ,A  2,4,5,7  ,B   3,4,5 ， � A ={1，3，6}， � B U U ={1，2，6，7}，则 痧A( B) ＝{1，2，3，6，7}，选D. U U （2）在等差数列 中，若 ，则 ， 是数列的 的前n项和，则 a a a 12 a 6 S a n 4 6 5 n n 9(a a ) S = 1 9 9a =54，选B. 9 2 5 5 （3）过坐标原点的直线为 y kx，与圆x2  y2 4x2y 0相切，则圆心(2，－1) 2 到直线方程的距离等于半径 10 ，则 |2k1| 10 ，解得 1 ，∴ 切线方  k  »òk 3 2 1k2 2 3 1 程为y  3x或y  x，选A. 3 （4）对于任意的直线l与平面，若l在平面α内，则存在直线m⊥l；若l不在平面 α内，且l⊥α，则平面α内任意一条直线都垂直于l，若l不在平面α内，且l于α不 垂直，则它的射影在平面α内为一条直线，在平面内必有直线m垂直于它的射影，则 m与l垂直，综上所述，选C. n  1  （5）若 的展开式中各项系数之和为 =64， ，则展开式的常数 3 x   2n n6    x  1 项为 =－540，选 C3(3 x)3( )3 6 x A. （6）为了了解某地区高三学生的身体 发育情况，抽查了该地区100名年龄为 17.5岁－18岁的男生体重（kg），得 到频率分布直方图如下：根据该图可知， 组距=2，得这 100 名学生中体重在  的学生人数所占的频率为 56.5,64.5 (0.03+0.05+0.05+0.07)×2=0.4，所以该段学生的人数是40，选C. （7）与向量  7 1 1 7的夹角相等，且模为 1的向量为(x，y)，则 a , ,b ,     2 2 2 2 第5页 | 共11页 4  4  x2  y2 1 x x    ，解得 5 或 5，选B. 7 1 1 7   x y  x y 3 3    y  y  2 2 2 2  5  5 （8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则将 C1C2 5名教师分成三组，一组1人，另两组都是2人，有 5 4 15 种方法，再将3组分到3 A2 2 个班，共有 种不同的分配方案，选B. 15A3 90 3 （9）如图所示，单位圆中 的长为 ， 与弦AB所围成的弓形面积的 AB x f(x)表示弧 AB 2倍，当 的长小于半圆时，函数 的值增加的越来越快，当 的长大于半圆 AB y  f(x) AB 时，函数 的值增加的越来越慢，所以函数 的图像是D. y  f(x) y  f(x) （10）若 且 所以 ， a,b,c0 a(abc)bc42 3, a2 abacbc42 3 1 1 42 3 a2 abacbc (4a2 4ab4ac2bc2bc)≤ (4a24ab4ac2bcb2c2) 4 4 ∴ ，则( )≥ ，选D. (2 32)2≤(2abc)2 2abc 2 32 二、填空题：每小题4分，满分24分。 1 7 1 56 （11）  i （12） （13） （14）2n13 10 10 2 65 （15）2,3 （16） a1 12i 12i (12i)(3i) 17i （11）复数 =   。 3i3 3i 10 10 （12） 13(2n1) n2 1 。 lim  lim  n 2n2 n1 n2n2 n1 2 （13）已知 ,   3 ,   ,sin 3 , sin(  ) 12， ( 3 ,2) ，  4  5 4 13 2   3 4  5  ( , )，∴ cos() ，cos( ) ， 4 2 4 5 4 13   则 cos( ) cos[()( )]= 4 4   cos()cos( )sin()sin( ) 4 4 第6页 | 共11页4 5 3 12 56 = ( )( )  5 13 5 13 65 （14）在数列a 中，若 a 1,a 2a 3(n1) ，∴ a 32(a 3)(n1) ，即 n 1 n1 n n1 n { }是以 为首项，2为公比的等比数列， ，所以该数 a 3 a 34 a 342n1 2n1 n 1 n 列的通项 . a  2n13 n （15）设 a 0,a 1 ，函数 f(x)alg(x22x3) 有最大值，∵ lg(x2 2x3)≥lg2 有最小 值 ， ∴ 0