文档内容
2024-2025 学年浙江省浙东北县域名校发展联盟高二下学期期中考试
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列函数中既是偶函数,又在区间(0,+∞)上单调递增的是( )
1
A. y=x B. y=− C. y=−|x| D. y=x2
x
2.已知随机变量X~N(2,σ2), 且P(X<0)=0.2, 则P(X> 4)=( )
A. 0.6 B. 0.4 C. 0.2 D. 0.1
3.下列函数求导正确的是( )
2 1 1
A. (2lnx)′= B. (sinx)′=−cosx C. (e2x )′=2ex D. ( )′=
x x x2
4.已知函数 {10x,x<10, 则 ( )
f(x)= f [f(100)]=
lgx,x⩾10,
A. 1010 B. 100 C. 2 D. 1
5.某活动共包含A、B、C、D、E这5个环节,其中环节A、B必须相邻,环节C、D不能相邻,那么不同
的安排方式一共有( )
A. 12种 B. 24种 C. 36种 D. 48种
1 1 1
6.对于随机事件A、B,若P(A)= ,P(A|B)= ,P(B|A)= ,则P(B)=( )
2 3 4
1 2 3 3
A. B. C. D.
2 3 4 8
7.已知随机变量 , 呈现非线性关系 为了进行线性回归分析,设 , ,
x y(x>0,y>0) . u=3ln y v=(4x−5) 2
1
利用最小二乘法,得到线性回归方程u=− v+3,则变量y的估计值有( )
4
A. 最大值为e B. 最小值为e C. 最大值为e3 D. 最小值为e3
8.已知函数f(x),g(x)的定义域为R,f(−x+1)+g(x+1)=f(x+2)−g(x)=1,且f(x)满足
2025
, ,则 ( )
f ′(x+1)+f ′(−x+1)=0 g(1)=−1 ∑ f(k)=
k=1
第 页,共 页
1 1A. −1 B. 1 C. 2025 D. 2026
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列结论正确的是( )
A. 将一组数据中的每一个数据都加上或减去同一个常数后,方差不变
B. 在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
C. 两个具有线性相关关系的变量的相关性越强,则线性相关系数r的绝对值越接近于0
n ̂(cid:27)
∑(y −y ) 2
i i
D. 决定系数 R2=1− i=1 可以衡量一个模型拟合效果,它越大说明拟合效果越好
n
∑(y −y) 2
i
i=1
10.已知函数 x2+2x−2,则下列结论正确的有( )
f(x)=
ex
A. f(x)共有3个零点
B. f(x)既存在极大值,也存在极小值
6
C. 若x∈[t,+∞)时,f(x) = ,则t的最大值为2
max e2
6
D.
若函数y=f(x)−k有2个零点,则k∈(−2e2,0]∪{
}
e2
11.高考数学新课标Ⅰ卷试题的第二部分为多选题,每题设有4个选项,其中正确选项的数量为2个或3个.若
正确答案共2个选项,每选对1个得3分;若正确答案共3个选项,每选对1个得2分.需要注意的是,全部选对
才能得6分,一旦选中任何错误选项,该题即得0分.张三对其中的某题完全不会,若该题共有三个正确选
2
项的概率是 ,记X、Y、Z分别为张三随机选择1个、2个、3个选项的得分,则( )
3
1
A. P(X=2)= B. P(Y =4)=P(X=3)+P(Z=6)
2
C. E(Z)D(Y)>D(X)
三、填空题:本题共3小题,每小题5分,共15分。
12.设 ,则 .
(2x+1) 4=a +a x+a x2+a x3+a x4 a +a +a +a +a =
0 1 2 3 4 0 1 2 3 4
第 页,共 页
2 113.已知具有线性相关关系的变量x,y,设其样本点为A (x ,y )(i=1,2,3,⋯,8),经验回归方程为
i i i
8 8
̂(cid:27) ̂(cid:27) ,若 , ,则̂(cid:27) .
∑ x =40 ∑ y =−64
y=−2x+a
i i
a=
i=1 i=1
4
14.已知函数f(x)=|ax+ −b|(a,b∈R),当x∈[1,4]时,设f(x)的最大值为M(a,b),则M(a,b)
x
的最小值是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知函数 .
f(x)=x3−3x
(1)求函数f(x)的单调区间;
(2)求曲线y=f(x)在x=2处的切线方程.
16.(本小题15分)
2025年3月30日,第20届亚洲马拉松锦标赛在浙江嘉兴盛大启幕.为了解观众的观赛体验,从现场随机抽
取了200位观众开展相关调查,得到满意率为80%.
(1)根据所给数据,完成2×2列联表;
满意度
性别 合计
满意 不满意
男性 20
女性 40
合计
(2)在(1)的条件下,依据小概率值α=0.005的独立性检验,能否认为性别与满意度有关联?
附: n(ad−bc) 2 , .
χ2= n=a+b+c+d
(a+b)(c+d)(a+c)(b+d)
α 0.050 0.0100.005 0.001
x 3.841 6.6357.879 10.828
α
17.(本小题15分)
2
已知(x− ) n的展开式中共有7项.
x
(1)求n的值;
(2)求展开式中二项式系数最大的项;
2
(3)求(2+x2 )(x− ) n的展开式中含x2的项的系数.
x
第 页,共 页
3 118.(本小题17分)
近年来,购买盲盒成为当下年轻人的潮流之一.2025年初,中国动画电影《哪吒2》火爆上映,引发观影
3
热潮.随后,某手办店乘势推出一系列单价相同、款式各异的手办盲盒,其中开出哪吒手办的概率是 ,开
5
2
出敖丙手办的概率是 .
5
(1)若张三到该店购买3个盲盒,设其开出哪吒手办的个数为X,求X的分布列和期望;
(2)若张三到该店购买8个盲盒,求其开出的哪吒盲盒最有可能的数量;
(3)若该店开展活动,当顾客在购买手办盲盒过程中,连续开出2个哪吒手办时,可获赠1个齐天大圣手办.
已知手办盲盒单价为9元,那么平均花多少钱能获得1个齐天大圣手办?
19.(本小题17分)
已知函数f(x)=xlnx.
(1)求f(x)的最小值,并求出相应的x;
(2)若f(x)≥a(x−√x)对任意x∈(0,+∞)恒成立,求实数a的值;
1
(3)若直线y=m(其中− 0,得x<−1或x>1,
所以f(x)的单调递增区间为(−∞,−1),(1,+∞);
f(x)的单调递减区间为(−1,1).
(2)k=f ′(2)=9,
f(2)=2,所以切线方程为y−2=9(x−2),即y=9x−16.
16.解:(1)2×2列联表如下:
满意度
性别 合计
不满
满意
意
男性120 20 140
女性40 20 60
合计160 40 200
第 页,共 页
5 1(2)零假设H :性别与满意度无关联,
0
200(120×20−20×40) 2
此时χ2= ≈9.524>7.879,
160×40×60×140
根据小概率值α=0.005的独立性检验,推断H 不成立,
0
即认为性别与满意度有关联,此推断犯错误的概率不大于0.005.
17.解:(1)由n+1=7,解得n=6;
2
(2)由(1)知展开式的通项为T =Ckx6−k (− ) k=(−2) kCkx6−2k,
k+1 6 x 6
2
所以T =C3x3 (− ) 3=−160;
4 6 x
令 ,得 ,即
(3) 6−2k=2 k=2 T =(−2) 2C2x2=60x2;
3 6
令6−2k=0,由(2)知T =−160;
4
综上:展开式中x2的系数为60×2+(−160)×1=−40.
3
18.解:(1)X可取0,1,2,3,由题可知X∼B(3, ).
5
3 3
则P(X=k)=Ck ( ) k (1− ) 3−k.
3 5 5
3 3 8
则P(X=0)=C0 ( ) 0 (1− ) 3=
3 5 5 125
3 3 36
P(X=1)=C1 ( ) 1 (1− ) 2=
3 5 5 125
3 3 54
P(X=2)=C2 ( ) 2 (1− ) 1=
3 5 5 125
3 3 27
P(X=3)=C3 ( ) 3 (1− ) 0=
3 5 5 125
分布列:
X0 1 2 3
8 36 54 27
P
125 125 125 125
第 页,共 页
6 13 9
期望:E(X)=np=3× = ;
5 5
3
(2)设其开出的哪吒手办的数量为Y,则Y∼B(8, ).
5
3 3
所以P(Y =k)=Ck ( ) k (1− ) 8−k (k=0,1,2,⋯,8).
8 5 5
由{P(Y =k)⩾P(Y =k−1)
,
P(Y =k)⩾P(Y =k+1)
{ Ck(3) k (
1−
3) 8−k ⩾Ck−1(3) k−1 (
1−
3) 9−k
8 5 5 8 5 5
得 ,其中0≤k≤8且k∈Z.
Ck(3) k (
1−
3) 8−k ⩾Ck+1(3) k+1 (
1−
3) 7−k
8 5 5 8 5 5
8! 3 8! 3
{ × ⩾ ×(1− )
即 k!(8−k)! 5 (k−1)!(9−k)! 5 ,解得 .
4.4≤k≤5.4
8! 3 8! 3
×(1− )⩾ ×
k!(8−k)! 5 (k+1)!(7−k)! 5
又k∈Z,则k=5
所以开出的哪吒手办的最有可能的数量为5个.
(3)设通过活动购买第X个盲盒时,恰好连续开出2个哪吒手办,设其期望为E,
2 3 2 3 3 40
则E= (E+1)+ × (E+2)+ × ×2.解得E= .
5 5 5 5 5 9
40
故平均需花费9× =40元.
9
19. 解:(1)由f ′(x)=lnx+1(x>0).
1
令f ′(x)>0,得x> ,
e
第 页,共 页
7 11 1
所以f(x)在(0, )单调递减,在( ,+∞)单调递增.
e e
1 1 1
即当x= 时,f(x) =f( )=− .
e min e e
(2)由切线不等式lnx≤x−1(当且仅当x=1时等号成立),
1 1 1 1 1
可得ln ≤ −1,则lnx≥1− ,进一步ln√x≥1− ,化简得lnx≥2(1− ),
x x x √x √x
所以xlnx≥2(x−√x),即a=2.
验证充分性:
由题可知xlnx≥a(x−√x),即√xlnx−a(√x−1)≥0对任意x∈(0,+∞)恒成立.
当a=2时,可设g(x)=√xlnx−2√x+2,设t=√x>0,可得y=2tlnt−2t+2,y′=2lnt,
进而可得y=2tlnt−2t+2在(0,1]单调递减,在[1,+∞)单调递增,所以y = y| =0,
min t=1
所以g(x)≥0,
综上所述,可得a=2.
1 1
(3)设A(0,0),B(1,0),C( ,− ),
e e
1 1
由(1)、(2)知:当x∈(0, )时,lnx0,
e e
1
所以存在x ∈( ,1),使得ℎ′(x )=0,
0 e 0
1
所以函数ℎ(x)在( ,x )上单调递减,在(x ,1)上单调递增,
e 0 0
1
又ℎ( )= ℎ(1)=0,
e
1
所以当x∈( ,1)时,ℎ(x)<0,
e
第 页,共 页
8 11 1
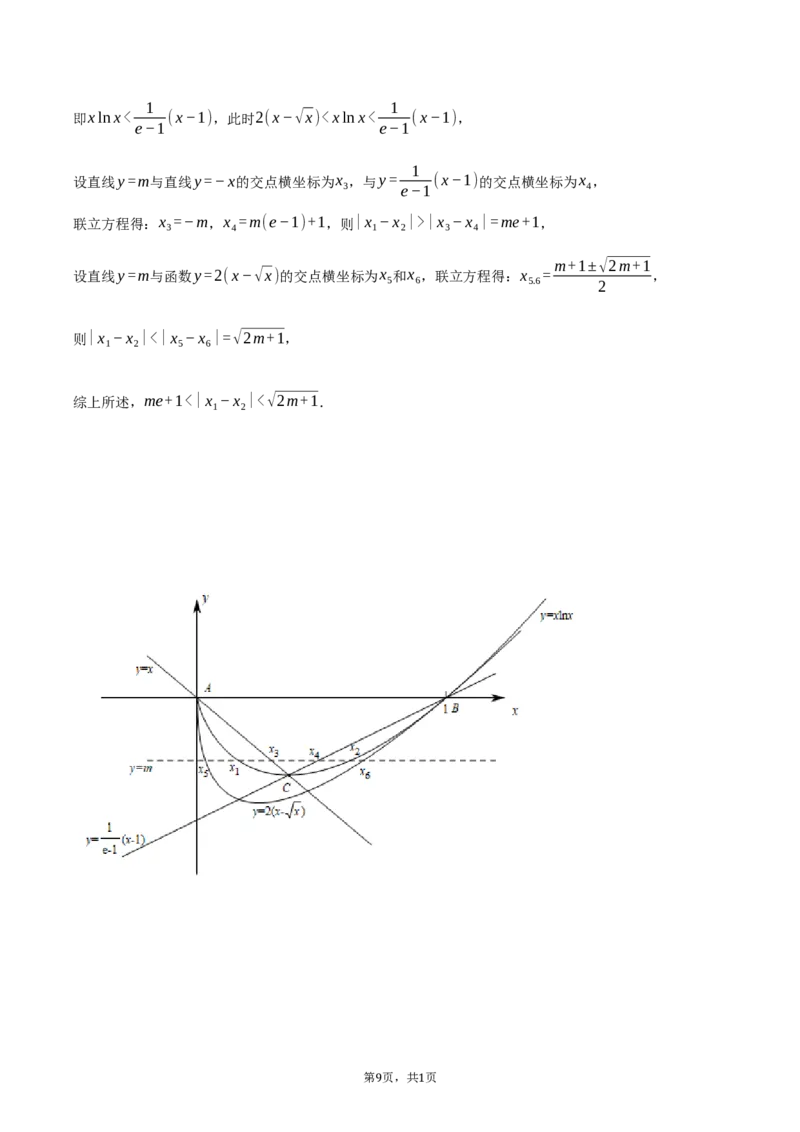
即xlnx< (x−1),此时2(x−√x)|x −x |=me+1,
3 4 1 2 3 4
m+1±√2m+1
设直线y=m与函数y=2(x−√x)的交点横坐标为x 和x ,联立方程得:x = ,
5 6 5.6 2
则|x −x |<|x −x |=√2m+1,
1 2 5 6
综上所述,me+1<|x −x |<√2m+1.
1 2
第 页,共 页
9 1