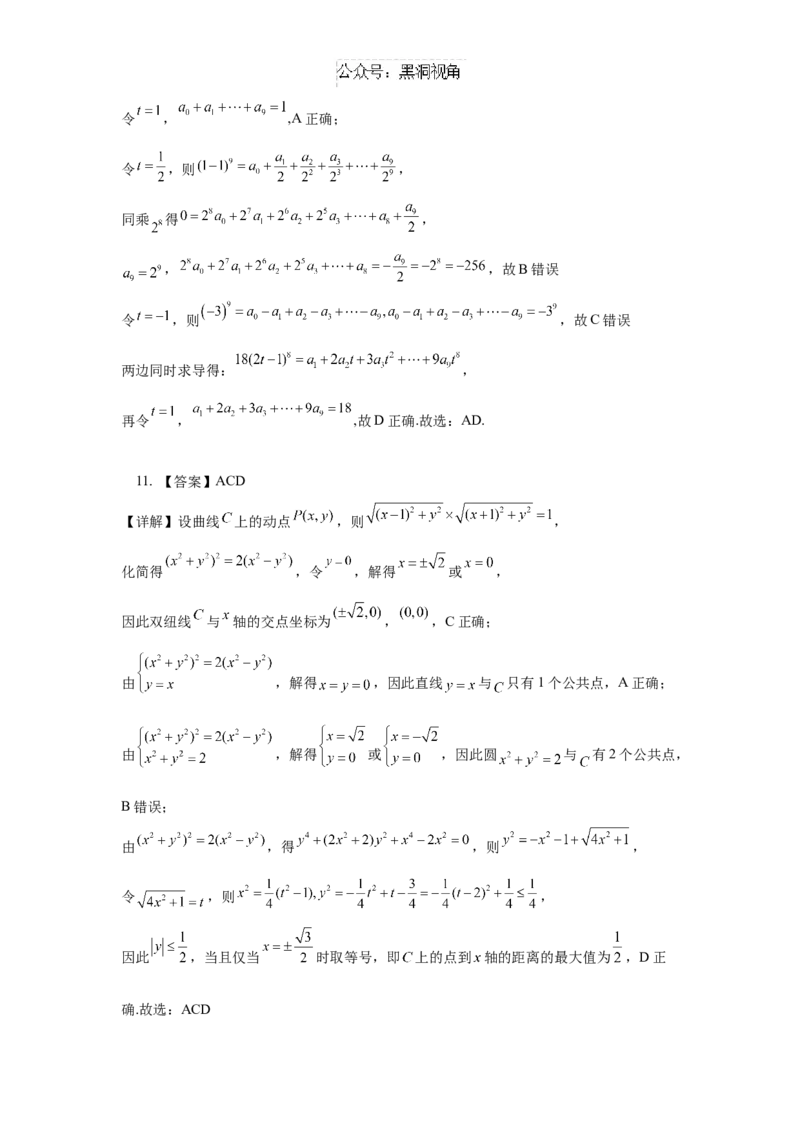文档内容
江苏省如皋中学 2024-2025 学年度第一学期综合练习(一)
数学试题
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.设集合 ,若 ,则 ( )
A. B. C. D.
2. 函数 的值域为( )
A. B. C. D.
3.3名同学分别报名参加足球队、篮球队、排球队、乒乓球队,每人限报一个运动队,不
同的报名方法种数有( )
A. B. C.24 D.12
4.有两箱零件,第一箱内有 件,其中有 件次品;第二箱内有 件,其中有 件次品.
现从两箱中随意挑选一箱,然后从该箱中随机取 个零件,则取出的零件是次品的概率
是( )
A. B. C. D.
5.已知点 是直线 上的动点,由点 向圆 引切线,切点分别为
且 ,若满足以上条件的点 有且只有一个,则 ( )
A. B. C.2 D.
6.如图所示,六氟化硫分子结构是六个氟原子处于顶点位置,而硫原子处于中心位置的正
八面体,也可将其六个顶点看作正方体各个面的中心点.若正八面体的表面积为 ,
则正八面体外接球的体积为( )
A.B.
C.
D.
7.已知数据 , , ,…, ,满足: ( ),若去掉 , 后组成
一组新数据,则新数据与原数据相比,下列说法错误的是( )
A.中位数不变 B.第35百分位数不变
C.平均数不变 D.方差不变
8. 已知定义在实数集 上的函数 ,其导函数为 ,且满足
, ,则 ( )
A. 0 B. C. 1 D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有
多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( ).
A.两个随机变量的线性相关性越强,样本相关系数就越接近于1
B.某校共有男女学生1500人,现按性别采用分层抽样的方法抽取容量为100人的样本,
若样本中男生有55人,则该校女生人数是675
C.对于独立性检验, 的观测值越大,推断“零假设 ”成立的把握越大
D.以 拟合一组数据时,经 代换后的线性回归方程为 ,则 ,
10. 已知 ,则下列结论成立的
是( )
A. B.C. D.
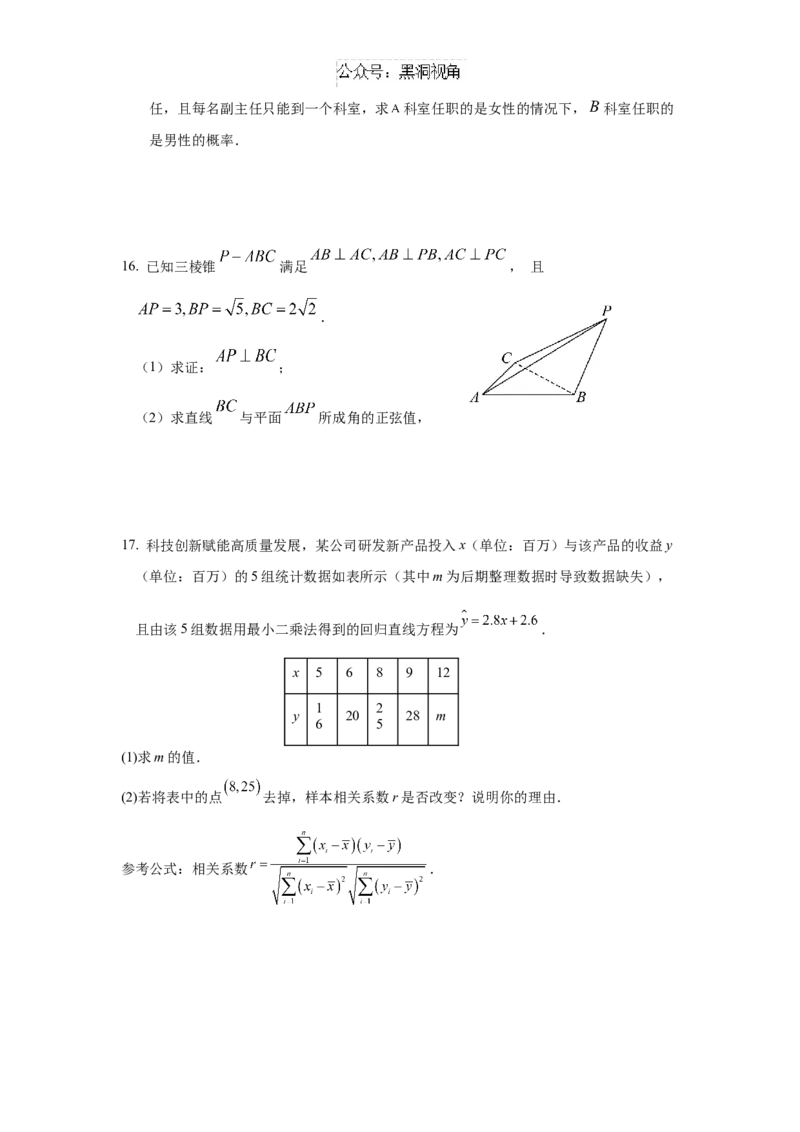
11. 双纽线,也称伯努利双纽线.如图,双纽线 经过原点,且 上的点满足到点
的距离与到点 的距离之积为1,则( )
A.直线 与 只有1个公共点
B.圆 与 有4个公共点
C. 与 轴的交点坐标为
D. 上的点到 轴的距离的最大值为
三、填空题:本题共3小题,每小题5分,共15分.
12.在二项式 的展开式中,常数项为 .
13. .2024年7月14日13时,2024年巴黎奥运会火炬开始在巴黎传递,其中某段火炬传
递活动由包含甲、乙、丙在内的5名火炬手分四棒完成,若甲传递第一棒,最后一棒由
2名火炬手共同完成,且乙、丙不共同传递火炬,则不同的火炬传递方案种数为 .
14.已知双曲线 的左、右焦点分别为 ,离心率为2,过点 的
直线 交 的左支于 两点. ( 为坐标原点),记点 到直线 的距离为 ,
则 .
四、解答题:本题共5小题,共77分.请在答题卡指定区域内作答,解答时应写出文
字说明、证明过程或演算步骤.
15. 某单位准备从8名报名者(其中男性5人,女性3人)中选4人参加4个副主任职位竞
选.
(1)求所选4人中女性人数为2人的概率;
(2)若选出的4名副主任分配到 , , , 这4个科室上任,一个科室分配1名副主任,且每名副主任只能到一个科室,求 科室任职的是女性的情况下, 科室任职的
是男性的概率.
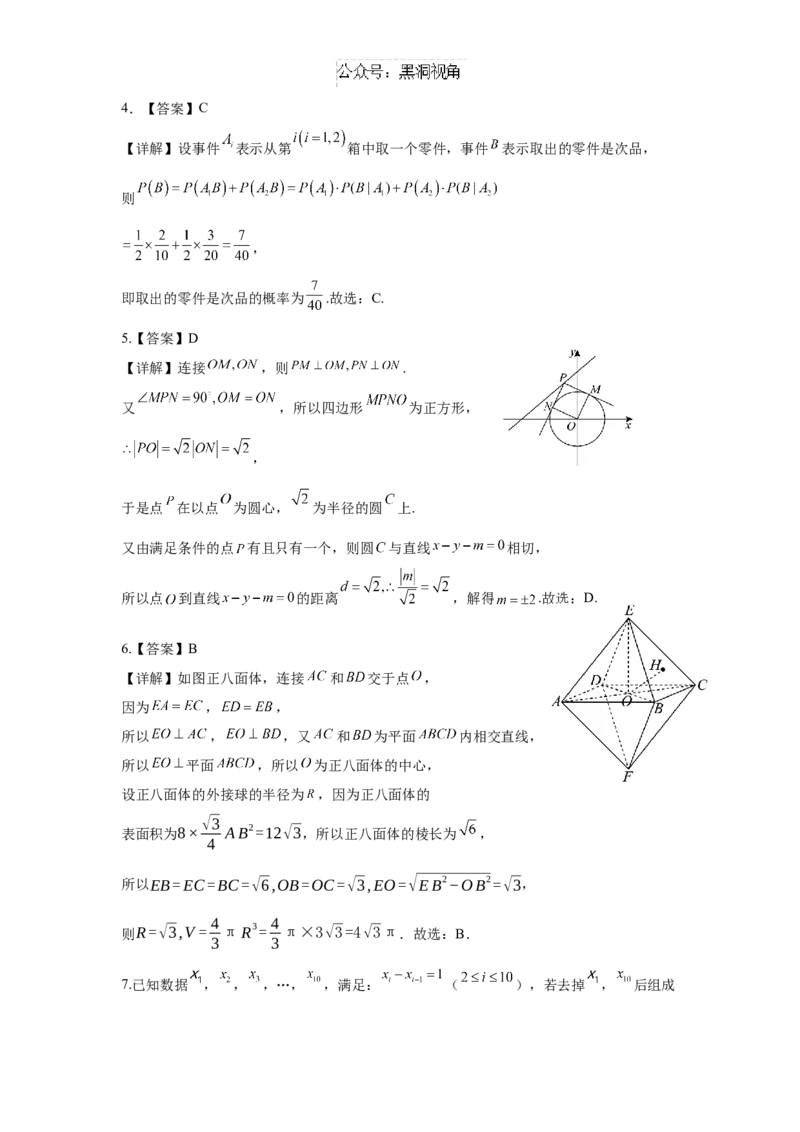
16. 已知三棱锥 满足 , 且
.
(1)求证: ;
(2)求直线 与平面 所成角的正弦值,
17. 科技创新赋能高质量发展,某公司研发新产品投入x(单位:百万)与该产品的收益y
(单位:百万)的5组统计数据如表所示(其中m为后期整理数据时导致数据缺失),
且由该5组数据用最小二乘法得到的回归直线方程为 .
x 5 6 8 9 12
1 2
y 20 28 m
6 5
(1)求m的值.
(2)若将表中的点 去掉,样本相关系数r是否改变?说明你的理由.
参考公式:相关系数 .18.已知函数 .
(1)判断函数 的零点个数,并说明理由;
(2)求曲线y=f (x)与y=g(x)的所有公切线方程.
19. 已知椭圆 的长轴长为4, , 为C的左、右焦点,点P(不
在x轴上)在C上运动,且 的最小值为 .
(1)求椭圆C的方程;
(2)过 的直线l与椭圆C交于不同的两点M,N,记 的内切圆的半径为r,求r的
取值范围.
江苏省如皋中学 2024-2025 学年度第一学期综合练习(一)
数学答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.【答案】C
【详解】因为 ,所以 ,代入 ,可得 ,
所以方程变为 ,可解得 或3,所以 ,故选:C.
2. B
3.【答案】A【详解】不同的报名方法种数有 .故选:A.4.【答案】C
【详解】设事件 表示从第 箱中取一个零件,事件 表示取出的零件是次品,
则
,
即取出的零件是次品的概率为 .故选:C.
5.【答案】D
【详解】连接 ,则 .
又 ,所以四边形 为正方形,
,
于是点 在以点 为圆心, 为半径的圆 上.
又由满足条件的点 有且只有一个,则圆 与直线 相切,
所以点 到直线 的距离 ,解得 .故选:D.
6.【答案】B
【详解】如图正八面体,连接 和 交于点 ,
因为 , ,
所以 , ,又 和 为平面 内相交直线,
所以 平面 ,所以 为正八面体的中心,
设正八面体的外接球的半径为 ,因为正八面体的
√3
表面积为8× AB2=12√3,所以正八面体的棱长为 ,
4
所以EB=EC=BC=√6,OB=OC=√3,EO=√EB2−OB2=√3,
4 4
则R=√3,V = πR3= π×3√3=4√3π.故选:B.
3 3
7.已知数据 , , ,…, ,满足: ( ),若去掉 , 后组成一组新数据,则新数据与原数据相比,下列说法错误的是( )
A.中位数不变 B.第35百分位数不变
C.平均数不变 D.方差不变
【答案】D
【详解】原来的中位数与现在的中位数均为 ,故中位数不变,故
A选项正确;原数据中, ,第35百分位数是第4个数据 ,
去掉 , 后, ,第35百分位数是新数据中的第3个 ,
第35百分位数不变,B选项正确;
原来的平均数为 ,
去 , 掉后的平均数为 ,平均数不变,故C选项正确;
原来的方差为 ,
去掉后 , 的方差为 ,
方差变小,故D选项错误.故选:D.
8. 【答案】D
【详解】因为 ,令 ,则 ,
则 ,再令 ,代入上式可得 ,
所以 ,故选:D.
9. 【答案】BD
10. 【答案】AD
【详解】设 ,原式为 ,令 , ,A正确;
令 ,则 ,
同乘 得 ,
, ,故B错误
令 ,则 ,故C错误
两边同时求导得: ,
再令 , ,故D正确.故选:AD.
11. 【答案】ACD
【详解】设曲线 上的动点 ,则 ,
化简得 ,令 ,解得 或 ,
因此双纽线 与 轴的交点坐标为 , ,C正确;
由 ,解得 ,因此直线 与 只有1个公共点,A正确;
由 ,解得 或 ,因此圆 与 有2个公共点,
B错误;
由 ,得 ,则 ,
令 ,则 ,
因此 ,当且仅当 时取等号,即 上的点到 轴的距离的最大值为 ,D正
确.故选:ACD三、填空题:本题共3小题,每小题5分,共15分.
12.在二项式 的展开式中,常数项为 . 180
13. 【答案】10
【详解】最后一棒可以是除甲、乙、丙之外的2人,也可以是从乙、丙中选1人,从除甲、
乙、丙之外的2人中选1人组成,所以最后一棒的安排方案有: 种;
安排最后一棒后,剩余两人安排在中间两棒,方案有: 种,
由分步计数乘法原理,不同的传递方案种数为: 种.
故答案为:10
14.【答案】
【详解】令双曲线 的半焦距为 ,由离心率为2,得 ,
取 的中点 ,连接 ,由 ,得 ,则 ,
连接 ,由 为 的中点,得 , , ,
因此 ,即 ,整理得 ,
而 ,所以 .
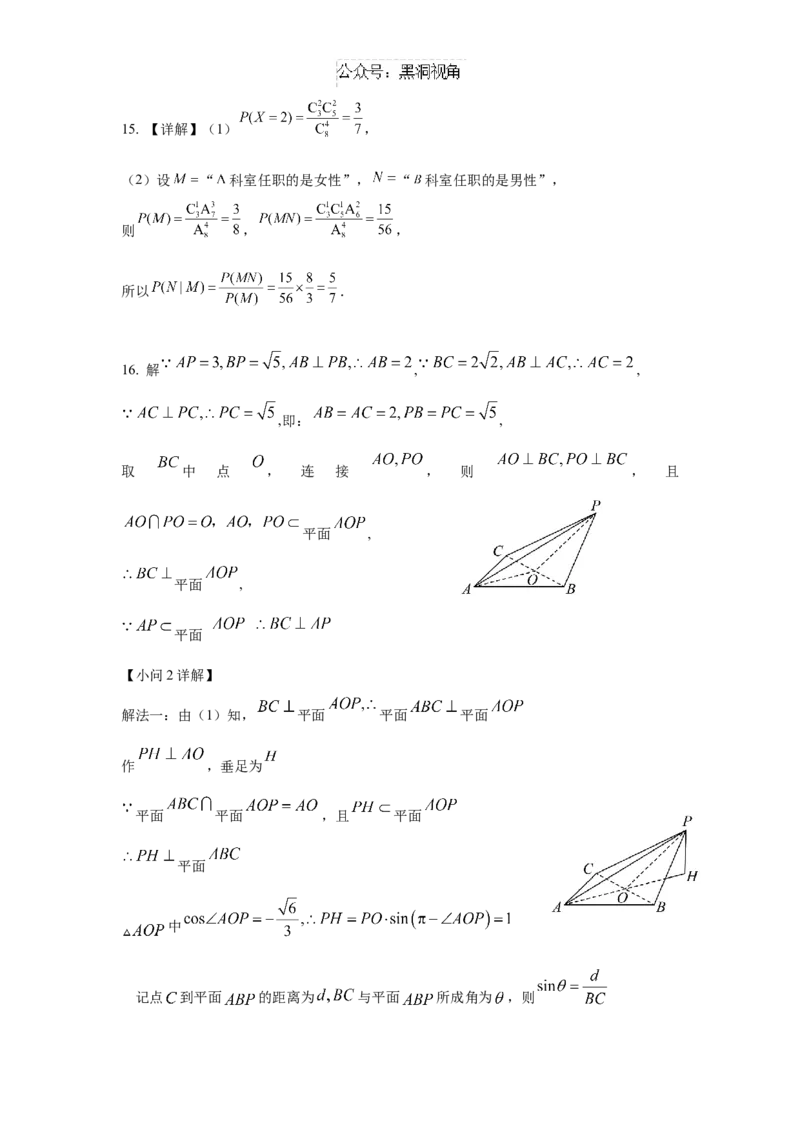
故答案为:15. 【详解】(1) ,
(2)设 “ 科室任职的是女性”, “ 科室任职的是男性”,
则 , ,
所以 .
16. 解 , ,
,即: ,
取 中 点 , 连 接 , 则 , 且
平面 ,
平面 ,
平面
【小问2详解】
解法一:由(1)知, 平面 平面 平面
作 ,垂足为
平面 平面 ,且 平面
平面
中
记点 到平面 的距离为 与平面 所成角为 ,则由 得:
因此,
解法二:如图,以 为坐标原点, 所在直线分别为 轴建立空间直角坐标系
由(1)可知
中,
设 的法向量
由 得: 取
记 与平面 所成角为 .则 .
17.参考公式:相关系数 .
【详解】(1)由题意可知, ,
,所以样本中心为 ,将点 代入 ,可得 ,
解得 .
(2)由(1)可得,样本中心为 ,所以 , .
由相关系公式知, ,将点 去掉后,样本相关系数r不变
18.已知函数 .
(1)判断函数 的零点个数,并说明理由;
(2)求曲线y=f (x)与y=g(x)的所有公切线方程.
解:函数 的定义域为: ,
, 在单调递增
又 , 存在唯一零点,在 之间.
【小问2详解】 ,
以 上的点 为切点的切线方程为
以 上的点 为切点的切线方程为:
令则 ,得 ,即 .
设 ,函数 ,则 .
当 时, 单调递减,当 时, 单调递增, ,
的解为 ,又 .
和 存在唯一一条公切线为 .
19. 【详解】(1)由题意得 ,设 , 的长分别为m,n, ,
则在 中,由余弦定理可得
当且仅当 时取等号,从而 ,得 ,∴ ,
所以椭圆的标准方程为 .
(2)设 , ,
由题意,根据椭圆的定义可得 的周长为 ,
,所以 ,
设l的方程为 ,联立椭圆方程 ,
整理可得 ,易知
且 , ,,
所以 ,令 ,则 ,
,令函数 ,则 在 上单
调递增,则 ,所以 ,即 ,故r的取值范围为 .