文档内容
2020年辽宁省盘锦市中考数学试卷
一、单选题(下列各题的备选答案中.只有一个是正确的,请将正确答案的序号涂在答题
卡上,每小题3分,共30分)
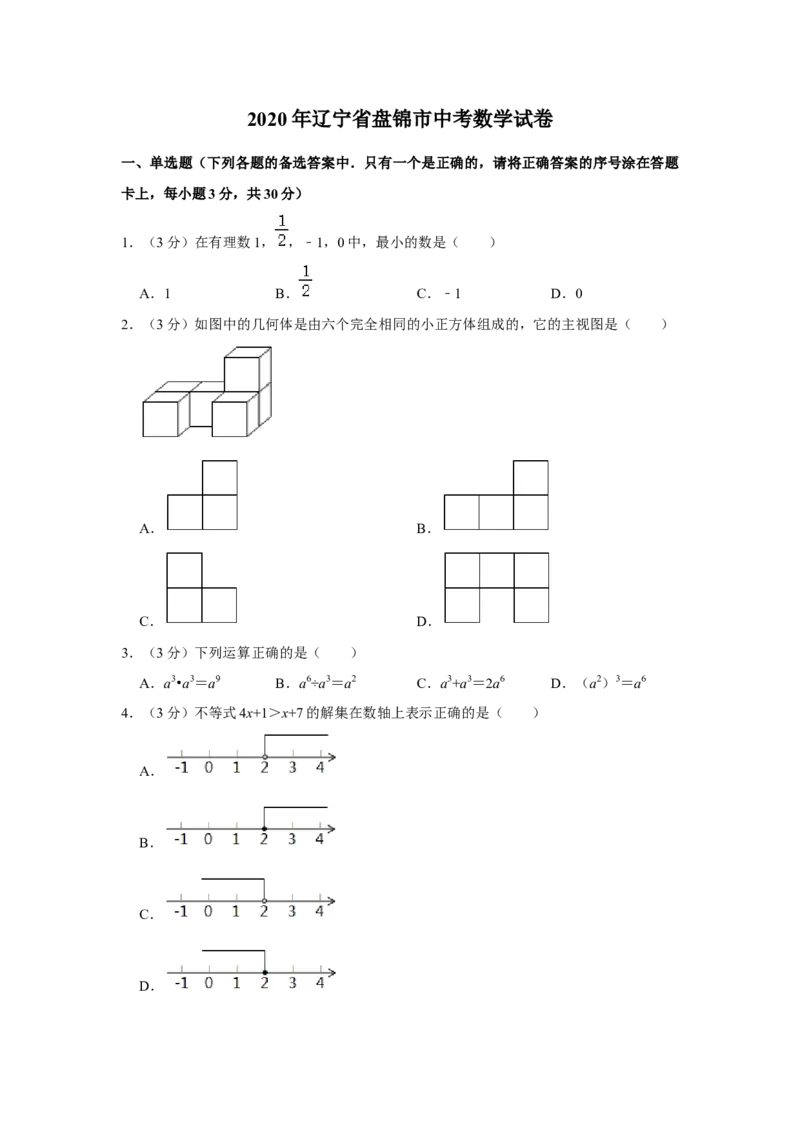
1.(3分)在有理数1, ,﹣1,0中,最小的数是( )
A.1 B. C.﹣1 D.0
2.(3分)如图中的几何体是由六个完全相同的小正方体组成的,它的主视图是( )
A. B.
C. D.
3.(3分)下列运算正确的是( )
A.a3•a3=a9 B.a6÷a3=a2 C.a3+a3=2a6 D.(a2)3=a6
4.(3分)不等式4x+1>x+7的解集在数轴上表示正确的是( )
A.
B.
C.
D.5.(3分)下列命题正确的是( )
A.圆内接四边形的对角互补
B.平行四边形的对角线相等
C.菱形的四个角都相等
D.等边三角形是中心对称图形
6.(3分)为了解某地区九年级男生的身高情况,随机抽取了该地区 1000名九年级男生
的身高数据,统计结果如下:
身高x/cm x<160 160≤x<170 170≤x<180 x≥180
人数 60 260 550 130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于170cm的概
率是( )
A.0.32 B.0.55 C.0.68 D.0.87
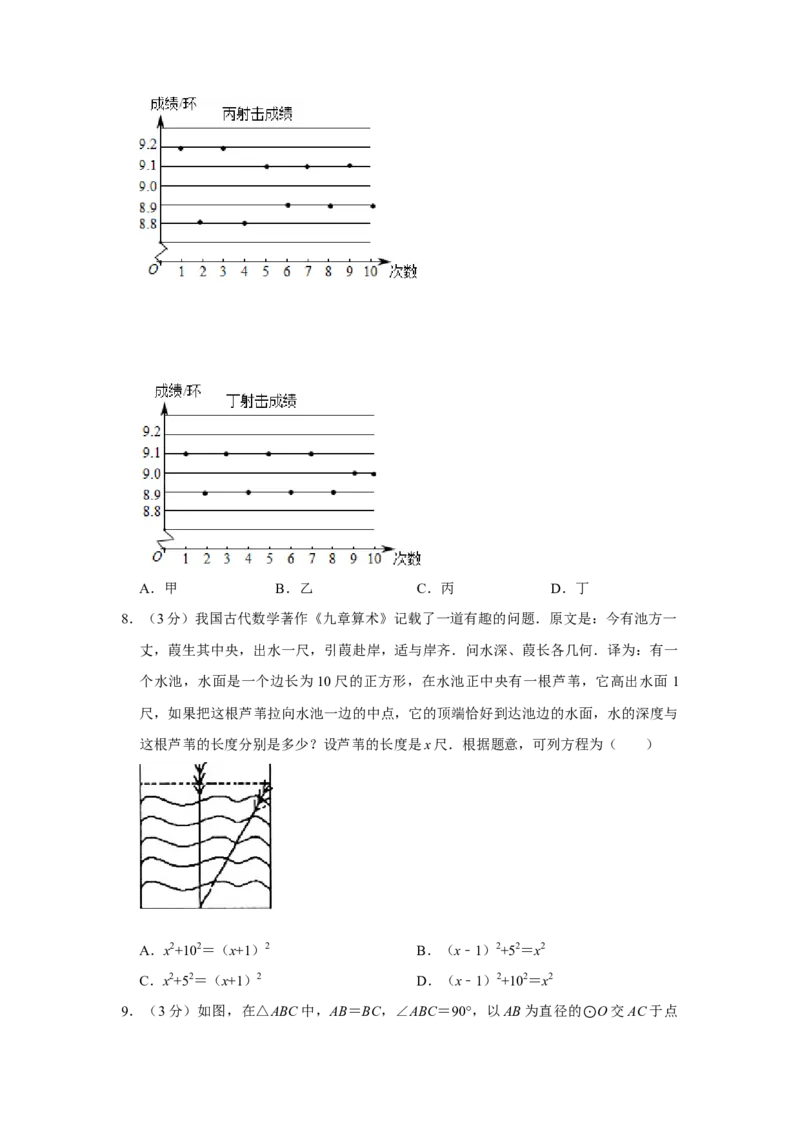
7.(3分)在市运动会射击比赛选拔赛中,某校射击队甲、乙、丙、丁四名队员的 10次
射击成绩如图所示.他们的平均成绩均是9.0环,若选一名射击成绩稳定的队员参加比
赛,最合适的人选是( )A.甲 B.乙 C.丙 D.丁
8.(3分)我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一
丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一
个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面 1
尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与
这根芦苇的长度分别是多少?设芦苇的长度是x尺.根据题意,可列方程为( )
A.x2+102=(x+1)2 B.(x﹣1)2+52=x2
C.x2+52=(x+1)2 D.(x﹣1)2+102=x2
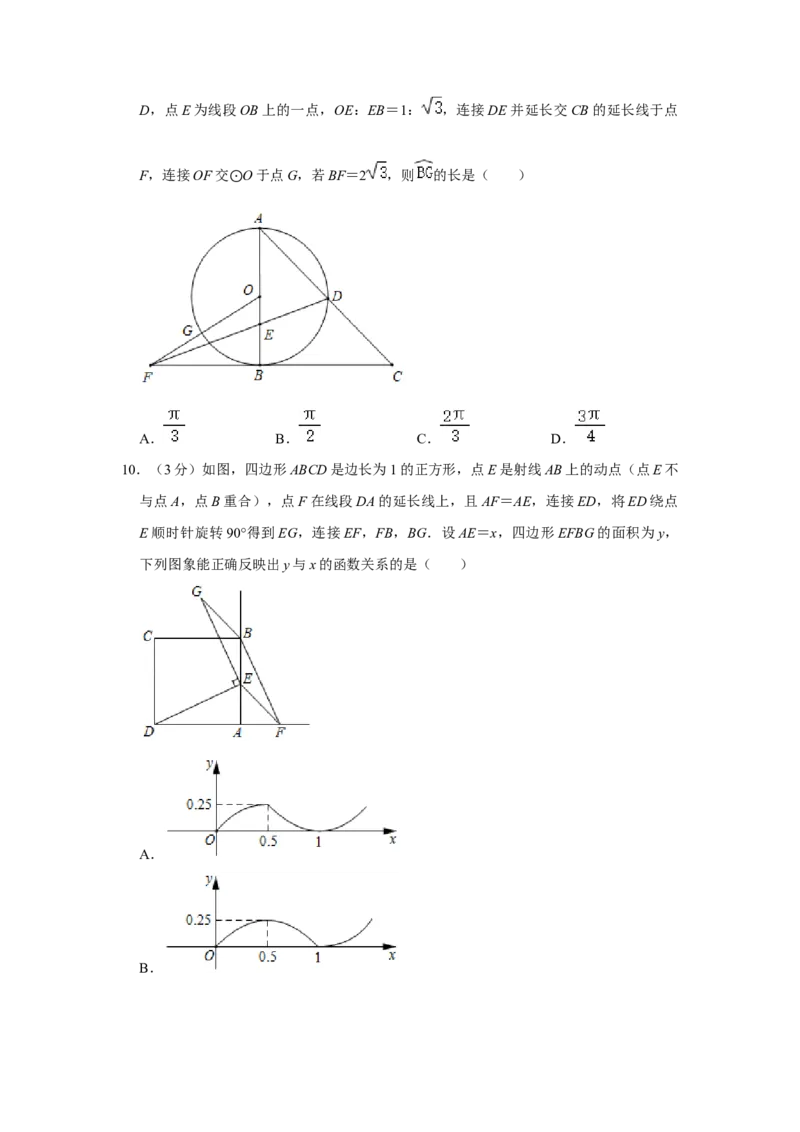
9.(3分)如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的 O交AC于点
⊙D,点E为线段OB上的一点,OE:EB=1: ,连接DE并延长交CB的延长线于点
F,连接OF交 O于点G,若BF=2 ,则 的长是( )
⊙
A. B. C. D.
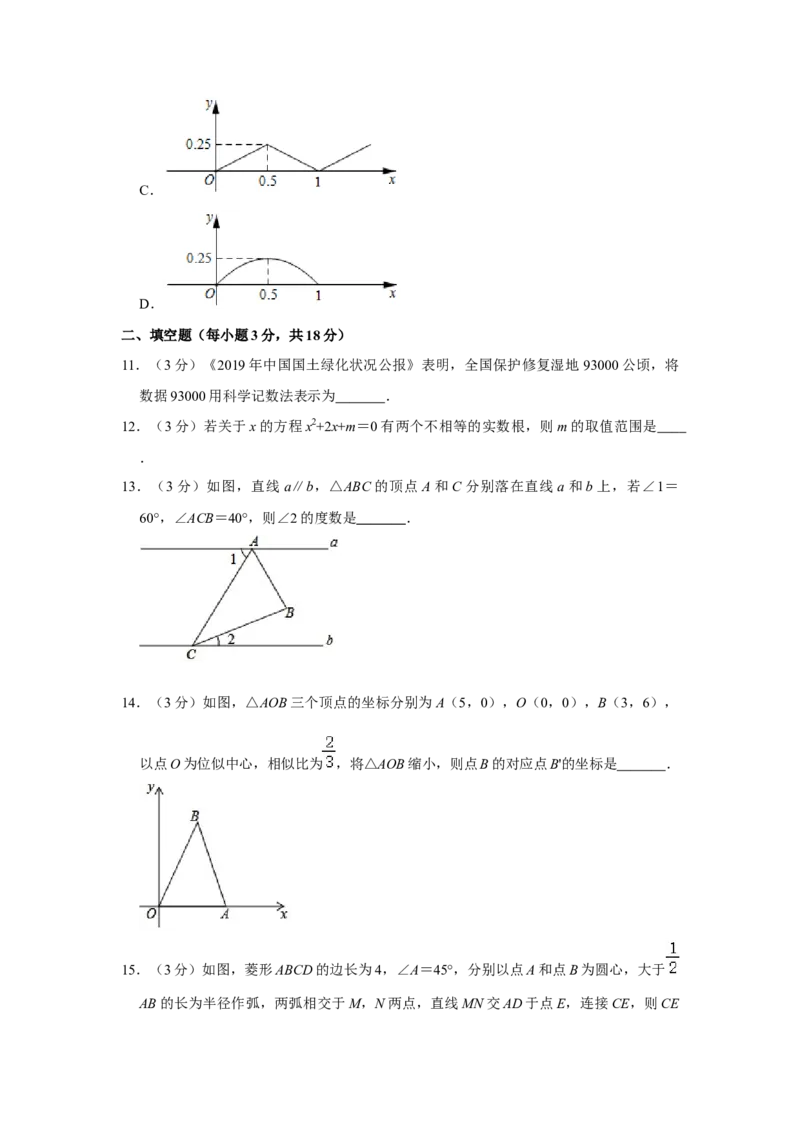
10.(3分)如图,四边形ABCD是边长为1的正方形,点E是射线AB上的动点(点E不
与点A,点B重合),点F在线段DA的延长线上,且AF=AE,连接ED,将ED绕点
E顺时针旋转90°得到EG,连接EF,FB,BG.设AE=x,四边形EFBG的面积为y,
下列图象能正确反映出y与x的函数关系的是( )
A.
B.C.
D.
二、填空题(每小题3分,共18分)
11.(3分)《2019年中国国土绿化状况公报》表明,全国保护修复湿地 93000公顷,将
数据93000用科学记数法表示为 .
12.(3分)若关于x的方程x2+2x+m=0有两个不相等的实数根,则m的取值范围是
.
13.(3分)如图,直线 a∥b,△ABC的顶点A和C分别落在直线a和b上,若∠1=
60°,∠ACB=40°,则∠2的度数是 .
14.(3分)如图,△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),
以点O为位似中心,相似比为 ,将△AOB缩小,则点B的对应点B'的坐标是 .
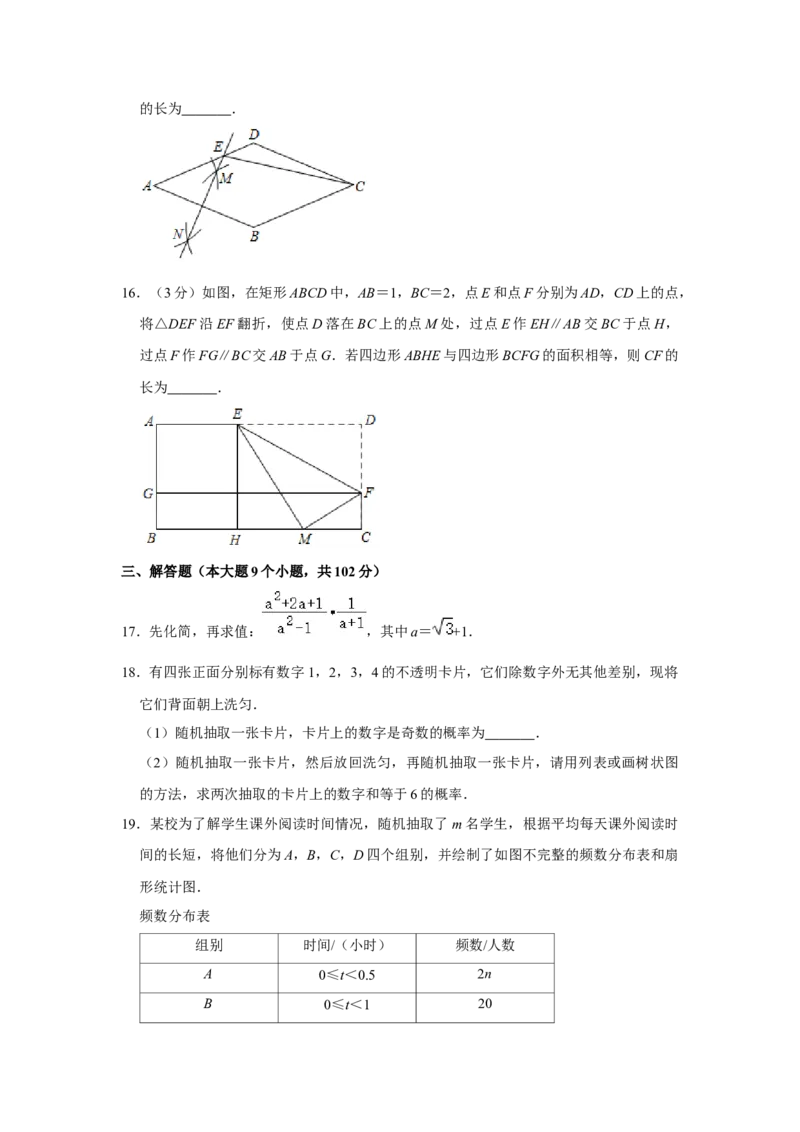
15.(3分)如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于
AB的长为半径作弧,两弧相交于M,N两点,直线MN交AD于点E,连接CE,则CE的长为 .
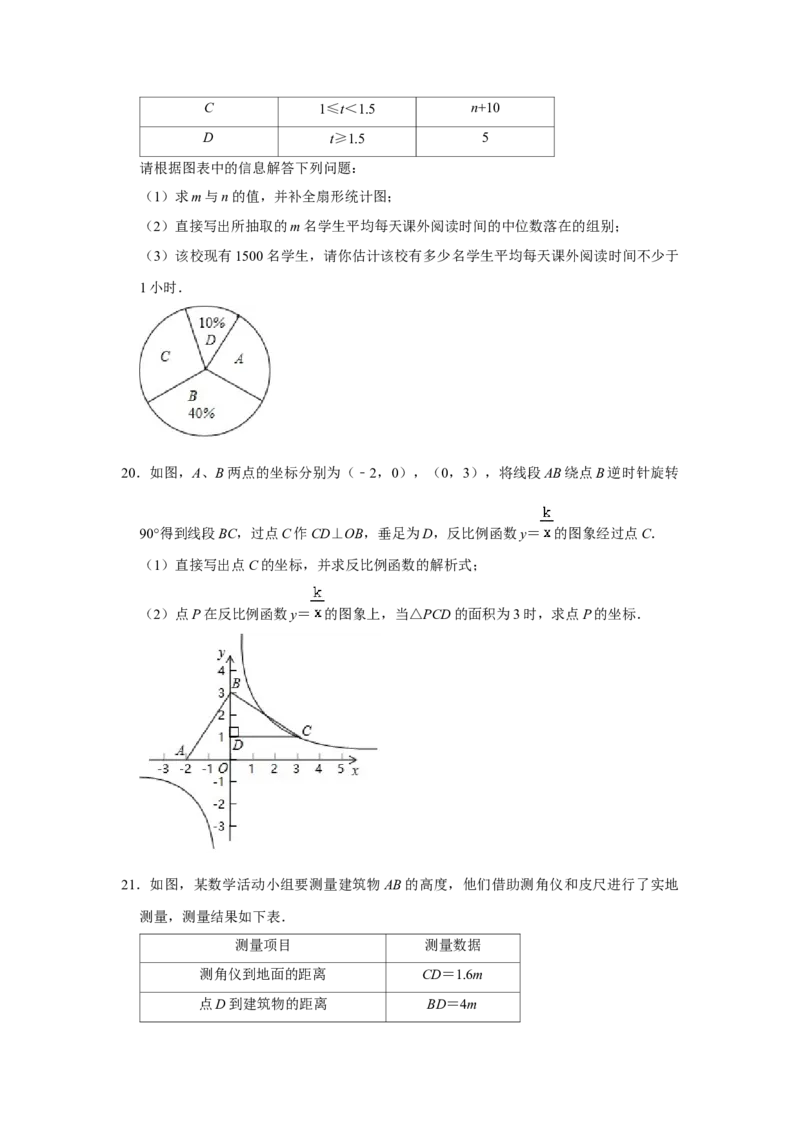
16.(3分)如图,在矩形ABCD中,AB=1,BC=2,点E和点F分别为AD,CD上的点,
将△DEF沿EF翻折,使点D落在BC上的点M处,过点E作EH∥AB交BC于点H,
过点F作FG∥BC交AB于点G.若四边形ABHE与四边形BCFG的面积相等,则CF的
长为 .
三、解答题(本大题9个小题,共102分)
17.先化简,再求值: ,其中a= +1.
18.有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外无其他差别,现将
它们背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是奇数的概率为 .
(2)随机抽取一张卡片,然后放回洗匀,再随机抽取一张卡片,请用列表或画树状图
的方法,求两次抽取的卡片上的数字和等于6的概率.
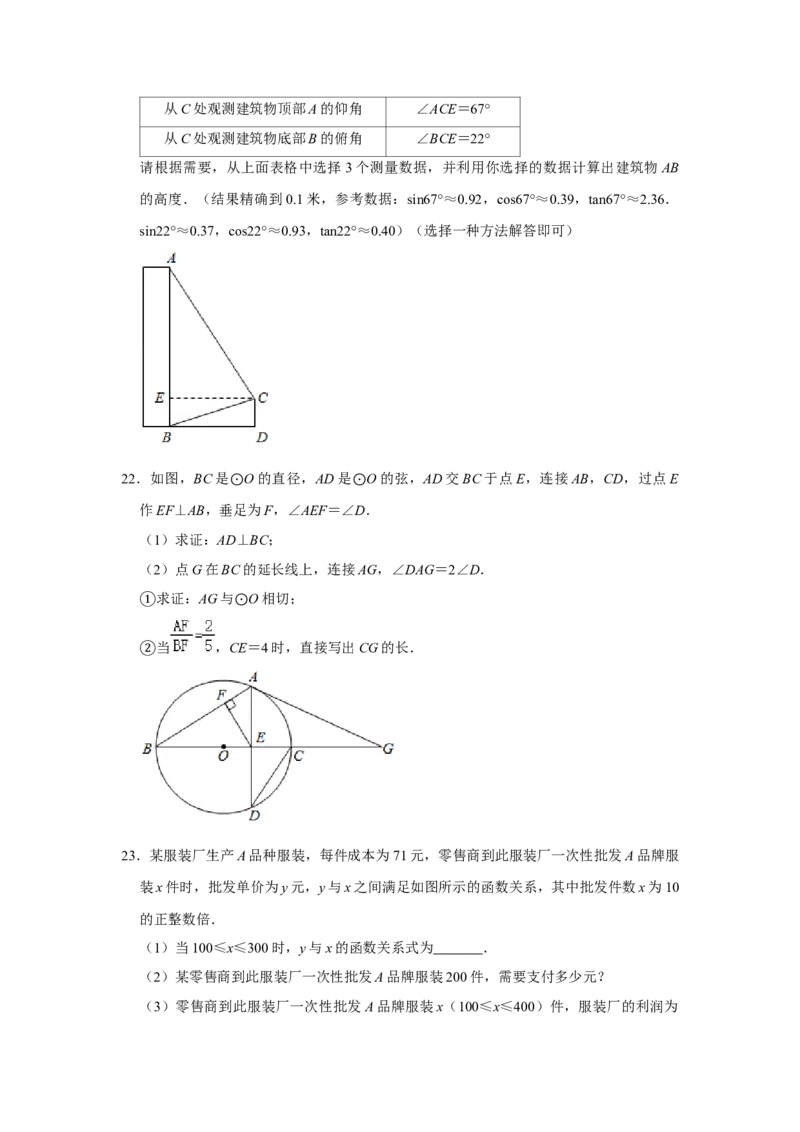
19.某校为了解学生课外阅读时间情况,随机抽取了m名学生,根据平均每天课外阅读时
间的长短,将他们分为A,B,C,D四个组别,并绘制了如图不完整的频数分布表和扇
形统计图.
频数分布表
组别 时间/(小时) 频数/人数
A 0≤t<0.5 2n
B 0≤t<1 20C 1≤t<1.5 n+10
D t≥1.5 5
请根据图表中的信息解答下列问题:
(1)求m与n的值,并补全扇形统计图;
(2)直接写出所抽取的m名学生平均每天课外阅读时间的中位数落在的组别;
(3)该校现有1500名学生,请你估计该校有多少名学生平均每天课外阅读时间不少于
1小时.
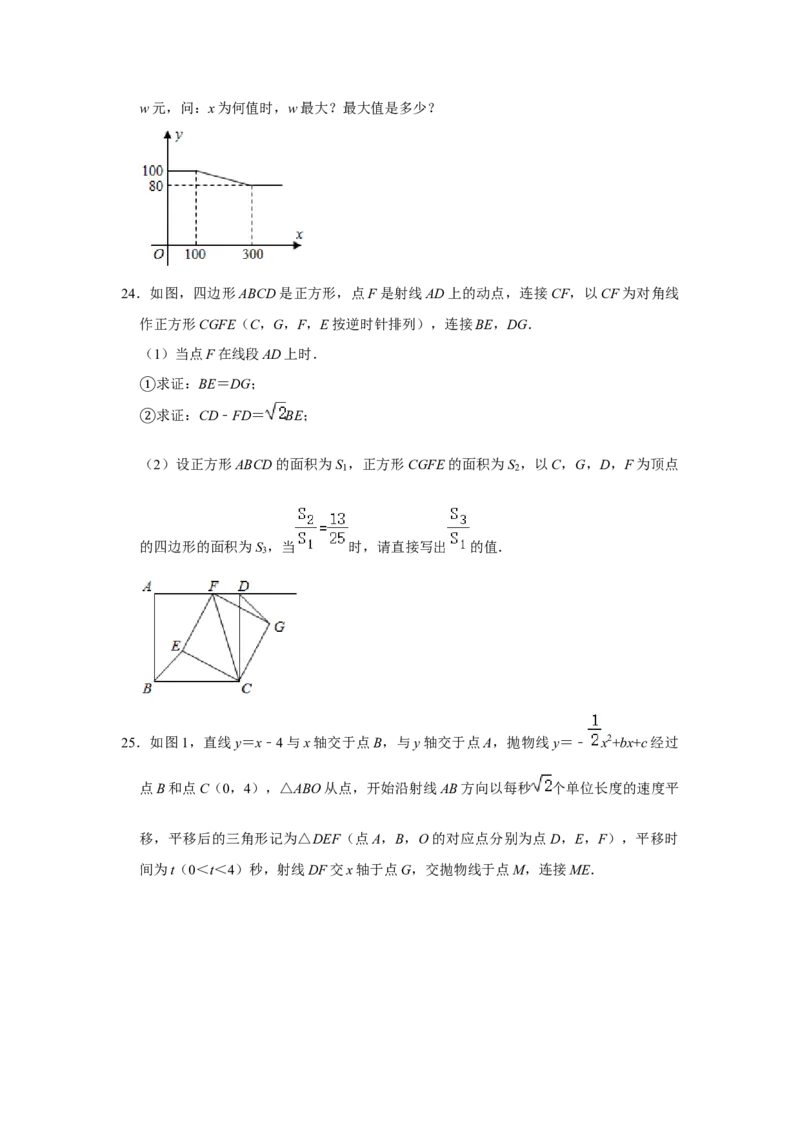
20.如图,A、B两点的坐标分别为(﹣2,0),(0,3),将线段AB绕点B逆时针旋转
90°得到线段BC,过点C作CD⊥OB,垂足为D,反比例函数y= 的图象经过点C.
(1)直接写出点C的坐标,并求反比例函数的解析式;
(2)点P在反比例函数y= 的图象上,当△PCD的面积为3时,求点P的坐标.
21.如图,某数学活动小组要测量建筑物AB的高度,他们借助测角仪和皮尺进行了实地
测量,测量结果如下表.
测量项目 测量数据
测角仪到地面的距离 CD=1.6m
点D到建筑物的距离 BD=4m从C处观测建筑物顶部A的仰角 ∠ACE=67°
从C处观测建筑物底部B的俯角 ∠BCE=22°
请根据需要,从上面表格中选择3个测量数据,并利用你选择的数据计算出建筑物AB
的高度.(结果精确到0.1米,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36.
sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)(选择一种方法解答即可)
22.如图,BC是 O的直径,AD是 O的弦,AD交BC于点E,连接AB,CD,过点E
作EF⊥AB,垂⊙足为F,∠AEF=∠⊙D.
(1)求证:AD⊥BC;
(2)点G在BC的延长线上,连接AG,∠DAG=2∠D.
求证:AG与 O相切;
① ⊙
当 ,CE=4时,直接写出CG的长.
②
23.某服装厂生产A品种服装,每件成本为71元,零售商到此服装厂一次性批发A品牌服
装x件时,批发单价为y元,y与x之间满足如图所示的函数关系,其中批发件数x为10
的正整数倍.
(1)当100≤x≤300时,y与x的函数关系式为 .
(2)某零售商到此服装厂一次性批发A品牌服装200件,需要支付多少元?
(3)零售商到此服装厂一次性批发A品牌服装x(100≤x≤400)件,服装厂的利润为w元,问:x为何值时,w最大?最大值是多少?
24.如图,四边形ABCD是正方形,点F是射线AD上的动点,连接CF,以CF为对角线
作正方形CGFE(C,G,F,E按逆时针排列),连接BE,DG.
(1)当点F在线段AD上时.
求证:BE=DG;
①求证:CD﹣FD= BE;
②
(2)设正方形ABCD的面积为S ,正方形CGFE的面积为S ,以C,G,D,F为顶点
1 2
的四边形的面积为S ,当 时,请直接写出 的值.
3
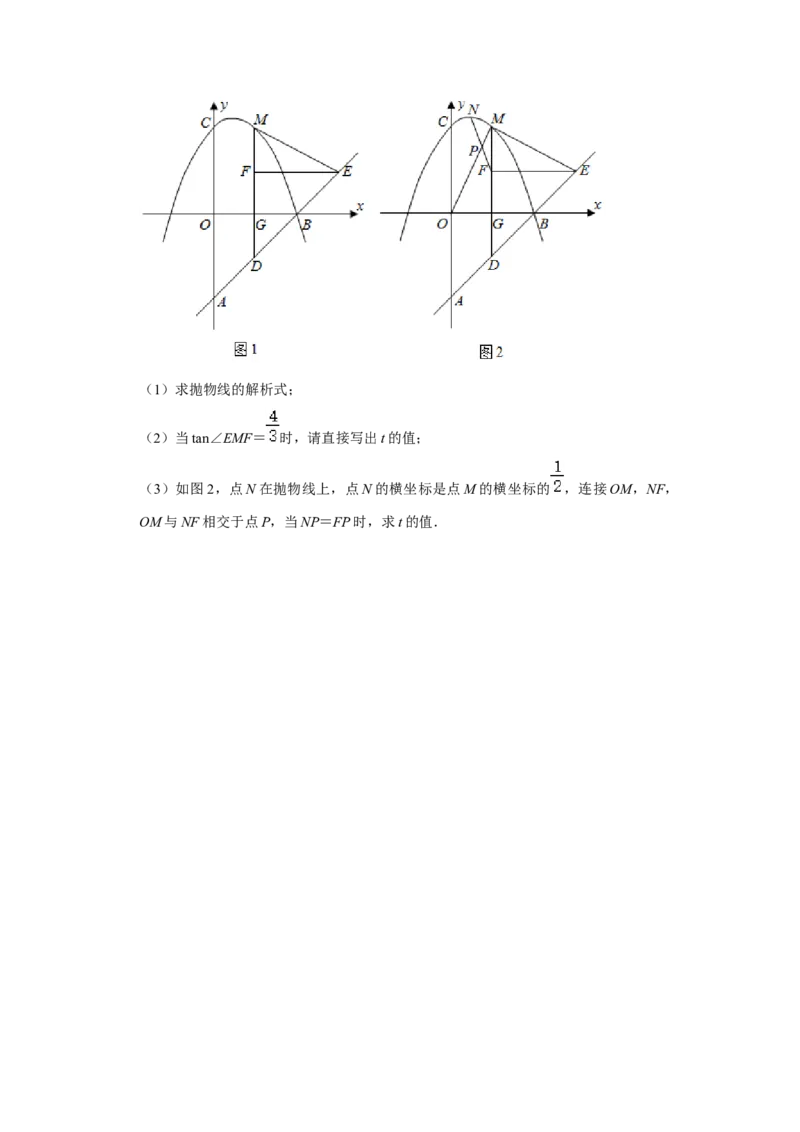
25.如图1,直线y=x﹣4与x轴交于点B,与y轴交于点A,抛物线y=﹣ x2+bx+c经过
点B和点C(0,4),△ABO从点,开始沿射线AB方向以每秒 个单位长度的速度平
移,平移后的三角形记为△DEF(点A,B,O的对应点分别为点D,E,F),平移时
间为t(0<t<4)秒,射线DF交x轴于点G,交抛物线于点M,连接ME.(1)求抛物线的解析式;
(2)当tan∠EMF= 时,请直接写出t的值;
(3)如图2,点N在抛物线上,点N的横坐标是点M的横坐标的 ,连接OM,NF,
OM与NF相交于点P,当NP=FP时,求t的值.