文档内容
2024 年高考押题预测卷 02【新九省卷】
数学·参考答案
第一部分(选择题 共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1 2 3 4 5 6 7 8
D B A C D D C D
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9 10 11
AC AC AD
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
13.11 13. 14.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.(本小题满分13分)
【解】(1)由于 的斜率为 ,所以 ,
又 ,故 ,解得 ,
(2)由(1)知 ,所以 ,
故当 时, 单调递增,
当 时, 单调递减,
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故当 时, 取最小值 ,
要使 恒成立,故 ,解得 ,
故 的取值范围为
16.(本小题满分15分)
【解】(1)由题知:各组频率分别为:0.15,0.25,0.3,0.2,0.1,
日均阅读时间的平均数为:
(分钟)
(2)由题意,在[60,80),[80,100),[100,120]三组分别抽取3,2,1人
的可能取值为:0,1,2
则
所以 的分布列为:
0 1 2
17.(本小题满分15分)
【解】(1)连接 交 与点 ,连接 ,可得平面 与平面 的交线为 ,
因为 平面 , 平面 ,所以 ,
又因为 为 的中点,所以点 为 的中点,
取 的中点 ,连接 ,可得 且 ,
又因为 为 的中点,可得 且 ,
所以 且 ,所以四边形 为平行四边形,所以 ,
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司又因为 平面 ,且 平面 ,所以 平面 .
(2)取 的中点 ,连结 ,
因为 ,可得 ,且 ,
又因为 ,且 ,
所以 ,所以 ,
又因为 ,且 平面 ,所以 平面 ,
以 为坐标原点,建立如图所示的空间直角坐标系 ,
可得 ,
因为 为 的中点, 为 的中点,可得 ,
则 ,
设 是平面 的法向量,则 ,
取 ,可得 ,所以 ,
设 是平面 的法向量,则 ,
取 ,可得 ,所以 ;
设平面 与平面 的夹角为 ,则 ,
即平面 与平面 的夹角的余弦值为 .
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司18.(本小题满分17分)
【解】(1)①当直线l斜率不存在时,由椭圆的对称性,不妨设直线l在y轴右侧,
直线OA的方程为 ,
由 ,解得 , ,所以, ,
所以,直线AB的方程为 ,此时 .
同理,当直线l在y轴左侧时, .
②当直线l斜率存在时,设直线l的方程为 , , ,
由 消去y整理得, ,
∴ ,且 , ,
又∵ ,∴ 即: ,
所以, ,
则 ,
故 ,
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 满足 ,
所以, .
综上, ,所以,点P的轨迹方程为 .
(2)①由(1)可知,当直线l斜率不存在或斜率为0时, .
②当直线l斜率存在且不为0时,
,
∵ ,∴ ,当且仅当 ,即 等号成立.
∴ ,∴ ,
∴ ,
综上, .
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司19.(本小题满分17分)
【解】(1) ,
由题意可知 ;
(2)解法一:①若 ,则 为恒等置换;
②若存在两个不同的 ,使得 ,不妨设 ,则 .
所以 ,即 为恒等置换;
③若存在唯一的 ,使得 ,不妨设 ,则 或 .
当 时,由(1)可知 为恒等置换;
同理可知,当 时, 也是恒等置换;
④若对任意的 ,
则情形一: 或 或 ;
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司情形二: 或 或
或 或 或 ;
对于情形一: 为恒等置换;
对于情形二: 为恒等置换;
综上,对任意 ,存在 ,使得 为恒等置换;
解法二:对于任意 ,都有 ,
所以 中,至少有一个满足 ,
即使得 的 的取值可能为 .
当 分别取 时,记使得 的 值分别为 ,
只需取 为 的最小公倍数即可.
所以对任意 ,存在 ,使得 为恒等置换;
(3)不妨设原始牌型从上到下依次编号为1到52,则洗牌一次相当于对 作一次如下置换:
,即
其中 .
注意到各编号在置换中的如下变化:
, ,
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司,
,
,
,
,
,
,
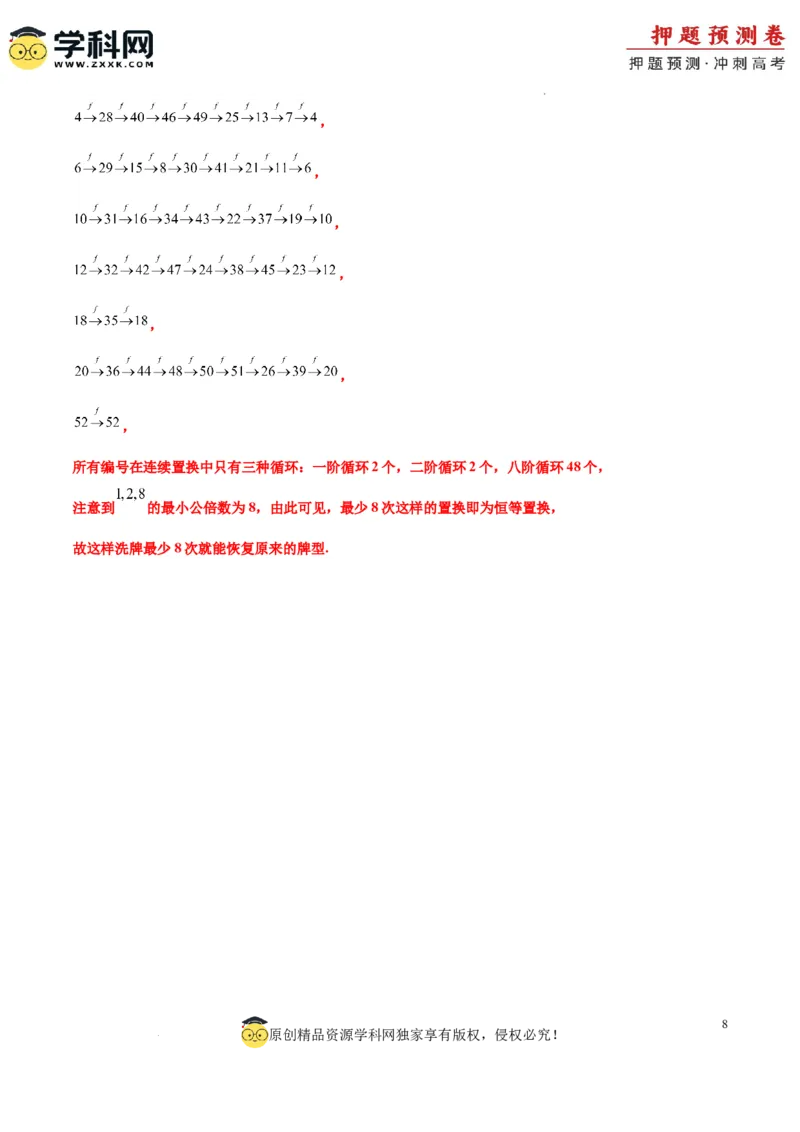
所有编号在连续置换中只有三种循环:一阶循环2个,二阶循环2个,八阶循环48个,
注意到 的最小公倍数为8,由此可见,最少8次这样的置换即为恒等置换,
故这样洗牌最少8次就能恢复原来的牌型.
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司