文档内容
方法精讲-资料 3
(笔记)
主讲教师:焦点
授课时间:2024.05.01
粉笔公考·官方微信方法精讲-资料 3(笔记)
今日内容(P191-202)
第五节比重
第六节平均数
【注意】今日内容(P191-202):
1.第五节:比重。
2.第六节:平均数。
第五节 比重
关键字:占
题型
一、现期比重(必考,简单)
二、基期比重(考得很少,分析)
三、两期比重(常考,技巧强)
【注意】比重:非常高频的考点,在四川省考和国考中,考的都比较多。
1.关键字:占。
2.题型:根据时间的不同分为现期、基期、两期。
(1)现期比重(必考,简单)。
(2)基期比重(考的很少,分析)。
(3)两期比重(常考,技巧强)。
一、现期比重
题型识别:求现在,出现“占”
①A占B的比重:四川人口数占全国的比重
②在B中,A占的比重:在全国人口中,四川人口所占的比重
公式:比重=部分(A)/总体(B)
【注意】现期比重:
1.题型识别:求现在,出现“占”。在言语的表述上有两种表述形式:
1(1)A占B的比重:四川人口数占全国(人口)的比重。省略了“人口”,
是同意省略。
(2)在B中,A占的比重:在全国人口中,四川人口所占的比重。
2.公式:比重=部分(A)/总体(B)。如四川占全国的比重→四川/全国。
“比重=部分/整体”的三量变化
①求比重
比重=部分/整体
②求整体
整体=部分/比重
③求部分
部分=整体*比重
【注意】“比重=部分/整体”的三量变化:
1.求比重:比重=部分/整体。
2.求整体:已知部分、比重,求整体,整体=部分/比重。
3.求部分:已知整体、比重,求部分,部分=整体*比重。
【例1】(2020四川下)2017年末,国有单位和城镇集体单位城镇就业人员
约占全国城镇就业人员的:
A.13% B.15%
C.17% D.19%
2【解析】1.问题时间和材料时间一致,现期时间,出现“占”→现期比重。
“占”前是部分,国有单位和城镇集体单位城镇就业人员约→部分,“占”后是
总体,全国城镇就业人员→总体,定位图表找数据,所求=部分/总体=(6064+406)
/42462,计算之前看选项,选项差距大,分母截两位估算即可,式子变为6470/42,
首位商1,次位商5,对应B项。【选B】
【注意】
1.现期比重是四川的必考题,是最简单的送分题。
2.所求=部分/总体=(6064+406)/42462,若考虑用百化分的方法计算,需
要 对 百 化 分 非 常 敏 感 , 6064/42462 ≈ 1/7 ≈ 14.3% ,( 6064+406 )
/42462=6064/42462+406/42462≈14.3%+406/42462,结果是比14.3%大一丢丢,
但又不会大很多,因此选择B项。速算是非常灵活,只要能得出正确答案,怎么
做都行。
2021年,中国跨境电商交易规模达14.2万亿元,占我国货物进出口总额的
比例为36.3%。其中出口跨境电商交易规模11万亿元,同比增速13.4%;进口跨
境电商交易规模3.2万亿元,同比增速14.3%。2017~2022年第一季度,中国跨
境电商领域共发生262次投资,投资总金额654.91亿元。
【例2】(2023山东)2021年,我国全年的货物进出口总额约为多少万亿元?
A.36 B.39
C.42 D.45
【解析】2.问题时间和材料时间一致,现期时间,问“我国全年的货物进出
口总额”,读完题干之后发现没有“占”字,表面上看好像不是比重问题,但从
材料中可知“中国跨境电商交易规模达 14.2 万亿元,占我国货物进出口总额的
比例为36.3%”→已知部分、比重,求总体,总体=部分/比重=14.2/36.3%≈14.2/
(4*9%)≈14.2/(4*1/11)=14.2/(4÷11)=14.2*(11/4),不管小数点的情
况下,式子变为35*11,错位相加,结果为38.5,最接近B项,当选B项。【选
B】
3【注意】
1.总体=部分/比重=14.2/36.3%,算之前看选项,首位相同,次位差≤首位,
选项差距小,可以分母截三位计算。
2.总体=部分/比重=14.2/36.3%,A、B项首位相同,次位差等于首位,C、D
项首位相同,次位差小于首位,选项差距小,分母截三位,式子变为142/363,
首位商 3,次位商 9,对应 B项。本题中截三位计算相当于精算,能得出答案,
但是速度较慢,此时可以用百化分。若使用百化分计算,注意选项差距较小,36.3%
不能看成33.3%≈1/3。
3.错位相加,35*11=35+3.5=38.5。基期+0.1*基期是错位相加,一个数乘以
1.1是错位相加,忽略小数点,一个数乘以11,也是错位相加。
4.若考场上想不到用百化分的方法计算,可以直接用截位直除的方法。
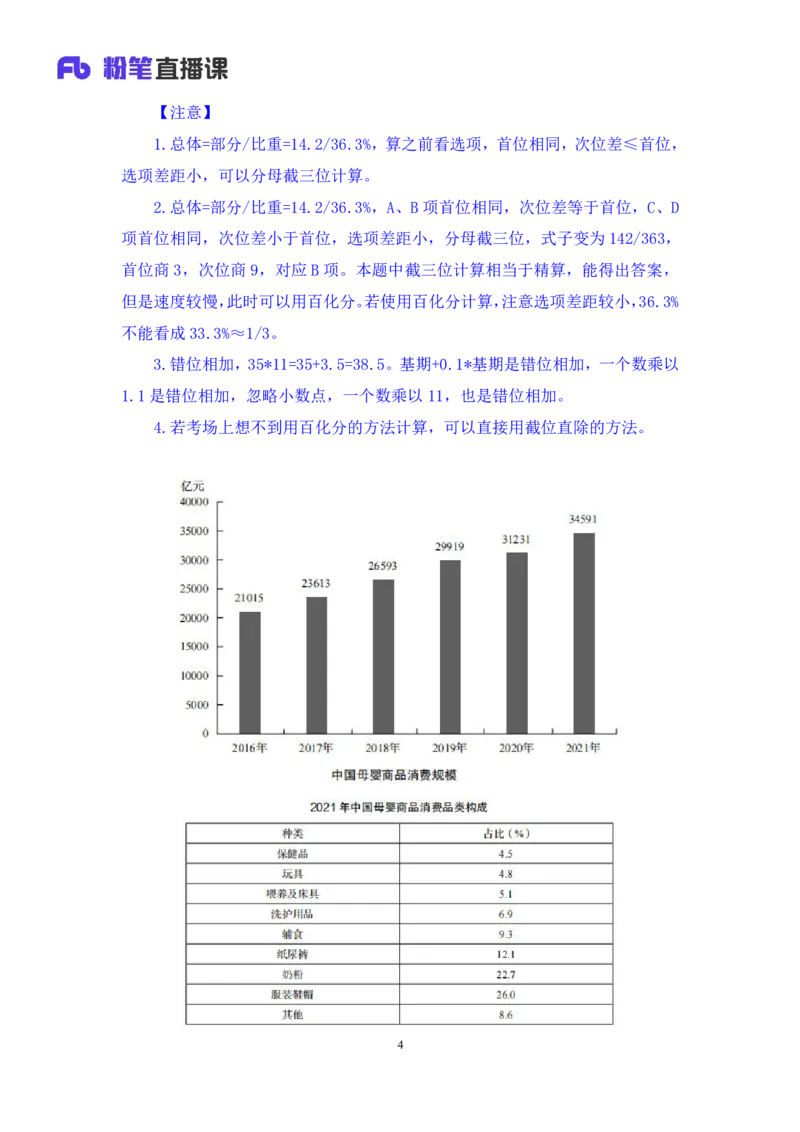
4【例3】(2023联考)2021年,我国消费最多的母婴商品金额约为:
A.9638亿元 B.8994亿元
C.7852亿元 D.4186亿元
【解析】3.问题时间和材料时间是有重合的,现期时间,问我国消费最多的
母婴商品金额,材料给的是母婴商品消费品类构成→即各母婴商品消费品类所占
比重→谁的比重占的最大,谁的钱就花的最多→找A求B题。占比最多的是服装
鞋帽,定位材料找数据,部分=总体*比重=34591*26%,选项首位各不相同,选项
差距大,26%近似看成25%=1/4,原式≈34591*(1/4)=8000+,对应B项。【选B】
【注意】26%什么时候可以看成 25%,两者之间本质的差别是在 26 或 25个
数里差了 1,相当于 20 多的数里面差了 1。此时要看选项(选项为王),选项差
距小,26%不能看成25%,选项差距大,26%可以近似看成25%。
概念引申(比重的特殊表述形式)
①利润率=利润/收入(资料分析)
②增长贡献率=部分的增长量/整体的增长量
2023年、2022年总收入分别是500元和400元,工资收入分别是350元和
300元。则:2023年工资收入对总收入的增长贡献率是多少?
【注意】概念引申(比重的特殊表述形式):
1.利润率=利润/收入(资料分析),在资料分析中的利润率一般默认的是收
入利润率;在数量关系中,利润率=利润/成本,是理想化的成本利润率。
2.增长贡献率=部分的增长量/整体的增长量。
(1)贡献率:如我的工资在我们家的贡献率→我的工资/全家的收入,我的
工资→部分,全家的收入→整体,贡献率=部分/整体。
(2)增长贡献率:求的是增长部分的比重,即增长量的比重,因此增长贡
献率的公式是部分的增长量/整体的增长量(本质也是部分/整体)。
3.例:2023年、2022年总收入分别是500元和400元,工资收入分别是350
元和300元。则:2023年工资收入对总收入的增长贡献率是多少?
5答:增长贡献率=部分的增长量/整体的增长量=(350-300)/(500-400)
=50/100=50%。
2020年前三季度,G 省智能机器人产业实现营业收入 326.62 亿元,同比增
长超40%,四大行业营业收入均实现正增长,经济效益好于全部规模以上工业企
业。
【例4】(2021广东)2020年前三季度,G 省智能机器人产业的总体利润率
(利润率=利润总额/营业收入)约为:
A.-0.6% B.4.6%
C.9.6% D.14.6%
【解析】4.问题时间和材料时间一致,现期时间,问总体利润率→比重,现
期比重问题。利润率=利润总额/营业收入,已知“G省智能机器人产业实现营业
收入326.62亿元”,G省智能机器人产业的利润总额是四大行业的利润总额相加,
四个 数相 加,可 以凑 整两两 相加 , G 省智 能机 器人产 业利 润总额
=-8.61+40.74+0.22+(-0.90)≈32-0.7=31.3,利润率=利润总额/营业收入
=31.3/327,选项差距大,分母截两位,式子变为31.3/33,商快到1,不到1,
首位商9,对应C项。【选C】
特殊题型-饼形图:
题型识别:比重+饼形图
怎么看:12点钟原则(顺时针)
怎么比:排除法
①看内部大小/倍数关系
②找特殊值(1/4,1/2,3/4)
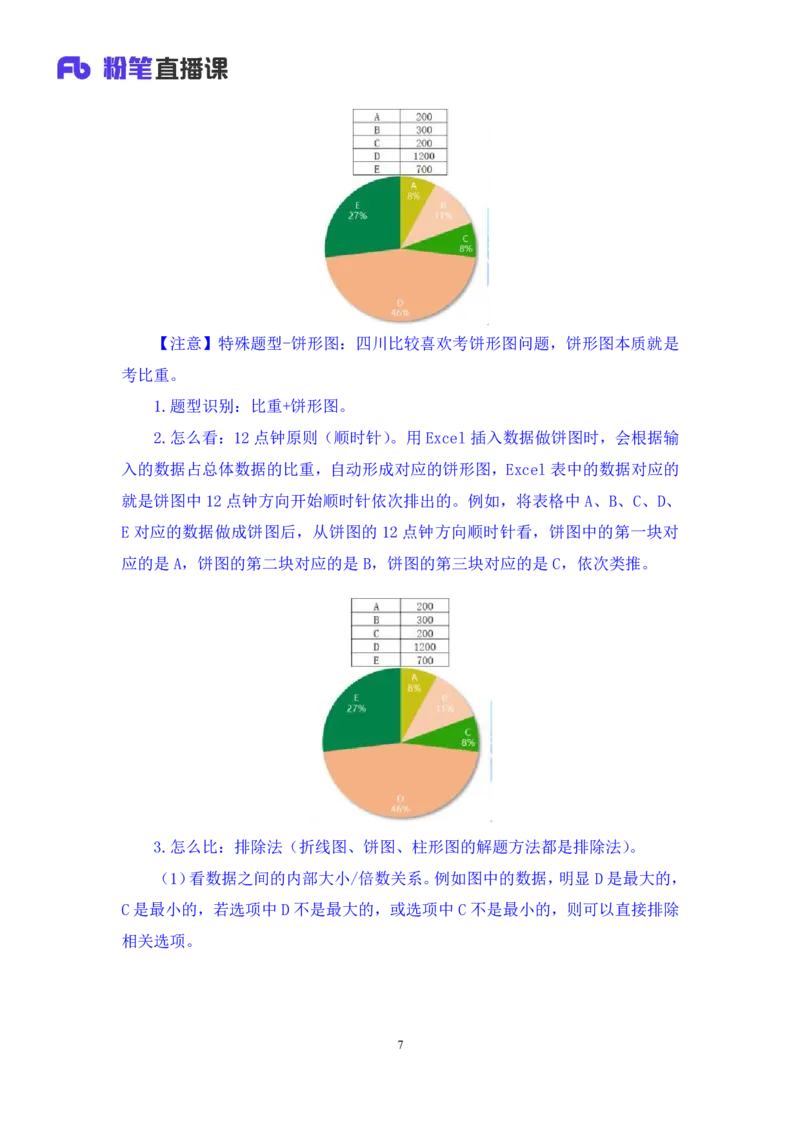
6【注意】特殊题型-饼形图:四川比较喜欢考饼形图问题,饼形图本质就是
考比重。
1.题型识别:比重+饼形图。
2.怎么看:12点钟原则(顺时针)。用Excel插入数据做饼图时,会根据输
入的数据占总体数据的比重,自动形成对应的饼形图,Excel表中的数据对应的
就是饼图中12点钟方向开始顺时针依次排出的。例如,将表格中A、B、C、D、
E 对应的数据做成饼图后,从饼图的 12 点钟方向顺时针看,饼图中的第一块对
应的是A,饼图的第二块对应的是B,饼图的第三块对应的是C,依次类推。
3.怎么比:排除法(折线图、饼图、柱形图的解题方法都是排除法)。
(1)看数据之间的内部大小/倍数关系。例如图中的数据,明显D是最大的,
C是最小的,若选项中D不是最大的,或选项中C不是最小的,则可以直接排除
相关选项。
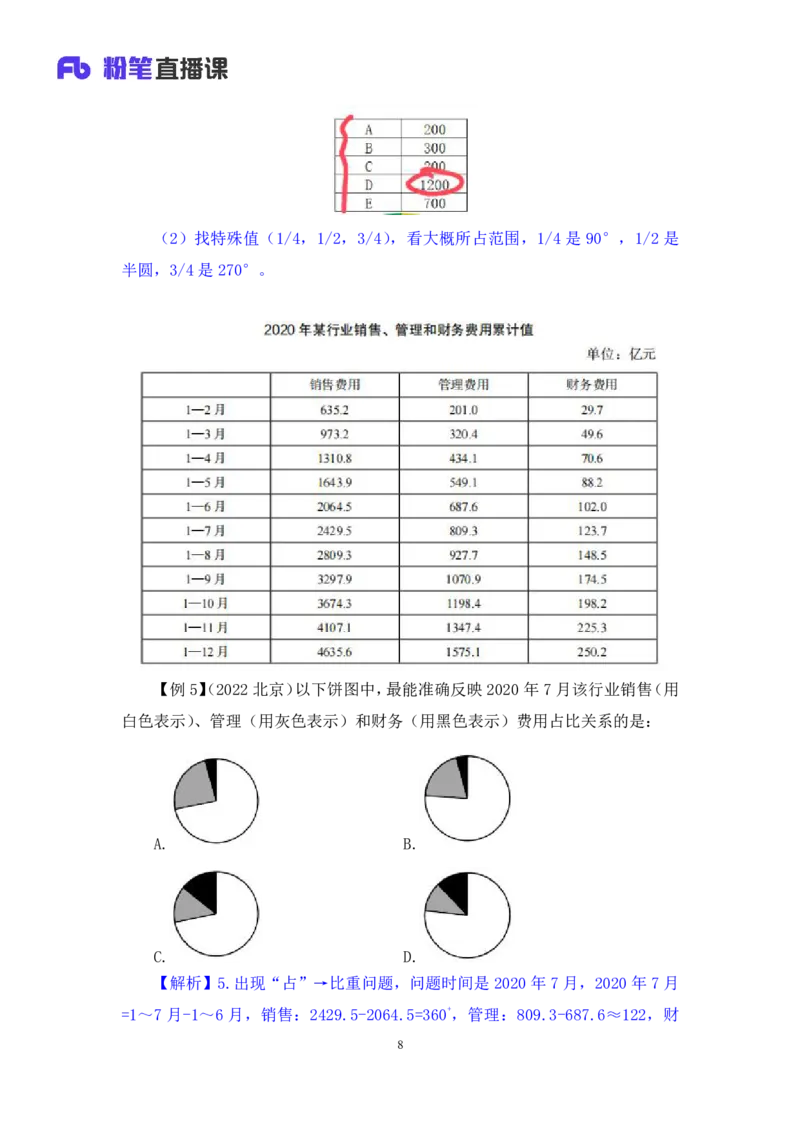
7(2)找特殊值(1/4,1/2,3/4),看大概所占范围,1/4 是 90°,1/2 是
半圆,3/4是270°。
【例5】(2022北京)以下饼图中,最能准确反映2020年7月该行业销售(用
白色表示)、管理(用灰色表示)和财务(用黑色表示)费用占比关系的是:
A. B.
C. D.
【解析】5.出现“占”→比重问题,问题时间是2020年7月,2020年7月
=1~7 月-1~6 月,销售:2429.5-2064.5=360+,管理:809.3-687.6≈122,财
8务:123.7-102≈22。利用最大或最小去排除错误选项,先看最大,最大的是销
售,对应饼图的白色部分,A、B、C、D 项中饼图的白色部分都是最大的,无法
直接排除;再看最小,最小的是财物,对应的是饼图黑色部分,C、D 项中饼图
黑色部分都不是最小的,排除C、D项;
方法一:最后看倍数关系(方法很多、不唯一),销售大约是管理的3倍,B
项中饼图白色部分大约是灰色部分的4倍,A项中饼图白色部分大约是灰色部分
的3倍,排除B项,当选A项。
方法二:若无法直接观察出倍数关系,可以看特殊值。A项饼图白色部分没
有超过270°,B项饼图白色部分超过270°,360/(360+122+22)<3/4,即白
色部分的角度<270°,当选A项。【选A】
二、基期比重
题型识别:问题时间在材料之前,占、比重
计算公式:A/B*(1+b)/(1+a)
A:分子(部分)B:分母(整体)
a:分子的增长率b:分母的增长率
例:2021年点点收入A万,较上年增速为a;全家收入B万,较上年增速为
b。则2020年点点收入占全家的比重为:
【注意】基期比重(重点是速算):
1.题型识别:问题时间在材料之前→基期时间,占→比重,基期比重。
2.计算公式:A/B*(1+b)/(1+a)(1个顶3个,非常重要)。A:分子(部
分),B:分母(整体),a:分子的增长率,b:分母的增长率。
3.例:2021年点点收入A万,较上年增速为a;全家收入B万,较上年增速
为b。则2020年点点收入占全家的比重为?
9答:问去年的时间+占→基期比重,所求=去年我的收入/去年全家的收入,
2020年的基期:我的收入=A/(1+a),全家的收入=B/(1+b),去年我的收入/去
年全家的收入=A/(1+a)÷[B/(1+b)]=A/(1+a)*(1+b)/B=A/B*(1+b)/
(1+a)(若实在无法理解公式推导过程,可以直接记结论)。
列式训练
基期比重公式:A/B*(1+b)/(1+a)
A:分子的现期量(部分)B:分母的现期量(整体)
a:分子的增长率b:分母的增长率
【练习】17 年进口额12万亿(部分量),同比增长 18%,进出口总额 27万
亿(总体量),同比增长14%。求:16年进口占进出口的比重?
A.42.9% B.44.4%
C.46.6% D.48.2%
12/27*(1+14%)/(1+18%)
【注意】列式训练:
1.基期比重公式:A/B*(1+b)/(1+a)。A:分子的现期量(部分),B:分
母的现期量(整体),a:分子的增长率,b:分母的增长率。
2.练习:17 年进口额12万亿(部分量),同比增长 18%,进出口总额 27万
亿(总体量),同比增长14%。求:16年进口占进出口的比重?
A.42.9% B.44.4%
C.46.6% D.48.2%
答:问题时间是 16年,题目时间是 17年,基期时间,“占”→比重,基期
比重问题。基期比重=A/B*(1+b)/(1+a)=12/27*(1+14%)/(1+18%)。多步
除法计算,选项为王,先看选项,若选项差距大,分子、分母截两位,然后约分;
若选项差距小,截三位计算太慢,将式子分成两部分看,先看12/27,进行估算,
再看(1+14%)/(1+18%)与“1”的大小关系。本题选项差距小,12/27=4/9,
1/9≈11.1%,4/9=4*(1/9)≈44.4%,B项是坑,排除;(1+14%)/(1+18%)=1-,
则12/27*(1+14%)/(1+18%)<44.4%,排除C、D项,当选A项。
103.练习(有两个选项<44.4%):17 年进口额 12 万亿(部分量),同比增长
18%,进出口总额 27万亿(总体量),同比增长 14%。求:16年进口占进出口的
比重?
A.42.9% B.44.4%
C.46.6% D.38.2%
答:12/27*(1+14%)/(1+18%),12/27=4/9,1/9≈11.1%,4/9≈44.4%,
选项中有两个选项小于44.4%,(1+14%)/(1+18%)=1.14/1.18=(1.18-0.04)
/1.18=1-0.04/1.18 , 0.04/1.18 ≈ 4% , 原 式 =44.4%* ( 1-0.04/1.18 ) ≈
44.4%-44.4%*0.04≈44.4%-1.6%,比44.4%小一点点,结果为42.X%,不可能在
40%以下,当选A项。
二、基期比重
题型识别:问题时间在材料之前,求比重
公式:
1.给现期和增量:做差求基期(较少)
2.给现期和增速:基期比重=A/B*(1+b)/(1+a)(主流)
速算:
1.选项差距大,上下全部截两位直除(约分);
2.选项差距小,先计算现期比重,再观察(1+b)/(1+a)大于1或小于1,
结合选项排除答案。
Tips:现在出题人往往喜欢给出现期比重,注意利用材料已有数据
【注意】基期比重:
1.题型识别:问题时间在材料之前,求比重。
2.公式:
(1)给现期和增量:做差求基期(较少),(部分的现期-部分的增量)/(总
体的现期-总体的增量)。
(2)给现期和增速:基期比重=A/B*(1+b)/(1+a)(主流)。
3.速算:
(1)选项差距大,上下全部截两位直除(约分)。
11(2)选项差距小,先计算现期比重(A/B),再观察(1+b)/(1+a)大于1
或小于1,结合选项的特点排除答案。
4.Tips:现在出题人往往喜欢给出现期比重→直接用,注意利用材料已有数
据。
基期比重计算练一练
【练习1】57.5%*(1+8.8%)/(1+8.6%)
A.53.6% B.57.6%
C.60.6% D.63.6%
【练习2】20%*(1+7.5%)/(1+9.7%)
A.16.0% B.19.6%
C.22.4% D.25.6%
【练习3】50%*(1+8.6%)/(1+12.5%)
A.低于40% B.40%~50%
C.50%~60% D.高于60%
【注意】基期比重计算练一练:
1.练习1:57.5%*(1+8.8%)/(1+8.6%)。
A.53.6% B.57.6%
C.60.6% D.63.6%
答:题目直接给出了A/B,57.5%是A/B,(1+8.8%)/(1+8.6%)=1.088/1.086=1+,
则57.5%*(1+8.8%)/(1+8.6%)>57.5%,排除A项。1.088/1.086≈1(分子、
分母截三位,式子变为1.09/1.09=1),57.5%*比1大一点点的数,当选B项。
2.练习2:20%*(1+7.5%)/(1+9.7%)。
A.16.0% B.19.6%
C.22.4% D.25.6%
答:(1+7.5%)/(1+9.7%)=1-,20%*(1+7.5%)/(1+9.7%)<20%,排除C、
D项;选项差距大,(1+7.5%)/(1+9.7%)分子、分母截两位,变为11/11,则
20%*(1+7.5%)/(1+9.7%)≈20%,约等于20%,又小于20%,当选B项。
3.练习3:50%*(1+8.6%)/(1+12.5%)。
12A.低于40% B.40%~50%
C.50%~60% D.高于60%
答:(1+8.6%)/(1+12.5%)=1-,50%*(1+8.6%)/(1+12.5%)<50%,排
除C、D项,B项是4开头的数,A项是1或2或3开头的,首位不同,选项差距
大,(1+8.6%)/(1+12.5%)分子、分母截两位,变为11/11,则50%*(1+8.6%)
/(1+12.5%)≈50%,约等于50%,又小于50%,当选B项。
【例1】(2022江苏)2020年江苏省实现以新产业、新业态、新模式为主要
内容的“三新”经济增加值 25177 亿元,比上年增长 5.6%,比全省地区生产总
值的增速快1.5个百分点,占全省地区生产总值的比重为24.5%。全省战略性新
兴产业产值增长11.0%,快于规模以上工业5.5个百分点。其中新能源汽车、数
字创意、新能源和高端装备制造业的产值增速分别为 21.0%、19.8%、15.6%和
15.5%。高技术制造业增加值增长10.3%,占规模以上工业的比重为23.5%,提高
1.7个百分点。高技术服务业营业收入增长14.1%,占规模以上服务业的比重为
37.9%,提高 2.4 个百分点。全省碳纤维增强复合材料、新能源汽车、城市轨道
车辆、集成电路、太阳能电池等新产品的产量分别增长48.9%、42.0%、24.5%、
22.3%和 16.5%。全省现代设施农业占地面积 100.5 万公顷,其中属于战略性新
兴产业的中药材种植业种植面积1.8万公顷,实现产值32亿元,产值增长138.1%。
全省网上零售额10602亿元,增长10.0%。其中,实物商品网上零售额增长 13.9%,
增速比上年快5.2个百分点,占社会消费品零售总额37086亿元的比重为24.9%,
提高2.7个百分点。
2019年江苏省“三新”经济增加值占全省地区生产总值的比重是:
A.20.5% B.24.2%
C.27.1% D.30.0%
【解析】1.问题时间在材料时间之前→基期时间,出现“占”→比重,基期
比重问题,“占”前(“三新”经济增加值)对应部分 A,“占”后(全省地区生
产总值)对应总体B,“三新”经济增加值的增长率→a,全省地区生产总值的增
长率→b,已知“占全省地区生产总值的比重为24.5%”→现期比重(A/B),“比
上年增长5.6%,比全省地区生产总值的增速快1.5个百分点”,给百分数和百分
13点,求百分数,高减低加,“快”用减法,全省地区生产总值的增速(b)
=5.6%-1.5%=4.1%,基期比重=(A/B)*(1+b)/(1+a)=24.5%*(1+4.1%)/(1+5.6%),
选项差距大,(1+4.1%)/(1+5.6%)<1,24.5%*(1+4.1%)/(1+5.6%)<24.5%,
排除C、D项;(1+4.1%)/(1+5.6%)比“1”小一点点,24.5%*比1小一点点的
数,结果比24.5%稍小一点点,当选B项。【选B】
【注意】
1.基期比重=(A/B)*(1+b)/(1+a)=24.5%*(1+4.1%)/(1+5.6%)。
2.A:分子的现期量,B:分母的现期量,a:分子的增长率,b:分母的增长
率。
【例2】(2023联考)2022年,规模以上工业企业中,分行业看:采矿业实
现利润总额15573.6亿元,同比增长48.6%;制造业实现利润总额64150.2亿元,
同比下降 13.4%;电力、热力、燃气及水生产和供应业实现利润总额 4314.7亿
元,同比增长41.8%。
2022年,在41个工业大类行业中,利润总额由高到低的前十个行业的利润
情况如下:煤炭开采和洗选业实现利润总额10202亿元,同比增长44.3%;计算
机、通信和其他电子设备制造业实现利润总额 7389.5 亿元,同比下降 13.1%;
化学原料和化学制品制造业实现利润总额7302.6亿元,同比下降8.7%;电气机
械和器材制造业实现利润总额 5915.6 亿元,同比增长 31.2%;汽车制造业实现
利润总额 5319.6 亿元,同比增长 0.6%;非金属矿物制品业实现利润总额 4759
亿元,同比下降15.5%;医药制造业实现利润总额4288.7亿元,同比下降31.8%;
石油和天然气开采业实现利润总额3545亿元,同比增长109.8%;通用设备制造
业实现利润总额3250.3亿元,同比增长0.4%;电力、热力生产和供应业实现利
润总额3154亿元,同比增长86.3%。
2021年,石油和天然气开采业利润总额占采矿业利润总额的:
A.不足10% B.10%~20%之间
C.20%~30%之间 D.30%以上
14【解析】2.问题时间在材料时间之前,基期时间,“占”→比重,基期比重
问题;“占”前(石油和天然气开采业利润总额)是部分(A),“占”后(采矿业
利润总额)是总体(B)。已知“采矿业实现利润总额 15573.6 亿元,同比增长
48.6%;石油和天然气开采业实现利润总额3545亿元,同比增长109.8%”,基期
比重=(A/B)*(1+b)/(1+a)=3545/15573.6*(1+48.6%)/(1+109.8%),选
项差距大,分子、分母截两位,选项带着范围,截位时带着量级计算,式子变为
3500/16000*1.5/2.1=25/160=10+%,对应B项。【选B】
【注意】
1.基期比重=(A/B)*(1+b)/(1+a)=3545/15573.6*(1+48.6%)/(1+109.8%)。
2.A:分子的现期量,B:分母的现期量,a:分子的增长率,b:分母的增长
率。
3.选项是范围时,优先认为选项差距是比较大的,A项不足10%(可能是7%、
8%、9%等),B项是1X开头的,C项是2X开头的,D项是3X或4X或5X开头的,
类似于首位不一样,因此选项差距是大的。
4.选项差距大,3545/15573.6分子、分母截两位计算,若直接截位为35/16,
假设首位商2,若选择C项,结果不一定正确,因为答案可能是20+%,也有可能
是2+%,无法确定正确答案是哪一个,因此当选项是范围时,截位时要带着量级
计算。
三、两期比重
两期比重之升降判断
题型识别:两个时间+比重+上升/下降
计算公式:现期比- 基期比=A/B-(A/B)*(1+b)/(1+a)=(A/B)*(a-b)
/(1+a)。
升降判断:a>b,比重上升
a<b,比重下降
a=b,比重不变
a:分子的增长率,b:分母的增长率
15注:比较时带正负号进行比较
【注意】两期比重之升降判断:
1.题型识别:两个时间+比重+上升/下降。例如,今年我占全家工资的比重
比去年上升/下降。
2.计算公式:现期比- 基期比=A/B-(A/B)*(1+b)/(1+a)=(A/B)*(a-b)
/(1+a),公式的本质是比重的增长量(比重差、比重的变化量)。
(1)现期比(今年的比重)- 基期比(去年的比重),若现期比- 基期比>
0,说明今年的比重比去年大;若现期比- 基期比<0,说明今年的比重比去年小。
(2)现期比- 基期比=A/B-(A/B)*(1+b)/(1+a)=(A/B)*[1-(1+b)
/(1+a)]=(A/B)*[(1+a-1-b)/(1+a)]=(A/B)*(a-b)/(1+a)。现期比
- 基期比>0,比重上升;现期比- 基期比<0,比重下降。
3.升降判断:A/B一定是一个小于等于 1 的正数,a可能是负的,但 a一定
>-100%,则 1+a 一定是正数,因此(A/B)*(a-b)/(1+a)的正负是由 a-b
决定的,若 a-b>0,则(A/B)*(a-b)/(1+a)>0,比重上升;若 a-b<0,
则(A/B)*(a-b)/(1+a)<0,比重下降。
(1)a>b,比重上升。
(2)a<b,比重下降。
(3)a=b,比重不变。
(4)a:分子的增长率,b:分母的增长率。
(5)注:比较时带正负号进行比较。
两期比重升降判断练习:
a>b,比重上升;
a<b,比重下降;
a=b,比重不变。
示例:2022年总收入10万元,同比增长10%,2022年工资收入8万,同比
增长5%。
判断:2022年工资收入占总收入的比重比上年上升还是下降?
16【注意】两期比重升降判断练习:
1.a>b,比重上升;a<b,比重下降;a=b,比重不变。
2.示例:2022年总收入10万元,同比增长10%,2022年工资收入8万,同
比增长5%。判断:2022年工资收入占总收入的比重比上年上升还是下降?
答:a=5%,b=10%,a<b,比重下降。
3.a=5%,b=10%,a<b,比重下降;a=10%,b=-5%,a>b,比重上升;a=-10%,
b=10%,a<b,比重下降;a=-10%,b=-5%,a<b,比重下降;a=-15%,b=-35%,
a>b,比重上升。
据对全国 6.4 万家规模以上文化及相关产业企业调查,2021 年前三季度,
上述企业实现营业收入84205亿元,按可比口径计算,同比增长21.8%;两年平
均增长10.0%。
分行业类别营业收入情况:新闻信息服务 9847 亿元,同比增长 22.1%;内
容创作生产17693亿元,同比增长18.6%;创意设计服务13787亿元,同比增长
24.0%;文化传播渠道9309亿元,同比增长30.1%;文化投资运营359亿元,同
比增长 13.8%;文化娱乐休闲服务 916亿元,同比增长 35.3%;文化辅助生产和
17中介服务11441亿元,同比增长18.3%;文化装备生产4880亿元,同比增长17.8%;
文化消费终端生产15974亿元,同比增长22.0%。
【例1】(2023联考)与上一年相比,2021年前三季度分行业类别中,占全
国6.4万家规模以上文化及相关产业企业营业总收入比重增加的行业个数是:
A.3个 B.4个
C.5个 D.6个
【解析】1.2021 年前三季度与上一年相比(两个时间)+占(比重)+增加
→两期比重比较。问比重增加,即a>b。各个行业的增长率对应a,全国6.4万
家规模以上文化及相关产业企业的增长率对应 b,定位材料找数据,b=21.8%;
新闻信息服务:a=22.1%>b=21.8%,满足;内容创作生产:a=18.6%<b=21.8%,
不满足;创意设计服务:a=24.0%>b=21.8%,满足;文化传播渠道:a=30.1%>
b=21.8%,满足;文化投资运营:a=13.8%<b=21.8%,不满足;文化娱乐休闲服
务:a=35.3%>b=21.8%,满足;文化辅助生产和中介服务:a=18.3%<b=21.8%,
不满足;文化装备生产:a=17.8%<b=21.8%,不满足;文化消费终端生产:a=22.0%
>b=21.8%,满足。满足a>b的一共有5个,对应C项。【选C】
【例 2】(2021 四川)2019 年,我国电信业务收入完成 1.31 万亿元,比上
年增长0.8%。其中:固定数据及互联网业务收入完成2175亿元,比上年增长5.1%;
移动数据及互联网业务收入6082亿元,比上年增长1.5%;固定增值业务收入1371
亿元,比上年增长21.2%,其中,IPTV(网络电视)业务收入294亿元,比上年
增长21.1%;物联网业务收入比上年增长25.5%。
下列指标中,2019年的数值高于2018年的有几项?
①固定数据及互联网业务收入占电信业务收入比重
②移动数据及互联网业务收入占电信业务收入比重
③IPTV业务收入占固定增值业务收入比重
A.0 B.1
C.2 D.3
【解析】2.问题有两个时间+占+高于→两期比重比较问题,问“2019 年的
数值高于2018年”,即a>b。“占”前的增长率对应a,“占”后的增长率对应b。
18已知“2019年,我国电信业务收入比上年增长 0.8%。其中:固定数据及互联网
业务比上年增长5.1%;固定增值业务比上年增长21.2%,其中,IPTV(网络电视)
业务比上年增长 21.1%”,①:a=5.1%>b=0.8%,满足;②:a=1.5%>b=0.8%,
满足;③:a=21.1%<b=21.2%,不满足。满足 a>b 的一共有两个,对应 C 项。
【选C】
三、两期比重之计算
题型识别:两个时间+比重+上升/下降+几个百分点
真题1:2017年5月,股份制商业银行总资产占银行业金融机构的比重与上
年相比约:
A.增加了2个百分点 B.减少了2个百分点
C.增加了0.2个百分点 D.减少了0.2个百分点
真题2:2017年J省海洋生产总值占全国的比重同比:
A.上升了约0.2个百分点 B.上升了约2个百分点
C.下降了约0.2个百分点 D.下降了约2个百分点
计算技巧:A/B-A/B*[(1+b)/(1+a)]=A/B*[(a-b)/(1+a)]=A/B*[1/
(1+a)]*(a-b)
当a>0时,A/B<1,1/(1+a)<1,即结果<|a-b|
当a<0时,A/B<1,1/(1+a)>1,大小结果不确定,但真题中绝大多数
都<|a-b|
结论:在实际做题过程中,两期比重差绝大多数都<|a-b|
解题步骤:
1.判方向:a>b,上升;a<b,下降
2.定大小:小于|a-b|
注:
1.若选项中只有一个小于|a-b|,直接选即可
2.若选项中有多个小于|a-b|,代入公式截位估算。
【注意】两期比重之计算:两期比重的知识点(比较、计算)之间是递进关
系,浅层次→今年比重比去年比重上升/下降,进一步追问→今年比重比去年比
19重上升/下降多少→计算。比重上升多少,结合常识,比重本身就是“%”,统计
学中,不会列“(现期%- 基期%)/基期%”这样的式子,不符合实际,资料分析
的数据都是官方统计局公布的真实数据→符合统计学的基本原理,故不会这样计
算;看到百分点,可以加减,就比重而言,计算“现期%- 基期%=比重的增长量”,
不能计算比重的增长率;比重的单位是“%”,做减法之后利用“百分点”进行表
示,即两期比重计算只能做减法。
1.题型识别:两个时间+比重+上升/下降+几个百分点。
2.真题1:2017年5月,股份制商业银行总资产占银行业金融机构的比重与
上年相比约:
A.增加了2个百分点 B.减少了2个百分点
C.增加了0.2个百分点 D.减少了0.2个百分点
答:两个时间(2017 年 5 月、上年→2016 年 5 月)+比重(“占”)+增加/
减少+百分点,两期比重计算问题,计算比重的增长量。
3.真题2:2017年J省海洋生产总值占全国的比重同比:
A.上升了约0.2个百分点 B.上升了约2个百分点
C.下降了约0.2个百分点 D.下降了约2个百分点
答:两个时间(2017年、同比→与去年同期相比→2016年)+比重(“占”)
+上升/下降+百分点,两期比重计算问题,计算比重的增长量。
4.计算技巧:比重的增长量(比重的差值)=现期比重- 基期比重
=A/B-A/B*[(1+b)/(1+a)]=A/B*[(a-b)/(1+a)]=A/B*[1/(1+a)]*(a-b)。
(1)当 a>0时,A/B<1,1/(1+a)<1,即结果<|a-b|。之所以加绝对
值,因为有时“a-b”为负数,负数代表下降,下降多少需要看绝对值。
(2)当a<0时,A/B<1,1/(1+a)>1,大小结果不确定;结合经验,真
题中绝大多数(99%的题目)都<|a-b|,只有广东出现过1个反例。
5.结论:在实际做题过程中,两期比重差绝大多数都<|a-b|。如果怀疑结
论,则只能代入公式“A/B*[(a-b)/(1+a)]”计算,选项差距大→截两位、
选项差距小→截三位或者先算“A/B”。
6.解题步骤:
(1)判方向(基本上可以排除2个错误选项):a>b,上升;a<b,下降。
20(2)定大小:小于|a-b|。
7.注:
(1)若选项中只有一个小于|a-b|,直接选即可(秒杀题)。
(2)若选项中有多个小于|a-b|→定大小排除不了错误选项,代入公式截位
估算(真题中,目前都是选项差距大,截两位估算即可,选项为王)。
五年来,我国积极推进网络强国和数字中国建设,着力深化数字经济与实体
经济融合,为打造数字经济新优势、增强经济发展新动能提供有力支撑。2022
年,我国电信业务收入累计完成 1.58 万亿元,比上年增长 8%,较 2018 年增长
超2800亿元。
2022年移动数据流量业务收入6397亿元,比上年增长0.3%,在电信业务收
入中占比约为40.5%。数据中心、云计算、大数据、物联网等新兴业务快速发展,
对我国电信业务拉动作用持续增强。2022年新兴业务收入达3072亿元,在电信
业务收入中占比由上年的 16.1%提升至 19.4%。其中,数据中心、云计算、大数
据、物联网业务比上年分别增长11.5%、118.2%、58.0%和24.7%。
【例 3】(2023 广东)与 2021 年相比,2022 年我国移动数据流量业务收入
在电信业务收入中的占比:
A.增加了约3个百分点 B.减少了约3个百分点
C.增加了约13个百分点 D.减少了约13个百分点
【解析】3.两个时间(2021年、2022年)+比重(在……中的占比)+增加/
减少+百分点,两期比重计算问题。判升降:“占”前是部分→移动数据流量业务
收入的增长率对应a、“占”后是总体→电信业务收入的增长率对应b,定位材料
找数据,a=0.3%<b=8%→下降(“减少”),排除 A、C 项。定大小:<
|a-b|=|0.3%-8%|=7.7个百分点,对应B项。【选B】
2020 年,C 市天然气用量为 107.47 亿立方米,同比增长 3.83%。其中,中
石油供应73.96亿立方米,同比增长1.72%;中石化供应33.51亿立方米,同比
增长 8.8%。从用气结构看:民用气为 33.75 亿立方米,同比增长 5.4%;CNG 用
气6.99亿立方米,同比下降13.92%;工业用气66.73亿立方米,同比增长5.3%。
21【例4】(2022国考)2020年,中石化供气量占C市天然气用量的比重比上
年:
A.减少了不到3个百分点 B.增加了不到3个百分点
C.减少了3个百分点以上 D.增加了3个百分点以上
【解析】4.两个时间(2020年、上年→2019年)+比重(“占”)+增加/减少
+百分点,两期比重计算问题。判升降:“占”前是部分→中石化供气量的增长率
对应a、“占”后是总体→C市天然气用量的增长率对应b,定位材料找数据,a=8.8%
>b=3.83%→上升,排除A、C项。定大小:<|a-b|=|8.8%-3.83%|≈5个百分点,
B、D项均可能是答案。代入公式“A/B*[(a-b)/(1+a)]”:不要抄原始数据,
结合选项,判断结果与“3个百分点”的大小关系即可;A/B=33.51/107.47≈0.3,
选项差距大→截两位,即0.3*(5个百分点/1.1)=(1.5/1.1)个百分点<3个
百分点,对应B项。【选B】
【注意】如果没时间,可以猜最小,能够保证80%的正确率;但是,国考、
山东出现过反例,近两年不推荐猜最小。
【注意】比重:
1.现期比重:考查最多,非常简单。
2.基期比重:记住公式“A/B*[(1+b)/(1+a)]”,课下多练习速算。
3.两期比重:
(1)结论:升降判断→比较部分和整体增长率,a>b→上升、a<b→下降。
22(2)技巧——计算两期比重差值(两期比重的增长量):80%的题目不用公
式“A/B*[(a-b)/(1+a)]”,大多数的题目→判升降、定大小(<|a-b|);如
果无法确定答案,现阶段建议练习速算,猜最小是下下策。
第六节 平均数
关键字:均、每、单位面积、单价
题型:
一、现期平均数
二、基期平均数
三、两期平均数
【注意】平均数问题:建立在比重知识的背景下进行学习,则没有那么复杂。
1.关键字(表达“平均”的含义):均、每、单位面积、单价。
2.题型:根据时间的不同进行划分。
(1)现期平均数。
(2)基期平均数。
(3)两期平均数。
一、现期平均数
题型识别:问题时间与材料一致+平均(均/每/单位面积/单价)
计算公式:
1.多个数的平均值(总和/个数)
2.后/前
(1)人均收入=收入/人数
(2)单位面积产量=产量/面积
(3)平均单价=总金额/货物量
速算技巧:截位直除
【注意】现期平均数:
1.题型识别:问题时间与材料一致+平均(均/每/单位面积/单价)。
2.计算公式:
23(1)多个数的平均值(总和/个数)。例:求10位同学的平均分,所求=10
位同学的分数加和/10。
(2)后/前(难点):可以解决90+%的平均数涉及的分子、分母问题。
①人均收入=收入(后)/人数(前)。
②单位面积产量=产量(后)/面积(前)。
③平均单价=总金额(后)/货物量(前)。
3.速算技巧:除法→截位直除。
4.平均数=A/B,A对应后面的主体(增长率为a)、B对应前面的主体(增长
率为b);区分:比重=部分(A)/总体(B)。
2021 年 H 省共有电子商务平台 87 个,在本省电商平台上实现交易金额为
5354.93亿元,同比增长41.0%,收取的平台交易服务费为3.17亿元,同比增长
49.5%。从地区分布来看,2021年本地电子商务平台拥有量最多的为Z市,有44
个平台,实现交易金额4239.04亿元。
【例1】(2023国考)2021年,H 省除Z市外其他地区的电子商务平台平均
每个平台实现的交易金额约为多少亿元?
A.5 B.12
C.26 D.62
【解析】1.问题时间是2021 年,为现期时间;出现“平均每”,现期平均数
问题;重点→找分子、分母,平均数=后/前→平均每个平台的金额=金额/平台。
不要利用“2021年H省共有电子商务平台87个,在本省电商平台上实现交易金
额为5354.93亿元”,否则会掉主体坑;主体为“除Z市外”,所求≈(53|54-42|39)
/(87-44);计算之前看选项,选项差距大,截两位→原式转化为 11XX/43,首
位商2,对应C项。【选C】
2021年上半年,湖北省676家规上信息软件业企业中营业收入前20的企业
共实现营业收入355.46亿元,同比增长8.3%,拉动规上服务业营业收入增长1.1
个百分点。
【例2】(2022湖北选调)2021年上半年湖北省规上信息软件业中营业收入
24前20的企业,平均每家每月营业收入约为多少亿元?
A.1.18 B.2.25
C.2.32 D.2.96
【解析】2.问题时间是2021年上半年,为现期时间;出现“平均每家每月”,
现期平均数问题;出现2个“每”→需要除以2次,平均数=后/前=收入/(家数
*月份数)。主体为“湖北省规上信息软件业中营业收入前20的企业”,上半年对
应6个月,所求≈355/(20*6)=355/120=3-(约等于3),对应D项。【选D】
二、基期平均数
题型识别:问题时间在材料时间之前+平均(均、每、单位)
基期平均数=A/B*[(1+b)/(1+a)],常考;(A-A的增长量)/(B-B的增
长量),少考。
A:总数现期量;B:个数现期量;a:总数增长率;b:个数增长率
【例】2022年棉花产量A,较上年增速为a,种植面积为B亩,较上年增速
为b。问:2021年棉花平均每亩产量?
速算:分析选项差距(同基期比重)
①差距大,截两位直除,约分计算
②差距小,算“前”看“后”,计算A/B且结合(1+b)/(1+a)与1的大小
关系
【注意】基期平均数:
1.题型识别:问题时间在材料时间之前+平均(均、每、单位)。
2.公式:A/B*[(1+b)/(1+a)]→与基期比重的公式、推导过程一模一样,
常考;(A-A的增长量)/(B-B的增长量),少考。
3.A:总数现期量;B:个数现期量;a:总数增长率;b:个数增长率。
4.例:2022年棉花产量A,较上年增速为a,种植面积为B亩,较上年增速
为b。问:2021年棉花平均每亩产量?
答:问题时间是2021年,为基期时间;出现“平均每”,基期平均数问题;
平均数=后/前→平均每亩产量=产量/亩数,产量对应 A、亩数对应 B,套公式
“A/B*[(1+b)/(1+a)]”求解。
255.速算:分析选项差距(同基期比重,选项为王)。
(1)差距大,截两位直除,约分计算;不能约分,可以微调“1”。
(2)差距小,算“前”看“后”,计算 A/B且结合(1+b)/(1+a)与1 的
大小关系。假设b=-5%,则为1+(-5%)=1-5%。
6.拓展:2022年棉花产量A,比去年多5吨,种植面积为B亩,比去年多3
亩。问:2021年棉花平均每亩产量?
答:平均数=后/前→平均每亩产量=产量/亩数,所求=(A-A的增长量)/(B-B
的增长量)=(A-5)/(B-3)。
2017年全国共有各级各类民办学校17.76万所,占全国学校总数的34.57%;
各类民办教育在校生达5120.47万人,比上年增长6.12%。其中:民办幼儿园16.04
万所,比上年增长 4.00%;在园儿童 2572.34 万人,比上年增长 5.53%。民办普
通小学 6107 所,比上年增长 2.21%;在校生 814.17万人,比上年增长 7.65%。
民办初中5277所,比上年增长3.78%;在校生577.68万人,比上年增长8.42%。
民办普通高中3002所,比上年增长7.71%;在校生306.26万人,比上年增长9.74%。
民办中等职业学校2069所,比上年下降2.17%;在校生197.33万人,比上年增
长7.16%。
【例3】(2020北京)2016年平均每所民办中等职业学校在校生人数约为:
A.871人 B.991人
C.1091人 D.1181人
【解析】3.材料时间是2017 年,问题时间是2016年,为基期;出现“平均
每”,基期平均数问题;主体为“中等职业学校”,材料给出现期量和增长率,利
用公式“A/B*[(1+b)/(1+a)]”求解。平均数=后/前=在校生人数(A、a)/
学校数(B、b),所求=197.33/2069*[(1-2.17%)/(1+7.16%)]。计算之前先
看选项,C、D项首位相同,次位差=首位,选项差距小;先算 A/B,可以截三位
列“厂”除→19733/207,但是没必要,尝试估算范围,选项之间没有10倍、100
倍的差别,不管小数点、直接看有效数字→197/2=98.5(有效数字为 985),则
197.33/2069的有效数字为985-;再看“(1+b)/(1+a)”与1的关系,(1-2.17%)
/(1+7.16%)的分子小、分母大→(1-2.17%)/(1+7.16%)<1;原式转化为
26985-*1-<985,对应A项。【选A】
2017 年,S 市服务业小微样本企业总体应付职工薪酬 19.28 亿元,比 2016
年增长 9.3%。户均应付职工薪酬 93.50 万元。从业人员人数 29028 人,人均年
薪酬6.64万元,比2016年增加0.60万元。
【例4】(2020四川)S市服务业小微样本企业2016年从业人员总数最接近
以下哪个数字?
A.26565 B.27001
C.29205 D.35015
【解析】4.问题时间是2016 年,为基期;题干中没有出现“平均每”,从表
面看不是平均数问题;定位材料找数据,已知“(2017年)从业人员人数29028
人”,无法直接求解。“人均年薪酬 6.64 万元,比 2016 年增加 0.60万元”→已
知平均数、求人数,人均年薪=后/前=总薪酬/人数→2016年人数=2016年总薪酬
/2016年人均年薪,基期=现期/(1+r)→2016年总薪酬=19.28/(1+9.3%)、基
期=现期-增长量→2016 年人均年薪=6.64-0.60,所求=19.28/(1+9.3%)÷
(6.64-0.60)。选项没有 10 倍、100 倍的差别,不用管单位、量级;选项差距
小,截三位计算,不用管小数点,原式转化为193/(109*604);乘法估算→193/
(11*6)=193/66,首位商2、次位商9,对应C项。【选C】
【注意】
1.举例理解:A=B/C,求C→C=B/A;假设20=80/x,则x=80/20。
2.本题涉及多个公式,属于双考点,要求融会贯通。
3.关于A*B,A变大一点→变成1.1*A,为了使误差尽量小,A往上加10%,
则B往下压10%→B变成0.9*B,原式转化为1.1*A*(0.9*B)=0.99*A*B。综上,
乘法(A*B)估算中,如果A变大,则B相应变小,可以中和误差。
三、两期平均数之升降判断(与两期比重升降方法相同)
题型识别:题干中涉及两个时间+平均数问法
升降判断:
27a>b,平均数上升;
a<b,平均数下降;
a=b,平均数不变。
a:分子的增长率;b:分母的增长率
【注意】两期平均数之升降判断(与两期比重升降方法、推导过程相同):
比如问“粉笔教师的人均工资比去年上升/下降”,两期平均数的问法;常出现在
综合分析题的某个选项中,单题很少,而两期比重问题单题很多。
1.题型识别:题干中涉及两个时间+平均数问法。
2.升降判断:
(1)a>b,平均数上升。
(2)a<b,平均数下降。
(3)a=b,平均数不变。
3.a:分子的增长率;b:分母的增长率。
2021年上半年,我国进口集成电路3123亿块,同比增长28.4%;进口额1979
亿美元,增长28.3%。出口集成电路1514亿块,增长34.5%;出口额664亿美元,
增长32.0%。
【例1】(2022江苏)能够从上述资料中推出的是:
A.略
B.略
C.2021年上半年,我国集成电路出口平均价格同比有所提高
D.略
【解析】1.综合分析题,先挑好算的选项,两期平均数比较、两期比重比较
找数即可→优先看;A、B、D项与两期平均数比较无关,现阶段不进行讲解。
C项:两个时间(2021年上半年、同比→与去年同期相比)+平均数(“平均
价格”)+提高(a>b),两期平均数比较问题;平均价格=后/前=价钱(a)/量(b),
a=32%<b=34.5%,说法错误。【不选】
2017年,S市服务业小微样本企业总体实现营业收入 105.39 亿元,同比增
28长3.1%,比2016年回落了15.7个百分点,户均实现营业收入510.63万元。
2017年,S市服务业小微样本企业总体营业税金及附加为 1.09亿元,同比
下降 29.5%;缴纳增值税 2.30 亿元,同比增长 11.6%,户均缴纳增值税 11.16
万元。
【例2】(2020四川)能够从上述资料中推出的是:
A.略
B.略
C.略
D.2017年,S市服务业小微样本企业平均每万元营业收入缴纳营业税金及附
加高于上年水平
【解析】2.现阶段只看D项。
D项:两个时间(2017 年、上年)+平均数(平均每万元营业收入缴纳营业
税金及附加)+高于,两期平均数比较问题,“高于”→a>b。不用管陌生的概念,
本题不是计算→不用管单位(“万元”);平均数=后/前=税金(a)/收入(b),定
位材料找数据,a=-29.5%、b=3.1%,a<b→平均数下降,错误。【不选】
三、两期平均数之计算——增长率(平均数的增长率)
识别:平均/每/单位+增长了%
公式:r=(a-b)/(1+b),a是分子的增长率、b是分母的增长率
做题逻辑
①确定分子、分母(谁除以谁)
②代入公式:r=(a-b)/(1+b)
【注意】两期平均数之计算——增长率(平均数的增长率):
1.识别:平均/每/单位+增长了%(增长率问法),本质是增长率。
2.公式:r=(a-b)/(1+b),纯口算,a 是分子的增长率、b是分母的增长
率。推导:r=现期/基期-1=A/B÷{A/B*[(1+b)/(1+a)]}-1=1÷[(1+b)/(1+a)]-1=
(1+a)/(1+b)-1=(1+a)/(1+b)-(1+b)/(1+b)=(1+a-1-b)/(1+b)=
(a-b)/(1+b),平均数的增长率只跟a、b有关,与A、B无关(推导的过程中
被约掉了)。
293.做题逻辑:
(1)确定分子、分母(谁除以谁)。
(2)代入公式:r=(a-b)/(1+b)。
4.平均数——两种问法:假设今年的人均工资为100元、去年的人均工资为
80元,第一种问法→人均工资的增长率(r)=(100-80)/80,第二种问法→人
均工资增长了多少元(增长量)=100-80。
2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%,增速
比上半年放缓0.7个百分点。其中,工业品物流总额16636.15亿元,同比增长
0.2%,增速比上半年放缓 2.1 个百分点;外部流入(含进口)货物物流总额
17357.31亿元,同比增长12.1%,增速比上半年加快0.8个百分点;农产品物流
总额 875.06 亿元,同比增长 11.6%,增速比上半年加快 0.5 个百分点;单位与
居民物品物流总额 457.86 亿元,同比增长 40.7%,增速比上半年放缓 3 个百分
点;再生资源物流总额 30.88 亿元,同比下降 7.0%,降幅比上半年扩大 4.3 个
百分点。
2018年前三季度,S省社会物流总费用2682.1亿元,同比增长6.3%,比上
半年放缓0.9个百分点。其中:物流运输环节总费用1854.6亿元,同比增长6.3%;
保管环节总费用 612.4 亿元,同比增长 6.4%;管理环节总费用 214.9 亿元,同
比增长6.4%。
【例3】(2020国考)2018年前三季度,平均每万元社会物流总额产生的物
流费用比上年同期:
A.上升了不到1% B.上升了1%以上
C.下降了不到1% D.下降了1%以上
【解析】3.看选项→上升/下降+%,增长率问题;主体是“平均……”,平均
数的增长率问题,公式:r=(a-b)/(1+b)。平均数=后/前=费用(a)/总额(b),
所求=(6.3%-6.4%)/(1+6.4%)=-0.1%/1+,下降了不到0.1%;结合选项,下降
了不到1%,对应C项。【选C】
【注意】这种题没有计算量,重点考查“识别+找分子、分母”。
30知识拓展:两期平均数之计算——增长量(平均数的增长量)
识别:平均/每/单位+增长+具体单位
公式:现期平均数- 基期平均数=A/B-A/B*[(1+b)/(1+a)]=A/B*[(a-b)
/(1+a)]
速算:结合选项截位直除
【注意】知识拓展:两期平均数之计算——增长量(平均数的增长量),四
川会考。比如问“人均工资增长了多少元”,增长+具体单位→增长量,主体为“人
均工资”,考查平均数的增长量。
1.识别:平均/每/单位+增长+具体单位。
2.公式:增长量=现期- 基期→平均数的增长量=现期平均数- 基期平均数
=A/B-A/B*[(1+b)/(1+a)]=A/B*[(a-b)/(1+a)],与比重的增长量一样;
比重→%-%=百分点,平均数→多少元-多少元=多少元,二者的单位不一样、外观
一样。
3.速算:多步除法→结合选项截位直除,无特定技巧(原因:“A/B”不一定
小于1)。
4.解释:平均数中,平均数=后(A)/前(B)。
2020年,全国艺术表演团体共演出 225.61万场,比上年下降 24.0%;国内
观众8.93亿人次,下降27.4%;演出收入86.63亿元,下降31.7%。
【拓展】(2022四川)2020年,全国艺术表演团体平均每场演出创造收入比
上年:
A.减少了不到1000元 B.减少了1000元以上
C.增加了不到1000元 D.增加了1000元以上
【解析】拓展.看选项,增加/减少+具体单位→增长量的问法;主体是“平
均……”,考查平均数的增长量;公式:A/B*[(a-b)/(1+a)],平均数=后/
前=收入(A、a)/演出场次(B、b)。定位材料找数据,所求=86.63 亿/225.61
万*[(-31.7%+24%)/(1-31.7%)];选项是范围,优先认为选项差距大,可以
截两位;假设约分之后的结果为2,2000→1000元以上、200→不到1000元,则
31需要管单位。原式的结果为负→减少,排除C、D项;截两位→87万/230*(-8/68),
结合选项→与1000进行比较,转化为870*1000/230*(-1/8)=1000*(87/23)
*(-1/8)=1000*(-1-)=-1000-,即减少了不到1000元,对应A项。【选A】
【注意】平均数:
1.搞清楚分子、分母,平均数=后(A)/前(B)。
2.基期平均数(与基期比重公式一样):A/B*[(1+b)/(1+a)]。
3.两期平均数:
(1)升降判断:与两期比重一样。
(2)计算:
①平均数的增长量(与比重一样):A/B*[(a-b)/(1+a)]。
②平均数的增长率=(a-b)/(1+b)。
32【注意】比重、平均数考点辨析:二者的外观一样。
1.比重只计算差值、不计算“率”:两期比重差=A/B*[(a-b)/(1+a)]。
2.平均数既要计算差值、又要计算增长率:平均数的差(平均数的增长量)
=A/B*[(a-b)/(1+a)],平均数的增长率=(a-b)/(1+b)。
3.比重=部分(A)/总体(B)<1,平均数(重点看位置)=后(A)/前(B)。
4.比重、平均数:基期、升降判断一样。
【注意】知识梳理:
1.比重,部分在总体中所占的比率;平均数,看位置→后除以前。
2.现期比重公式:A/B=部分/总体;现期平均数公式:A/B=后/前。
3.基期比重公式:A/B*[(1+b)/(1+a)];基期平均数公式:A/B*[(1+b)
/(1+a)]。若选项差距大,截两位;若选项差距小,先算 A/B、再看(1+b)/
(1+a)与1的关系。
334.两期比重题型识别:有两个时间,问题中有“占”;两期平均题型识别:
有两个时间,问题中有“均、每、单位”。
5.两期比重判升降:a>b,比重上升;a<b,比重下降;a=b,比重不变。
6.两期平均数判升降:a>b,平均数上升;a<b,平均数下降;a=b,平均
数不变。
7.两期比重差值题型识别:比重+上升/下降+百分点;方法及公式:本质是
增长量→A/B*[(a-b)/(1+a)],第一步→判升降、第二步→定大小。
8.平均数增长率题型识别:平均数+增长/下降+%;公式:r=(a-b)/(1+b)。
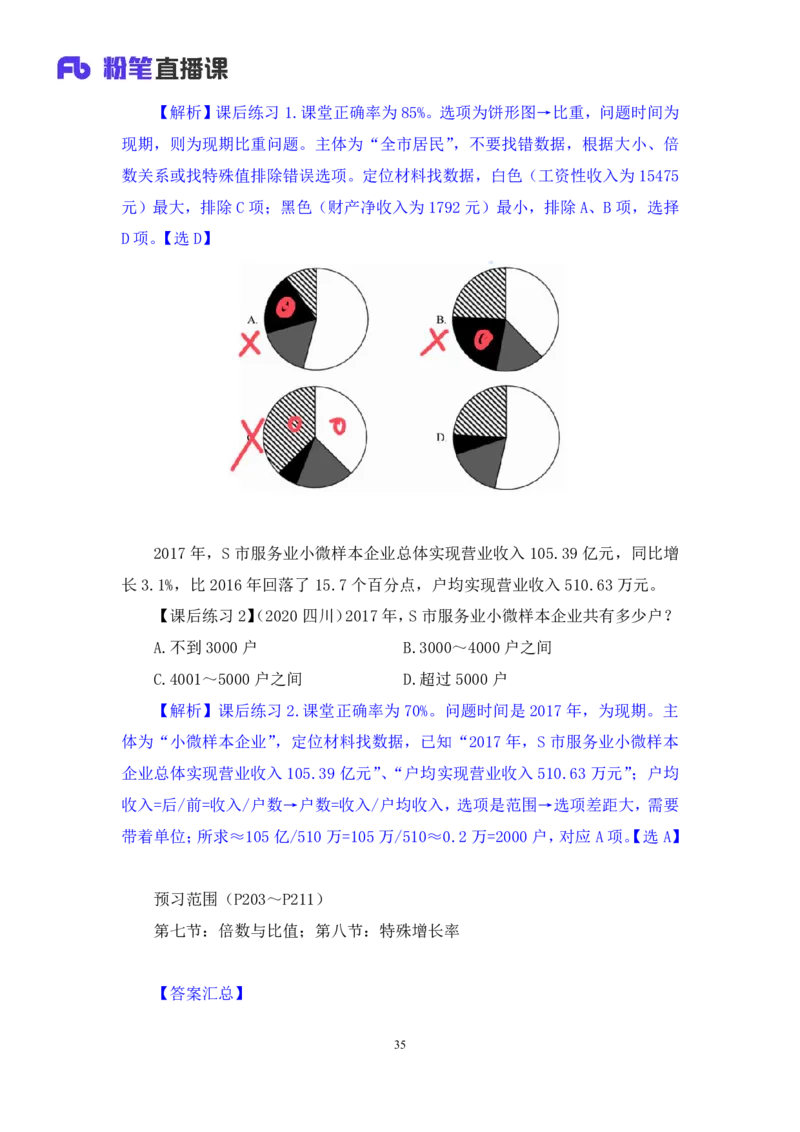
【课后练习1】(2022四川下)以下饼图中,最能准确反映2019年A市全市
居民工资性收入(白色)、经营净收入(灰色)、财产净收入(黑色)和转移净收
入(斜线)占可支配收入比重关系的是:
A. B.
C. D.
34【解析】课后练习1.课堂正确率为85%。选项为饼形图→比重,问题时间为
现期,则为现期比重问题。主体为“全市居民”,不要找错数据,根据大小、倍
数关系或找特殊值排除错误选项。定位材料找数据,白色(工资性收入为 15475
元)最大,排除C项;黑色(财产净收入为1792元)最小,排除A、B项,选择
D项。【选D】
2017年,S市服务业小微样本企业总体实现营业收入 105.39 亿元,同比增
长3.1%,比2016年回落了15.7个百分点,户均实现营业收入510.63万元。
【课后练习2】(2020四川)2017年,S市服务业小微样本企业共有多少户?
A.不到3000户 B.3000~4000户之间
C.4001~5000户之间 D.超过5000户
【解析】课后练习 2.课堂正确率为 70%。问题时间是2017年,为现期。主
体为“小微样本企业”,定位材料找数据,已知“2017年,S市服务业小微样本
企业总体实现营业收入 105.39 亿元”、“户均实现营业收入 510.63 万元”;户均
收入=后/前=收入/户数→户数=收入/户均收入,选项是范围→选项差距大,需要
带着单位;所求≈105亿/510万=105万/510≈0.2万=2000户,对应A项。【选A】
预习范围(P203~P211)
第七节:倍数与比值;第八节:特殊增长率
【答案汇总】
35现期比重1-5:BBBCA
基期比重1-2:BB
两期比重1-4:CCBB
现期平均数与基期平均数1-4:CDAC
两期平均数1-3:不选不选C
36遇见不一样的自己
Be your better self
37