文档内容
厦门市 2025 届高中毕业班第一次质量检测数学
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题
给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,i(1+i)对应的点位于
A.第一象限B.第二象限C.第三象限D.第四象限
【答案】B
【解析】易知i(1+i)=i−1,所以i(1+i)对应的点为(1,-1),位于第二象限,故选B.
{ | 10 }
2.设集合A= x∈N ∈N ,B={0,1,2,3,4,5},则A∩B=
10−x
A.{0,5}B.{2,5}C.{0,1,5}D.{1,3,5}
【答案】A
【解析】易知集合A={0,5,8,9},所以A∩B={0,5},故选A.
3.已知等轴双曲线C的焦点到其渐近线的距离为1,则C的焦距为
A.√2B.2C.2√2D.4
【答案】C
【解析】设等轴双曲线的焦距为2c,因为焦点到其渐近线的距离为b=1,所以c=√2,
双曲线的焦距为2√2,故选C.
4.已知m,n是两条不同的直线,α,β是两个不同的平面,α∩β=n,则下列说法正确的是
A.若m//α,则m//nB.若m//n,则m//α
C.若m⊥n,则m⊥βD.若m⊥β,则m⊥n
【答案】D
【解析】若m//α,则m,n平行或异面,A选项错误;
若m//n,则m//α或m⊂α,B选项错误;
若m⊥n,则m,β不一定垂直,也可能平行或相交,C选项错误;
若m⊥β,则m⊥n,D选项正确;故选D.
5.已知随机变量X∼N(1,σ2),若P(X≤a)=0.3,且P(a≤X≤a+2)=0.4,则a=1 1
A.-1B.− C.0D.
2 2
【答案】C
【解析】如图所示,P(X≥a+2)=0.3,
所以a+a+2=2×1,
解得a=0,故选C.
π ( π)
6.已知0<α< ,若tan α+ =2(sinα+cosα),则sin2α=
2 4
1 1 3 4
A. B. C. D.
3 2 4 5
【答案】C
( π) 1+tanα sinα+cosα
【解析】tan α+ = = =2(sinα+cosα),因为sinα+cosα≠0,
4 1−tanα cosα−sinα
1 1 3
所以cosα−sinα= ,(cosα−sinα) 2=1−sin2α= ,解得sin2α= ,故选C.
2 4 4
7.过抛物线C:y2=4x的焦点F的直线l交C于A,B两点,交直线x=−1于点P,若⃗PA=⃗AB,
则△OAF与△OBF的面积之比为
1 1 3
A. B. C. D.1
4 2 4
【答案】B
【解析】易知x=−1为C的准线,过A,B分别作x=−1的垂线,垂足分别为M,N,
因为⃗PA=⃗AB,所以2|AM|=|BN|,即2|AF|=|BF|,
1
所以△OAF与△OBF的面积之比为 ,故选B.
2
8.若函数f (x)=ln(eax−6+1)−x的图象关于直线x=3对称,则f (x)的值域为
A.[ln2−3,0)B.[ln2−3,+∞)C.[ln3−2,0)D.[ln3−2,+∞)
【答案】B【解析】f (x)=ln(eax−6+1)−x=ln(e(a−1)x−6+e−x),依题意,f (0)=f (6),
所以ln(e−6+e0)=ln(e6a−6+e−6),所以e−6+e0=e6a−12+e−6,解得a=2,
2
所以f
(x)=ln(ex−6+e−x),因为ex−6+e−x≥2√ex−6×e−x=
,所以f (x)≥2−ln3,
e3
故选B.
二、多项选择题:本题共 3 小题,每小题 6 分,共 18 分.在每小题
给出的四个选项中,有多项符合题目要求.全部选对的得 6 分,部
分选对的得部分分,有选错的得 0 分.
9.已知平面向量a=(2,sinθ),b=(1,cosθ),则
A.a,b不可能垂直
B.a,b不可能共线
C.|a+b|不可能为5
π
D.若θ= ,则a在b方向上的投影向量为2b
2
【答案】ACD
1 3
【解析】a⋅b=2+sinθcosθ≥2− = ,A选项正确;
2 2
若向量a,b共线,则2cosθ−sinθ=0,解得tanθ=2,所以向量a,b可能共线,B选项错误;
a+b=(3,sinθ+cosθ),所以|a+b|=√9+(sinθ+cosθ) 2≤√11<5,C选项正确;
π ab b
若θ= ,则a=(2,1),b=(1,0),所以a在b方向上的投影向量为 ⋅ =2b,D选项正确;
2 |a| |b|
综上所述,应选ACD.
10.药物临床试验是确证新药有效性和安全性必不可少的步骤.在某新药的临床实验
中,志愿者摄入一定量药物后,在较短时间内,血液中药物浓度将达到峰值,当血液中药
物浓度下降至峰值浓度的20%时,需要立刻补充药物.已知某药物的峰值浓度为
120mg/L,为探究某药物在人体中的代谢情况,研究人员统计了血液中药物浓度
y(mg/L)与代谢时间x(ℎ)的相关数据,如下表所示:
x 0 1 2 3 4 5 6 7 8 x´ =4
y 12 110 10 93 82 6 59 47 3 ´y=80
0 3 8 8已知根据表中数据可得到经验回归方程^y=−10.5x+a^,则
A.a^=122B.变量y与x的相关系数r>0
C.当x=5时,残差为-1.5D.代谢约10小时后才需要补充药物
【答案】AC
【解析】因为样本中心点(4,80)在直线y=−10.5x+a^上,所以a^=80+4×10.5=122,A
选项正确;
血液中药物浓度y(mg/L)随代谢时间x(ℎ)的增大而减小,所以变量y与x的相关系数
r>0,B选项错误;
当x=5时,^y=−10.5×5+122=69.5,残差为68−69.5=−1.5,C选项正确;
令−10.5×x+122=120×0.2,解得x≈9.33,D选项错误;综上所述,应选AC.
11.已知定义在(0,+∞)上的函数f (x)满足f (x+1)=2f (x)+[x],其中[x]表示不超过x的最
大整数,如[1.9]=1,[3]=3.当00,|φ|<π)的图象经过 , , ,− 两点,若
3 2 3 2
(2π 4π)
f (x)在区间 , 上单调递减,则ω=_____;φ=_____.
3 3
1 π
【答案】 ; (第一空3分,第二空2分)
2 2
{
sin(ωπ+φ)=0
【解析】依题意,f (π)=0,所以 ( 2π ) 1,
sin ω +φ =
3 2
{ ωπ+φ=(2k+1)π
即 2π π,
ω +φ=(2k+1)π−
3 6
1 π π 1 π
解得ω= ,所以 +φ=(2k+1)π,因为|φ|<π,所以|φ|= ,应填 , ;
2 2 2 2 2
14.从集合U={1,2,3,4}的所有非空子集中任选两个,则选中的两个子集的交集为空
集的概率为_____.
5
【答案】
21
【解析】设A⊆U,B⊆U,且A∩B=⌀,
易知集合U的非空子集个数为24−1=15,任取两个集合A,B共有C2 =105种选法.
15
(方法一)①若card(A∪B)=2,则共有C2=6种选法.;
4
②若card(A∪B)=3,从4个元素里选3个,再分成两组(不平均),有C3C1=12种选法;
4 3
C2
③若card(A∪B)=4,4个元素平均分为两组共有 4=3种;不平均分组共有C1=3种,
A2 3
2
小计共有7种选法;6+12+7 5
所以选中的两个子集的交集为空集的概率为P= = .
105 21
(方法二)①当card(A)=1时,4个元素里任选一个放入集合A中,集合B共有23−1=7种
情况,故有C1×7=28种情况;
4
②当card(A)=2时,4个元素里任选两个放入集合A中,集合B共有22−1=3种情况,
故有C2×3=18种情况;
4
③当card(A)=3时,4个元素里任选三个放入集合A中,集合B共有21−1=1种情况,
1
故有C3×1=4种情况;总共有 (28+18+4)=25种情况,
4 2
25 5
所以选中的两个子集的交集为空集的概率为P= = .
105 21
(方法三)对于集合U中的任意元素x均有x∈A,且x∉B;x∈B,且x∉A;x∉(A∪B)
1
这三种选法,再减去集合A,B其中一个为空集的情况,故共有 (34−24−24+1)=25种,
2
25 5 5
所以选中的两个子集的交集为空集的概率为P= = .应填 ;
105 21 21
四、解答题:本题共 5 小题,共 77 分.解答应写出文字说明、证
明过程或演算步骤.
15.(13分)在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC=(√2b−c)cosA.
(1)求A;
3√10
(2)设D为边AB的中点,若c=2,且sin∠CDB= ,求a.
10
π √34 √10
【答案】(1) ;(2) 或 .
4 4 2
【解析】(1)方法1:由正弦定理可得sin AcosC−√2sinB⋅cosA+sinC⋅cosA=02分
即sin(A+C)−2sinB⋅cosA=0,即sinB−√2sinB⋅cosA=0..3分
√2
因为B∈(0,π),可得sinB≠0,所以cosA= ,4分
2
π
因为A∈(0,π),所以A= .·5分
4
评分细则:方法1:分两个过程(3分+2分)
过程1:边化角:利用两角和的正弦公式及sinB=sin(A+C)化解(3分).
√2 π
过程2:求值:求出cosA= (1分),求出A= (1分)
2 4
a2+b2−c2 b2+c2−a2
方法2:由余弦定理可得,cosC= ,cosA= ,·1分
2ab 2bc
a2+b2−c2 b2+c2−a2
所以a =(√2b−c) ,整理得,b2+c2−a2=√2bc,.3分
2ab 2bc
b2+c2−a2 √2
所以cosA= = ,·4分
bc 2
π
因为02=|C C |,所以圆心M的轨迹为椭圆,.3分易知椭圆C的长轴长为
1 2 1 2
x2 y2
2a=4,焦距为2c=2,所以a=2,c=1,所以b2=a2−c2=3,·5分所以C的方程为 + =1.6
4 3
分设圆M半径表达|MC |,|MC |(2分)由椭圆定义证明M轨迹为椭圆(1分)计算出
1 2
a,b,c,(2分)有计算错误酌情给分写出C的方程(1分).(2)方法一:设P(x ,y ),Q(x ,y )
1 1 2 2
,由⃗OP⋅⃗OQ=0可知,x x + y y =0,当直线PQ的斜率不存在时,设直线PQ:x=t,则
1 2 1 2
{
x=t,
3t2
(
3t2
)
P(t,y),Q(t,−y),由 x2 y2 可得,y2=3− ,所以x x + y y =t2− 3− =0,解
+ =1 4 1 2 1 2 4
4 3
12 π 48 12π
得t2= ,此时,圆E的面积为 × = .-8分当直线PQ的斜率存在时,设直线
7 4 7 7
{y=kx+m,
PQ:y=kx+m,由 x2 y2 可得,(3+4k2)x2+8kmx+4m2−12=0,所以
+ =1
4 3
−8km 4m2−12
x +x = ,x x = ,10分所以
1 2 3+4k2 1 2 3+4k2
4m2−12 −8km −12k2+7m2−12
x x + y y =x x +(kx +m)(kx +m)=(k2+1)x x +km(x +x )+m2=(k2+1) +km +m2= =0
1 2 1 2 1 2 1 2 1 2 1 2 3+4k2 3+4k2 3+4k2
,所以−12k2+7m2−12=0,即7m2=12+12k2,12分代入
Δ=64k2m2−4(3+4k2)(4m2−12)=16(12k2+9−3m2)>0,所以
√16(12k2+9−3m2) √48 √16k2+9 √48√ k2 √48
|PQ|=√1+k2|x −x |=√1+k2 = √1+k2 = 1+ ≥ ,
1 2 3+4k2 7 3+4k2 7 (3+4k2) 2 7
√48 π 48 12π
.14分当且仅当k2=0时,|PQ|取得最小值 ,所以圆E面积的最小值为 × =
7 4 7 7
.·15分考虑直线PQ的斜率不存在的情况,并计算圆E的面积(2分)联立直线PQ与椭
圆,设点写
出韦达关系(2分)由OP,OQ垂直关系,得到k,m的关系式(2分)写出|PQ|的表达式
(1分),求出最小值(1分),结论(1分)
方法二:因为以PQ为直径的圆E经过坐标原点O,所以OP⊥OQ,.7分①当直线OP,OQ中有一条斜率不存在时,则另一条斜率为0,
√7 7π
易知|PQ| 2=a2+b2=7,所以圆E的半径为 ,所以圆E的面积为 .·8分
2 4
②若直线OP,OQ的斜率均存在,
1
设直线OP:y=kx,直线OQ:y=− x,P(x ,y ),Q(x ,y ),
k 1 1 2 2
{x2 y2
+ =1, 12
所以由 4 3 可得x ❑ 2= ,
1 4k2+3
y=kx
12k2
同理可得x ❑ 2= ,10分
2 4+3k2
所以|PQ| 2=|OP| 2+|OQ| 2=(1+k2)x ❑ 2+ ( 1+ 1 ) x ❑ 2 ,
1 k2 2
12(1+k2) ( 1 ) 12k2 7k2
= + 1+ =7− ,·12分
4k2+3 k2 4+3k2 (4k2+3)(4+3k2)
7 7 48
|PQ| 2=7− ≥7− =
所以 12k2+ 12 +25 2 √ 12k2× 12 +25 7 ,·14分
k2 k2
48
当且仅当k2=1时,|PQ| 2取得最小值 ,
7
π 48 12π
所以此时,圆E面积的最小值为 × = ,
4 7 7
7π 12π 12π
因为 > ,所以圆E面积的最小值为 .·15分
4 7 7
考虑直线OP或者OQ斜率不存在的情况,并计算圆E的面积(2分)
若计算错误,写出了OP与OQ的垂直关系,给1分.
联立直线OP与椭圆,得到x ❑ 2,x ❑ 2与k的关系(2分)
1 2
写出|PQ|的表达式(2分),求出最小值(2分),结论(1分)
方法三:设P(2cosα,√3sinα),Q(2cosβ,√3sinβ),·7分
因为OP⊥OQ,所以⃗OP⋅⃗OQ=4cosαcosβ+3sinαsinβ=0,-8分
所以|PQ| 2=(2cosα−2cosβ) 2+(√3sinα−√3sinβ) 2=6+cos2α+cos2β−(8cosαcosβ+6sinαsinβ)=6+cos2α+cos2β,10分
因为4cosαcosβ=−3sinαsinβ,所以
16cos2αcos2β=9sin2αsin2β=9(1−cos2α)(1−cos2β),
整理得,7cos2αcos2β=9[1−(cos2α+cos2β)],·11分
(cos2α+cos2β) 2
由基本不等式,得cos2αcos2β≤ ,
4
7(cos2α+cos2β) 2
所以9[1−(cos2α+cos2β)]≤ ,13分
4
7t2 6
设t=cos2α+cos2β>0,则9(1−t)≤ ,即(7t−6)(t+6)≥0,解得t≥ ,·14分
4 7
48
所以|PQ|
2=6+cos2α+cos2β=6+t≥
,
7
π 48 12π
所以圆E面积的最小值为 × = .·15分
4 7 7
由参数方程分别写出P,Q的坐标(1分)
由OP与OQ的垂直关系,得到两参数关系(1分)
写出|PQ|的表达式(2分),求出最小值(4分)计算过程酌情给分,结论(1分)
方法4:设|OP|=m,P(mcosα,msinα),
( ( π) ( π))
因为OP⊥OQ,所以可设|OQ|=n,且Q ncos α+ ,msin α+ ,·8分
2 2
m2cos2α m2sin2α
因为点P(mcosα,msinα)在C上,所以 + =1,
4 3
1 cos2α sin2α
所以 = + ,
m2 4 3
n2cos2( α+ π) n2sin2( α+ π) 1 sin2α cos2α
同理可得, 2 2 ,所以 = + ,10分
+ =1 n2 4 3
4 3
1 1 cos2α sin2α sin2α cos2α 7
所以 + = + + + = ,12分
m2 n2 4 3 4 3 12
所以|PQ| 2=|OP| 2+|OQ| 2=m2+n2= 12 (m2+n2) ( 1 + 1 )
7 m2 n212( n2 m2 ) 12( √ n2 m2) 48
= 2+ + ≥ 2+2 × = ,·14分
7 m2 n2 7 m2 n2 7
π 3π 5π 7π
当且仅当m=n,α= ,或α= ,α= ,α= 时等号成立,
4 4 4 4
π 48 12π
所以圆E面积的最小值为 × = ..15分
4 7 7
写出P,Q的坐标(2分)
1 1 7
分别写出m2与n2的表达式(2分),得到 + = (2分)
m2 n2 12
求出|PQ|的最值(2分),结论(1分).
18.(17分)设函数f (x)=x(ex−a) 2 .
(1)当a=0时,求f (x)的单调区间;
(2)若f (x)单调递增,求a的取值范围;
1
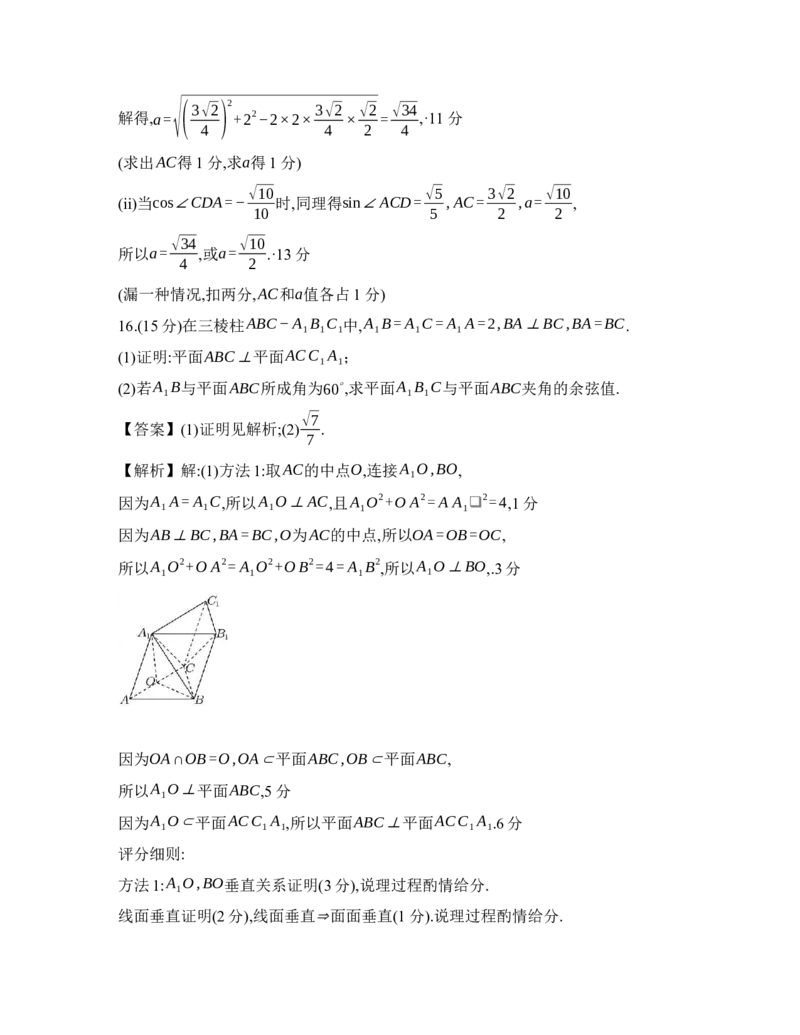
(3)当00,f (x)单调递增,-3分
2
( 1 ) ( 1)
所以f (x)的单调递增区间为 − ,+∞ ,单调递减区间为 −∞,− .4分
2 2
求导正确(1分),f (x)单调性(2分),可根据具体书写形式酌情给分,结论(1分).
(2)f'(x)=(ex−a)(2xex+ex−a),
设g(x)=2xex+ex−a,g'(x)=2xex+ex=(2x+3)ex,·5分( 3) ( 3 )
当x∈ −∞,− 时,g'(x)<0,g(x)单调递减,当x∈ − ,+∞ 时,g'(x)>0,g(x)单调递
2 2
增,当x=− 3
2
时,g(x)取得极小值g ( − 3
2
) =−2e − 3 2−a,(i)所以当
a≤−2e
− 3
2
时,
3
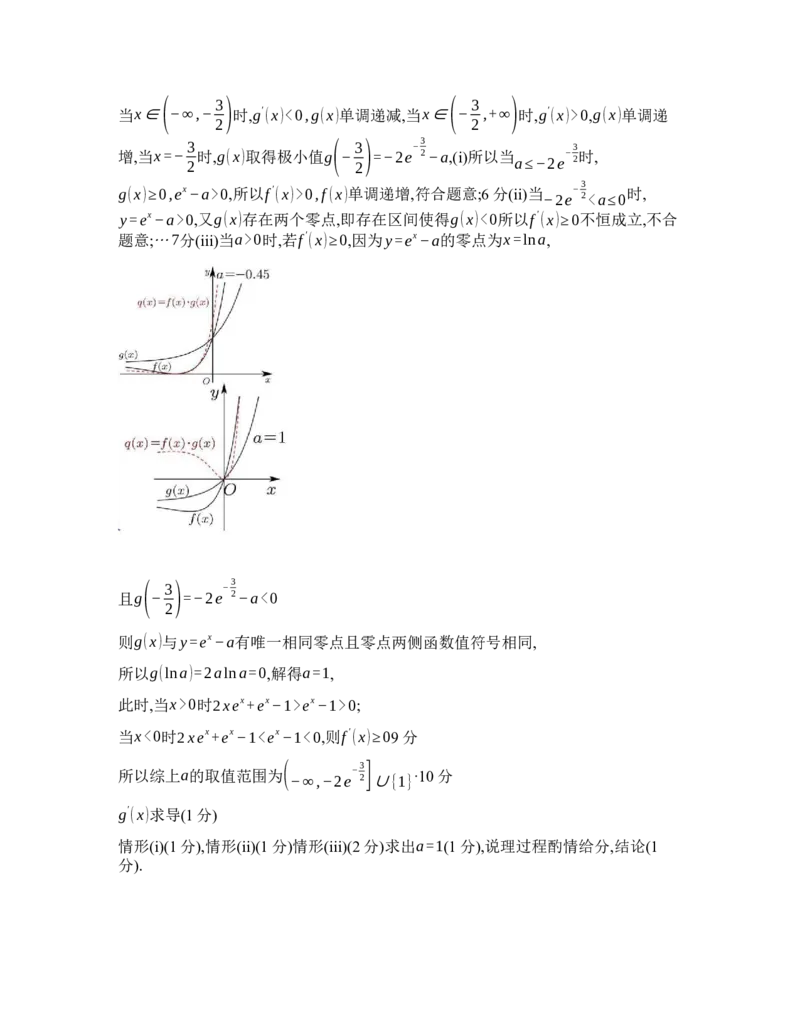
g(x)≥0,ex−a>0,所以f'(x)>0,f (x)单调递增,符合题意;6分(ii)当
−2e
−
20,又g(x)存在两个零点,即存在区间使得g(x)<0所以f'(x)≥0不恒成立,不合
题意;⋯7分(iii)当a>0时,若f'(x)≥0,因为y=ex−a的零点为x=lna,
3
且g ( − 3) =−2e − 2−a<0
2
则g(x)与y=ex−a有唯一相同零点且零点两侧函数值符号相同,
所以g(lna)=2alna=0,解得a=1,
此时,当x>0时2xex+ex−1>ex−1>0;
当x<0时2xex+ex−10,设x 为g(x)的零点,则− lna,·11分
1
所以当x∈(−∞,lna)时,y=ex−a<0,g(x)<0,所以f'(x)>0,f (x)单调递增,
当x∈(lna,x )时,y=ex−a>0,g(x)<0,所以f'(x)<0,f (x)单调递减,
1
当x∈(x ,+∞)时,y=ex−a>0,g(x)>0,所以f'(x)>0,f (x)单调递增,13分
1
所以x =x ,且2x ex 0+ex 0−a=0,即ex 0−a=−2x ex 0,·14分
1 0 0 0
所以f (x )=(ex 0−a) 2 x =(−2x ex 0) 2 x =4x ❑ 3e2x 0,
0 0 0 0 0
设ℎ(x)=4x3e2x(
−
1
0,ℎ(x)单调递增,
2
( 1) 1 1
所以ℎ(x)< ℎ(0)=0,ℎ(x)> ℎ − =− ,16分所以− lna(1分),讨论f (x)单调性(2分),说理过程酌情给分;
1
判断x =x (1分),写出f (x )的表达式(1分),求导判断单调性(1分),结论(1分).
1 0 0
19.(17分)若数列{a }满足数列{|a −a |}是等差数列,则称{a }为“绝对等差数列”,
n n+1 n n
{|a −a |}的公差称为{a }的“绝对公差”.
n+1 n n
(1)若“绝对等差数列”{a }的“绝对公差”为2,且a −a =4,求a −a 的值;
n 3 1 2 1
(2)已知“绝对等差数列”{d }满足d =0,|d −d |=1,且{d }的“绝对公差”为1,记S
n 1 2 1 n n
为{d }的前n项和,
n
(i)若d −d =(−1) n−1n,求S ;
n+1 n 2n
(ii)证明:对任意给定的正整数m,总存在d ,d ,⋯,d 满足|S |≤4.
1 2 m m
(2)(i)S =n;(2)见解析.
2n
【解析】(1)设|a −a|=x≥0,则|a −a |=x+2,
2 1 3 2
因为a −a =(a −a )+(a −a )=4,2分
3 1 3 2 2 1
若a −a 与a −a 均为负数,则−x−x−2=4,解得x=−3,不合题意;
2 1 3 2
若a −a 与a −a 一正一负,则a −a =2或-2,不合题意;
2 1 3 2 3 1
所以a −a =x,a −a =x+2,-4分
2 1 3 2所以2x+2=4,解得x=1,故a −a =1.·5分
2 1
a −a 拆解成a −a +a −a (2分),有设参过程正确理解题意给1分,
3 1 3 2 2 1
a −a 与a −a 正负讨论(2分),直接判断为正可扣1分,结论(1分).
2 1 3 2
(2)(i)d =d +(d −d )+⋯+(d −d )=1−2+3−4+⋯+(2n−1)=n,·6分
2n 1 2 1 2n 2n−1
因为d =d −(2n−1)=1−n.7分
2n−1 2n
所以S =(d +d )+(d +d )+⋯+(d +d )=n.-8分
2n 1 2 3 4 2n−1 2n
求得d =n(1分),d =1−n(1分),结论(1分)
2n 2n−1
若有其他求解方法,酌情给分.
(ii)依题意,|d −d |=n,记d −d =nb ,其中b ∈{−1,1},
n+1 n n+1 n n n
m−1
①若m为奇数,令b =(−1) n−1 ,由(i)可知,S = ,9分
n m−1 2
m−1
因为d =d +(d −d )+⋯+(d −d )=0+1−2+3−4+⋯+m−2−(m−1)=− ,
m 1 2 1 m m−1 2
m−1 m−1
所以S =S +d = − =0≤4,符合题意;
m m−1 m 2 2
所以对任意给定的奇数m,存在满足a −a =(−1) n−1n的{a }使得|S |≤4.10分
n+1 n n m
m−1
m为奇数情形(2分),其中S = (1分),S =0(1分)
m−1 2 m
②若m为偶数,因为d =d +(d −d )+⋯+(d −d )=b +2b +⋯+(m−1)b ,
m 1 2 1 m m−1 1 2 m−1
d =d +(d −d )+⋯+(d −d )=b +2b +⋯+(m−2)b ,
m−1 1 2 1 m−1 m−2 1 2 m−2
.......
d =d +(d −d )=b ,
2 1 2 1 1
d =0,
1
m−1
累加得S =(m−1)b +2(m−2)b +⋯+k(m−k)b +⋯+(m−1)b =∑ k(m−k)b ⋅11
m 1 2 k m−1 k
k=1
分
m
由(i)知,令b =(−1) n−1可得,S = .
n m 2
m
若m≤8,则|S |= ≤4,符合题意,故下面只讨论m≥10的情况.·12分
m 2m−1
写出S =∑ k(m−k)b (1分),讨论m≤8的情况满足题意(1分)
m k
k=1
m−1 m2m−1 m−1 (m ) 2
易知S =∑ k(m−k)b = ∑ b −∑ −k b ,·13分
m k 4 k 2 k
k=1 k=1 k=1
m
当k为大于1的奇数时,b =−1,b =1,设此时的k= j= −i,即b =−1,b =1,
k−1 k 2 j−1 j
构造新数列{c },其中c =−b =1,c =−b =−1,
n j−1 j−1 j j
m−1 m−1
其余各项均不变即c =b (k≠ j−1, j),所以∑ c =∑ b ,
k k k k
k=1 k=1
记{b }调整为{c }后该数列的前m项和为S ❑ ' ,
n n m
m−1 (m ) 2 m−1 (m ) 2 (m ) 2 (m ) 2 m−1 (m ) 2
∑ −k c =∑ −k b −2 − j+1 b −2 −k b =∑ −k b +
2 k 2 k 2 j−1 2 j 2 k
k=1 k=1 k=1
2(i+1) 2−2(i) 2则
S ❑ '= m2m ∑ −1 c − m ∑ −1 (m −k ) 2 c = [m2m ∑ −1 b − m ∑ −1 (m −k ) 2 b ] −4i−2= m −4i−2·15
m 4 k 2 k 4 k 2 k 2
k=1 k=1 k=1 k=1
分
写出S = m2m ∑ −1 b − m ∑ −1 (m −k ) 2 b (1分),构造新数列{c },得到S ❑ '的表达式(2分)有
m 4 k 2 k n m
k=1 k=1
调整相邻两项的思路给1分,其他表达书写过程酌情给分.
m m−12 m+4
令−4≤ −4i−2≤4,解得 ≤i≤ ,·16分
2 8 8
m [m−12] m [m+4]
则对任意给定的偶数m,当j= − −1,或j= − 时,其中[x]为不超过x
2 8 2 8
的最大整数,即存在{c }满足|S |≤4,所以综上所述,对任意给定的正整数m,总存在一
n m
个{a }满足|S |≤4·17分
n m
依题意,解得i的范围(1分),说明存在满足题意的j和结论(1分)
(3)参数方法二:依题意|d −d |=n,设d −d =nb ,其中b ∈{−1,1}.因为
n+1 n n+1 n n n
d =d +(d −d )+⋯+(d −d ),所以
n 1 2 1 n n−1
m−1
S =(d −d )+2(d −d )+⋯+(m−1)(d −d )=∑ i(m−i)b .10分
m m m−1 m−1 m−2 2 1 i
i=1
m−1
写出|d −d |=n(1分),写出S =∑ i(m−i)b的表达式(1分)
n+1 n m i
i=1(i)若m=2k+1为奇数.因为i(m−i)=(m−i)[m−(m−i)],所以当b =(−1) n−1时,|S |=0≤4,
n m
符合题意;·12分
m为奇数情形(2分)
(ii)若m=2k为偶数.由(2)知,当b =(−1) n−1时,S =k.若k≤4,当b =(−1) n−1时,|S |=k≤4,
n m n m
符合题意,故下面只讨论k>4的情况.·13分
讨论m≤8的情况满足题意(1分)
设正整数j满足2 j+1≤k.若将b =−1和b =1的值对调,S 的改变量
2j 2j+1 m
ΔS =2[2 j(m−2 j)−(2 j+1)(m−2 j−1)]=8 j−2m+2,
m
所以此时的前m项和为S' =S +ΔS =8 j+2−3k.15分
m m m
调整相邻两项系数为相反数,求得S' (2分)
m
有调整相邻两项的思路给1分,其他表达书写过程酌情给分
记[x]为不超过x的最大整数.
[k−1] [k−1]
当j取遍1,2,⋯, 时,S' 取遍10−3k,18−3k,⋯⋯,8 +2−3k.
2 m 2
[k−1]
因为10−3k≤−5,8 +2−3k≥k−2≥3,且上述序列中相邻两数之差为8,
2
{ [k−1]}
所以存在j∈ 1,2,⋯, ,使得S' ∈{−4,−3,−2,−1,0,1,2,3,4},符合题
2 m
意..17分
证明存在满足题意的调整方案(1分),结论(1分).