补习数学答案（理科）(1)_2023年10月_0210月合集_2024届四川省射洪中学高三上学期10月月考试题（补习班）_四川省射洪中学2024届高三上学期10月月考试题（补习班）理科数学

射洪中学高2021级补习班高三10月月考 数学(理)试题答案 1.B【详解】由A=x∈Z-1≤x≤3  ，可得A=-1,0,1,2,3  ， 由B=xx2≤2  ，可得B=x- 2≤x≤ 2  ，所以A∩B=-1,0,1  .故选：B 2.D【详解】对于A，∵y=cosx在π,2π  上单调递增，∴当2π>a>b>π时，cosa>cosb，A错误； 对于B，∵y=2x在0,+∞  上单调递增，∴2a>2b，即2a-2b>0，B错误； 1 对于C，∵y= 在0,+∞ x  1 1 上单调递减，∴ < ，C错误； a b 对于D，∵y=x3在0,+∞  上单调递增，∴a3>b3，D正确.故选：D. 3.D【详解】由题意得¬p是真命题，即∀x∈R，3ax2+2ax+1>0， 当a=0时，1>0符合题意； 当a≠0时，有a>0，且Δ=(2a)2-4⋅3a<0，解得00,ex>e0=1，故ex+1>0,ex-1>0， ∴f(x)>0；综上所述：A正确，B、C、D错误.故选：A. 6.C T 7π π π 7.A【详解】依题意，A= 2， = - = ，故T=π， 4 12 3 4 2π 7π 故ω= =2，故f(x)= 2sin(2x+φ)，将 ,- 2 π 12  7π 3π 代入可知，2× +φ= +2kπ(k∈Z)， 12 2 π π 解得φ= +2kπ(k∈Z)，故f(x)= 2sin2x+ 3 3  π ，故g(x)=fx- 2  2π = 2sin2x- 3  ， 5π 则g 12  π 2 = 2sin = 故选：A. 6 2 补习班 理科答案 第1页 共7页8.B【详解】∀x∈R， 9x2+1>3x  ≥3x，则 9x2+1-3x>0恒成立， 又因为fx  +f-x  =ln 9x2+1-3x  +ln 9x2+1+3x  +x-x+2 =ln9x2+1-9x2  +2=2， 因为a+b=2023，则b-2025  +a+2  =0， 因此，fb-2025  +fa+2  =2.故选：B 9.A【详解】因为tan2α-tanα  ⋅cos2α=2， sin2α 所以 -tanα cos2α  sinα ⋅cos2α=2，所以sin2α- ⋅cos2α=2， cosα sinα 即2sinαcosα- ⋅2cos2α-1 cosα  =2， sinα sinα 即2sinαcosα-2sinαcosα+ =2，即 =tanα=2.故选：A cosα cosα 10.D【详解】因为fx+6  =-fx+3  =fx  ，所以fx  是以6为周期的函数， 所以f2023  =f337×6+1  =f1  =f-2+3  =-f-2  2π =- 2-2+sin- 3      1 3 =- + . 4 2 1 11.B【详解】由 x ． 729 1 又因为0xex， 设fx  =2ax-a,gx  =xex，则直线fx  1 =2ax-a过定点 ,0 2  ， 由题意得函数gx  =xex的图象在直线fx  =2ax-a的下方． ∵gx  =xex，∴gx  =x+1  ex． 设直线fx  =2ax-a与曲线gx  =xex相切于点m,n  2a=m+1 ，则有{  em ， mem=2am-a 1 消去a整理得2m2-m-1=0，解得m=- 或m=1(舍去)， 2 1 故切线的斜率为2a=- +1 2  -1 1 -1 e e e 2= e 2= ，解得a= ． 2 2e 4e 又由题意知原不等式无整数解，结合图象可得当x=-1时，f-1  =-3a,g-1  =-e-1， 由f-1  =g-1  1 解得a= ， 3e 当直线fx  1 =2ax-a绕着点 ,0 2  1 e 旋转时可得 ≤a< ， 3e 4e 故实数a的取值范围是  1 , e 3e 4e  ．选B． 补习班 理科答案 第2页 共7页1 1 13.- 或 【详解】根据题意可设fx 2 2  =xm,m∈R  ，由题可知2m=4，解得m=2，则fx  =x2， 又fa  1 1 1 1 1 1 = ，即a2= ，解得a=- 或 .故答案为：- 或 . 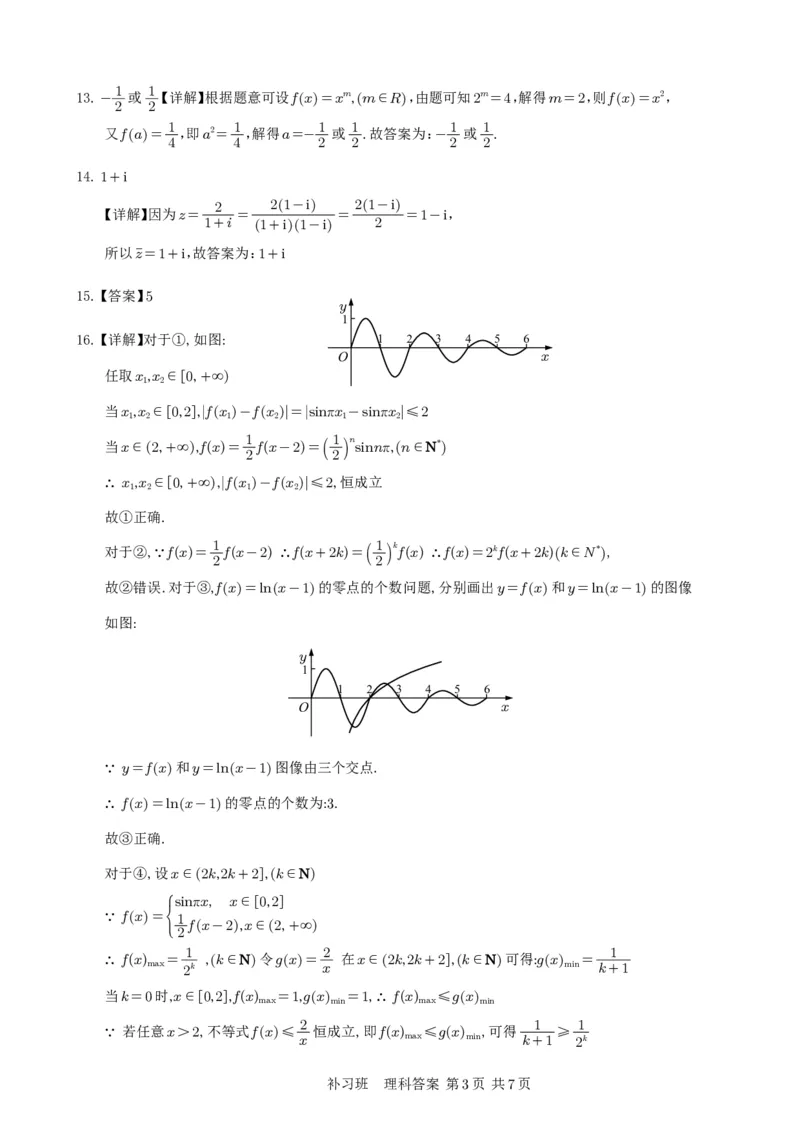4 4 2 2 2 2 14.1+i 2 21-i 【详解】因为z= = 1+i  1+i  1-i  21-i =  =1-i， 2  所以z=1+i，故答案为：1+i 15.【答案】5 16.【详解】对于①,如图: 任取x 1 ,x 2 ∈0,+∞  当x 1 ,x 2 ∈0,2  , fx 1  -fx 2    =sinπx 1 -sinπx 2  ≤2 当x∈2,+∞  1 1 ,f(x)= f(x-2)= 2 2  n sinnπ,n∈N*  ∴ x 1 ,x 2 ∈0,+∞  , fx 1  -fx 2    ≤2,恒成立 故①正确. 1 1 对于②,∵f(x)= f(x-2) ∴f(x+2k)= 2 2  k f(x) ∴f(x)=2kf(x+2k)k∈N*  , 故②错误.对于③,fx  =lnx-1  的零点的个数问题,分别画出y=fx  和y=lnx-1  的图像 如图: y 1 1 2 3 4 5 6 O x ∵ y=fx  和y=lnx-1  图像由三个交点. ∴ fx  =lnx-1  的零点的个数为:3. 故③正确. 对于④,设x∈2k,2k+2  ,k∈N  ∵ fx  sinπx, x∈0,2 =  1 fx-2 2  ,x∈2,+∞    1 ∴ f(x) max = 2k ,k∈N  令gx  2 = 在x∈2k,2k+2 x  ,k∈N  可得:gx  1 = min k+1 当k=0时,x∈0,2  ,f(x) max =1,gx  min =1,∴ f(x) max ≤gx  min ∵ 若任意x>2,不等式fx  2 ≤ x 恒成立,即f(x) max ≤gx  y 1 1 2 3 4 5 6 O x 1 1 ,可得 ≥ min k+1 2k 补习班 理科答案 第3页 共7页1 1 求证:当k≥1, ≥ ,化简可得:2k≥k+1， k+1 2k 设函数T(k)=2k-k-1,则T(k)=2kln2-1≥0 ∴当k≥1时,T(k)单调递增,可得T(k)≥T(1)=0， 1 1 ∴ T(k)=2k-k-1≥0∴2k≥k+1 即: ≥ ， k+1 2k 综上所述,对任意x>0,不等式fx  2 ≤ 恒成立.故④正确.故答案为:①③④. x 17.解：1  ∵ A={x|x-5<2x-5 ， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分 m+1<-2 m≤-2  解得：m>-4， m<-3 ∴m的取值范围是{m|-40，fx  单调递增； 又f-1  =11,f2  =-16,f3  =-9， 故fx  在-1,3  上的值域为-16,11  ； ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分 g(x)=mx+5(m>0)，当x∈-1，3  ，gx  单调递增， 故gx  值域为-m+5,3m+5  ； ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分 根据题意-m+5，3m+5  是-16，11  的子集， 故-m+5≥-16,3m+5≤11，m>0，解得m∈0，2  ， 故实数m的取值范围为0，2  ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12分 π 20.【详解】(1)因为f(x)= 3sin(π+x)sinx- 2  π +cos2 +x 2  1 - ， 2 所以f(x)= 3-sinx  -cosx  1 +sin2x- ， 2 3 1-cos2x 1 = sin2x+ - ， 2 2 2 3 1 π = sin2x- cos2x=sin2x- 2 2 6  ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分 π π π π π 令- +2kπ≤2x- ≤ +2kπ，解得- +kπ≤x≤ +kπ， 2 6 2 6 3 所以fx  π π 的单调递增区间： kπ- ,kπ+  6 3  ，(k∈Z)；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分 (2)因为f(A)=1，所以fA  π =sin2A- 6  =1， π 又因为A∈(0，π)，所以A= ， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分 3 b2+c2-4 1 在三角形ABC中，利用余弦定理得cosA= = ， 2bc 2 整理得：b2+c2-4=bc， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分 又因为b2+c2≥2bc，所以b2+c2-4≥2bc-4，即bc≥2bc-4，⋯⋯⋯⋯⋯⋯⋯⋯10分 1 3 所以bc≤4，当且仅当b=c时等号成立，S = bcsinA= bc △ABC 2 4 所以S ≤ 3，当且仅当a=b=c=2时，S 取得最大值 3.⋯⋯⋯⋯⋯⋯⋯12分 △ABC △ABC 补习班 理科答案 第5页 共7页21.解：(1) 当t=0时，f(x)=x-ex+1，f(x)=1-ex，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分 当x<0，f(x)>0，f(x)在(-∞,0)内单增； 当x>0，f(x)<0，f(x)在(0,+∞)内单减， f(x) =f(0)=0. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2分 max (2)由f(x)=1，得xetx=ex，即x=ex(1-t)>0，原方程无负实根， lnx 故有 =1-t，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分 x lnx 1-lnx 令g(x)= ，g(x)= ， x x2 当00，f(x)在(0,e)内单增； 当x>0，f(x)<0，f(x)在(e,+∞)内单增， 1 则g(x) =g(e)= ，而当x→0时，g(x)→-∞， max e 1 故g(x)值域为-∞, e  . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 1 方程f(x)=1无正实根等价于当1-t∉-∞, e  1 1 ，即1-t> ，也即t<1- ， e e 1 综上，当t<1- 时，方程f(x)=1无实根. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分 e (2)f(x)=etx+txetx-ex=etx[1+tx-e(1-t)x]， 由题设知∀x>0，f(x)≤0，无妨取x=1，有f(1)=et(1+t-e1-t)≤0， 即e1-t≥1+t>1=e0，也即t<1.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分 1 x x x 1°当t≤ 时，且x>0，有f(x)=etx[1+tx-e(1-t)x]≤e21+ -e2 2 2  ， x x 由(Ⅰ)知1+x-ex<0，也有1+ -e2<0， 2 故f(x)<0，函数f(x)在(0,+∞)内单减. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分 1 1 t 1 t 2°当 1，即 ln >0， 2 2 1-t 1-t 1-t 令h(x)=1+tx-e(1-t)x，h(0)=0， t h(x)=t-(1-t)e(1-t)x=(1-t)  -e(1-t)x 1-t  ， 1 t 1 t 当00，h(x)在0, ln 1-t 1-t 1-t 1-t  内单增， 1 t h(x)>h(0)=0，此时f(x)>0，f(x)在0, ln 1-t 1-t  内单增， f(x)>f(0)=0，与题设矛盾. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11分 1 综上，当且仅当t≤ 时，函数f(x)是(0,+∞)内的减函数.⋯⋯⋯⋯⋯⋯⋯⋯12分 2 1 (注：不能说明当t> 时命题不成立，最多得9分) 2 补习班 理科答案 第6页 共7页22.(1)由于  x=2- 3t ，消t得2- 3y=x， y=t 即x+ 3y-2=0， ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分 由ρ⋅sin2θ=6cosθ得ρ2⋅sin2θ=6ρcosθ， ∴曲线C的直角坐标方程是：y2=6x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分 3 (2)将直线l:   x=2- 3t 化为标准形式   x=2- 2 t (t为参数)， ⋯⋯⋯⋯⋯⋯⋯⋯6分 y=t 1 y= t 2 1 代入y2=6x， t 2  2 3 =62- t 2  并化简得t2+12 3t-48=0， ⋯⋯⋯⋯⋯⋯⋯7分 Δ=624>0，设A，B对应参数为t，t，tt=-48<0，t+t=-12 3,⋯⋯⋯⋯⋯⋯⋯⋯8分 1 2 1 2 1 2 所以AM  +BM  =t 1  +t 2  =t 1 -t 2  = (t+t)2-4tt =4 39 ⋯⋯⋯⋯⋯⋯⋯⋯10分 1 2 1 2 补习班 理科答案 第7页 共7页