文档内容
五年(2019-2023)年高考真题分项汇编
专题 05 立体几何(选填题)
立体几何在文科数高考中属于重点知识点,难度中等。包含题型主要是
1 空间几何体基本性质及表面积体积
2 空间几何题三视图
3 空间几何体内切球外接球的应用
4 空间几何体性质综合应用
考点 01 空间几何体基本性质及表面积体积
1.(2023·年全国甲卷)在三棱锥 中, 是边长为2的等边三角形, ,
则该棱锥的体积为( )
A.1 B. C.2 D.3
2.(2023·北京·统考高考真题)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以
勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两
个面是全等的等腰三角形.若 ,且等腰梯形所在的平面、等腰三角形所在的平面
与平面 的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
A. B.
C. D.
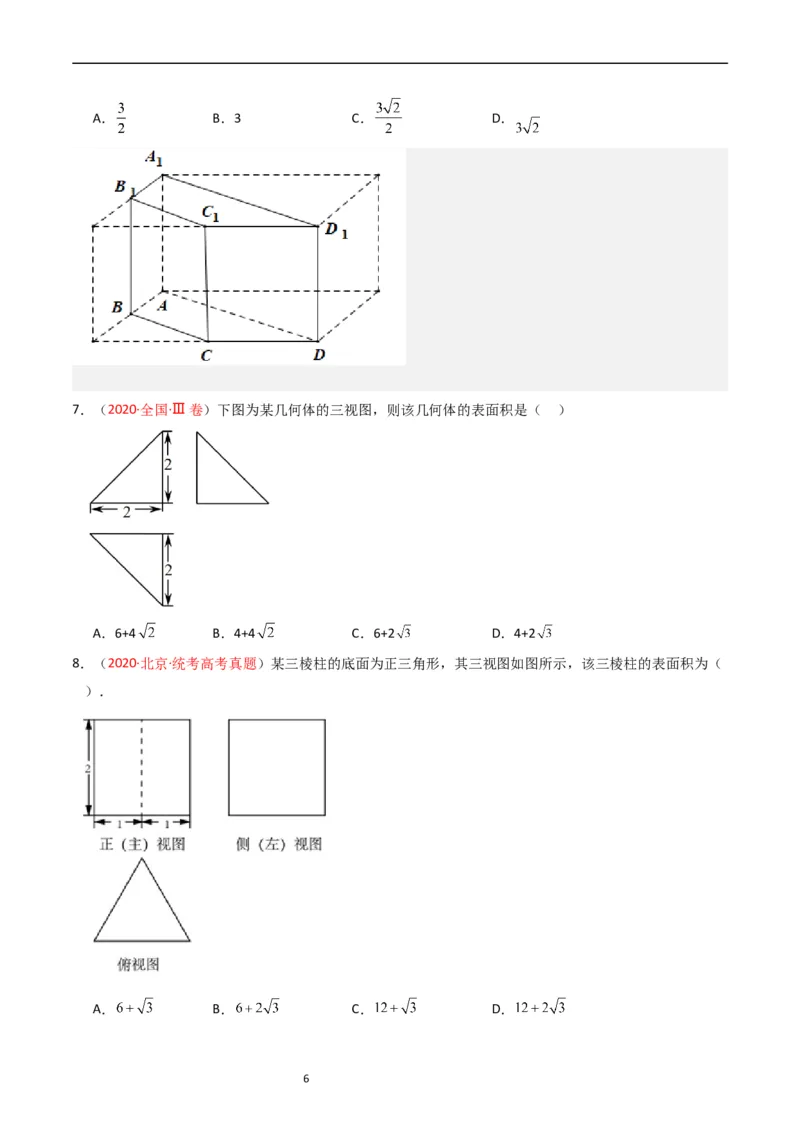
3.(2022·全国乙卷)在正方体 中,E,F分别为 的中点,则( )
A.平面 平面 B.平面 平面
C.平面 平面 D.平面 平面
4.(2022·全国甲卷)在长方体 中,已知 与平面 和平面 所成的角均为
,则( )
1A. B.AB与平面 所成的角为
C. D. 与平面 所成的角为
5.(2021·全国乙卷)在正方体 中,P为 的中点,则直线 与 所成的角为( )
A. B. C. D.
6.(2021·年全国新高考Ⅰ卷)已知圆锥的底面半径为 ,其侧面展开图为一个半圆,则该圆锥的母线长
为( )
A. B. C. D.
7.(2021年全国高考Ⅱ卷)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
8.(2021·年全国高考Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,
以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与
底面正方形的边长的比值为( )
A. B. C. D.
9.(2019·年全国高考Ⅰ卷)设 , 为两个平面,则 的充要条件是
A. 内有无数条直线与 平行
B. 内有两条相交直线与 平行
C. , 平行于同一条直线
D. , 垂直于同一平面
10.(2019·全国高考Ⅲ卷)如图,点 为正方形 的中心, 为正三角形,平面 平面
是线段 的中点,则
2A. ,且直线 是相交直线
B. ,且直线 是相交直线
C. ,且直线 是异面直线
D. ,且直线 是异面直线
11.(2023全国高考Ⅰ卷)在正四棱台 中, ,则该棱台的体积
为 .
12.(2023年全国高考Ⅱ卷)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为
2,高为3的正四棱锥,所得棱台的体积为 .
13.(2020·海南·高考真题)已知正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点,则三棱
1 1 1 1 1
锥A-NMD 的体积为
1
考点 02 空间几何体三视图
1.(2023·全国·乙卷)如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的
表面积为( )
A.24 B.26 C.28 D.30
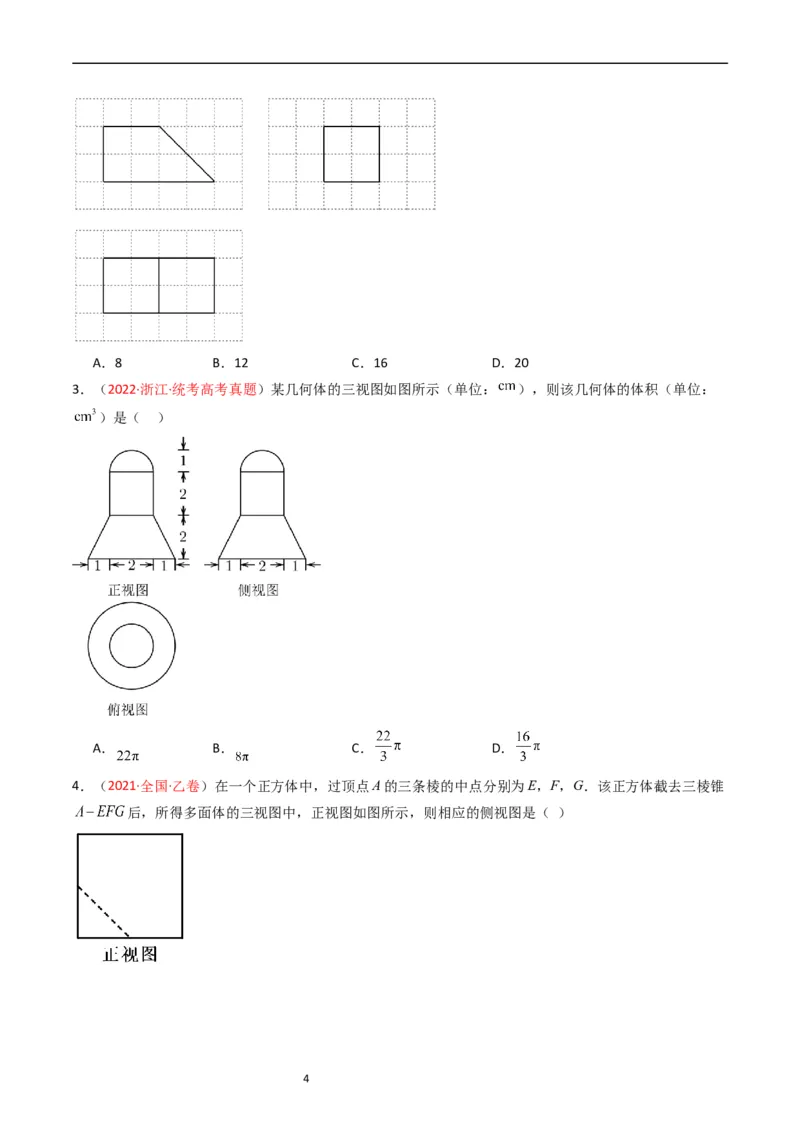
2.(2022·全国甲卷)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多
面体的体积为( )
3A.8 B.12 C.16 D.20
3.(2022·浙江·统考高考真题)某几何体的三视图如图所示(单位: ),则该几何体的体积(单位:
)是( )
A. B. C. D.
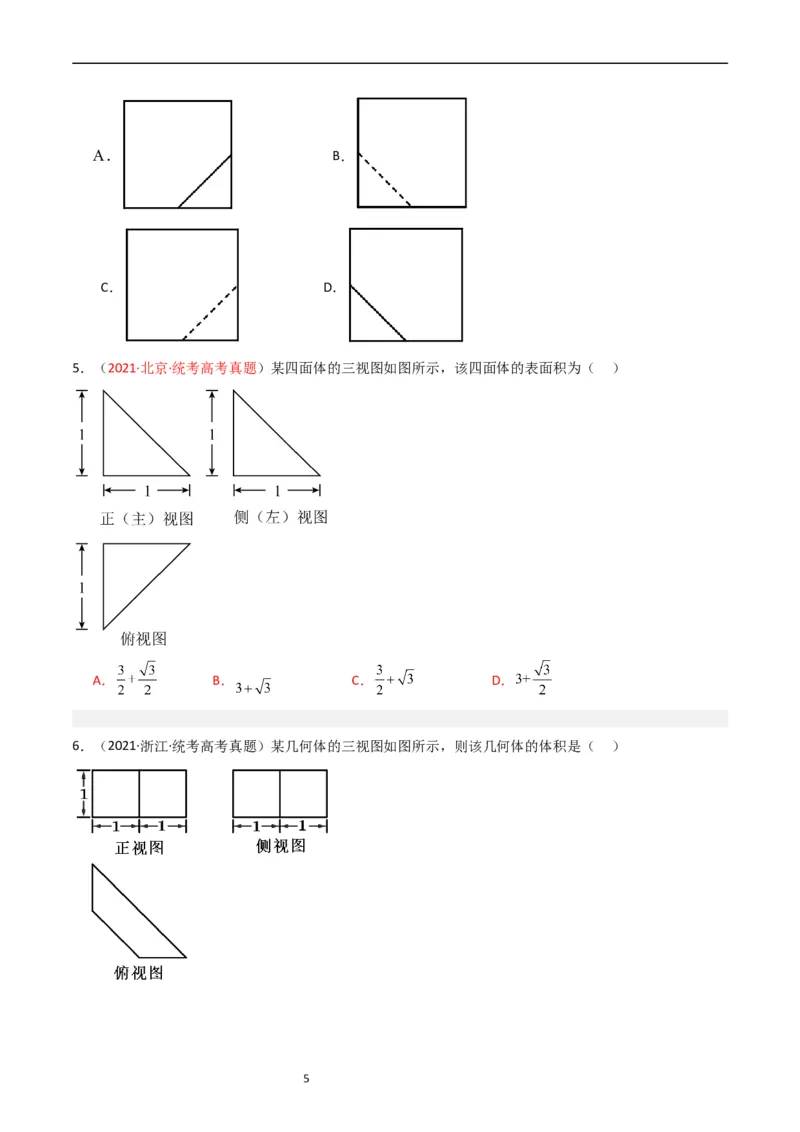
4.(2021·全国·乙卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥
后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
4A. B.
C. D.
5.(2021·北京·统考高考真题)某四面体的三视图如图所示,该四面体的表面积为( )
A. B. C. D.
6.(2021·浙江·统考高考真题)某几何体的三视图如图所示,则该几何体的体积是( )
5A. B.3 C. D.
7.(2020·全国·Ⅲ卷)下图为某几何体的三视图,则该几何体的表面积是( )
A.6+4 B.4+4 C.6+2 D.4+2
8.(2020·北京·统考高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(
).
A. B. C. D.
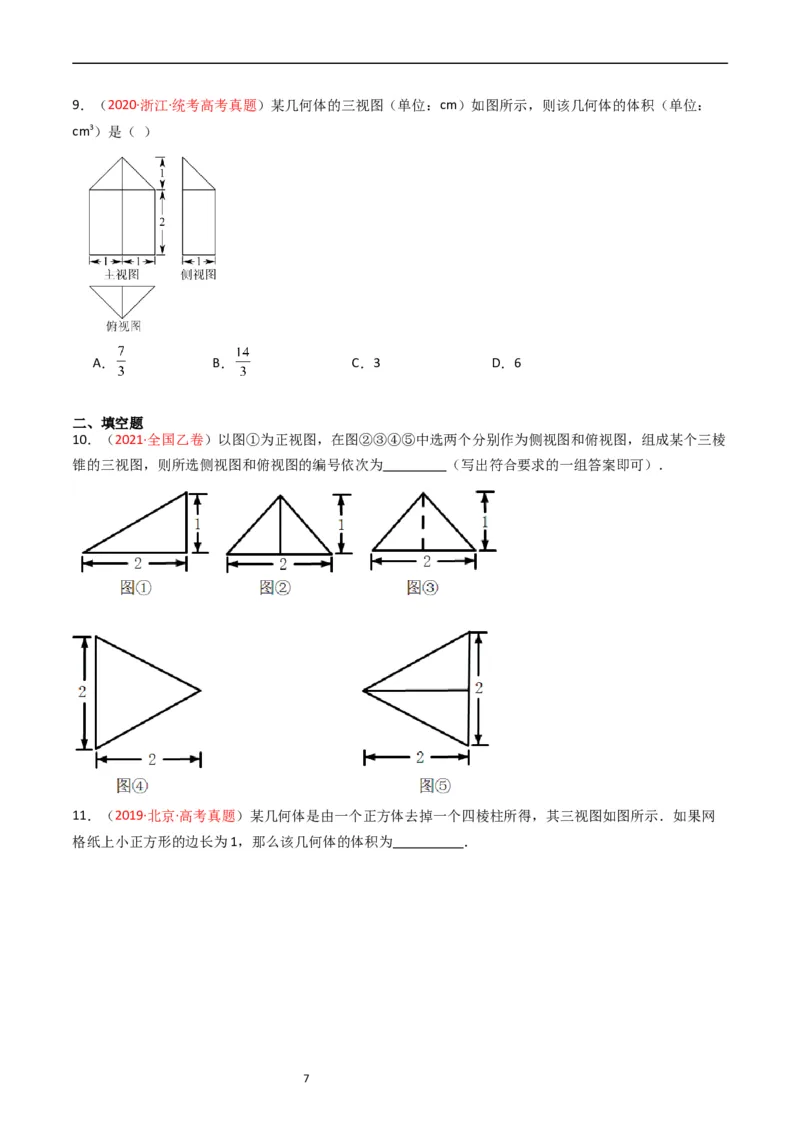
69.(2020·浙江·统考高考真题)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:
cm3)是( )
A. B. C.3 D.6
二、填空题
10.(2021·全国乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱
锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).
11.(2019·北京·高考真题)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网
格纸上小正方形的边长为1,那么该几何体的体积为 .
7考点 03 空间几何体内接球外切球问题
1.(2022·全国·乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则
当该四棱锥的体积最大时,其高为( )
A. B. C. D.
2.(2022·全国·统考高考真题)已知正三棱台的高为1,上、下底面边长分别为 和 ,其顶点都在
同一球面上,则该球的表面积为( )
A. B. C. D.
3.(2020·全国Ⅰ卷)已知 为球 的球面上的三个点,⊙ 为 的外接圆,若⊙ 的面积为
, ,则球 的表面积为( )
A. B. C. D.
4.(2020·全国·Ⅱ卷)已知△ABC是面积为 的等边三角形,且其顶点都在球O的球面上.若球O的表面
积为16π,则O到平面ABC的距离为( )
A. B. C.1 D.
二、填空题
5.(2023·全国乙卷)已知点 均在半径为2的球面上, 是边长为3的等边三角形, 平
面 ,则 .
6.(2019·全国Ⅱ卷)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正
方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或
8两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,
它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有 个面,
其棱长为 .
考点 04 空间几何题的综合应用
1.(2022·全国乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则
当该四棱锥的体积最大时,其高为( )
A. B. C. D.
2.(2022·全国·新高考Ⅰ卷)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为 ,
且 ,则该正四棱锥体积的取值范围是( )
A. B. C. D.
3.(2020·高考Ⅰ卷)已知 为球 的球面上的三个点,⊙ 为 的外接圆,若⊙ 的面积为
, ,则球 的表面积为( )
A. B. C. D.
二、填空题
4.(2023·全国·统考高考乙卷)已知点 均在半径为2的球面上, 是边长为3的等边三角形,
平面 ,则 .
5.(2023·全国·统考高考甲卷)在正方体 中, 为 的中点,若该正方体的棱
与球 的球面有公共点,则球 的半径的取值范围是 .
6.(2020·山东·统考高考真题)已知直四棱柱ABCD–A B C D 的棱长均为2,∠BAD=60°.以 为球心,
1 1 1 1
为半径的球面与侧面BCC B 的交线长为 .
1 1
7.(2019·全国高考Ⅲ卷)学生到工厂劳动实践,利用 打印技术制作模型.如图,该模型为长方体
9挖去四棱锥 后所得的几何体,其中 为长方体的中心, 分别为所在
棱的中点, , 打印所用原料密度为 ,不考虑打印损耗,制作该模型
所需原料的质量为 .
8.(2021 全国高考Ⅰ卷)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对
折,规格为 的长方形纸,对折1次共可以得到 , 两种规格的图形,它
们的面积之和 ,对折2次共可以得到 , , 三种规格的图形,
它们的面积之和 ,以此类推,则对折4次共可以得到不同规格图形的种数为 ;如果对折
次,那么 .
10