文档内容
2024年高考数学19题新模式新结构新题型
a 1,1 a 1,2 ⋯ a 1,m
a a ⋯ a
1 (2023上·北京朝阳·高三统考期中/24南通)已知A = 2,1 2,2 2,m
m ⋮ ⋮ ⋱ ⋮
a a ⋯ a
m,1 m,2 m,m
1
(m≥2)是m2个正整
数组成的m行m列的数表,当1≤i0.
所以必存在某个k既是横向有向线段的起点,又是纵向有向线段的终点,
即存在11(不妨t >t)
1 1 2 2 1 1 2 2 1 t-1 t 2 1
1
令px =xlnx,p x =1+lnx⇒px
1
在0, e
1
递减,在 ,+∞ e
1
递增,故1>t > >t>0; 2 e 1
令ht =lnt 1 +t 2 =lnt+1
tlnt
- , t-1
h't
1
=
t-1
2t-1
lnt-
2
t+1
2t-1
,令m(t)=lnt-
(t>1),
t+1
t-1
则m(t)=
2
,当t>1时,m(t)>0恒成立,故m(t)在(1,+∞)上单调递增,
t(t+1)
2t-1
可得m(t)>m(1)=0,即lnt-
>0,
t+1
故有h t
1
=
t-1
2t-1
lnt-
2
t+1
>0,
则ht 在1,+∞ 递增,
又limht
t→1
=ln2-1,limht
t→+∞
=0,故lnt 1 +t 2 ∈ln2-1,0 ,
2
故 3x + 3x =t+t ∈ ,1
1 2 1 2 e
.
【点睛】关键点点睛:本题考查求导数新定义,解题关键是将给定式子合理转化为一元函数,然后利用极限
方法求得关键函数值域,最终即可求解.
3 (合肥一中期末)同余定理是数论中的重要内容.同余的定义为:设a,b∈Z,m∈N*且m>1.若
ma-b则称a与b关于模m同余,记作a≡b(modm)(“|”为整除符号).
(1)解同余方程x2-x≡0(mod3);(2)设(1)中方程的所有正根构成数列a
n
4
,其中a0(n=1,2,3,⋯),是否存在正实数M,使得对任意的正整数n,都有a ≤M?如果存在,写出一个
n n
满足条件的M;如果不存在,说明理由.
【答案】(1){1,3,5}
(2)证明见解析 (3)不存在,理由见解析
【解析】
【分析】(1)根据定义知a ≥0,讨论a >2、a <2及a ,a 大小求所有a 可能值;
n 3 3 3 4 4
(2)由a ≥0,假设存在n ∈N*使a ≤a ,进而有a ≤max{a ,a }≤a ,可得min{a ,a }=0,即
n 0 n n0 n0 n0+1 n0+2 n0 n0+1 n0+2可证结论;
(3)由题设a ≠a (n=2,3,⋯),令S={n|a >a ,n≥1},讨论S=∅、S≠∅求证a >M即可判断存在
n n+1 n n+1 n
性.
【小问1详解】
由a =maxa ,a
n n+1 n+2
8
-mina ,a
n+1 n+2
≥0,a=max{2,a }-min{2,a }=1,
1 3 3
若a >2,则a -2=1,即a =3,此时a =max{3,a }-min{3,a }=2,
3 3 3 2 4 4
当a >3,则a -3=2,即a =5;
4 4 4
当a <3,则3-a =2,即a =1;
4 4 4
若a <2,则2-a =1,即a =1,此时a =max{1,a }-min{1,a }=2,
3 3 3 2 4 4
当a >1,则a -1=2,即a =3;
4 4 4
当a <1,则1-a =2,即a =-1(舍);
4 4 4
综上,a 的所有可能值为{1,3,5}.
4
【小问2详解】
由(1)知:a ≥0,则mina ,a
n n+1 n+2
≥0,
数列a
n
中的项存在最大值,故存在n ∈N*使a ≤a ,(n=1,2,3,⋯),
0 n n0
由a =max{a ,a }-min{a ,a }≤max{a ,a }≤a ,
n0 n0+1 n0+2 n0+1 n0+2 n0+1 n0+2 n0
所以min{a ,a }=0,故存在k∈{n +1,n +2}使a =0,
n0+1 n0+2 0 0 k
所以0为数列a
n
中的项;
【小问3详解】
不存在,理由如下:由a >0(n=1,2,3,⋯),则a ≠a (n=2,3,⋯),
n n n+1
设S={n|a >a ,n≥1},
n n+1
若S=∅,则a≤a ,a0,取n
1
=
a
1
+2([x]表示不超过x的最大整数),
当n>n 时,a =(a -a )+(a -a )+...+(a -a )+a
1 n n n-1 n-1 n-2 3 2 2
=a +a +...+a+a ≥(n-1)a>M;
n-2 n-3 1 2 1
若S≠∅,则S为有限集,
设m=max{n|a >a ,n≥1},a 0,取n
2
=
a
m+1
+m+1([x]表示不超过x的最大整数),
当n>n 时,a =(a -a )+(a -a )+...+(a -a )+a
2 n n n-1 n-1 n-2 m+2 m+1 m+1
=a +a +...+a +a ≥(n-m)a >M;
n-2 n-3 m m+1 m+1
综上,不存在正实数M,使得对任意的正整数n,都有a ≤M.
n
【点睛】关键点点睛:第三问,首选确定a ≠a (n=2,3,⋯),并构造集合S={n|a >a ,n≥1},讨论S=
n n+1 n n+1
∅、S≠∅研究存在性.
8 (高考仿真)若项数为k(k∈N*,k≥3)的有穷数列{a }满足:0≤aa +a =a ,所以a +a∉a
k-1 i k-1 2 k k-1 i n
,
由0=a -a 0,λ≠1),
λ是一个常数,那么动点M的轨迹就是阿波罗尼斯圆,圆心在直线PQ上.已知动点M的轨迹是阿波罗尼斯
x2 y2
圆,其方程为x2+y2=4,定点分别为椭圆C: + =1(a>b>0)的右焦点F与右顶点A,且椭圆C的离
a2 b2
1
心率为e= .
2(1)求椭圆C的标准方程;
(2)如图,过右焦点F斜率为k(k>0)的直线l与椭圆C相交于B,D(点B在x轴上方),点S,T是椭圆C上
异于B,D的两点,SF平分∠BSD,TF平分∠BTD.
BS
①求
10
DS
的取值范围;
81π
②将点S、F、T看作一个阿波罗尼斯圆上的三点,若△SFT外接圆的面积为 ,求直线l的方程.
8
x2 y2 1
【答案】(1) + =1(2)① ,1
8 6 3
5 10
②y= x-
2 2
【解析】(1)方法①特殊值法,令M±2,0
c-2
,
a-2
c+2
= ,且a=2c,解得c2=2.
a+2
x2 y2
∴a2=8,b2=a2-c2=6,椭圆C的方程为 + =1,
8 6
方法②设Mx,y
MF
,由题意
MA
(x-c)2+y2
= =λ(常数),整理得:
(x-a)2+y2
x2+y2+ 2c-2aλ2 x+ λ2a2-c2 =0,故 2c λ - 2- 2 1 aλ2 =0 ,又 c = 1 ,解得:a=2 2,c= 2.
λ2-1 λ2-1 λ2a2-c2 =-4 a 2
λ2-1
x2 y2
∴b2=a2-c2=6,椭圆C的方程为 + =1.
8 6
S 1 SB (2)①由 △SBF = 2
S △SDF
⋅SF ⋅sin∠BSF
1 SD
2
⋅SF
SB =
⋅sin∠DSF
SD
S BF ,又 △SBF =
S △SDF
DF
,
BS
∴
DS
BF
=
DF
BF
(或由角平分线定理得),令
DF
=λ,则BF=λFD,设Dx 0 ,y 0 ,
则有3x2 0 +4y2 0 =24,又直线l的斜率k>0,则x 0 ∈-2 2, 2 x = 2λ+1 , B -λx 0 y =-λy
B 0
代入3x2+4y2-24=0得:3 21+λ -λx 0 2+4λ2y2 0 -24=0,即λ+1 5λ-3- 2λx 0 =0,
3 1
∵λ>0,∴λ= ∈ ,1
5- 2x 3
0
.
SB
②由(1)知,
SD
TB
=
TD
BF
=
DF
,由阿波罗尼斯圆定义知,
S,T,F在以B,D为定点的阿波罗尼斯圆上,设该圆圆心为C ,半径为r,与直线l的另一个交点为N,则有
1
BF
DF
NB
=
ND
BF
,即
DF
2r-BF
=
2r+DF
1
,解得:r=
1
BF
- 1
DF
.
81 9 1
又S =πr2= π,故r= ,∴
圆C1 8 2 2 BF
1
-
DF
2 2
=
9又DF
11
= x 0 - 2 2+y2 0 = x 0 - 2
3 1
2+6- x2=2 2- x , 4 0 2 0
1
∴
BF
1
-
DF
1
=
λDF
1
-
DF
5- 2x
= 0
32 2- 1x
2 0
1 2- 2x
- = 0
2 2- 1x 32 2- 1x
2 0 2 0
2 2
= .
9
解得:x =- 2 ,y =- 6- 3 x2=- 3 10 ,∴k= -y 0 = 5 ,∴直线l的方程为y= 5 x- 10 .
0 2 0 4 0 4 2-x 2 2 2
0
10 (郑州外国语)记U={1,2,⋯,100}.对数列a
n
n∈N* 和U的子集T,若T=∅,定义S =0;若
T
T=t,t ,⋯,t
1 2 k
,定义S =a +a +⋯+a .例如:T=1,3,66
T t1 t2 tk
时,S =a+a +a .现设a
T 1 3 66 n
n∈N*
是公比为3的等比数列,且当T=2,4 时,S =30.
T
(1)求数列a
n
的通项公式;
(2)对任意正整数k1≤k≤100 ,若T1,2,⋯,k ,求证:S 2S .
B 1 2 m 2 2 2 2 A B
综上所述,S ≥2S ,因此S +S ≥2S .
A B C C∩D D
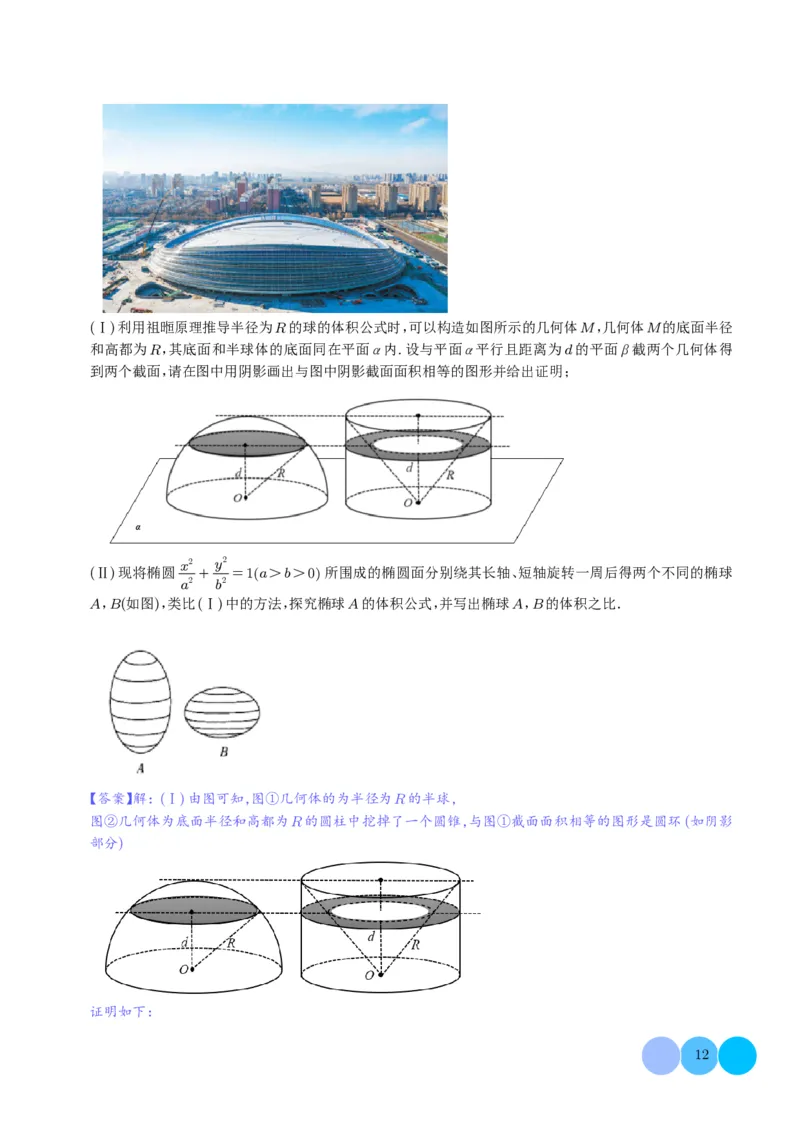
11 (福建模拟)2022年北京冬奥会标志性场馆--国家速滑馆的设计理念来源于一个冰和速度结合的
创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣
的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆
形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、
椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研
究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导
球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲
之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公
式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.(Ⅰ)利用祖暅原理推导半径为R的球的体积公式时,可以构造如图所示的几何体M,几何体M的底面半径
和高都为R,其底面和半球体的底面同在平面α内.设与平面α平行且距离为d的平面β截两个几何体得
到两个截面,请在图中用阴影画出与图中阴影截面面积相等的图形并给出证明;
x2 y2
(Ⅱ)现将椭圆 + =1a>b>0
a2 b2
12
所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球
A,B(如图),类比(Ⅰ)中的方法,探究椭球A的体积公式,并写出椭球A,B的体积之比.
【答案】解: (Ⅰ)由图可知,图①几何体的为半径为R的半球,
图②几何体为底面半径和高都为R的圆柱中挖掉了一个圆锥,与图①截面面积相等的图形是圆环(如阴影
部分)
证明如下:在图①中,设截面圆的圆心为O 1 ,易得截面圆O 1 的面积为πR2-d2
13
,
在图②中,截面截圆锥得到的小圆的半径为d,所以,圆环的面积为πR2-d2 ,
所以,截得的截面的面积相等
(Ⅱ)类比(Ⅰ)可知,椭圆的长半轴为a,短半轴为b,
构造一个底面半径为b,高为a的圆柱,把半椭球与圆柱放在同一个平面上(如图),
在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,即挖去的圆锥底面半径为b,高为
a;
b2
在半椭球截面圆的面积π a2-d2
a2
,
b2 b2
在圆柱内圆环的面积为πb2-π d2=π a2-d2
a2 a2
∴距离平面α为d的平面截取两个几何体的平面面积相等,
根据祖暅原理得出椭球A的体积为:
V=2V -V
A 圆柱 圆锥
1
=2π⋅b2⋅a- π⋅b2⋅a
3
4π
= ab2,
3
4π
同理:椭球B的体积为V= a2b
B 3
b
所以,两个椭球A,B的体积之比为 .
a
【解析】本题考查新定义问题,解题的关键是读懂题意,构建圆柱,通过计算得到高相等时截面面积相等,考
查学生的空间想象能力与运算求解能力,属于中档题.
(Ⅰ)由题意,直接画出阴影即可,然后分别求出图①中圆的面积及图②中圆环的面积即可证明;
(Ⅱ)类比(Ⅰ)可知,椭圆的长半轴为a,短半轴为b,构造一个底面半径为b,高为a的圆柱,把半椭球与圆柱
放在同一个平面上,在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,即挖去的圆
锥底面半径为b,高为a,证明截面面积相等,由祖暅原理求出出椭球A的体积,同理求出椭球B的体积,作
比得出答案.
12 用数学的眼光看世界就能发现很多数学之“美”.现代建筑讲究线条感,曲线之美让人称奇.衡量曲
线弯曲程度的重要指标是曲率,曲线的曲率定义如下:若f'x 是fx 的导函数,f''x 是f'x 的导函数,
则曲线y=fx 在点 x,fx
|f(x)|
处的曲率K=
1+[f (x)]2
.
3
2(1)若曲线fx
14
=lnx+x与gx = x在1,1 处的曲率分别为K ,K ,比较K ,K 的大小; 1 2 1 2
(2)求正弦曲线hx =sinx(x∈R)曲率的平方K2的最大值.
1 1 1 -1 1 -3
【答案】解:(1)由题意,得f'(x)= +1,f''(x)=- ,g'(x)= x 2,g''(x)=- x 2,
x x2 2 4
f''(1) ∴K=
1 1+f'(1) 2
-1 =
3 2 1+22
1 g''(1) = ,K =
3 125 2 2 1+g'(1) 2
-1
4 =
3 2 1+ 1 2 2
1
= 4 = 2 ,
3 125 125 2 64
∴K