文档内容
2024年高考数学19题新模式新结构新题型
a 1,1 a 1,2 ⋯ a 1,m
a a ⋯ a
1 (2023上·北京朝阳·高三统考期中/24南通)已知A = 2,1 2,2 2,m
m ⋮ ⋮ ⋱ ⋮
a a ⋯ a
m,1 m,2 m,m
1
(m≥2)是m2个正整
数组成的m行m列的数表,当1≤i1.
若ma-b则称a与b关于模m同余,记作a≡b(modm)(“|”为整除符号).
(1)解同余方程x2-x≡0(mod3);
(2)设(1)中方程的所有正根构成数列a
n
3
,其中a0(n=1,2,3,⋯),是否存在正实数M,使得对任意的正整数n,都有a ≤M?如果存在,写出一个
n n
满足条件的M;如果不存在,说明理由.8 (高考仿真)若项数为k(k∈N*,k≥3)的有穷数列{a }满足:0≤a0,λ≠1),
λ是一个常数,那么动点M的轨迹就是阿波罗尼斯圆,圆心在直线PQ上.已知动点M的轨迹是阿波罗尼斯
x2 y2
圆,其方程为x2+y2=4,定点分别为椭圆C: + =1(a>b>0)的右焦点F与右顶点A,且椭圆C的离
a2 b2
1
心率为e= .
2
(1)求椭圆C的标准方程;
(2)如图,过右焦点F斜率为k(k>0)的直线l与椭圆C相交于B,D(点B在x轴上方),点S,T是椭圆C上
异于B,D的两点,SF平分∠BSD,TF平分∠BTD.
BS
①求
DS
的取值范围;
81π
②将点S、F、T看作一个阿波罗尼斯圆上的三点,若△SFT外接圆的面积为 ,求直线l的方程.
810 (郑州外国语)记U={1,2,⋯,100}.对数列a
n
8
n∈N* 和U的子集T,若T=∅,定义S =0;若
T
T=t,t ,⋯,t
1 2 k
,定义S =a +a +⋯+a .例如:T=1,3,66
T t1 t2 tk
时,S =a+a +a .现设a
T 1 3 66 n
n∈N*
是公比为3的等比数列,且当T=2,4 时,S =30.
T
(1)求数列a
n
的通项公式;
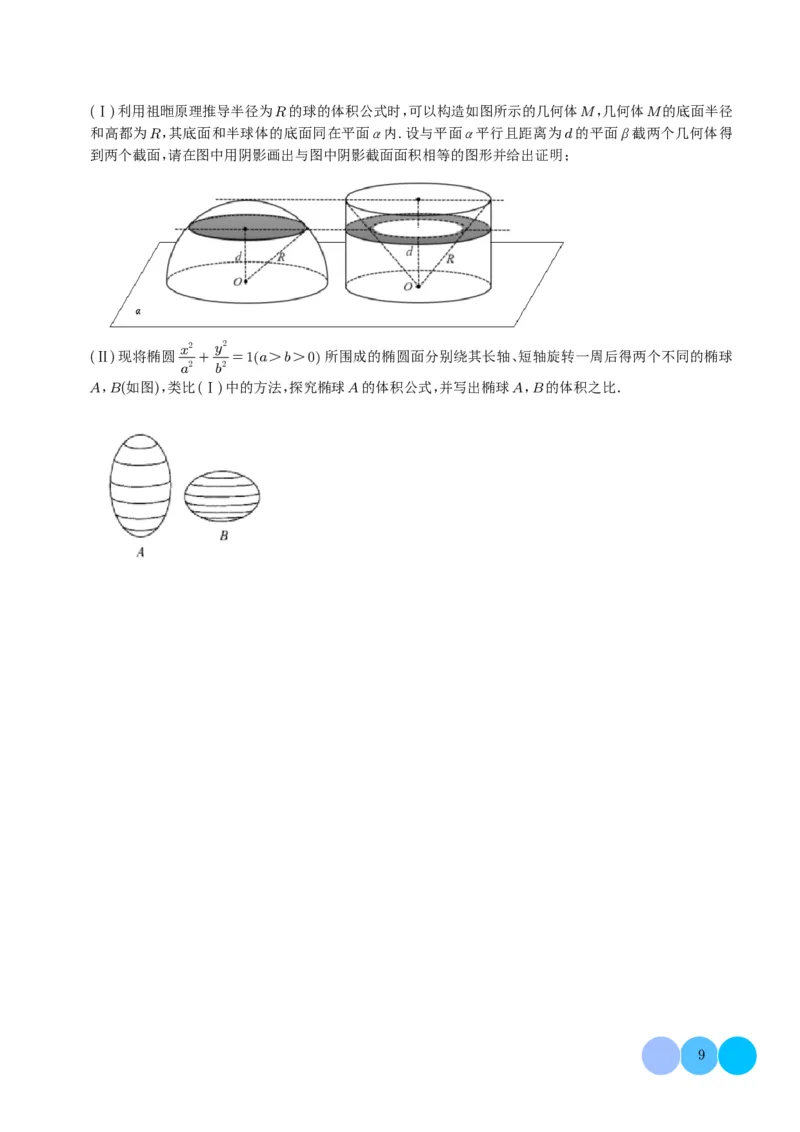
(2)对任意正整数k1≤k≤100 ,若T1,2,⋯,k ,求证:S b>0
a2 b2
9
所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球
A,B(如图),类比(Ⅰ)中的方法,探究椭球A的体积公式,并写出椭球A,B的体积之比.12 用数学的眼光看世界就能发现很多数学之“美”.现代建筑讲究线条感,曲线之美让人称奇.衡量曲
线弯曲程度的重要指标是曲率,曲线的曲率定义如下:若f'x
10
是fx 的导函数,f''x 是f'x 的导函数,
则曲线y=fx 在点 x,fx
|f(x)|
处的曲率K=
1+[f (x)]2
.
3
2
(1)若曲线fx =lnx+x与gx = x在1,1 处的曲率分别为K ,K ,比较K ,K 的大小; 1 2 1 2
(2)求正弦曲线hx =sinx(x∈R)曲率的平方K2的最大值.1
13 设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为1- (∠QPQ +∠Q PQ
2π 1 2 2 3
+⋯+∠Q PQ +∠Q PQ),其中Q(i=1,2,⋯,k,k≥3)为多面体M的所有与点P相邻的顶点,且平
k-1 k k 1 i
面Q PQ ,平面Q PQ ,⋯,平面Q PQ 和平面Q PQ 遍历多面体M的所有以P为公共点的面.
1 2 2 3 k -1 k k 1
(1)任取正四面体的一个顶点,求该点处的离散曲率;
2
(2)如图1,已知长方体A B C D -ABCD,AB=BC=1,AA = ,点P为底面A B C D 内的一
1 1 1 1 1 2 1 1 1 1
个动点,则求四棱锥P-A BC D 在 点 P处的离散曲率的最小值;
(3)图2为对某个女孩面部识别过程中的三角剖分结果,所谓三角剖分,就是先在面部取若干采样点,然后
用短小的直线段连接相邻三个采样点形成三角形网格.区域α和区域β中点的离散曲率的平均值更大的
是哪个区域?(只需确定“区域α”还是“区域β”)
1114 近些年来,三维扫描技术得到空前发展,从而催生了数字几何这一新兴学科.数字几何是传统几何
和计算机科学相结合的产物.数字几何中的一个重要概念是曲率,用曲率来刻画几何体的弯曲程度.规定:
多面体在顶点处的曲率等于2π与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的
多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等
π
于该多面体各顶点的曲率之和.例如:正方体在每个顶点有3个面角,每个面角是 ,所以正方体在各顶点
2
π π
的曲率为2π-3× = ,故其总曲率为4π.
2 2
(1)求四棱锥的总曲率;
(2)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多
面体的顶点数为D,棱数为L,面数为M,则有:D-L+M=2.利用此定理试证明:简单多面体的总曲率是
常数.
12