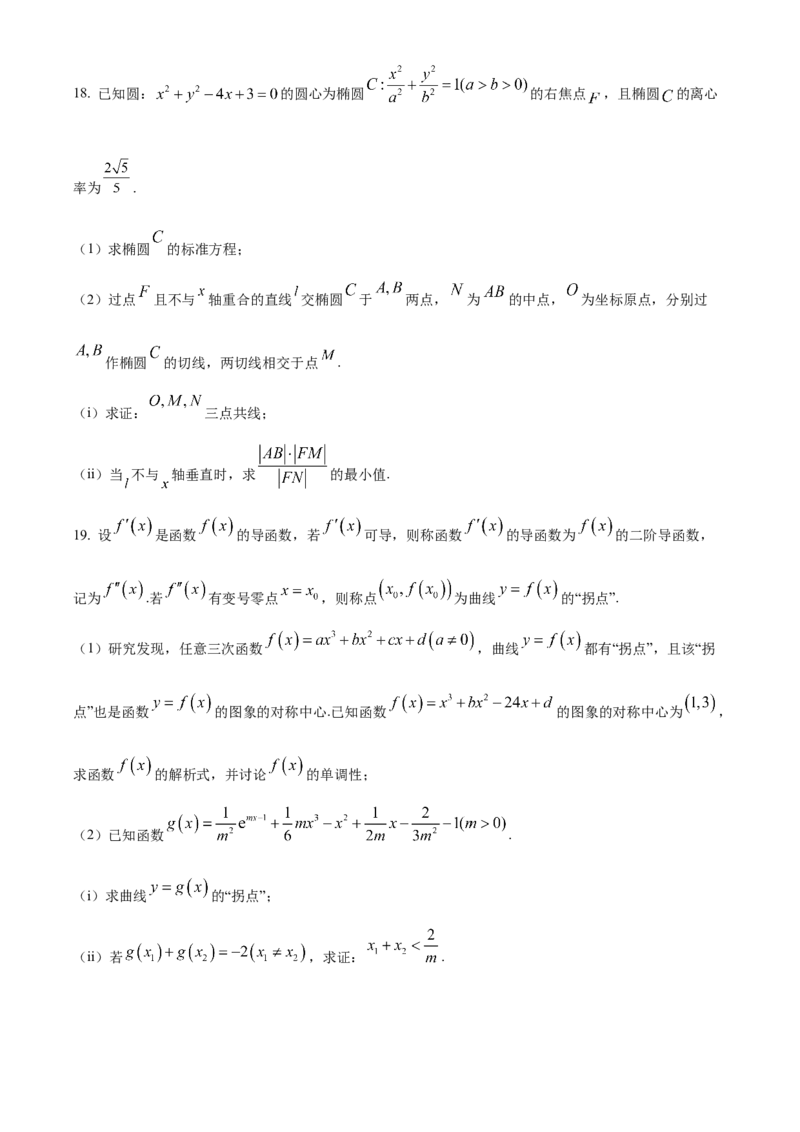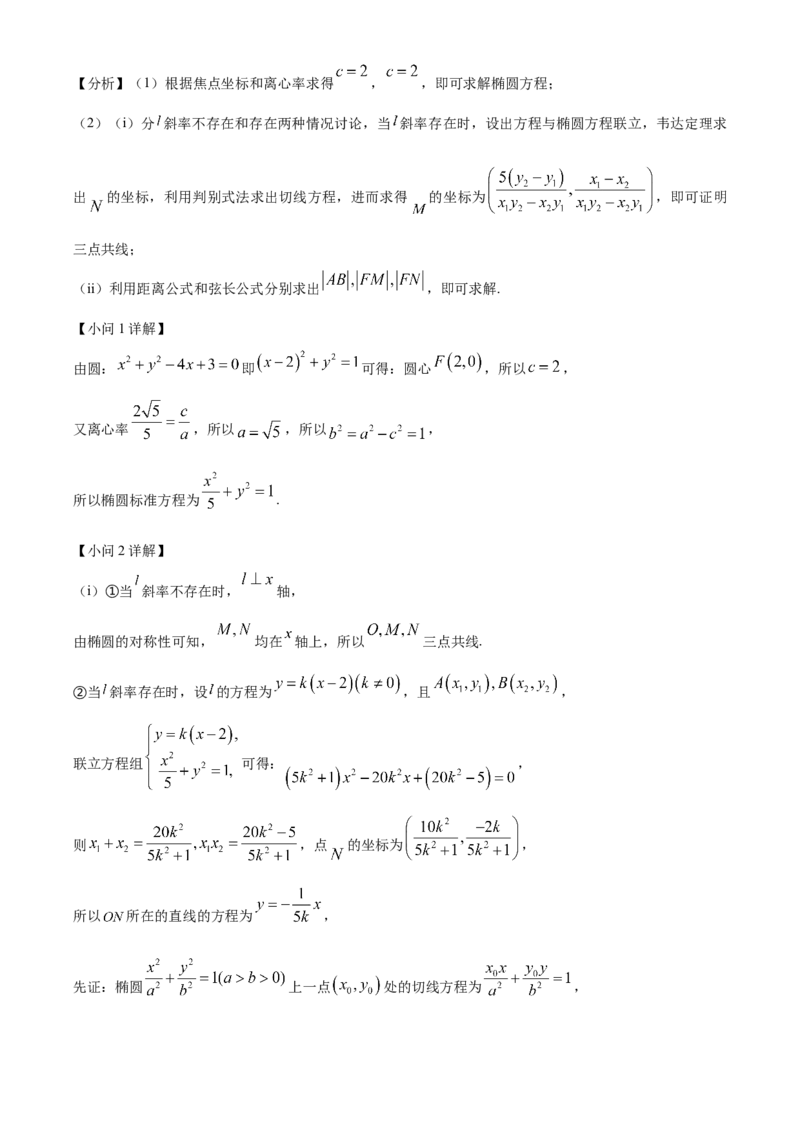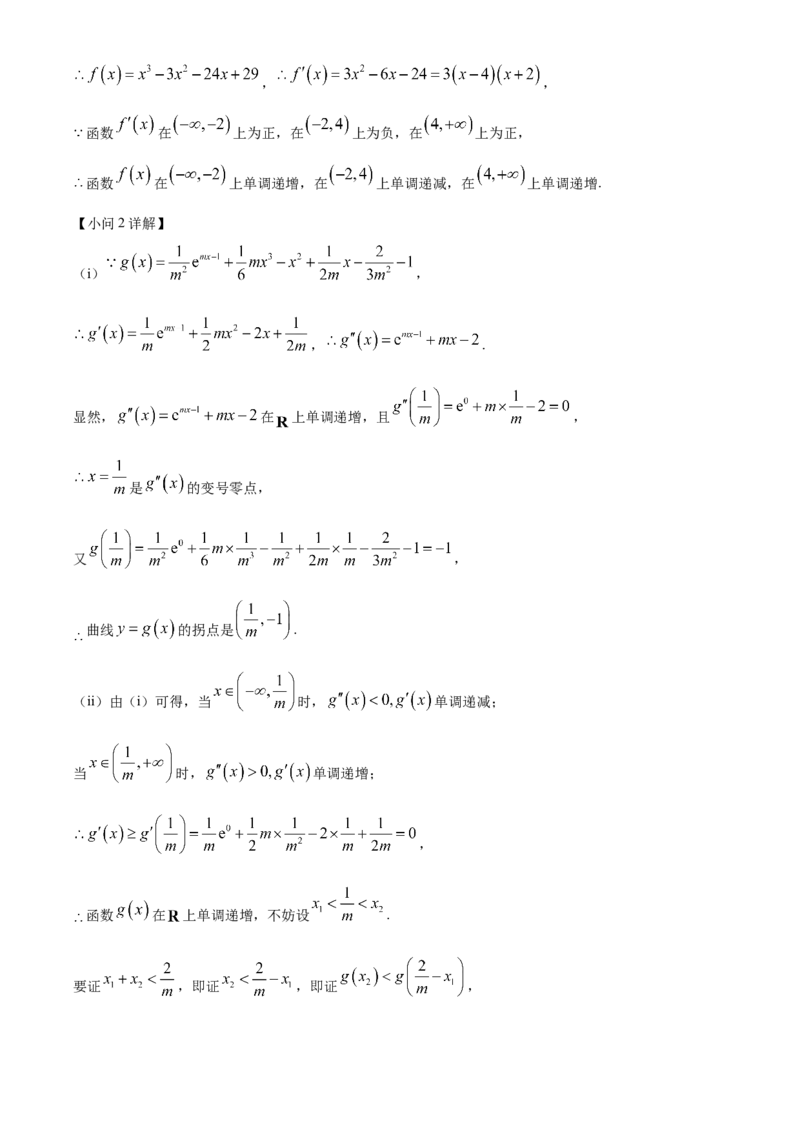文档内容
高二数学试卷
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷第1页至第2页,第Ⅱ卷第3
页至第4页.考试结束后,请将答题卡交回.满分150分,考试用时120分钟.
第I卷(选择题,共58分)
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清
楚,
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干
净后,再选涂其他答案标号.在试题卷上作答无效
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1. 已知命题 ,则命题 的否定是( )
A. B.
C. D.
2. 曲线 在 处切线 倾斜角为( )
的
A. 0 B. C. D.
3. 我国古代数学著作《九章算术》中有如下问题:“今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我
羊食半马.”马主曰:“我马食半牛.”问:“马主出几何?”意思是“现有羊、马、牛三畜,吃了人家田里的禾苗,
禾苗主人要求三位主人共赔偿5斗粟.羊主人说:“我的羊所吃禾苗数是马吃的一半,”马主人说:“我的马
所吃数是牛吃的一半.”问马主人应赔偿多少更合理?( )
.
A 斗 B. 斗 C. 斗 D. 斗4. 的展开式中 的系数是( )
.
A 48 B. -48 C. 72 D. -72
5. 小王去秦始皇兵马俑博物馆游玩,买了8个不同的兵马俑纪念品,其中将军俑3个,骑兵俑3个,跪射
俑2个,将这8个纪念品排成一排,要求同种类型相邻,则不同的排法共有( )种.
A. 48 B. 72 C. 216 D. 432
6. 已知在 中,角 所对的边分别为 .内角 为等差数列,若 边上的中线长为
,且 的面积为 ,则 的值为( )
A. 2 B. 3 C. 4 D. 5
的
7. 已知点 在函数 图象上,点 在直线 上,记 ,则(
)
A. 当 取最小值时,点 的横坐标为
B. 当 取最小时,点 的横坐标为1
C. 当 取最小值时,点 的横坐标为
D. 当 取最小时,点 的横坐标为
8. 已知 ,则( )
A. B.
C. D.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项是
符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 下列说法正确的是( )
A. 设已知随机变量 满足 ,则B. 若 ,则
C. 若 ,设 ,则
D. 若事件 相互独立且 ,则
10. 已知函数 ,下列说法中正确的是( )
A. 对于任意 ,函数 在定义域上是单调递减函数
B. 对于任意 ,函数 存在最小值
C. 存在 ,使得对于任意 都有 恒成立
D. 存在 ,使得 在定义域上有两个零点
11. 已知 为两个随机事件, 分别为其对立事件,则下列说法正确的是( )
A. 若 ,则
B. 若 ,则
C. 若 ,则
D. 若 ,则
第II卷(非选择题,共92分)
注意事项:
第II卷用黑色碳素笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.
三、填空题(本大题共3小题,每小题5分,共15分)
12. 某社团有3名女生、4名男生,随机选3名同学出来参加某个活动,用 表示选到男生的人数,则
的概率是__________.13. 若 ,则 ______.(用数字作
答)
14. 已知定义在 上的函数 满足: ,则不等式
的解集为__________.
四、解答题(共77分.解答应写出文字说明,证明过程或演算步骤)
15. 在某次数学竞赛的初赛中,参赛选手需要从4道“圆锥曲线”和3道“函数与导数”共7道不同的试题中依
次抽取2道进行作答,抽出的题目不再放回.
(1)求选手甲第1次抽到“圆锥曲线”试题且第2次抽到“函数与导数”试题的概率;
(2)求选手甲第2次抽到“函数与导数”试题的概率;
(3)求选手甲第2次抽到“函数与导数”试题的条件下,第1次抽到“圆锥曲线”试题的概率.
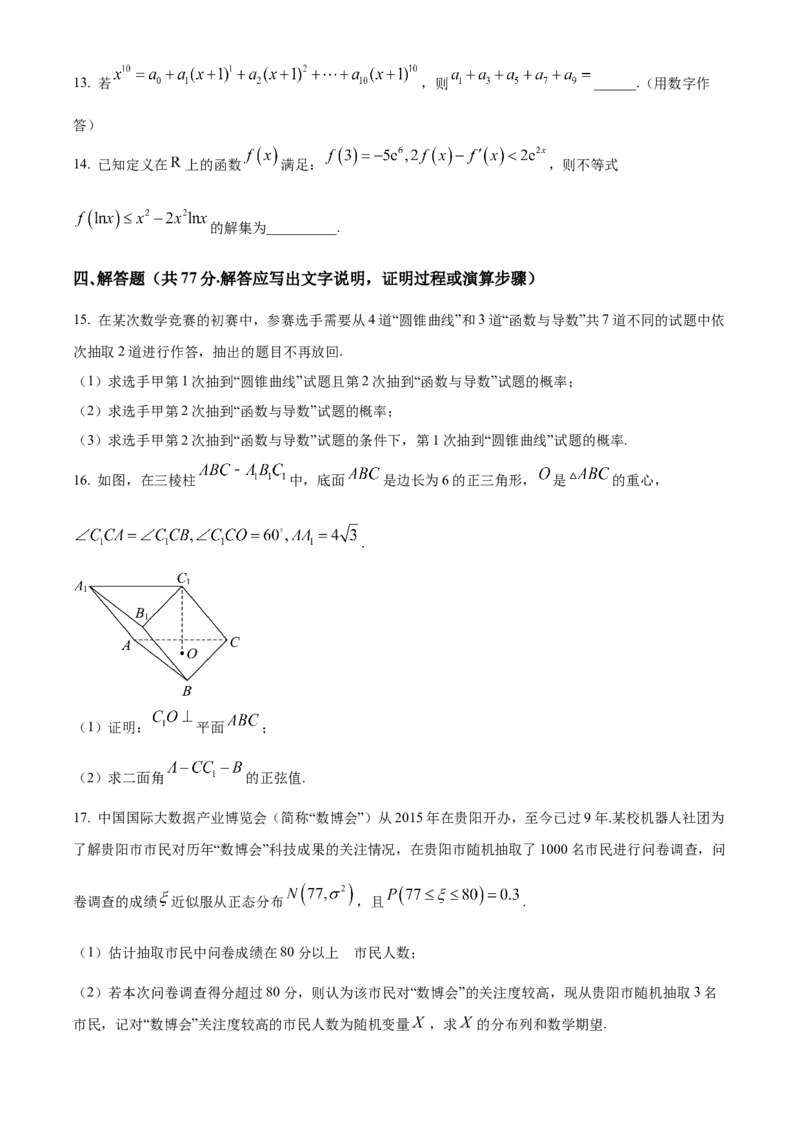
16. 如图,在三棱柱 中,底面 是边长为6的正三角形, 是 的重心,
.
(1)证明: 平面 ;
(2)求二面角 的正弦值.
17. 中国国际大数据产业博览会(简称“数博会”)从2015年在贵阳开办,至今已过9年.某校机器人社团为
了解贵阳市市民对历年“数博会”科技成果的关注情况,在贵阳市随机抽取了1000名市民进行问卷调查,问
卷调查的成绩 近似服从正态分布 ,且 .
的
(1)估计抽取市民中问卷成绩在80分以上 市民人数;
(2)若本次问卷调查得分超过80分,则认为该市民对“数博会”的关注度较高,现从贵阳市随机抽取3名
市民,记对“数博会”关注度较高的市民人数为随机变量 ,求 的分布列和数学期望.18. 已知圆: 的圆心为椭圆 的右焦点 ,且椭圆 的离心
率为 .
(1)求椭圆 的标准方程;
(2)过点 且不与 轴重合的直线 交椭圆 于 两点, 为 的中点, 为坐标原点,分别过
作椭圆 的切线,两切线相交于点 .
(i)求证: 三点共线;
(ii)当 不与 轴垂直时,求 的最小值.
19. 设 是函数 的导函数,若 可导,则称函数 的导函数为 的二阶导函数,
记为 .若 有变号零点 ,则称点 为曲线 的“拐点”.
(1)研究发现,任意三次函数 ,曲线 都有“拐点”,且该“拐
点”也是函数 的图象的对称中心.已知函数 的图象的对称中心为 ,
求函数 的解析式,并讨论 的单调性;
(2)已知函数 .
(i)求曲线 的“拐点”;
(ii)若 ,求证: .高二数学试卷
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷第1页至第2页,第Ⅱ卷第3
页至第4页.考试结束后,请将答题卡交回.满分150分,考试用时120分钟.
第I卷(选择题,共58分)
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清
楚,
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干
净后,再选涂其他答案标号.在试题卷上作答无效
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1. 已知命题 ,则命题 的否定是( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据全称命题与存在性命题的关系,准确改写,即可求解.
【详解】由题意,根据全称命题与存在性命题的关系,可得:
命题 的否定是 .
故选:B.
2. 曲线 在 处切线的倾斜角为( )A. 0 B. C. D.
【答案】D
【解析】
【分析】利用导数的几何意义求解.
【详解】解:因为 ,
所以曲线在 处的切线的斜率为 ,
结合直线倾斜角范围及斜率与倾斜角关系知:切线倾斜角为 ,
故选:D.
3. 我国古代数学著作《九章算术》中有如下问题:“今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我
羊食半马.”马主曰:“我马食半牛.”问:“马主出几何?”意思是“现有羊、马、牛三畜,吃了人家田里的禾苗,
禾苗主人要求三位主人共赔偿5斗粟.羊主人说:“我的羊所吃禾苗数是马吃的一半,”马主人说:“我的马
所吃数是牛吃的一半.”问马主人应赔偿多少更合理?( )
A. 斗 B. 斗 C. 斗 D. 斗
【答案】C
【解析】
【分析】设羊主人应赔偿 斗,则马主人应赔偿 斗,牛主人应赔偿 斗,根据题意,列出方程,即
可求解.
【详解】设羊主人应赔偿 斗,则马主人应赔偿 斗,牛主人应赔偿 斗,
由题意得 ,所以 ,所以马主人应赔偿 斗.
故选:C.
4. 的展开式中 的系数是( )
A. 48 B. -48 C. 72 D. -72
【答案】A【解析】
【分析】根据题意,利用二项式定理得展开式,结合多项式展开式的形式,即可求解.
【详解】由题意,多项式 的展开式中, 的系数等于 .
故选:A.
5. 小王去秦始皇兵马俑博物馆游玩,买了8个不同的兵马俑纪念品,其中将军俑3个,骑兵俑3个,跪射
俑2个,将这8个纪念品排成一排,要求同种类型相邻,则不同的排法共有( )种.
A. 48 B. 72 C. 216 D. 432
【答案】D
【解析】
【分析】利用相邻问题中的捆绑法可求出结果.
【详解】先将 个将军俑捆在一起当一个元素使用,有 种捆法,
将 个骑兵俑捆在一起当一个元素使用,有 种捆法,
将 个跪射俑捆在一起当一个元素使用,有 种捆法,
再将所得 个元素作全排,有 种排法,所以不同的排法共有 种.
故选:D.
6. 已知在 中,角 所对的边分别为 .内角 为等差数列,若 边上的中线长为
,且 的面积为 ,则 的值为( )
A. 2 B. 3 C. 4 D. 5
【答案】A
【解析】
【分析】首先求出B,根据平行四边形法则得 ,两边平方得到一个关于 , 的方程,
再根据面积公式得到 , 的另一个方程,最后由余弦定理计算出 .
【详解】因为内角 成等差数列,所以 ,即 ,
设 中点为 ,所以 ,由题意, ,所以 ,即 ,
又因为 ,所以 , ,
由余弦定理, ,所以 .
故选:A.
7. 已知点 在函数 的图象上,点 在直线 上,记 ,则(
)
A. 当 取最小值时,点 的横坐标为
B. 当 取最小时,点 的横坐标为1
C. 当 取最小值时,点 的横坐标为
D. 当 取最小时,点 的横坐标为
【答案】D
【解析】
【分析】利用导数研究函数 的单调性,作出函数的图象,然后利用数形结合知函数
在 点处的切线平行于直线 ,然后利用导数的几何意义求得切点坐标,再利用垂直
关系求得直线PQ方程,与直线 联立求解交点即可.
【详解】 ,则 ,令 得 ,
令 得 ,所以函数 在 上单调递增,在 上单调递减,
作出函数函数 的图象,
如图:由题意,当 最小时,函数 在 点处的切线平行于直线 ,
过 点作直线 的垂线,垂足即为点 .设 的坐标为 ,
因为 ,所以 ,解得 ,即 点的坐标为 ,
所以过 点,且与直线 垂直的直线方程为 ,
联立方程 解得 的坐标为 .
故选:D.
8. 已知 ,则( )
A. B.
C. D.
【答案】C
【解析】
【分析】令函数 ,利用导数求得函数 在 上单调递增,结合对数的运算性质和函数
的单调性,即可求解.
【详解】令函数 ,可得 ,所以函数 在 上单调递增,又因为 ,
因为 ,所以 ,即 .
故选:C.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项是
符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 下列说法正确的是( )
A. 设已知随机变量 满足 ,则
B. 若 ,则
C. 若 ,设 ,则
D. 若事件 相互独立且 ,则
【答案】ACD
【解析】
【分析】根据期望的性质,可判定A正确;结合二项分布方差的公式,可判定B错误;根据正态分布曲线
的对称性,可得判定C正确;根据条件概率的计算公式,可判定D正确.
【详解】对于A中,由 ,所以 ,所以A正确;
对于B中,由 ,所以 ,所以B错误;
对于C中,由 ,所以 ,所以C正确;
对于D中,因为 相互独立,所以 ,且 ,所以D正确.
故选:ACD.
10. 已知函数 ,下列说法中正确的是( )
A. 对于任意 ,函数 在定义域上是单调递减函数
B. 对于任意 ,函数 存在最小值
C. 存在 ,使得对于任意 都有 恒成立
D. 存在 ,使得 在定义域上有两个零点
【答案】BD
【解析】
【分析】A.利用导数法判断;C.由 时, 判断;B.利用导数法判断;D.利用导数
法判断.
【详解】因为 ,所以 .
当 时, ,函数 在 上单调递增,A错误;
又因为当 时, ,C错误;
当 时,显然 在 上单调递增,且当 时, ,当 时,
,
所以存在 ,使得函数 在 上单调递减,在 上单调递增,所以函数
有最小值,B正确;
又因为当 时,当 时, ,当 时, ,所以只需函数 的最小值小于0,函数 就有两个零点,D正确,
故选:BD.
11. 已知 为两个随机事件, 分别为其对立事件,则下列说法正确的是( )
A. 若 ,则
B. 若 ,则
C. 若 ,则
D. 若 ,则
【答案】BCD
【解析】
【分析】根据事件和概率加法公式,全概率,条件概率的概率公式以及独立事件与对立事件的概率公式,
对四个选项进行逐一的分析判断即可.
【详解】对于A, ,故A错误;
对于B,因为 ,所以 ,
所以 ,故B正确;
对于C,因为 ,
所以 ,所以 ,解得 ,故C正确;
对于D,因为 ,所以 ,又因为
,
所以 ,解得 ,故D正确.
故选:BCD.
第II卷(非选择题,共92分)
注意事项:
第II卷用黑色碳素笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.
三、填空题(本大题共3小题,每小题5分,共15分)
12. 某社团有3名女生、4名男生,随机选3名同学出来参加某个活动,用 表示选到男生的人数,则
的概率是__________.
【答案】
【解析】
【分析】根据题意,得到随机变量 的可能取值为 ,结合 ,即可求解.
【详解】由题意,某社团有3名女生、4名男生,随机选3名同学出来参加某个活动,
随机变量男生人数 的可能取值为 ,则 .
故答案为: .
13. 若 ,则 ______.(用数字作
答)【答案】
【解析】
【分析】利用赋值法,分别令 ,令 ,代入求解即可.
【详解】令 ,可得 ;
令 ,可得 ;
两式相减除以2,得 .
故答案为:
14. 已知定义在 上的函数 满足: ,则不等式
的解集为__________.
【答案】
【解析】
【分析】令 ,利用导数求得 为增函数,把不等式转化为 ,得到
,列出不等式组,即可求解.
【详解】令 ,则 ,所以 增函数,
是
不等式 可变形为 ,
因为 ,所以不等式 等价于 ,
所以 ,解得 ,所以不等式 的解集为 .故答案为: .
四、解答题(共77分.解答应写出文字说明,证明过程或演算步骤)
15. 在某次数学竞赛的初赛中,参赛选手需要从4道“圆锥曲线”和3道“函数与导数”共7道不同的试题中依
次抽取2道进行作答,抽出的题目不再放回.
(1)求选手甲第1次抽到“圆锥曲线”试题且第2次抽到“函数与导数”试题的概率;
(2)求选手甲第2次抽到“函数与导数”试题的概率;
(3)求选手甲第2次抽到“函数与导数”试题的条件下,第1次抽到“圆锥曲线”试题的概率.
【答案】(1)
(2)
(3)
【解析】
【分析】(1)法一:结合排列组合数运算利用古典概型概率公式求解即可;法二:利用条件概率公式求
解即可.
(2)利用全概率概率公式求解即可.
(3)利用条件概率公式求解即可.
【小问1详解】
记“选手甲第1次抽到“圆锥曲线”试题”为事件 ,“选手甲第2次抽到“函数与导数”试题”为事件 ,
法一: .
法二:由概率乘法公式可得 .
【小问2详解】
由全概率公式可得 .
【小问3详解】由条件概率公式可得 .
的
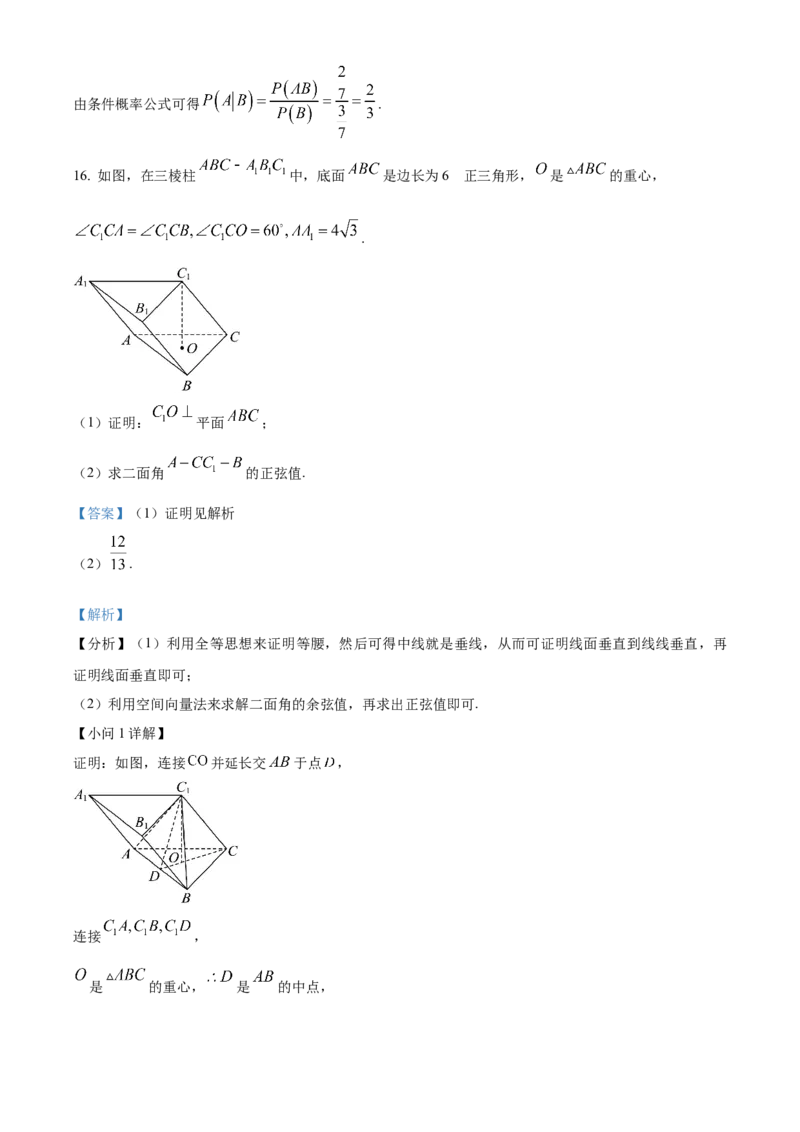
16. 如图,在三棱柱 中,底面 是边长为6 正三角形, 是 的重心,
.
(1)证明: 平面 ;
(2)求二面角 的正弦值.
【答案】(1)证明见解析
(2) .
【解析】
【分析】(1)利用全等思想来证明等腰,然后可得中线就是垂线,从而可证明线面垂直到线线垂直,再
证明线面垂直即可;
(2)利用空间向量法来求解二面角的余弦值,再求出正弦值即可.
【小问1详解】
证明:如图,连接 并延长交 于点 ,
连接 ,
是 的重心, 是 的中点,又底面 是正三角形, .
在 与 中, 为公共边,
, , ,
又 平面 平面 ,
平面 ,又 平面 , .
正 的边长为6, , ,
又 ,
在 中,由余弦定理可得, ,
, .
又 平面 平面 ,
平面 .
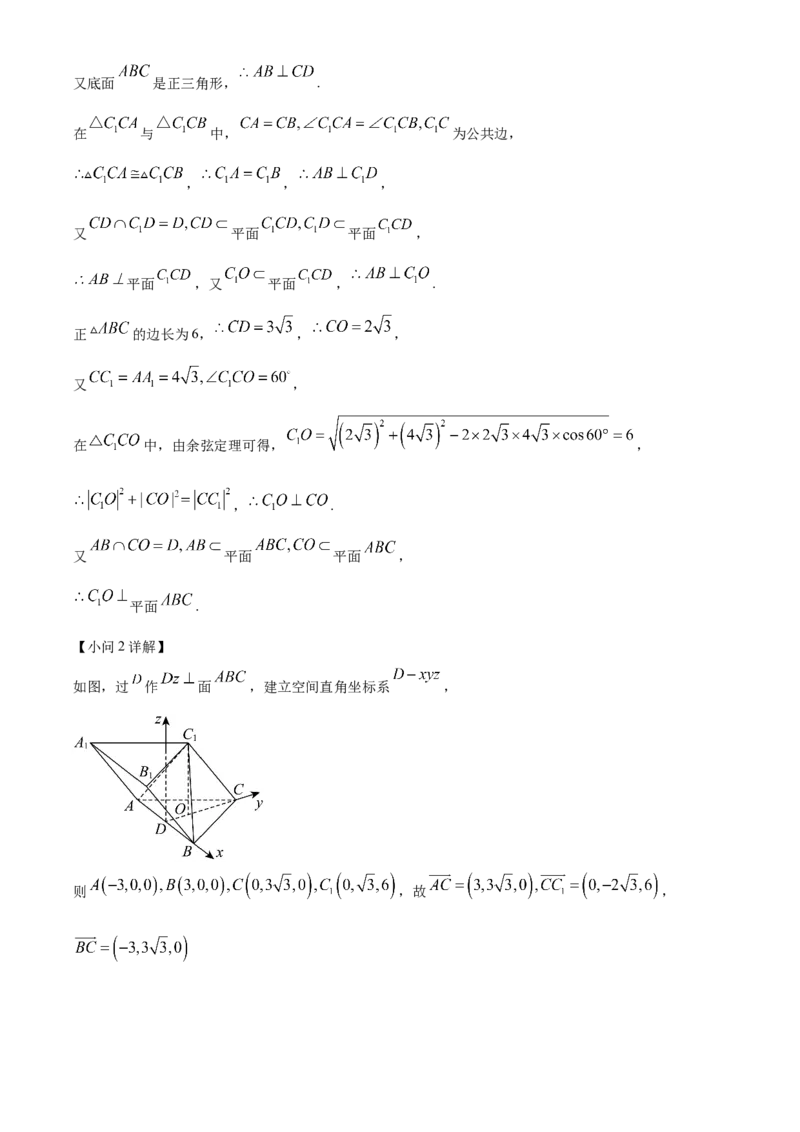
【小问2详解】
如图,过 作 面 ,建立空间直角坐标系 ,
则 ,故 ,设平面 的法向量 ,则 ,令 ,解得 ,则
.
设平面 的法向量 ,则 ,令 ,解得 ,则
.
设二面角 的大小为 ,则 ,
, ,即二面角 的正弦值为 .
17. 中国国际大数据产业博览会(简称“数博会”)从2015年在贵阳开办,至今已过9年.某校机器人社团为
了解贵阳市市民对历年“数博会”科技成果的关注情况,在贵阳市随机抽取了1000名市民进行问卷调查,问
卷调查的成绩 近似服从正态分布 ,且 .
(1)估计抽取市民中问卷成绩在80分以上的市民人数;
(2)若本次问卷调查得分超过80分,则认为该市民对“数博会”的关注度较高,现从贵阳市随机抽取3名
市民,记对“数博会”关注度较高的市民人数为随机变量 ,求 的分布列和数学期望.
【答案】(1)200人.
(2)分布列见解析,0.6
【解析】
【分析】(1)由变量 近似服从正态分布 ,求得 ,进而得到问卷成绩在80分
以上的市民人数;
(2)根据题意,得到随机变变量 ,结合对立重复试验的概率公式,求得相应的概率,列出
分布列,求得数学期望.
【小问1详解】
解:因为随机变量 近似服从正态分布 ,且 ,所以 ,所以 ,
所以估计抽取市民中问卷成绩在80分以上的市民人数为200人.
【小问2详解】
解:由题意,贵阳市市民对“数博会”关注度较高的概率为 ,且 ,
所以随机变量 的分布列为 ,
所以随机变量 的分布列为:
0 1 2 3
.
0.512 0.384 0096 0.008
所以随机变量 的均值为 .
18. 已知圆: 的圆心为椭圆 的右焦点 ,且椭圆 的离心
率为 .
(1)求椭圆 的标准方程;
(2)过点 且不与 轴重合的直线 交椭圆 于 两点, 为 的中点, 为坐标原点,分别过
作椭圆 的切线,两切线相交于点 .
(i)求证: 三点共线;
(ii)当 不与 轴垂直时,求 的最小值.
【答案】(1)
(2)(i)证明见解析;(ii) .
【解析】【分析】(1)根据焦点坐标和离心率求得 , ,即可求解椭圆方程;
(2)(i)分 斜率不存在和存在两种情况讨论,当 斜率存在时,设出方程与椭圆方程联立,韦达定理求
出 的坐标,利用判别式法求出切线方程,进而求得 的坐标为 ,即可证明
三点共线;
(ii)利用距离公式和弦长公式分别求出 ,即可求解.
【小问1详解】
由圆: 即 可得:圆心 ,所以 ,
又离心率 ,所以 ,所以 ,
所以椭圆标准方程为 .
【小问2详解】
(i)①当 斜率不存在时, 轴,
由椭圆的对称性可知, 均在 轴上,所以 三点共线.
②当 斜率存在时,设 的方程为 ,且 ,
联立方程组 可得: ,
则 ,点 的坐标为 ,
所以 所在的直线的方程为 ,
先证:椭圆 上一点 处的切线方程为 ,当切线斜率存在时,设过点 的切线方程为 ,
联立方程 ,整理得 ,
由 可得 ,所以
由韦达定理可知 ,即 ,
把 代入 中,得 ,
所以 ,化简得 .
当切线斜率不存在时,过 的切线方程为 ,满足上式.
综上,椭圆上一点 的切线方程为 .
所以椭圆 在 处的切线方程为 ,
联立方程组 解得点 的坐标为 ,
,故 三点共线.
(ii)由(i)可知, ,
又 三点共线,所以 ,所以 ,即点 化简得 ,
所以 , ,
所以
,当且仅当 ,即 时,等号成立.
所以 的最小值为 .
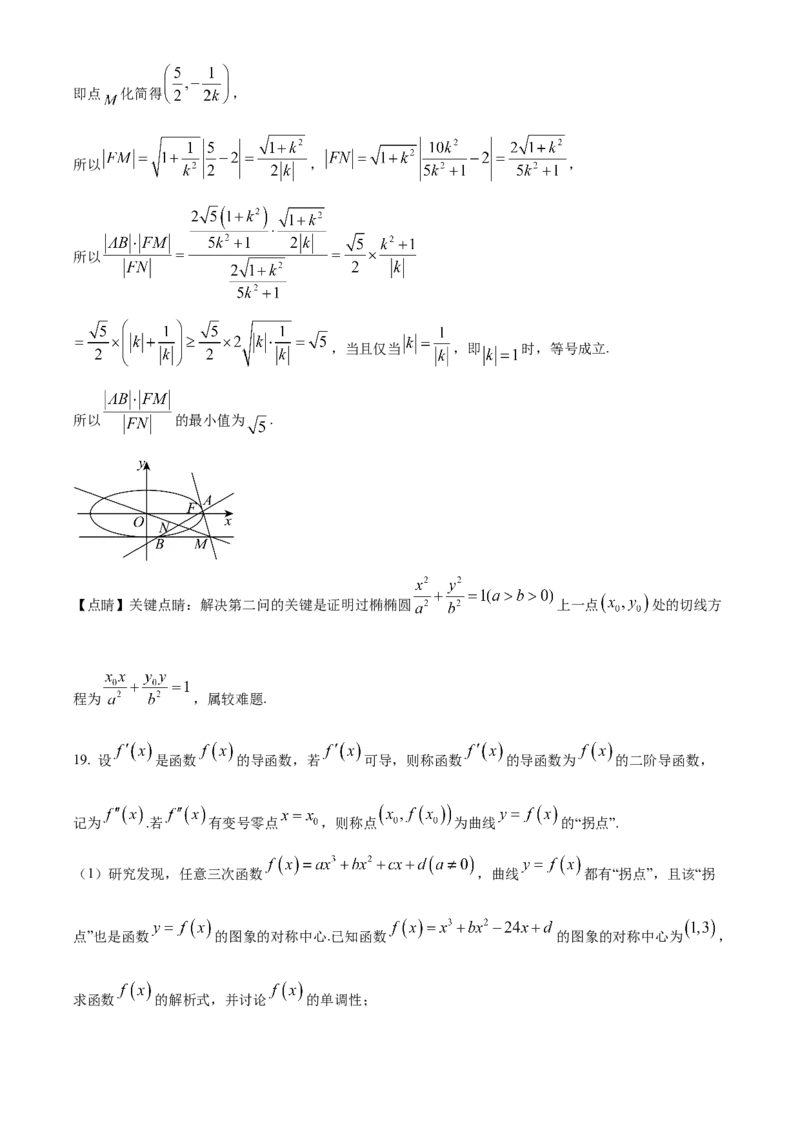
【点睛】关键点睛:解决第二问的关键是证明过椭椭圆 上一点 处的切线方
程为 ,属较难题.
19. 设 是函数 的导函数,若 可导,则称函数 的导函数为 的二阶导函数,
记为 .若 有变号零点 ,则称点 为曲线 的“拐点”.
(1)研究发现,任意三次函数 ,曲线 都有“拐点”,且该“拐
点”也是函数 的图象的对称中心.已知函数 的图象的对称中心为 ,
求函数 的解析式,并讨论 的单调性;(2)已知函数 .
(i)求曲线 的“拐点”;
.
(ii)若 ,求证:
【答案】(1) ,函数 在 上单调递增,在 上单调递减,
在 上单调递增.
(2)(i) ;(ii)证明见解析
【解析】
【分析】(1)根据“拐点”的定义,对函数 求导列式求解 ,利用导数研究函数
的单调性即可求解,
(2)(ⅰ)根据“拐点”的定义,对函数 求导,利用二阶导函数的异号零点得出结果;
(ⅱ)由(i)可得函数 在 上单调递增,将要证的不等式转化为 ,构造函
数 ,利用导数研究函数的单调性,再根据函数 的单调性得到关于 的
不等式,即可证明.
【小问1详解】
, , ,
又函数 的图象的对称中心为 ,即拐点为 ,
解得 ,, ,
函数 在 上为正,在 上为负,在 上为正,
函数 在 上单调递增,在 上单调递减,在 上单调递增.
【小问2详解】
(i) ,
, .
显然, 在 上单调递增,且 ,
是 的变号零点,
又 ,
曲线 的拐点是 .
(ii)由(i)可得,当 时, 单调递减;
当 时, 单调递增;
,
函数 在 上单调递增,不妨设 .
要证 ,即证 ,即证 ,.
又 ,即证 ,即证
令 ,则 ,
,
函数 在 上单调递增,又 ,
函数 在 上单调递减,在 上单调递增.
得证,即 成立.
【点睛】方法点睛:处理此类双变量问题有两个策略:
一是转化,即从已知条件入手,寻找双变量所满足的不等式,并把含双变量的不等式转化为含单变量的不
等式;
二是巧妙构造函数,再借用导数判断函数的单调性,从而求解.