文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(13)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知复数 满足 ,则复数 在复平面内对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
【解析】由题意设 ,所以 ,
所以 ,解得 ,所以 对应点 位于第四象限.
故选:D.
2.已知 成等比数列,且2和8为其中的两项,则 的最小值为( )
A. B. C. D.
【答案】B
【解析】由题意,要使 最小,则 都是负数,
则 和 选择2和8,设等比数列的公比为 ,
当 时, ,所以 ,所以 ;
当 时, ,所以 ,所以 ;
综上, 的最小值为 .
故选:B.
3.已知直线 和直线 ,则“ ”是“ ”的
( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
【答案】A
【解析】若直线 和直线 平行,
则 ,解得 ,
所以“ ”是“ ”的充要条件,
故选:A
4.设集合 , ,则( )
A. B. C. D.
【答案】D
【解析】 ,即 ,则 ,解得 ,更多全科试卷,请关注公众号:高中试卷君
所以 , ,
所以 ,从而 .
故选:D.
5.将12名志愿者(含甲、乙、丙)安排到三个地区做环保宣传工作,每个地区至少需要安排 3人,则
甲、乙、丙3人恰好被安排到同一个地区的安排方法总数为( )
A. 3129 B. 4284 C. 18774 D. 25704
【答案】C
【解析】先分类讨论人员分组情况.
当甲、乙、丙所在组恰有3人时,余下9人分成2组,有 种方法;
当甲、乙、丙所在组恰有 4 人时,先从其他 9 人中选 1 人到这组,再将余下 8 人分成 2 组,有
种方法;
当甲、乙、丙所在组恰有5人时,先从其他9人中选2人到这组,余下7人分成2组,
有 种方法
当甲、乙、丙所在组恰有6人时,先从其他9人中选3人到这组,余下6人分成2组,
有 种方法.
再将三组人员分配到三个地区.
因为这三组分配到三个地区有 种方法,
所以安排方法总数为 .
故选:C.
6.设A,B为两个事件,已知 ,则 ( )
A. B. C. D.
【答案】B
【解析】由 ,得 ,显然 ,
因此 ,所以 .
故选:B
7.如图,已知正方形 的边长为4,若动点 在以 为直径的半圆上(正方形 内部,含
边界),则 的取值范围为( )
A. B. C. D.
【答案】B更多全科试卷,请关注公众号:高中试卷君
【解析】取 的中点 ,连接 ,如图所示,
所以 的取值范围是 ,即 ,
又由 ,
所以 .
故选:B.
8.已知 分别为双曲线 的左、右焦点,过 向双曲线的一条渐近线引
垂线,垂足为点 ,且 ( 为坐标原点),则双曲线 的渐近线方程为(
)
A. B.
C. D.
【答案】D
【解析】设双曲线 焦距为 ,则 、 ,
不妨设渐近线 的方程为 ,如图:
因为直线 与直线 垂直,则直线 的方程为 ,
联立 可得 ,即点 ,
所以, ,更多全科试卷,请关注公众号:高中试卷君
因 为,所以 ,
又 ,故 ,
所以,
,
整理可得 ,
所以 ,又 ,
所以 ,
故该双曲线C的渐近线方程为 .
故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知直线l,m,平面 , ,则下列说法错误的是( )
A. , ,则
B. , , , ,则
C. , , ,则
D. , , , , ,则
【答案】ABC
【解析】选项A中,m可能在 内,也可能与 平行,故A错误;
选项B中, 与 也可能相交,故B错误;
选项C中, 与 也可能相交,故C错误;
选项D中,依据面面平行 判的定定理可知 ,故D正确.
故选:ABC.
10.如图,已知抛物线 的焦点为 ,抛物线 的准线与 轴交于点 ,过
点 的直线 (直线 的倾斜角为锐角)与抛物线 相交于 两点(A在 轴的上方, 在
轴的下方),过点 A作抛物线 的准线的垂线,垂足为 ,直线 与抛物线 的准线相交于点
,则( )更多全科试卷,请关注公众号:高中试卷君
A. 当直线 的斜率为1时, B. 若 ,则直线 的斜率为2
C. 存在直线 使得 D. 若 ,则直线 的倾斜角为
【答案】AD
【解析】易知 ,可设 ,设 ,
与抛物线方程联立得 ,
则 ,
对于A项,当直线 的斜率为1时,此时 ,
由抛物线定义可知 ,故A正确;
易知 是直角三角形,若 ,
则 ,
又 ,所以 为等边三角形,即 ,此时 ,故B错误;
由上可知
,
即 ,故C错误;
若 ,
又知 ,所以 ,
则 ,即直线 的倾斜角为 ,故D正确.
故选:AD更多全科试卷,请关注公众号:高中试卷君
11.已知定义在 上的函数 满足 ,且 是奇函数.则
( )
A. B.
C. 是 与 的等差中项 D.
【答案】ACD
【解析】因为 ,
所以 ,
两式相减得 ,
所以 的周期为4.
因为 是奇函数,
所以 ,所以 ,
即 ,
令 ,得 .
因为 ,
令 ,得 ,
所以 ,即 .
因为 ,
令 ,得 ,
所以 ,
所以 ,
所以 ,故A正确.
因为 ,
所以 ,即 ,所以 .
因为 , ,所以B错误.
因为 , ,
所以 ,
所以 是 与 的等差中项,故C正确.
因为 ,
所以 ,故D正确.
故选:ACD
三、填空题:本题共3小题,每小题5分,共15分.
12.样本数据16,24,14,10,20,30,12,14,40的中位数为________
【答案】16
【解析】将这些数据从小到大排列可得:10,12,14,14,16,20,24,30,40,
则其中位数为16.
故答案为:16
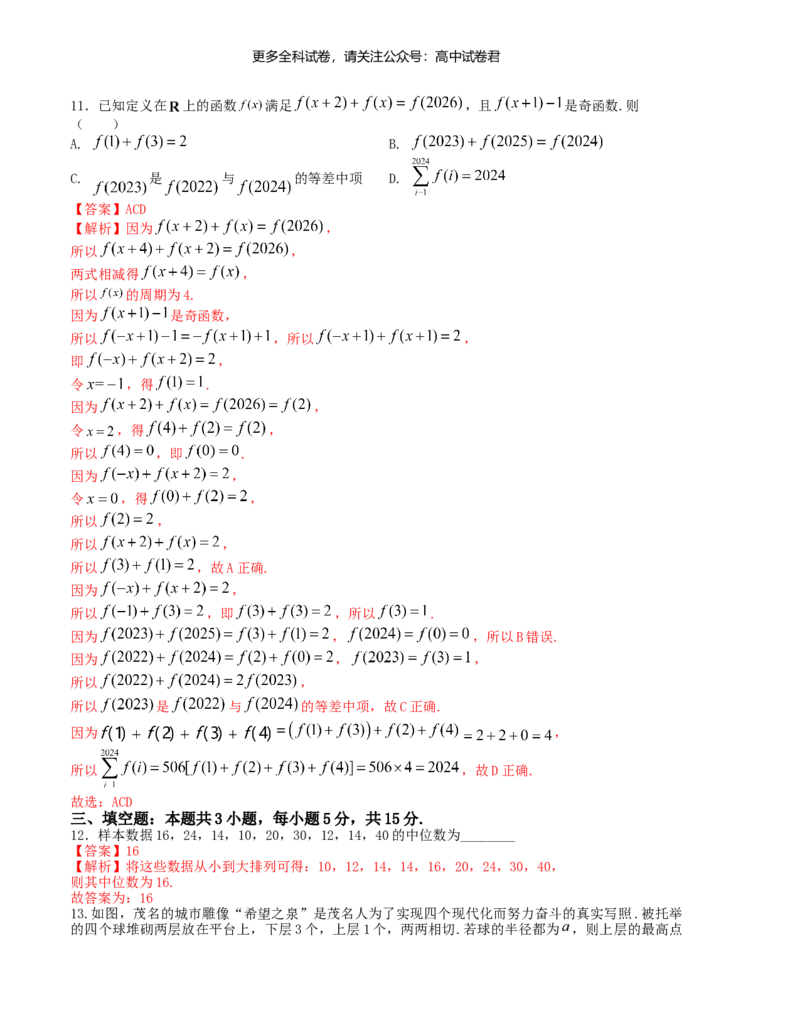
13.如图,茂名的城市雕像“希望之泉”是茂名人为了实现四个现代化而努力奋斗的真实写照.被托举
的四个球堆砌两层放在平台上,下层3个,上层1个,两两相切.若球的半径都为 ,则上层的最高点更多全科试卷,请关注公众号:高中试卷君
离平台的距离为______.
【答案】
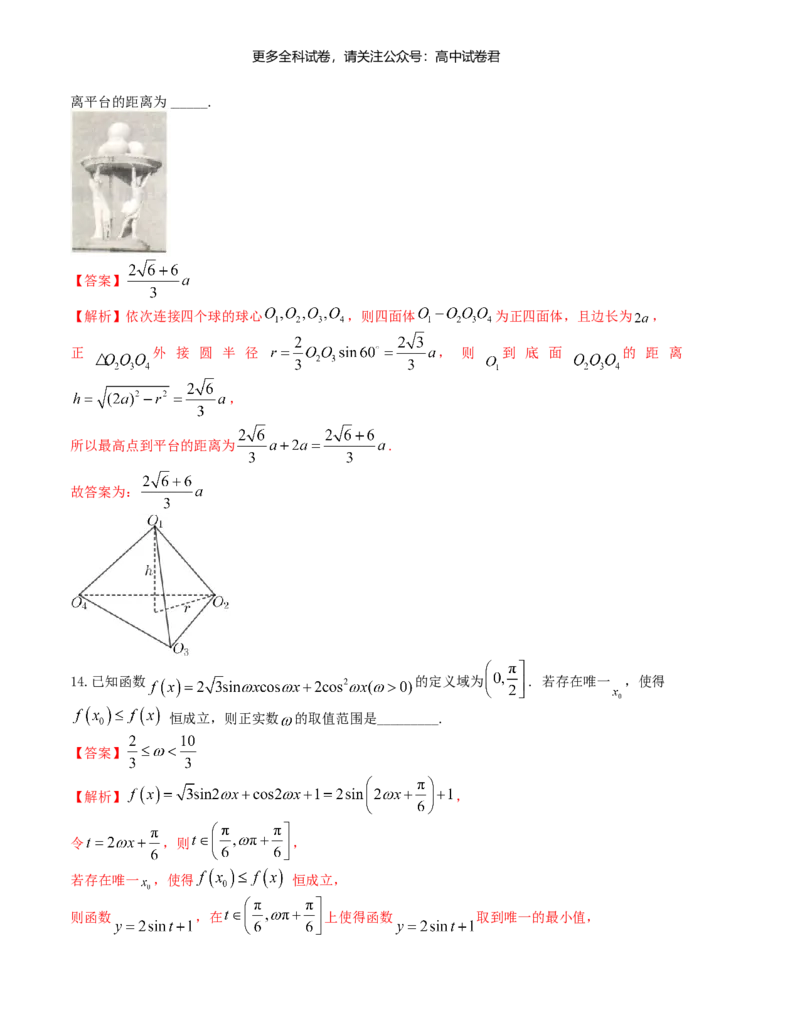
【解析】依次连接四个球的球心 ,则四面体 为正四面体,且边长为 ,
正 外 接 圆 半 径 , 则 到 底 面 的 距 离
,
所以最高点到平台的距离为 .
故答案为:
14.已知函数 的定义域为 . 若存在唯一 ,使得
恒成立,则正实数 的取值范围是_________.
【答案】
【解析】 ,
令 ,则 ,
若存在唯一 ,使得 恒成立,
则函数 ,在 上使得函数 取到唯一的最小值,更多全科试卷,请关注公众号:高中试卷君
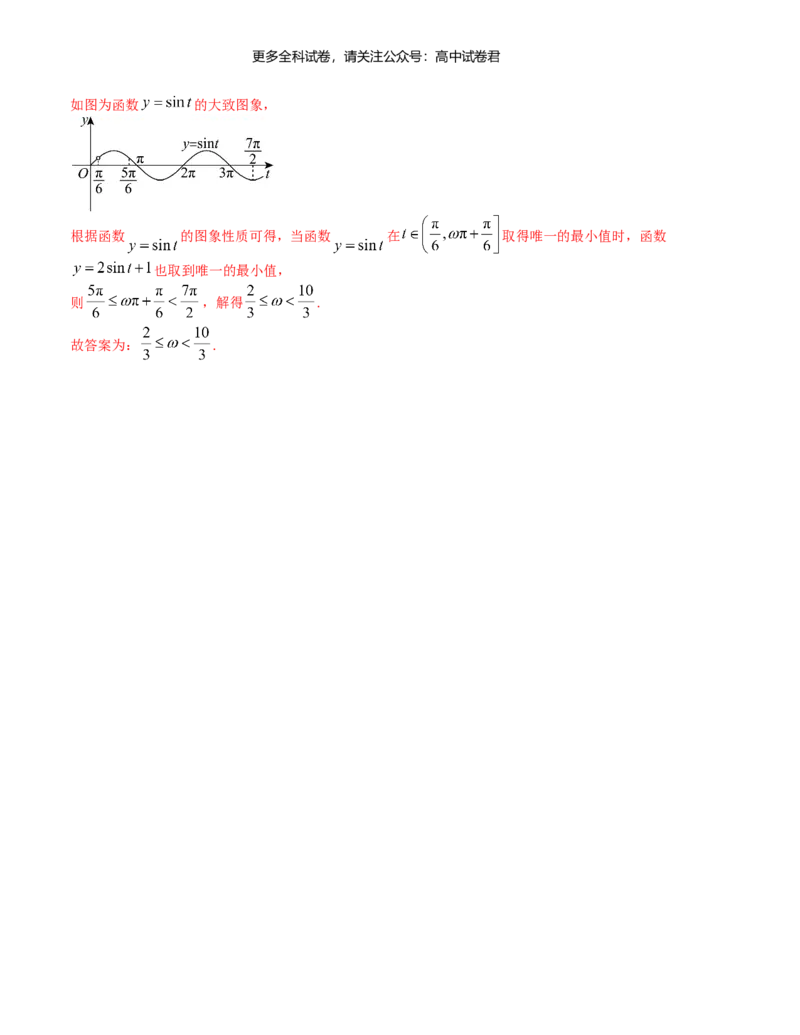
如图为函数 的大致图象,
根据函数 的图象性质可得,当函数 在 取得唯一的最小值时,函数
也取到唯一的最小值,
则 ,解得 .
故答案为: .