文档内容
5.2.2 同角三角函数的基本关系
(用时45分钟)
【选题明细表】
知识点、方法 题号
应用同角三角函数关系求值 1,2,4,6
三角函数式的化简、求值 7,8,9,10
证明三角函数式 12
“sin α±cos α”同“sin αcos α”间的关系 5,3,11,13
基础巩固
1.若α是第四象限角,tan α=-,则sin α=( )
A. B.-
C. D.-
【答案】D
【解析】因为tan α==-,sin2α+cos2α=1,
所以sin α=±.因为α是第四象限角,所以sin α=-.
2.下列结论中成立的是( )
A.sin α= 且cos α=
B.tan α=2且 =
C.tan α=1且cos α=±
D.sin α=1且tan α·cos α=1
【答案】C
【解析】由平方关系知sin2α+cos2α=1,故A错.由tan α=2得 =2,故 = ,因此B错.因为tan
α=1,
故α终边在第一或三象限,因此cos α=± 正确.当sin α=1时,α= +2kπ(k∈Z),此时tan α无意义,故D错.
3.已知2cos α+sin α= ,α是第四象限角,则tan α= ( )
A. B.- C. 3 D.-3
【答案】B
【解析】因为α是第四象限角,所以cos α>0,sin α<0,设x=cos α> 0,y=sin α<0,
则 解方程组得
所以tan α= =- .
4.已知sin α= ,则sin4α-cos4α的值为( )
A.- B. - C. D.
【答案】B
【解析】sin4α-cos4α=(sin2α+cos2α)·(sin2α-cos2α)=sin2α-cos2α =2sin2α-1=2× -1=- .
5.设A是△ABC的一个内角,且sin A+cos A= ,则这个三角形是 ( )
A.锐角三角形 B.钝角三角形
C.等边三角形 D.直角三角形
【答案】B
【解析】将sin A+cos A= 两边平方得sin2A+2sin Acos A+cos2A= ,又sin2A+cos2A=1,故sin Acos A=-
.因为00,则cos A<0,即A是钝角.
6.在△ABC中,若tan A= ,则sin A=________,cos A=________.【答案】
【解析】由tan A= >0且角A是△ABC的内角可得00,cos α<0.
故tan α=tan α
=tan α=·
=·=-1.
能力提升
9.已知sin α+2cos α=0,则2sin αcos α-cos2α的值是________.
【答案】-1.
【解析】由sin α=-2cos α,所以tan α=-2,
则2sin αcos α-cos2α= = = =-1.
10.已知α是第二象限角,则 + =________.【答案】-1.
【解析】因为α是第二象限角,
所以sin α>0,cos α<0,
所以 + = + =-1.
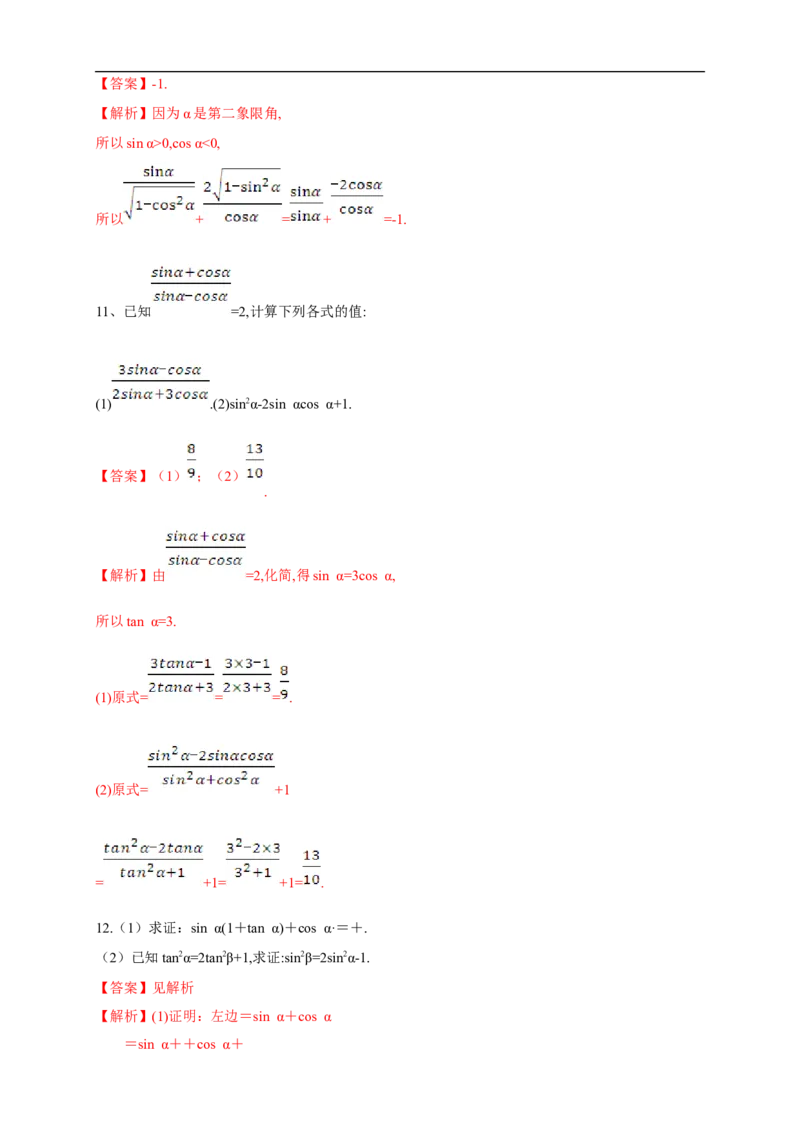
11、已知 =2,计算下列各式的值:
(1) .(2)sin2α-2sin αcos α+1.
【答案】(1) ;(2)
.
【解析】由 =2,化简,得sin α=3cos α,
所以tan α=3.
(1)原式= = = .
(2)原式= +1
= +1= +1= .
12.(1)求证:sin α(1+tan α)+cos α·=+.
(2)已知tan2α=2tan2β+1,求证:sin2β=2sin2α-1.
【答案】见解析
【解析】(1)证明:左边=sin α+cos α
=sin α++cos α+=+
=+=右边.
即原等式成立.
(2)证明:因为tan2α=2tan2β+1,
所以tan2α+1=2tan2β+2,
所以 +1=2 ,通分可得 = ,
即cos2β=2cos2α,所以1-sin2β=2(1-sin2α),
即sin2β=2sin2α-1.
素养达成
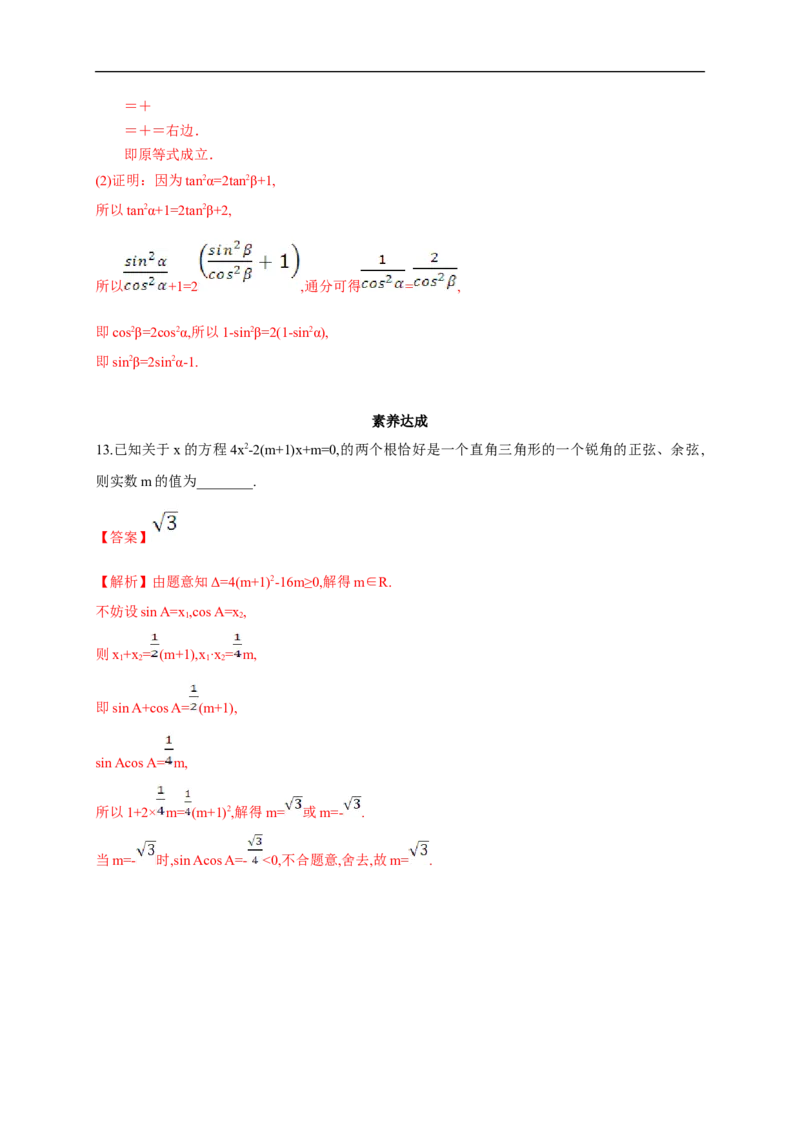
13.已知关于x的方程4x2-2(m+1)x+m=0,的两个根恰好是一个直角三角形的一个锐角的正弦、余弦,
则实数m的值为________.
【答案】
【解析】由题意知Δ=4(m+1)2-16m≥0,解得m∈R.
不妨设sin A=x ,cos A=x ,
1 2
则x+x= (m+1),x ·x= m,
1 2 1 2
即sin A+cos A= (m+1),
sin Acos A= m,
所以1+2× m= (m+1)2,解得m= 或m=- .
当m=- 时,sin Acos A=- <0,不合题意,舍去,故m= .