文档内容
5.3.1函数的单调性(1) -A基础练
一、 选择题
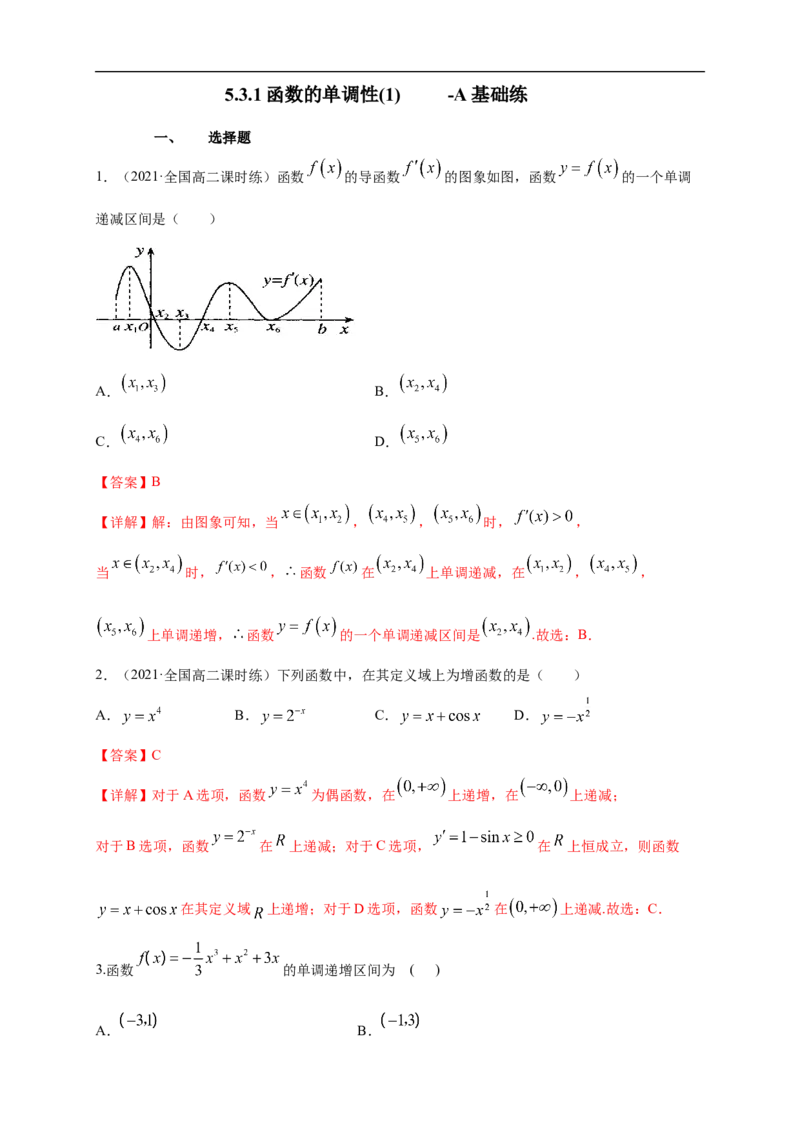
1.(2021·全国高二课时练)函数 的导函数 的图象如图,函数 的一个单调
递减区间是( )
A. B.
C. D.
【答案】B
【详解】解:由图象可知,当 , , 时, ,
当 时, , 函数 在 上单调递减,在 , ,
上单调递增, 函数 的一个单调递减区间是 .故选:B.
2.(2021·全国高二课时练)下列函数中,在其定义域上为增函数的是( )
A. B. C. D.
【答案】C
【详解】对于A选项,函数 为偶函数,在 上递增,在 上递减;
对于B选项,函数 在 上递减;对于C选项, 在 上恒成立,则函数
在其定义域 上递增;对于D选项,函数 在 上递减.故选:C.
3.函数 的单调递增区间为 ( )
A. B.C. 和 D. 和
【答案】B
【 解 析 】 由 , 得 , 令 , 即 , 得
,解得 ,即 的单调递增区间为 .故选B.
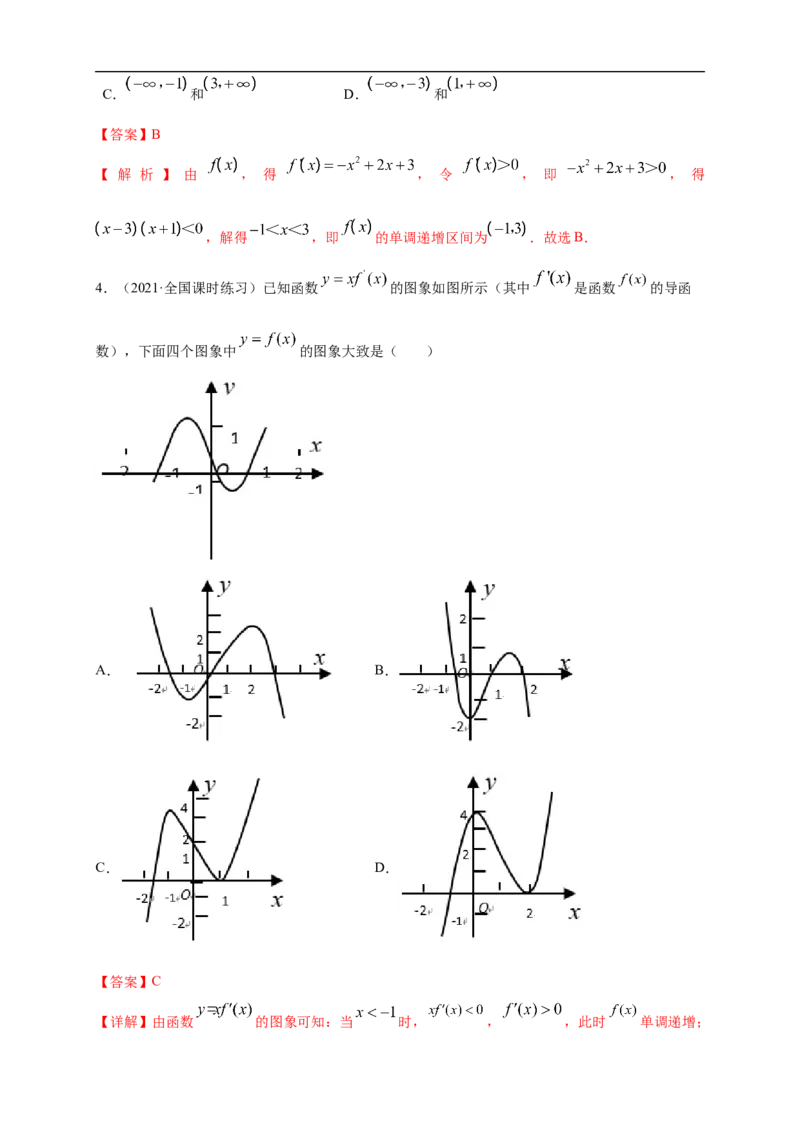
4.(2021·全国课时练习)已知函数 的图象如图所示(其中 是函数 的导函
数),下面四个图象中 的图象大致是( )
A. B.
C. D.
【答案】C
【详解】由函数 的图象可知:当 时, , ,此时 单调递增;当 时, , ,此时 单调递减;
当 时, , ,此时 单调递减;
当 时, , ,此时 单调递增.故选:C
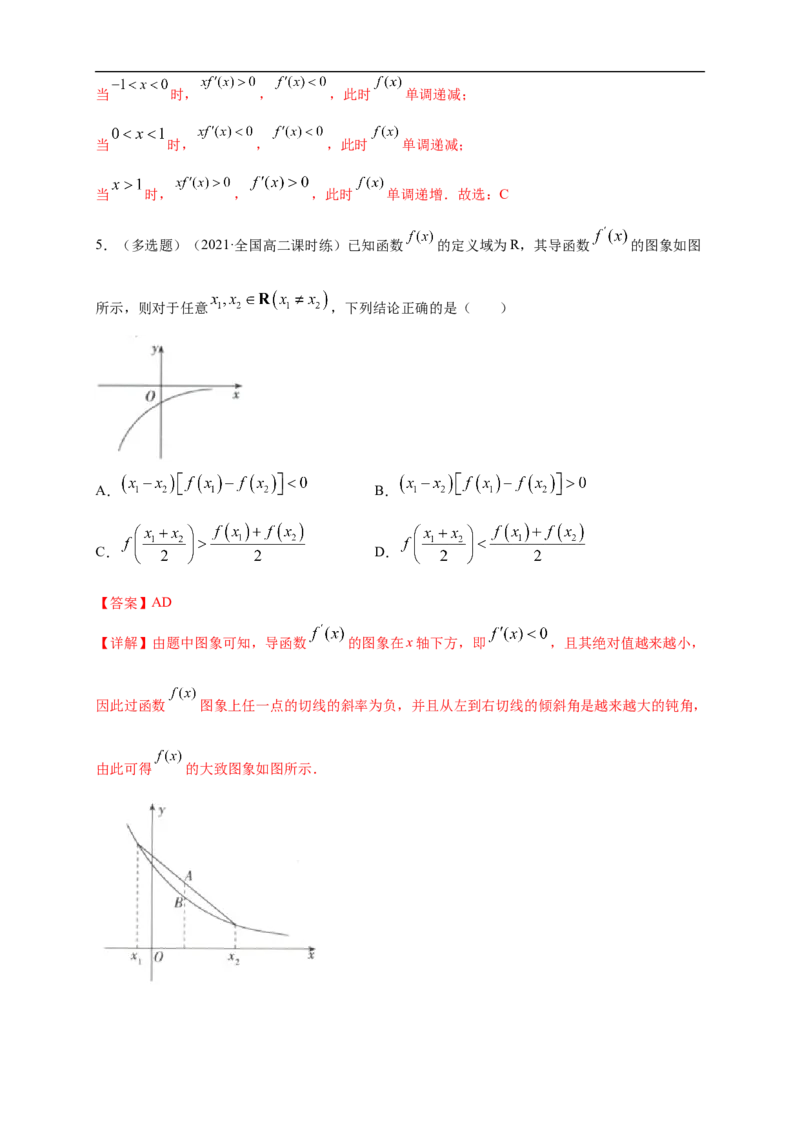
5.(多选题)(2021·全国高二课时练)已知函数 的定义域为R,其导函数 的图象如图
所示,则对于任意 ,下列结论正确的是( )
A. B.
C. D.
【答案】AD
【详解】由题中图象可知,导函数 的图象在x轴下方,即 ,且其绝对值越来越小,
因此过函数 图象上任一点的切线的斜率为负,并且从左到右切线的倾斜角是越来越大的钝角,
由此可得 的大致图象如图所示.A选项表示 与 异号,即 图象的割线斜率 为负,故A正
确;B选项表示 与 同号,即 图象的割线斜率 为正,故B
不正确; 表示 对应的函数值,即图中点B的纵坐标, 表示当
和 时所对应的函数值的平均值,即图中点A的纵坐标,显然有
,故C不正确,D正确.故选:AD.
6.(多选题)(2021·湖北高二期末)已知函数 , ,则下列说法正确的有(
)
A. 是奇函数
B. 是周期函数
C.曲线 在点 处的切线方程为
D.在区间 上, 单调递增
【答案】AC
【详解】解:对A, 的定义域为 关于原点对称,
,故 是奇函数,即A正确;
对B,若 是周期函数,则存在非零常数 ,使 ,
,易知:不存在非零常数 ,使 ,故 不是周期函数;故B错误;
对C, , ,
又 ,故 在点 处的切线方程为:
,
即 ,故C正确;对D, ,当 ,
故 ,故在 上, 单调递减.故选:AC.
二、 填空题
7.(2020·山东泰安一中高二期中)函数 的单调增区间为___________
【答案】
【详解】 , ,∴ 在 上恒成立,所以函数的单调增区间为
8.(2020·海林市朝鲜族中学高二课时练)函数y=x2-4ln x 的单调递减区间是________.
【答案】(0, )
【详解】∵y′=2x﹣ ,令y′<0,解得:0<x< .
9.(2021·全国高二课时练)已知 满足 为其导函数,且导函数
的图象如图所示,则 的解集是_________.【答案】
【详解】解:由 的导函数 的图象知: 在 上单调递减,在 上单调递
增,
当 时,由 ,得 ,
当 时,由 ,得 ,
综上所述: 的解集为 .故答案为: .
10.(2020·上海高二课时练习)若函数 在区间 上是增函数,则实数a
的取值范围是__________.
【答案】
【详解】 函数 的对称轴为 ,且函数开口向上,
,故答案为: .
三、解答题
11.(2021·全国高二课时练)求下列函数的单调区间.
(1) ;
(2) ;
(3) .
【详解】(1)易知函数的定义域为 .,令 ,解得 (舍去),用 分割定义域,得下表:
x
- +
∴函数 的单调递减区间为 ,单调递增区间为 .
(2)易知函数的定义域为 .
,令 ,得 或 ,
当x变化时, 的变化情况如下表:
x
- + -
∴ 的单调递减区间为 和 ,单调递增区间为 .
(3)易知函数的定义域为 .
,令 ,得 或 ,当x变化时, 的变化情况如下表:
x
+ - - +
∴函数 的单调递减区间为 和 ,单调递增区间为 和 .
12.(2020·福建三明一中高二月考)已知函数 .(1)若 在区间 上为增函数,求a的取值范围.
(2)若 的单调递减区间为 ,求a的值.
【详解】(1)因为 ,且 在区间 上为增函数,
所以 在 上恒成立,即 在(1,+∞)上恒成立,
所以 在 上恒成立,所以 ,即a的取值范围是
(2)由题意知 .因为 ,所以 .
由 ,得 ,
所以 的单调递减区间为 ,
又已知 的单调递减区间为 ,
所以 ,
所以 ,即 .