文档内容
5.3.1 函数的单调性
【题组一 求函数的单调区间】
1
1.(2020·河南信阳·高二期末(文))已知函数f(x)= x2-lnx,则其单调增区间是( )
2
A.¿ B.[0,1] C.(0,+∞) D.(1,+∞)
【答案】D
1
【解析】f(x)= x2-lnx,定义域为(0,+∞)
2
1
令f'(x)=x- >0解得x>1
x
1
故函数f(x)= x2-lnx单调增区间是(1,+∞)故选D
2
2.(2020·吉林净月高新技术产业开发区·东北师大附中高二月考(理))函数 的单调递
增区间是( )
A. B. C. D.
【答案】D
【解析】函数 的定义域为 , ,令 ,解得 .
因此,函数 的单调递增区间是 .故选:D.
3.(2020·北京丰台·高三二模)已知函数 ,则
A.是奇函数,且在定义域上是增函数
B.是奇函数,且在定义域上是减函数
C.是偶函数,且在区间 上是增函数
D.是偶函数,且在区间 上是减函数
【答案】B
【解析】根据题意,函数 ,则有 ,解可得 ,即 的定义域为 ;设任意 , ,则函数 为奇函数;
,其导数 ,
在区间 上, ,则 为 上的减函数;故选: .
4.(2020·山西省古县第一中学高二期中(理))函数 的单调递增区间是( )
A. B. C.(1,4) D.(0,3)
【答案】B
【解析】 , ,解不等式 ,解得 ,
因此,函数 的单调递增区间是 ,故选B.
5.(2020·沙坪坝·重庆一中高三月考)函数 的一个单调减区间是( )
A. B. C. D.
【答案】A
【解析】 ,该函数的定义域为 ,
,
,可得 ,
令 ,可得 ,即 ,解得 .
所以,函数 的单调递减区间为 .当 时,函数 的一个单调递减区间为 ,
,
对任意的 , , ,
,
故函数 的一个单调递减区间为 .
故选:A.
6.(2020·安徽高三开学考试(理))若曲线 在点 处的切线过点 ,则函数
的单调递减区间为( )
A. B.
C. D. ,
【答案】D
【解析】由题意 ,
∴ ,又 ,
故曲线在点 处的切线方程为 ,
将点 代入可得 ,则 ,
令 ,
所以 或 ,
故函数在 , 上单调递减.
故选:D
7.(2020·云南昆明一中高三其他(理))函数 的单调递减区间是( )
A. B. C. D.
【答案】D
【解析】函数的定义域是 , ,
令 ,解得 ,
故函数 在 上单调递减,选:D.
【题组二 已知单调性求参数】
1.(2020·四川省绵阳江油中学高二期中(文))已知 在 上为单
调递增函数,则 的取值范围为( )
A. B. C. D.
【答案】D
【解析】 ,
因为 在 上为单调递增,等价于 恒成立.即 在 上恒成立.因为 ,当 时,取“ ”,
所以 ,即 的范围为 .故选:D
2.(2020·河南南阳·高二期末(理))函数 在区间 上单调递减,则实数 的取
值范围是( )
A. B. C. D.
【答案】B
【解析】 , ,
由题意可知,不等式 对于任意的 恒成立,
所以, ,解得 .
因此,实数 的取值范围是 .
故选:B.
3.(2020·佳木斯市第二中学高二期末(文))“a≤-1”是“函数f(x)=ln x-ax在[1,+∞)上为单调函数”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】因为函数f(x)=ln x-ax在[1,+∞)上为单调函数,
所以 在[1,+∞)上恒成立或 在[1,+∞)上恒成立,
即 或 ,
从而 或因为“ ”是“ 或 ” 充分不必要条件,
所以“a≤-1”是“函数f(x)=ln x-ax在[1,+∞)上为单调函数”的充分不必要条件,
故选:A
4.(2020·赣州市赣县第三中学高二月考(文))已知函数 ,若函数 在
上为增函数,则正实数 的取值范围为( )
A. B. C. D.
【答案】D
【解析】函数 , ,
因为函数 在 上为增函数,所以 在 上恒成立,
又 ,所以 在 上恒成立,即 在 上恒成立,
令 ,所以 ,故选:D
5.(2019·四川树德中学高二月考(理)) 在 单调递增,则 的范
围是__________.
【答案】
【解析】 ,则 ,
因为函数 在 上单调增,可得 在 上恒成立,
即 ,令 ,则 , ,所以 ,因为 在 上是增函数,
所以其最大值为 ,
所以实数 的取值范围是 .
6.(2020·黑龙江让胡路·铁人中学高二期末(理))设函数 在 , 上单调递增,则
的取值范围是( )
A. , B. , C. D.
【答案】B 在 , 上单调递增,
在 , 上恒成立,即 ,
而函数 在 , 上单调递增, 当 时, , ,
的取值范围是 , .故选: .
7.(2020·西夏·宁夏大学附属中学高二期中(理))若函数 在区间 上单调递减,
则实数t的取值范围是( )
A. B. C. D.
【答案】A
【解析】因为函数 在区间 上单调递减,
所以 在 恒成立,
所以 即 解得: .8.(2020·临猗县临晋中学高二期末(理))设函数 在区间 上单调递减,
则实数 的取值范围是( )
A. B. C. D.
【答案】A
【解析】依题意 ,由此排除CD选项.
由 ,解得 ,
所以函数 的单调递减区间为 .
由此排除B选项,只有A选项正确.
证明如下:
由于 在区间 上单调递减,
所以 ,解得 .
故选:A
【题组三 单调性与图像】
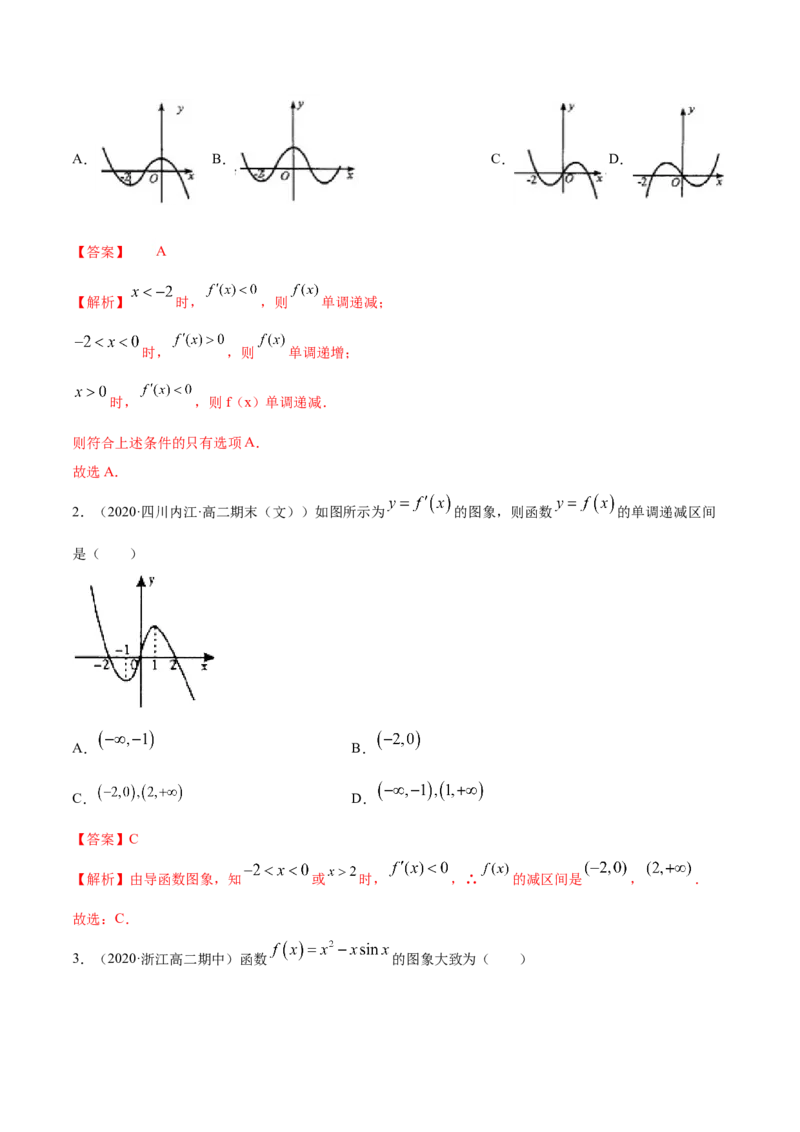
1.(2020·陕西省商丹高新学校高二月考(理))已知函数 的导函数 的图象如图所示,那么函
数 的图象最有可能的是( )A. B. C. D.
【答案】 A
【解析】 时, ,则 单调递减;
时, ,则 单调递增;
时, ,则f(x)单调递减.
则符合上述条件的只有选项A.
故选A.
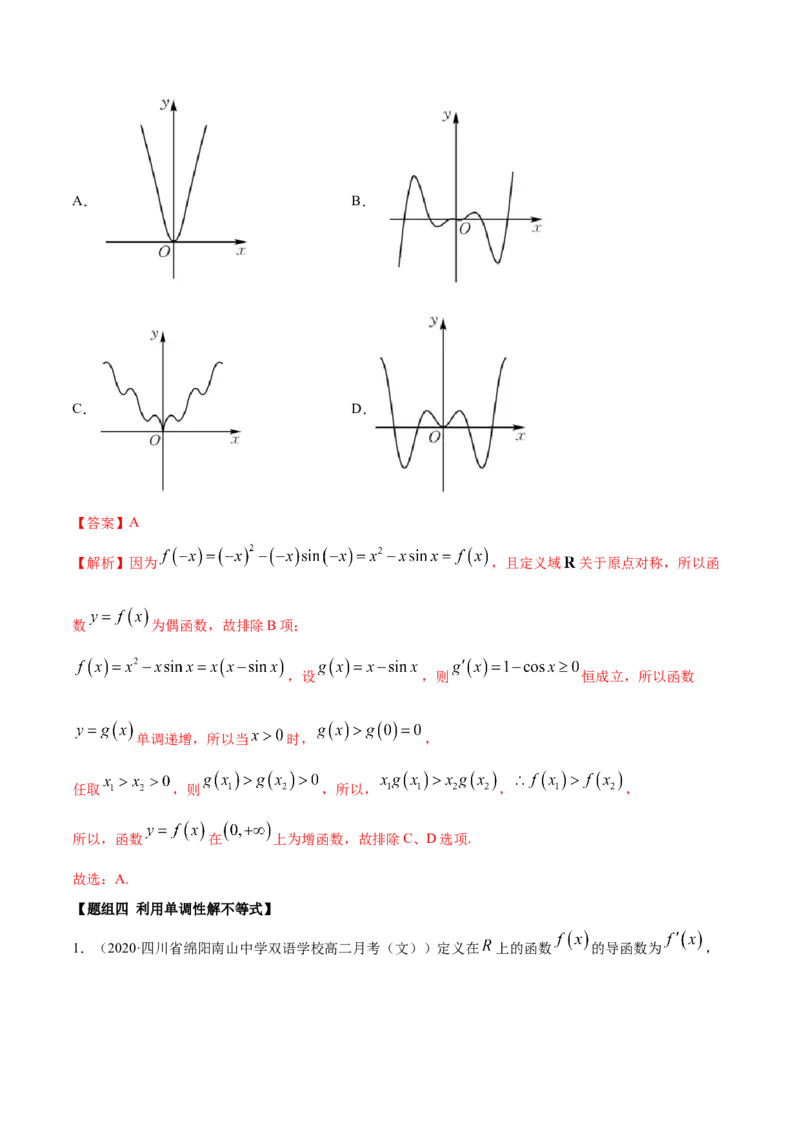
2.(2020·四川内江·高二期末(文))如图所示为 的图象,则函数 的单调递减区间
是( )
A. B.
C. D.
【答案】C
【解析】由导函数图象,知 或 时, ,∴ 的减区间是 , .
故选:C.
3.(2020·浙江高二期中)函数 的图象大致为( )A. B.
C. D.
【答案】A
【解析】因为 ,且定义域 关于原点对称,所以函
数 为偶函数,故排除B项;
,设 ,则 恒成立,所以函数
单调递增,所以当 时, ,
任取 ,则 ,所以, , ,
所以,函数 在 上为增函数,故排除C、D选项.
故选:A.
【题组四 利用单调性解不等式】
1.(2020·四川省绵阳南山中学双语学校高二月考(文))定义在 上的函数 的导函数为 ,且 ,若 ,则不等式 的解集为( )
A. B. C. D.
【答案】A
【解析】构造函数 ,
∵ ,
∴ ,
∴函数 在 上单调递减,
又 ,
∴不等式 的解集为 ,
故选:A.
2.(2020·山西祁县中学高二月考(文))设函数 ,则使得 成立
的 的取值范围是( )
24 π
A. B. C. D.
【答案】D
【解析】 ,所以 , 为 上的偶函数,又 ,当 时, ,故 在 上为增函数.
因 ,由 得到 ,
故 , 或 ,选D.
3.(2020·山东德州·高三二模)已知函数f(x)的定义域为R,且 ,则不等
式 解集为( )
A. B. C. D.
【答案】C
【解析】构造函数 ,则 ,故 在 上为增函数.
又 ,故 即 ,即 .解得 .
故选:C
4.(2020·历下·山东师范大学附中高三月考)已知定义在 上的函数 ,其导函数为 ,若
,且当 时, ,则不等式
的解集为( )
A. B. C. D.
【答案】C
【解析】令 ,则 ,
, , ,为定义在 上的偶函数;
当 时, , 在 上单调递减,
又 为偶函数, 在 上单调递增.
由 得:
,即 ,
,解得: ,即不等式的解集为 .
故选: .
5.(2020·安徽庐阳·合肥一中高三月考(文))已知函数 ,其中e是自然数对
数的底数,若 ,则实数a的取值范围是( )
A. B. C. D.
【答案】B
【解析】由于 ,,则f(﹣x)=﹣x3 +e﹣x﹣ex=﹣f(x),故函数f(x)
为奇函数.
故原不等式f(a﹣1)+f(2a2)≤0,可转化为f(2a2)≤﹣f(a﹣1)=f(1﹣a),即f(2a2)≤f(1﹣
a);
又f'(x)=3x2﹣cosx+ex+e﹣x,由于ex+e﹣x≥2,故ex+e﹣x﹣cosx>0,
所以f'(x)=3x2﹣cosx+ex+e﹣x≥0恒成立,
故函数f(x)单调递增,则由f(2a2)≤f(1﹣a)可得,2a2≤1﹣a,即2a2+a﹣1≤0,解得 ,
故选B.
【题组五 利用单调性比较大小】
1.(2020·广东盐田·深圳外国语学校高三月考)已知函数 是定义在 上的偶函数,且当
时, ,若 , , ,
则a,b,c的大小关系是( )
A. B.
C. D.
【答案】A
【解析】令 ,由 是定义在 上的偶函数,
可得 是定义在 上的奇函数,
又因为 时, ,
所以 在 上是增函数,所以 是定义在 上的增函数,
又由 ,所以 ,
即 .
故选:A.
2.(2020·江苏淮安·高三月考)已知函数 , ,若 , ,
则a,b,c的大小为( )
A. B. C. D.【答案】B
【解析】因为 ,
所以 在 上单调递增,
因为 , , ,
所以 ,
所以 ,
故 .
故选:B.
3.(2020·五华·云南师大附中高三月考(理))已知函数 ,若 ,
, ,则( )
A. B. C. D.
【答案】B
【解析】函数 ,
设 , ,
则 在 恒成立,
函数 在 上单调递增,
,
即函数 在 上单调递增,且 ,又 函数 在 上单调递增,且 ,
函数 ,在 上单调递增,且 ,
又 ,
函数 是偶函数,
, ,
, ,而 , ,
,
又 函数 在 上单调递增,
,
即 ,
故选: .
4.(2020·河南高三其他(理))设 ,则 的大小关系是( )
A. B. C. D.
【答案】B
【解析】设 ,则 ,
当 时, ,故 在 为减函数,
, ,则 ,故 ;又 , ,即 ,故 ,
.
故选: .
5.(2020·江西南昌二中高三月考(文))已知函数 是定义在R上的偶函数,当 时,
,则 , , 的大小关系为( )
A. B. C. D.
【答案】D
【解析】当 时, ,则 ,
所以 在 上单调递增,
由 ,
所以 ,
因为函数 是定义在R上的偶函数,所以 ,
所以 ,
故选:D