专题34正态分布（解析版）_E015高中全科试卷_数学试题_选修3_05.专项训练_专题34正态分布-高中数学新教材人教A版选择性必修配套提升训练

专题34 正态分布 一、单选题 X N4，1 PX 2  1．（2020·山西应县一中高二期中（理））如果随机变量 ，则 等于（ ）（注： P2 X 20.9544 ） A．0.210 B．0.0228 C．0.0456 D．0.0215 【答案】B 【解析】 1 1 1 P(X剟2) [1P(2 X 6)] [1P(42 X�42)] (10.954 8． 2 2 2 4)0.022 故选：B．  N(1,2) P(2)0.8 2．（2020·宜昌天问教育集团高二期末）设随机变量 服从正态分布 ，若 ，则 P(01) 的值为（ ） A．0.2 B．0.3 C．0.4 D．0.6 【答案】B 【解析】  N  1,2 P1 P10.5 随机变量 服从正态分布 ，所以， ， P12 P2P10.80.50.3 ， P01 P120.3 ，故选B． x2 1  i 3．（2020·辽宁沈阳 高二期中）已知两个正态分布密度函数x e 2 i 2 xR,i 1,2 的图 i 2 i 象如图所示，则（ ）,  ,  A． 1 2 1 2 B． 1 2 1 2 ,  ,  C． 1 2 1 2 D． 1 2 1 2 【答案】A 【解析】 x  正态曲线关于 对称，且 越大图象越靠近右边，第一个曲线的均值比第二个图象的均值小，又有  越小图象越瘦高，得到正确的结果． 详解： 1 正态曲线是关于x对称，且在x处取得峰值 2，由图易得  ，故x 的图象更“瘦 1 2 1  x   高”， 2 的图象更“矮胖”，则 1 2.故选A. X  N  3，2 PX 50.2 4．（2020·通榆县第一中学校高二期末（理））若随机变量 且 ，则 P1 X 5 （ ） 0.6 0.5 0.4 0.3 A． B． C． D． 【答案】A 【解析】 N  3,2 随机变量X服从正态分布 ，  该正态曲线的对称轴是x3， P(X 5)0.2  ， P(1 X 5)12PX 510.40.6 . 故选：A． N4,3 P2a3 Pa2 5．（2020·湖北郧阳 高二月考）设随机变量 服从正态分布 ，若 ， a 则 的值为（ ） 7 5 A．3 B．3 C．5 D．3 【答案】D 【解析】  N4,3 P2a3 Pa2 ∵ 服从正态分布 ， ， ∴2a3a242，解得a3． 故选：D． X ~ N2,1 6．（2020·福建高三其他（理））已知随机变量 ，其正态分布密度曲线如图所示，若在边长 OABC 为1的正方形 内随机取一点，则该点恰好取自黑色区域的概率为（ ） ~ N  ,2 P0.6826 附：若随机变量 ，则 ， P220.9544 . 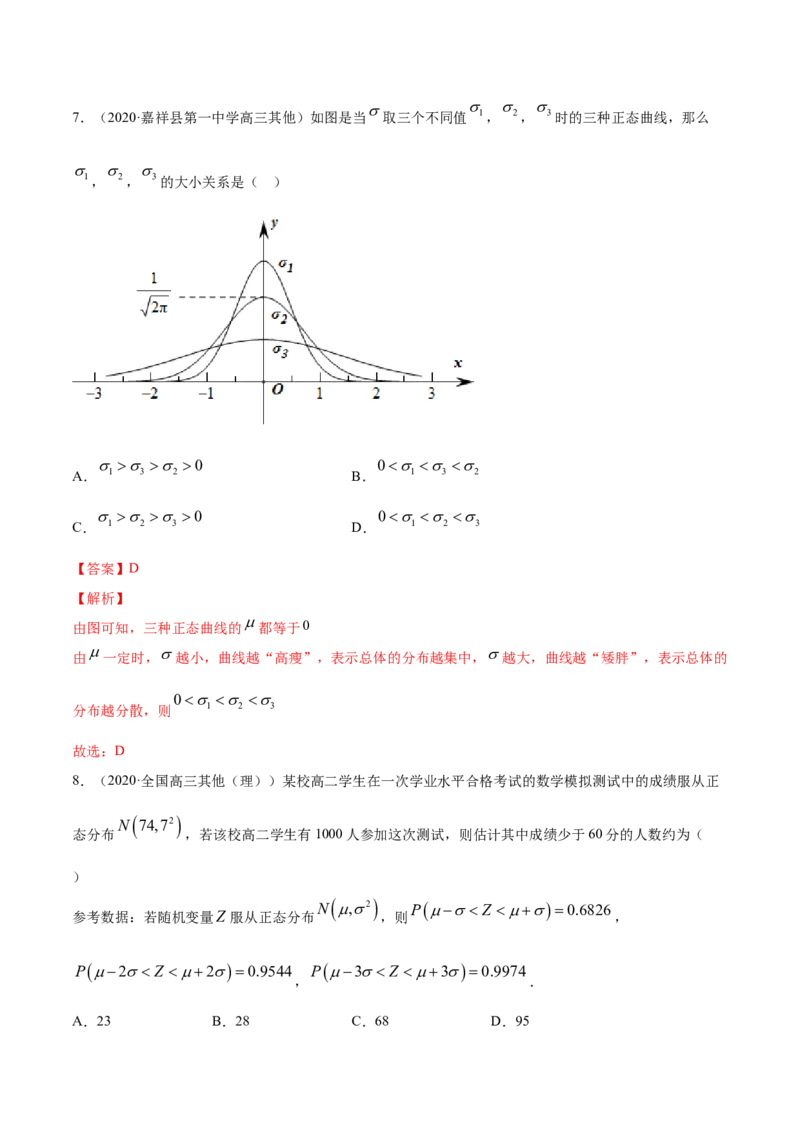A．0.1359 B．0.6587 C．0.7282 D．0.8641 【答案】D 【解析】 X ~ N2,1 因为 1 由题意P 1P(0 X�1)1 0.95440.68260.8641， 阴影 2 故选：D    7．（2020·嘉祥县第一中学高三其他）如图是当 取三个不同值 1， 2， 3时的三种正态曲线，那么    1， 2， 3的大小关系是（ ）    0 0   A． 1 3 2 B． 1 3 2    0 0   C． 1 2 3 D． 1 2 3 【答案】D 【解析】  由图可知，三种正态曲线的 都等于0 由  一定时，越小，曲线越“高瘦”，表示总体的分布越集中，越大，曲线越“矮胖”，表示总体的 0   分布越分散，则 1 2 3 故选：D 8．（2020·全国高三其他（理））某校高二学生在一次学业水平合格考试的数学模拟测试中的成绩服从正 N  74,72 态分布 ，若该校高二学生有1000人参加这次测试，则估计其中成绩少于60分的人数约为（ ） N  ,2 PZ 0.6826 参考数据：若随机变量Z 服从正态分布 ，则 ， P2Z 20.9544 P3Z 30.9974 ， ． A．23 B．28 C．68 D．95【答案】A 【解析】 P2Z 20.9544 由 ，得 P7414 X  P60 X 0.9544 ， 1 PX 60 PX  1P60 X 0.0228   所以 2 ， 10000.022822.823 从而成绩少于60分的人数约为 （人）， 故选：A． 二、多选题 9．（2020·江苏常州 高二期末）已知在某市的一次学情检测中，学生的数学成绩X服从正态分布N(105， 100)，其中90分为及格线，120分为优秀线，下列说法正确的是（ ）   2  22 附：随机变量 服从正态分布N( ， )，则P( )＝0.6826，P( ) 33 ＝0.9544，P( )＝0.9974. A．该市学生数学成绩的期望为105 B．该市学生数学成绩的标准差为100 C．该市学生数学成绩及格率超过0.99 D．该市学生数学成绩不及格的人数和优秀的人数大致相等 【答案】AD 【解析】 105,10,220 285 依题意 ， . 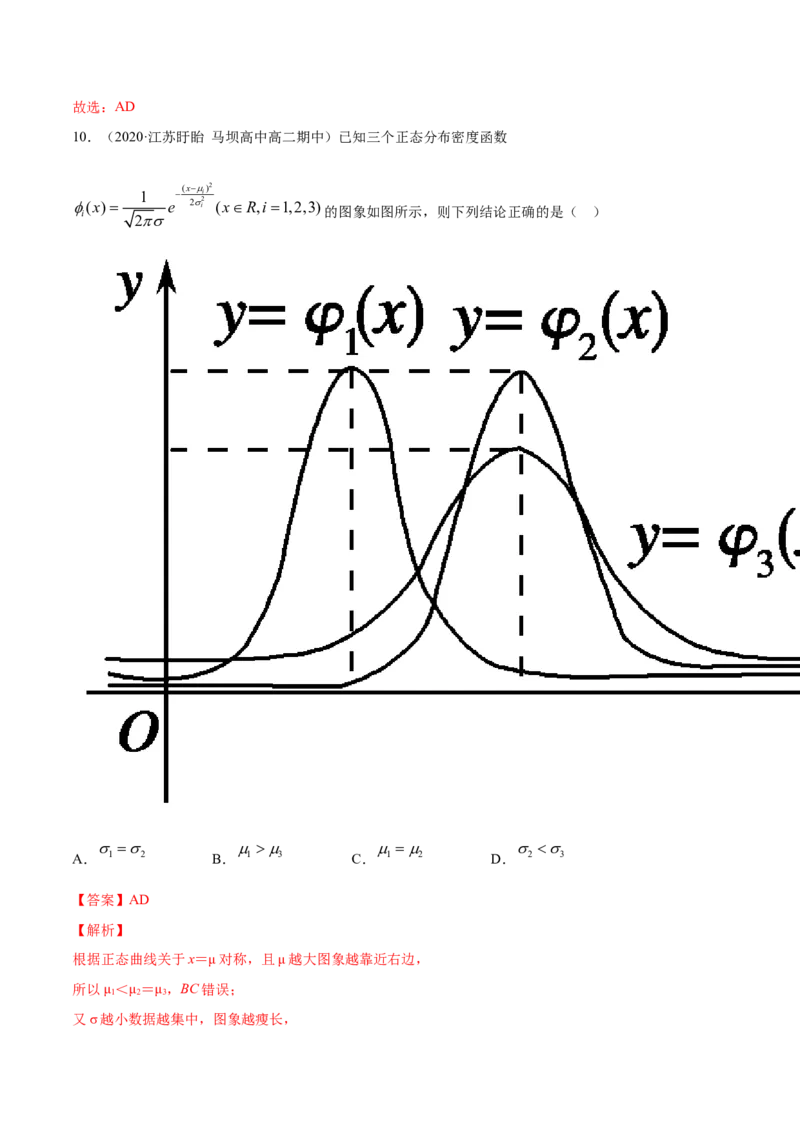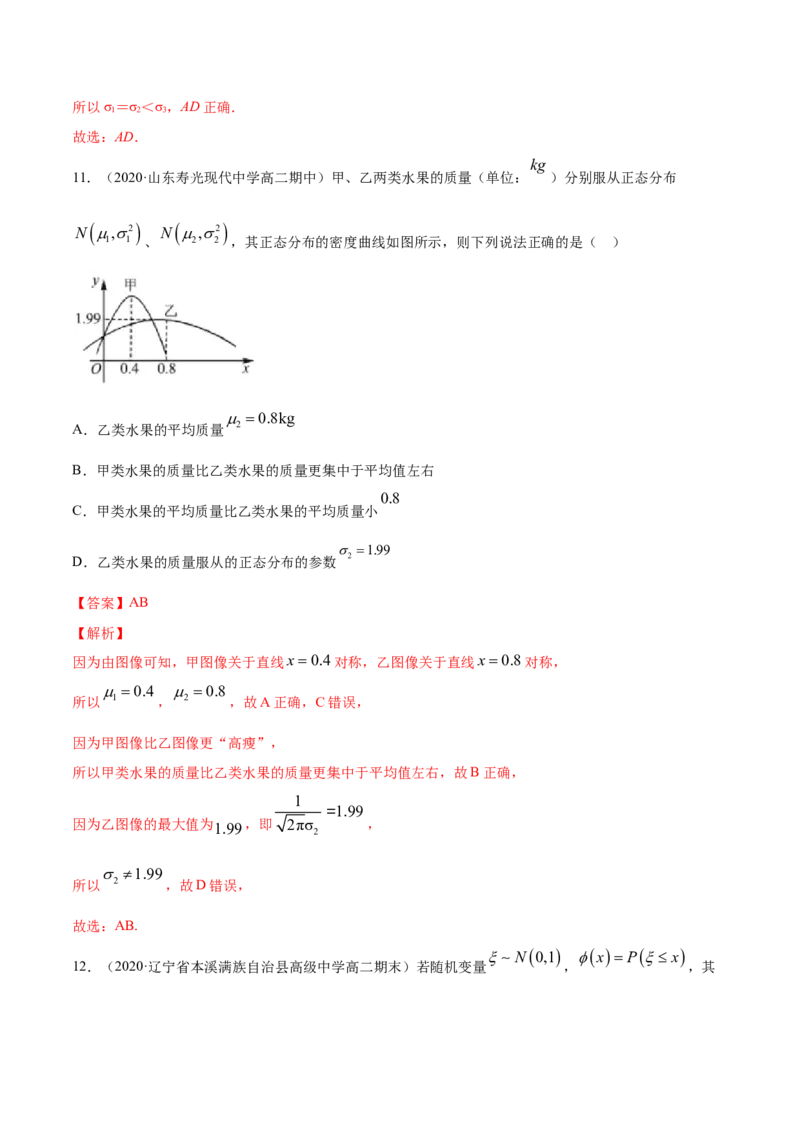期望为105，选项A正确；方差为100，标准差为10，选项B错误； 10.9544 1 0.9772 该市85分以上占 2 ，故C错误； 90120 105 由于 2 ，根据对称性可判断选项D正确.故选：AD 10．（2020·江苏盱眙 马坝高中高二期中）已知三个正态分布密度函数 (x)2 1  i (x) e 2 i 2 (xR,i 1,2,3) 的图象如图所示，则下列结论正确的是（ ） i 2         A． 1 2 B． 1 3 C． 1 2 D． 2 3 【答案】AD 【解析】 根据正态曲线关于x＝μ对称，且μ越大图象越靠近右边， 所以μ＜μ＝μ，BC错误； 1 2 3 又σ越小数据越集中，图象越瘦长，所以σ＝σ＜σ，AD正确． 1 2 3 故选：AD． kg 11．（2020·山东寿光现代中学高二期中）甲、乙两类水果的质量（单位： ）分别服从正态分布 N  ,2 N  ,2 1 1 、 2 2 ，其正态分布的密度曲线如图所示，则下列说法正确的是（ ）  0.8kg A．乙类水果的平均质量 2 B．甲类水果的质量比乙类水果的质量更集中于平均值左右 0.8 C．甲类水果的平均质量比乙类水果的平均质量小  1.99 D．乙类水果的质量服从的正态分布的参数 2 【答案】AB 【解析】 因为由图像可知，甲图像关于直线x0.4对称，乙图像关于直线x0.8对称，  0.4  0.8 所以 1 ， 2 ，故A正确，C错误， 因为甲图像比乙图像更“高瘦”， 所以甲类水果的质量比乙类水果的质量更集中于平均值左右，故B正确， 1 =1.99 因为乙图像的最大值为 1.99 ，即 2πσ ， 2  1.99 所以 2 ，故D错误， 故选：AB. 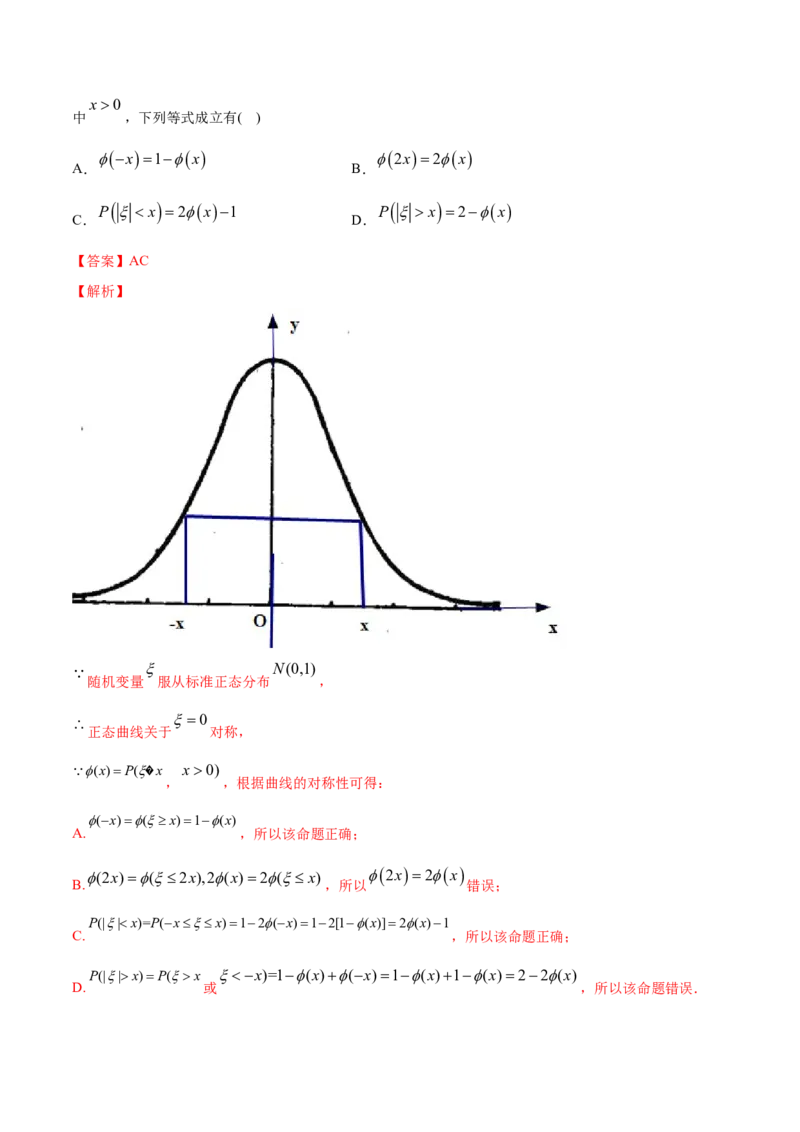 N0,1 x P x  12．（2020·辽宁省本溪满族自治县高级中学高二期末）若随机变量 ， ，其x0 中 ，下列等式成立有( ) x1x 2x2x A． B． P   x  2x1 P   x  2x C． D． 【答案】AC 【解析】  N(0,1) 随机变量 服从标准正态分布 ， 0  正态曲线关于 对称， (x)P(�x x0)  ， ，根据曲线的对称性可得： (x)(x)1(x) A. ，所以该命题正确； (2x)(2x),2(x)2( x) 2x2x B. ，所以 错误； P(||x)=P(xx)12(x)12[1(x)]2(x)1 C. ，所以该命题正确； P(||x)P(x x)=1(x)(x)1(x)1(x)22(x) D. 或 ，所以该命题错误．故选：AC ． 三、填空题 1  (x)2 f(x) e 2 13．（2020·苏州大学附属中学高二月考）正态总体的概率密度函数 ， 的图象 2 xR 关于直线________对称． x 【答案】 【解析】 1  (x)2 f(x) e 2 由正态曲线的特征可知正态总体的概率密度函数 ， 的图象关于直线 对称. 2 xR x x 故答案为： X N  4,32 PX 0 PX a1 14．（2020·营口市第二高级中学高二期末）设随机变量  ，且 ， a 则实数 的值为_______. 【答案】9 【解析】 分析： X N  4,32 随机变量  的正态曲线关于X 4对称，即0与a1关于X 4对称，解出即可． 详解： 根据题意有0a142a9 故填9 15．（2020·全国高三课时练习（理））某个部件由两个电子元件按如图 方式连接而成，元件1或元件2正常工作，则部件正常工作，设两个电子元件的使用寿命(单位：小时)均 服从正态分布N(1 000，502)，且各个元件能否正常工作相互独立．那么该部件的使用寿命超过1 000小时 的概率为_________. 3 【答案】4 . 【解析】解法一：(1)由正态分布知元件，1，2的平均使用寿命为1 000小时，设元件1，2的使用寿命超过1 000小 1 时分别记为事件A，B，显然P(A)＝P(B)＝2 ，所以该部件的使用寿命超过1 000小时的事件为 1 1 1 1 1 1 3       AB AB AB，所以其概率P＝2 2 2 2 2 2 4. 解法二：两个电子元件的使用寿命均服从正态分布N(1 000，502)得两个电子元件的使用寿命超过1 000小 1 3 P P 1(1P)2  时的概率均为 2 ，则该部件使用寿命超过1 000小时的概率为 1 4 . 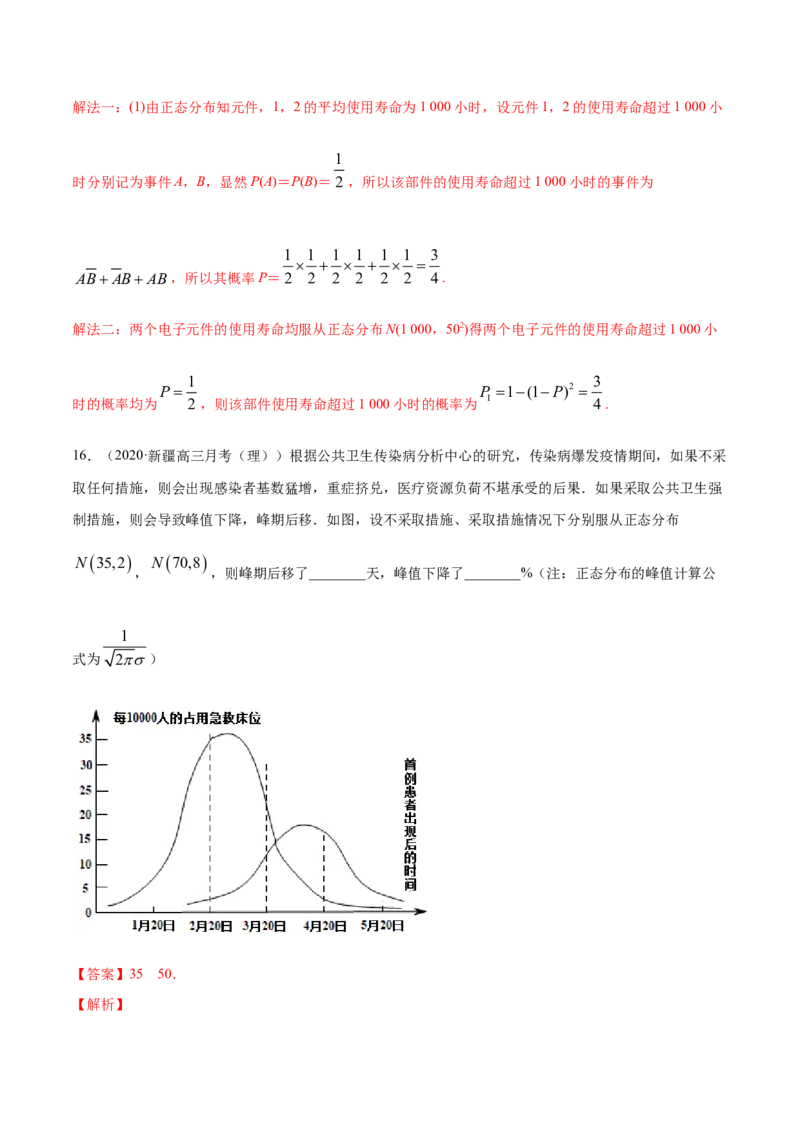16．（2020·新疆高三月考（理））根据公共卫生传染病分析中心的研究，传染病爆发疫情期间，如果不采 取任何措施，则会出现感染者基数猛增，重症挤兑，医疗资源负荷不堪承受的后果．如果采取公共卫生强 制措施，则会导致峰值下降，峰期后移．如图，设不采取措施、采取措施情况下分别服从正态分布 N35,2 N70,8 ， ，则峰期后移了________天，峰值下降了________%（注：正态分布的峰值计算公 1 式为 2） 【答案】35 50． 【解析】703535 （1）由题意可知，峰期后移了 （天）；  1 1  1 1    50%   （2）峰值下降了  2 2 2 8 2 2 2 ． 故答案为：35；50 四、解答题 17．（2019·全国高二课时练习）生产工艺工程中产品的尺寸误差X(单位:mm)~N(0,1.52),如果产品的尺寸与 规定的尺寸偏差的绝对值不超过1.5 mm为合格品,求: (1)X的密度函数; (2)生产的5件产品的合格率不小于80%的概率. 1  x2 x e 4.5 【答案】（1） ；（2） . 1.5 2 0.494 【解析】 X~ N  0,1.52 , (1)由题意知 μ 0,σ1.5 即 , 1 - x2 φx e 4.5. 故密度函数 1.5 2π (2)设Y表示5件产品中的合格品数, P  X 1.5  P1.5X1.50.683 每件产品是合格品的概率为 , Y~ B5,0.683 80% Y50.84 而 ,合格率不小于 ,即 , PY4PY4PY 5C40.683410.6830.6835 0.494. 故 5 18．（2020·山西迎泽 太原五中高三二模（理））《山东省高考改革试点方案》规定：从2017年秋季高中 入学的新生开始，不分文理科；2020年开始，高考总成绩由语数外3门统考科目和物理、化学等六门选考 科目构成．将每门选考科目的考生原始成绩从高到低划分为A、B、B、C、C、D、D、E共 3% 7% 16% 24% 24% 16% 8个等级．参照正态分布原则，确定各等级人数所占比例分别为 、 、 、 、 、 、7%、3%．选考科目成绩计入考生总成绩时，将A至E等级内的考生原始成绩，依照等比例转换法则， [91,100] [81,90] [71,80] [61,70] [51,60] [41,50] [31,40] [21,30] 分别转换到 、 、 、 、 、 、 、 八个分数区 间，得到考生的等级成绩．某校高一年级共2000人，为给高一学生合理选科提供依据，对六个选考科目进 N(60,169) 行测试，其中物理考试原始成绩基本服从正态分布 ． (47,86) （1）求物理原始成绩在区间 的人数； X [61,80] （2）按高考改革方案，若从全省考生中随机抽取3人，记 表示这3人中等级成绩在区间 的人数， 求X 的分布列和数学期望． ~ N  ,2 P()0.682 P(22)0.954 （附：若随机变量 ，则 ， ， P(33)0.997 ） 【答案】（Ⅰ）1636人；（Ⅱ）见解析． 【解析】  N  60,132 （Ⅰ）因为物理原始成绩 ， P(4786) P(4760)P(6086) 所以 1 1  P(60136013) P(6021360213) 2 2 0.682 0.954   2 2 0.818． 20000.8181636 所以物理原始成绩在（47，86）的人数为 （人）． 2 （Ⅱ）由题意得，随机抽取1人，其成绩在区间[61,80]内的概率为5 ．  2 X B 3,   所以随机抽取三人，则 X 的所有可能取值为0,1,2,3，且  5，3 3 27 PX 0  所以   ， 5 125 2 2 3 54 PX 1C1   3 5  5   125 ， 2 2 3 36 PX 2C2   3  5   5 125 ， 3 2 8 PX 3    ． 5 125 所以X 的分布列为 X 0 1 2 3 27 54 36 8 P 125 125 125 125 2 6 EX3  所以数学期望 5 5 ． 19．（2020·陕西西安 高三月考（理））为调查某校学生每周体育锻炼落实的情况，采用分层抽样的方法， h 收集100位学生每周平均锻炼时间的样本数据(单位: ).根据这100个样本数据，制作出学生每周平均锻炼 时间的频率分布直方图(如图所示).x s2 （Ⅰ）估计这100名学生每周平均锻炼时间的平均数 和样本方差 (同一组中的数据用该组区间的中点 值作代表)； （Ⅱ）由频率分布直方图知，该校学生每周平均锻炼时间Z 近似服从正态分布 N  ,2 ，其中  近似为 x 2 s2 样本平均数 ， 近似为样本方差 . P(0.8Z 8.3) （i）求 ； (0.8,8.3)  E() （ii）若该校共有5000名学生，记每周平均锻炼时间在区间 的人数为 ，试求 . 附： 6.16 2.5，若Z ~ N  ,2 ， P(Z )0.6827 ， P(2Z 2)0.9545 . 0.8186 4093 【答案】（Ⅰ）平均数5.85；样本方差6.16；（Ⅱ）（i） ；（ii） . 【解析】 （Ⅰ）这100名学生每周平均锻炼时间的平均数为 x10.0530.250.370.2590.15110.055.8 .s2 (15.8)20.05(35.8)20.2(55.8)20.3(75.8)20.25(95.8)20.15(115.8)20.05 6.16 . Z ~ N(5.8,6.16) （Ⅱ）（i）由（Ⅰ）知 ， Z ~ N  5.8,2.52 即 ， P(0.8Z 8.3) P(5.85 Z 5.82.5) P(2 Z ) 从而 1  P(Z ) [P(2 Z 2)P( Z )]0.8186 2 （ii）由（i）可 ~ B(5000,0.8186) 知， ， E()np 50000.81864093 故 . 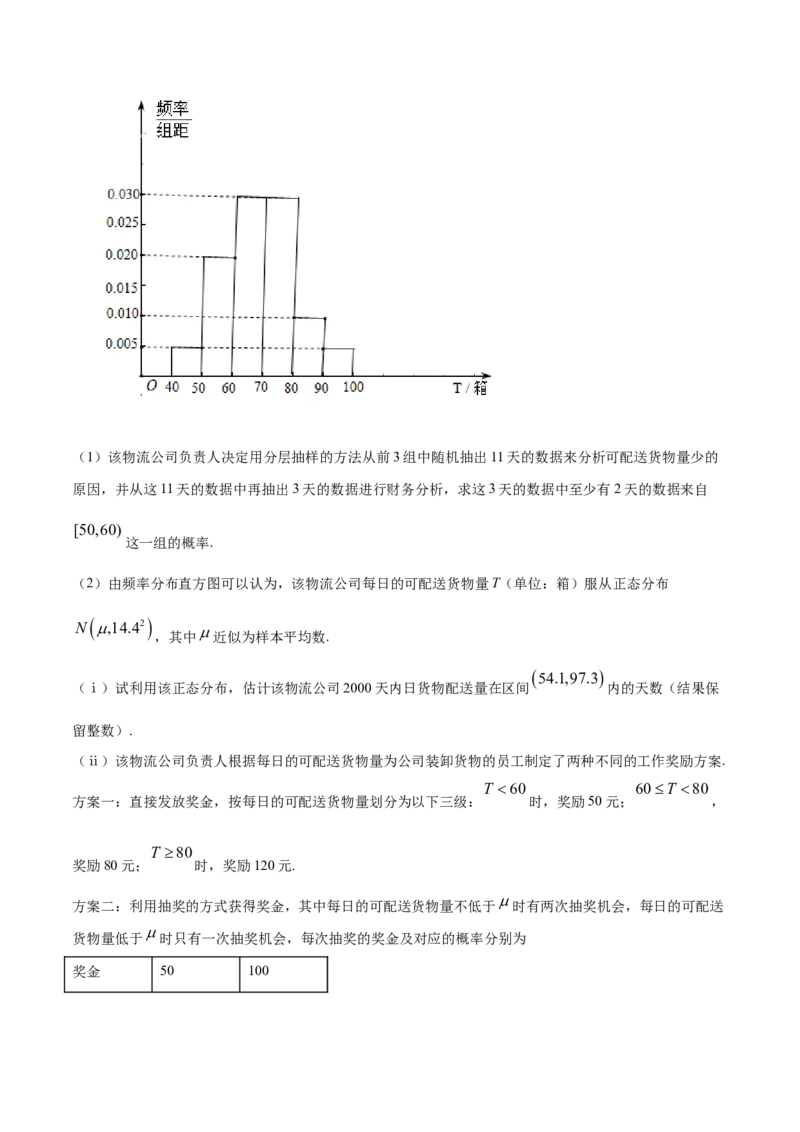20．（2020·湖北黄石港 黄石二中高二月考（理））某物流公司专营从甲地到乙地的货运业务（货物全部 用统一规格的包装箱包装），现统计了最近100天内每天可配送的货物量，按照可配送货物量T（单位： [40,50) [50,60) [60,70) [70,80) [80,90) [90,100] 箱）分成了以下几组： ， ， ， ， ， ，并绘制了如图所 示的频率分布直方图（同一组数据用该组数据的区间中点值作代表，将频率视为概率）.（1）该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的 原因，并从这11天的数据中再抽出3天的数据进行财务分析，求这3天的数据中至少有2天的数据来自 [50,60) 这一组的概率. （2）由频率分布直方图可以认为，该物流公司每日的可配送货物量T（单位：箱）服从正态分布 N  ,14.42  ，其中 近似为样本平均数. 54.1,97.3 （ⅰ）试利用该正态分布，估计该物流公司2000天内日货物配送量在区间 内的天数（结果保 留整数）. （ⅱ）该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案. T 60 60T 80 方案一：直接发放奖金，按每日的可配送货物量划分为以下三级： 时，奖励50元； ， T 80 奖励80元； 时，奖励120元.  方案二：利用抽奖的方式获得奖金，其中每日的可配送货物量不低于 时有两次抽奖机会，每日的可配送  货物量低于 时只有一次抽奖机会，每次抽奖的奖金及对应的概率分别为 奖金 50 1004 1 概率 5 5 小张恰好为该公司装卸货物的一名员工，试从数学期望的角度分析，小张选择哪种奖励方案对他更有利？ Z ~ N  ,2 P(Z )0.6827 P(2Z 2)0.9545 附：若 ，则 ， . 46 【答案】（1）165（2）（ⅰ）1637天（ⅱ）小张选择方案二更有利 【解析】 （1）由分层抽样知识可知，这11天中前3组的数据分别有1个，4个，6个， C2C1 C3 46 P 4 7  4  所以至少有2天的数据来自[50,60)这一组的概率概率为 C3 C3 165. 11 11 450.05550.2650.3750.3850.1950.0568.5 （2）（ⅰ）由题得 ， 1 P(54.1T 97.3) P(68.514.4T 68.5 28. 8) (0.68270.9545)0.8186 所以 2 . 54.1,97.3 2 000 0.81861637.21637 故2000天内日货物配送量在区间 内的天数为 . 1 P(T ) P(T ) （ⅱ）易知 2. 对于方案一，设小张每日可获得的奖金为X 元，则X 的可能取值为50，80，120， 其对应的概率分别为0.25，0.6，0.15， E(X)500.25800.61200.1578.5 故 . 对于方案二，设小张每日可获得的奖金为Y 元，则Y 的所有可能取值为50，100，150，200， 1 4 2 1 1 1 4 4 21 P(Y 50)   P(Y 100)      故 2 5 5， 2 5 2 5 5 50 ， 1 1 4 4 1 1 1 1 P(Y 150)2    P(Y 200)    2 5 5 25， 2 5 5 50. 所以Y 的分布列为 Y 50 100 150 2002 21 4 1 P 5 50 25 50 2 21 4 1 E(Y)50 100 150 200 90 所以 5 50 25 50 . E(Y) E(X) 因为 ， 所以从数学期望的角度看，小张选择方案二更有利. n 21．（2020·河北易县中学高三其他（理））某精密仪器生产车间每天生产 个零件，质检员小张每天都会 随机地从中抽取50个零件进行检查是否合格，若较多零件不合格，则需对其余所有零件进行检查．根据多 N(10,0.12) m 年的生产数据和经验，这些零件的长度服从正态分布 （单位：微米 ），且相互独立．若零 d 9.7md 10.3m 件的长度 满足 ，则认为该零件是合格的，否则该零件不合格． P(X ≥2) X X EX （1）假设某一天小张抽查出不合格的零件数为 ，求 及 的数学期望 ； （2）小张某天恰好从50个零件中检查出2个不合格的零件，若以此频率作为当天生产零件的不合格率． n 已知检查一个零件的成本为10元，而每个不合格零件流入市场带来的损失为260元．假设 充分大，为了 使损失尽量小，小张是否需要检查其余所有零件，试说明理由．  N(,2) 附：若随机变量 服从正态分布 ，则 P(33)0.9987,0.998750 0.9370,0.9987490.00130.0012 ． 【答案】（1）见解析（2）需要，见解析 【解析】 P(X ≥2)1P(X 1)P(X 0)1C 10.9987490.00130.998750 0.003 （1） 50 , X EX 0.0013500.065 由于 满足二项分布,故 . 2 （2）由题意可知不合格率为50,2 52 E(Y)260n 20 n20 若不检查,损失的期望为 50 5 ； 52 2 E(Y)10n n2010n n20 若检查,成本为10n,由于 5 5 , 2 E(Y)10n n200 当n充分大时, 5 , 所以为了使损失尽量小,小张需要检查其余所有零件. 22．（2020·定西市第一中学高三其他（理））在创建“全国文明城市”过程中，银川市“创城办”为了调查市 民对创城工作的了解情况，进行了一次创城知识问卷调查（一位市民只能参加一次）通过随机抽样，得到 参加问卷调查的100人的得分统计结果如表所示： 组别 [30，40) [40，50) [50，60) [60，70) [70，80) [80，90) [90，100] 频数 2 13 21 25 24 11 4 （1）由频数分布表可以大致认为，此次问卷调查的得分Z~N(μ，198)，μ近似为这100人得分的平均值 （同一组中的数据用该组区间的左端点值作代表）， ①求μ的值； P(Z 88.5) ②利用该正态分布，求 ； （2）在（1）的条件下，“创城办”为此次参加问卷调查的市民制定如下奖励方案：   ①得分不低于 的可以获赠2次随机话费，得分低于 的可以获赠1次随机话费； ②每次获赠的随机话费和对应的概率为： 赠送话费的金额（单元：元） 20 50 3 1 概率 4 4 现有市民甲参加此次问卷调查，记X （单位：元）为该市民参加问卷调查获赠的话费，求X 的分布列与 数学期望． 参考数据与公式： 198 14．若 X  N  ,2 ，则 P X 0.6826 ， P2 X 20.9544 P3 X 30.9974 ， ．165 【答案】（1）①60.5②0.0228（2）见解析， 4 【解析】 30240135021602570248011904 60.5 （1）由题意得： 100 ， 60.5  198 14 ∴ ，∵ ， 1P(u2Z 2) P(Z 88.5) P(Z 2) 0.0228 2 ， 1 PZ  PZ  （2）由题意知 2，. 获赠话费X 的可能取值为20，40，50，70，100， 1 3 3 1 3 3 9 1 1 1 PX 20   PX 40    PX 50   2 4 8， 2 4 4 32 ， 2 4 8 ， 1 3 1 1 1 3 3 1 1 1 1 PX 70       PX 100    2 4 4 2 4 4 16 ， 2 4 4 32，. ∴X 的分布列为： X 20 40 50 70 100 3 9 1 3 1 P 8 32 8 16 32 3 9 1 3 1 165 E(X)20 40 50 70 100  ∴ 8 32 8 16 32 4 .