文档内容
专题 13 预备知识十三:幂函数
1、通过具体实例,了解幂函数的定义,会画 , , , , 五个幂函数的图
象,理解它们的性质;
2、通过对幂函数的研究,体会研究一类函数的基本内容与方法.
知识点一:幂函数的概念
1、定义:一般地,函数 叫做幂函数,其中 是自变量, 是常数.
2、幂函数的特征
① 中 前的系数为“1”
② 中 的底数是单个的自变量“ ”
③ 中 是常数
知识点二:幂函数的图象与性质
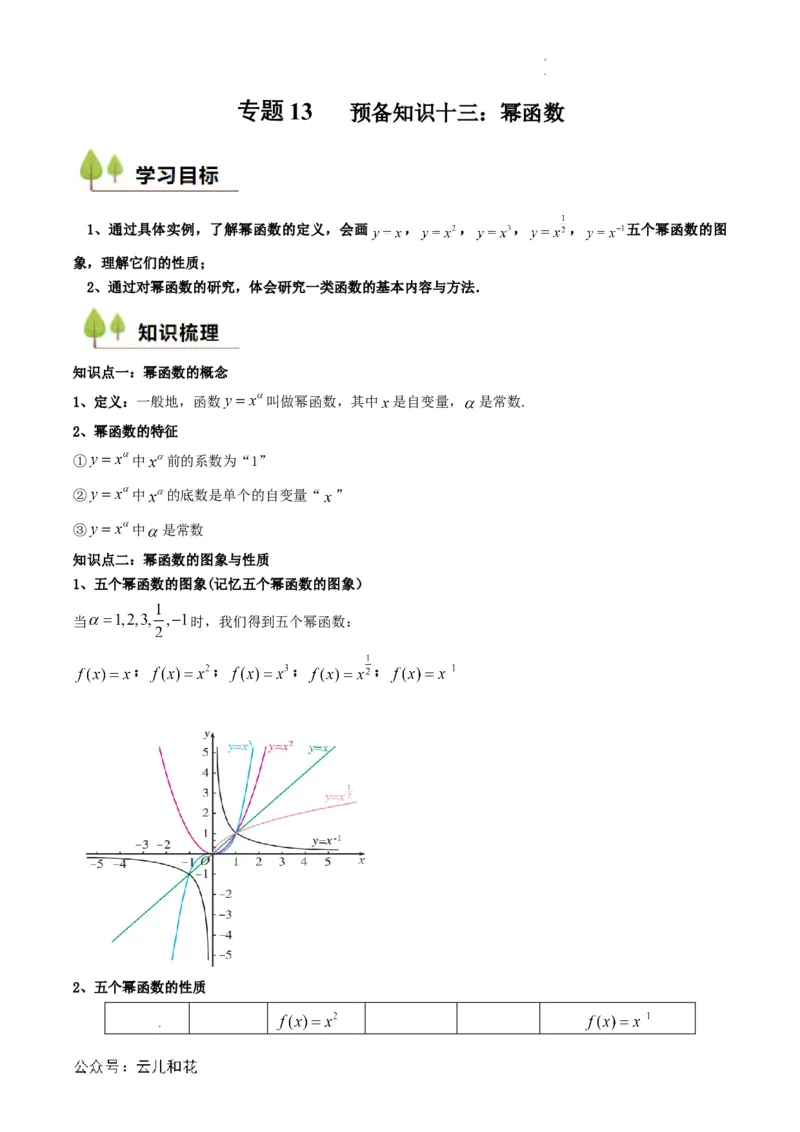
1、五个幂函数的图象(记忆五个幂函数的图象)
当 时,我们得到五个幂函数:
; ; ; ;
2、五个幂函数的性质
学科网(北京)股份有限公司 学科网(北京)股份有限公司定义域
值域
奇偶性 奇函数 偶函数 奇函数 非奇非偶 奇函数
在 上
在 上单 单调递减 在 上单调 在 在 上单调递减
单调性
调递增 在 单 递增 单调递增 在 上单调递减
调递增
定点
3、拓展:
① ,当 时, 在 单调递增;
② ,当 时, 在 单调递减.
对点特训一:求幂函数的值
典型例题
例题1.(2024高三·全国·专题练习)若幂函数 的图象经过点 ,则 =( )
A. B.2 C.4 D.
【答案】C
【分析】利用已知条件求得幂函数解析式,然后代入求解即可.
【详解】设幂函数 ,因为 的图象经过点 ,所以 ,解得 ,
所以 ,所以 .
故选:C
例题2.(23-24高一上·山东聊城·期末)已知幂函数 的图象通过点 ,则 .
【答案】 /0.5
【分析】由幂函数的定义,结合函数过 求得函数解析式,进而可得 的值.
【详解】设幂函数 的解析式为
学科网(北京)股份有限公司 学科网(北京)股份有限公司∵幂函数 过点
∴
∴
∴该函数的解析式为 ,
∴ .
故答案为:
精练
1.(23-24高一上·广东茂名·期末)已知幂函数 ,则 ( )
A. B.1 C. D.2
【答案】A
【分析】根据函数为幂函数得到方程,求出 ,得到解析式,代入求值即可.
【详解】因为 是幂函数,所以 ,即 ,
所以 , .
故选:A.
2.(23-24高一下·广西南宁·开学考试)已知函数 是幂函数,则 .
【答案】4
【分析】根据幂函数的定义求出参数 的值,即可得到函数解析式,再代入计算可得.
【详解】因为函数 是幂函数,
所以 ,解得 , , .
故答案为:
对点特训二:求幂函数的解析式
典型例题
例题1.(23-24高一下·黑龙江哈尔滨·开学考试)幂函数 在 上是减函数,
则实数 的值为( )
A.2或 B. C.2 D. 或
【答案】B
【分析】根据幂函数解析式的特征,以及幂函数的性质,即可求解 的值.
【详解】由题意可知, ,解得: 或 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司当 时, ,函数在 上是减函数,成立,
当 时, ,函数在 上是增函数,不成立,
所以 .
故选:B
例题2.(23-24高一下·辽宁·阶段练习)已知幂函数 的图象与坐标轴无交点.
(1)求 的解析式;
(2)解不等式 .
【答案】(1) ;
(2) 且 .
【分析】(1)利用幂函数的定义,结合图象特征求出 即得.
(2)由幂函数的单调性结合奇偶性求解不等式.
【详解】(1)由 是幂函数,得 ,解得 或 ,
由 的图象与坐标轴无交点,得 ,则 ,
所以 的解析式是 .
(2)显然函数 是偶函数,且在 上单调递减,
不等式 ,
因此 ,解得 且 ,
所以原不等式的解集为 且 .
精练
1.(23-24高一上·安徽马鞍山·期中)已知幂函数 满足①函数图象不经过原点;②
,写出符合上述条件的一个函数解析式 .
【答案】 (答案不唯一)
【分析】本题根据幂函数的概念,结合题目给的限制性条件即可找到符合条件的函数.
【详解】因为 对 ,则 在 上为减函数,
又因为幂函数 ( 为常数),当 不经过原点时, 即可,
故可取 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司故答案为: (答案不唯一).
2.(23-24高一上·辽宁朝阳·期末)已知幂函数 的图像关于 轴对称,则 .
【答案】1
【分析】由幂函数和偶函数的性质求解即可.
【详解】由于函数是幂函数,所以 ,解得 或 .
当 时, ,是奇函数,图象不关于 轴对称;
当 时, ,是偶函数,图象关于 轴对称,符合题意,所以 的值为1.
故答案为: .
对点特训三:求幂函数的值域
典型例题
例题1.(23-24高一上·陕西商洛·期中)已知幂函数 满足:
① 在 上为增函数,
②对 ,都有 ,
求同时满足①②的幂函数 的解析式,并求出 时, 的值域.
【答案】 ,
【分析】利用幂函数的性质及题设条件可确定 表达式,进而确定其在指定区间上的值域.
【详解】因为 在 上为增函数,所以 ,解得 ,
又 ,所以, 或 .
又因为 ,所以 是偶函数,所以 为偶数.
当 时, 满足题意;当 时, 不满足题意,
所以 ,
又因为 在 上递增,所以 , ,
故 时, 的值域是 .
例题2.(2024高一·全国·课后作业)已知幂函数 ,其中 ,满足:
①在区间 上单调递增;
②对任意的 ,都有 .
求同时满足条件①②的幂函数 的解析式,并求 时 的值域.
【答案】 ,值域为
学科网(北京)股份有限公司 学科网(北京)股份有限公司【分析】先根据幂函数的性质求出 , ,再根据单调性可得 的值域.
【详解】因幂函数 在区间 为增函数,
则 ,即 ,
解得: ,
又因 ,所以 或 ,
当 时, 为偶函数,不满足 ;
当 时, 为奇函数,满足 ;
故 ,
当 时, ,
即函数 的值域 .
精练
1.(23-24高一·全国·课后作业)已知幂函数 的图象经过点 .
(1)求函数 的解析式;
(2)设函数 ,求函数 在区间 , 上的值域.
【答案】(1) , ;(2) .
【解析】(1)设出函数的解析式,代入点的坐标,求出函数的解析式即可;
(2)求出 的解析式,根据函数的单调性求出函数的值域即可.
【详解】解:设函数的解析式为 ,
则 ,解得: ,
故 , ;
(2)由(1) ,
在 递增,
故 ,
,
故函数的值域是 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司【点睛】本题考查了幂函数的定义,考查函数的值域以及函数的单调性问题,属于基础题.
2.(23-24高一上·山东泰安·阶段练习)已知幂函数 (其中 , )满足:
①在区间 上为减函数;
②对任意的 ,都有 .
求幂函数 的解析式,并求当 时, 的值域.
【答案】 ,值域为
【解析】根据条件分析 ,0,1,依次检验①②,即可得解.
【详解】解: , , ,0,1.
对任意 ,都有 ,即 , 是偶函数.
当 时, ,满足条件①②;
当 时, ,不满足条件①;
当 时, ,条件①②都不满足,故同时满足条件①②的幂函数 的解析式为 ,
且在区间 上是增函数, 当 时,函数 的值域为 .
【点睛】此题考查根据幂函数的概念结合单调性和奇偶性求函数解析式,根据函数解析式求函数值域.
对点特训四:幂函数的图象问题
典型例题
例题1.(2024·四川南充·二模)已知函数 的图象如图所示,则 的解析式可能是( )
A. B. C. D.
【答案】D
【分析】根据幂函数的性质一一判断即可.
【详解】对于A:函数 的定义域为 ,显然不符合题意,故A错误;
对于B:函数 的定义域为 ,显然不符合题意,故B错误;
学科网(北京)股份有限公司 学科网(北京)股份有限公司对于C:函数 的定义域为 ,又 为奇函数,又 在 上函数是下凸递增,故不符合题
意,故C错误;
对于D:函数 的定义域为 ,又 为奇函数,且 在 上函数是上凸递增,故D
正确.
故选:D
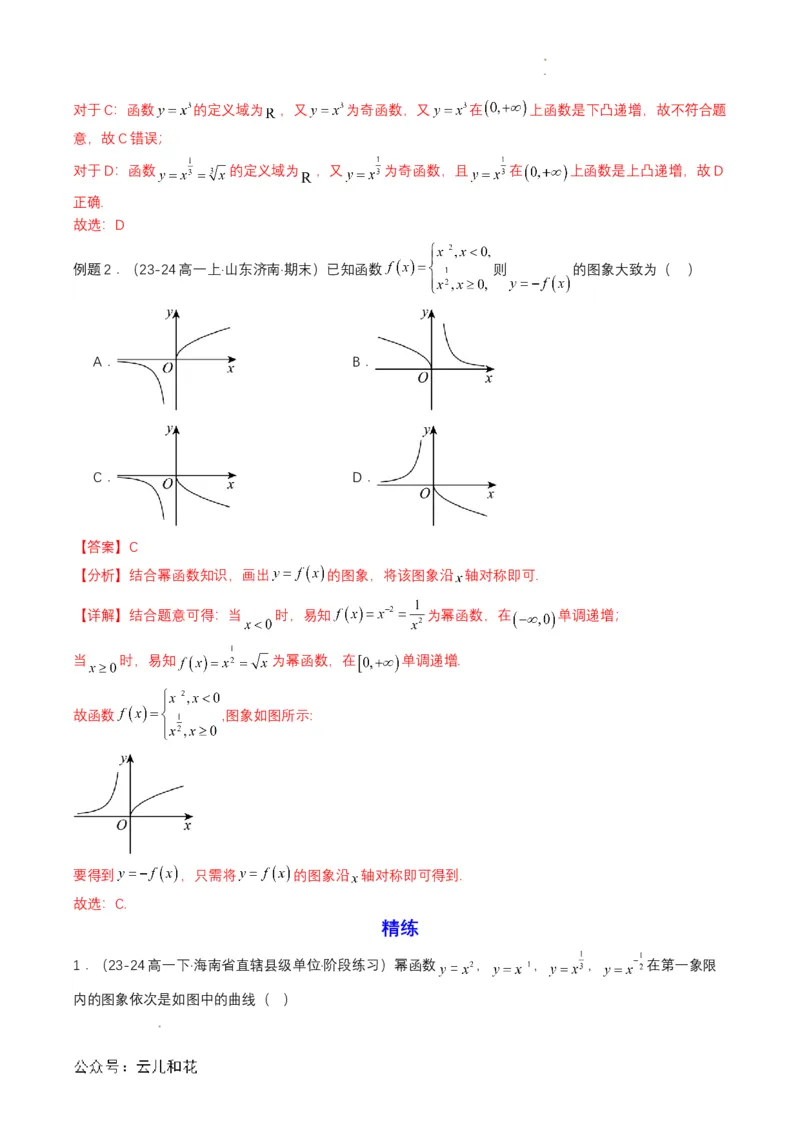
例题2.(23-24高一上·山东济南·期末)已知函数 则 的图象大致为( )
A. B.
C. D.
【答案】C
【分析】结合幂函数知识,画出 的图象,将该图象沿 轴对称即可.
【详解】结合题意可得:当 时,易知 为幂函数,在 单调递增;
当 时,易知 为幂函数,在 单调递增.
故函数 ,图象如图所示:
要得到 ,只需将 的图象沿 轴对称即可得到.
故选:C.
精练
1.(23-24高一下·海南省直辖县级单位·阶段练习)幂函数 , , , 在第一象限
内的图象依次是如图中的曲线( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. , , , B. , , ,
C. , , , D. , , ,
【答案】D
【分析】根据幂函数的性质即可求解.
【详解】根据幂函数 的性质可知,在第一象限内的图像,当 时,图像递增,
且 越大,图像递增速度越快,由此可判断 是曲线 , 是曲线 ;
当 时,图像递减,且 越大,图像越陡,由此可判断 是曲线 ,
是曲线 ;综上所述幂函数 , , , ,
在第一象限内的图象依次是如图中的曲线 , , , .
故选:D.
2.(23-24高一上·上海闵行·期末)如图为三个幂函数 在其定义域上的局部图像,则
实数 从小到大的排列顺序为 .(请用“ ”连接)
【答案】
【分析】利用幂函数的性质判断 的大小即可得解.
【详解】对于 ,由其图象可知 ,例如 ;
对于 ,由其图象可知 ,例如 ;
对于 ,由其图象可知 ,例如 ;
所以 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司故答案为: .
对点特训五:幂函数图象过定点问题
典型例题
例题1.(23-24高一上·上海浦东新·阶段练习)幂函数 的图象不可能在第四象限,但所有图象过定点,
定点坐标为 .
【答案】
【分析】根据幂函数的图象与性质,直接求出定点坐标即得.
【详解】因为对任意实数 ,当 时, ,
所以所有幂函数的图象都过点 .
故答案为:
例题2.(23-24高一上·福建莆田·期中)已知函数 的图象恒过定点 ,若点 在一次函数
的图象上,其中 , ,则 的最小值为 .
【答案】4
【分析】求出函数 的图象恒过定点 ,得到 ,使用基本不等式求 的最小值.
【详解】函数 的图象恒过定点 ,所以 ,
因为 ,所以 ,
当 时, 的最小值为4.
故答案为:4
精练
1.(22-23高一上·上海静安·期中)不论实数 取何值,函数 恒过的定点坐标是 .
【答案】
【分析】根据 ,即可知 恒过定点 .
【详解】因为 ,故当 ,即 时, ,
即函数 恒过定点 .
故答案为: .
2.(20-21高一·全国·课后作业)函数 的图象过定点 .
【答案】
【分析】由幂函数 的图象过 ,将 代入 ,可求出答案.
学科网(北京)股份有限公司 学科网(北京)股份有限公司【详解】幂函数 的图象过 ,
将 代入 ,可得 ,
所以函数 的图象过定点 .
故答案为: .
【点睛】本题考查函数图象过定点问题,注意利用幂函数过定点 的性质,属于基础题.
对点特训六:幂函数的单调性及其应用
典型例题
例题1.(23-24高一上·浙江温州·期中)已知函数 是幂函数,对任意 ,
,且 ,满足 ,若a, ,且 ,则 的值
( )
A.恒大于0 B.恒小于0 C.等于0 D.无法判断
【答案】A
【分析】先通过函数 是幂函数以及单调性求出 的解析式,再利用单调性和奇偶性可得答案.
【详解】因为函数 是幂函数,
所以 ,解得 或 ,
又因为对任意 ,且 ,满足 ,
即对任意 ,都有 ,
故函数 是幂函数且在 上单调递增,
所以 ,
所以 ,
则 ,明显 为 上的奇函数,
由 得 ,
所以 ,
所以 .
故选:A.
例题2.(23-24高一上·江西·阶段练习)已知幂函数 ( )的图像关于 轴对称,且
.
(1)求 的值及函数 的解析式;
(2)若 ,求实数 的取值范围.
学科网(北京)股份有限公司 学科网(北京)股份有限公司【答案】(1) ;(2) .
【解析】(1)由 ,得到函数在区间 为单调递增函数,即 求解.
(2)根据函数 图象关于 轴对称,且在区间 为单调递增函数,将不等式
,转化为 求解.
【详解】(1)由题意,函数 ( )的图像关于 轴对称,且 ,
所以在区间 为单调递增函数,
所以 ,解得 ,
由 , 。
又函数 的图像关于 轴对称,
所以 为偶数,
所以 ,
所以 .
(2)因为函数 图象关于 轴对称,且在区间 为单调递增函数,
所以不等式 ,等价于 ,
解得 或 ,
所以实数 的取值范围是 .
【点睛】本题主要考查幂函数的图象和性质以及函数奇偶性和单调性的应用,还考查了运算求解的能力,
属于中档题.
精练
1.(23-24高二·浙江·期末)已知函数 是幂函数,对任意的 且 ,
满足 ,若 ,则 的值( )
A.恒大于0 B.恒小于0
C.等于0 D.无法判断
【答案】B
【解析】根据函数为幂函数以及函数在 的单调性,可得 ,然后可得函数的奇偶性,结合函数的单
调性以及奇偶性,可得结果.
【详解】由题可知:函数 是幂函数
则 或
学科网(北京)股份有限公司 学科网(北京)股份有限公司又对任意的 且 ,满足
所以函数 为 的增函数,故
所以 ,又 ,
所以 为 单调递增的奇函数
由 ,则 ,所以
则
故选:B
【点睛】本题考查幂函数的概念以及函数性质的应用,熟悉函数单调递增的几种表示,比如
,属中档题.
2.(23-24高一上·安徽马鞍山·期中)已知幂函数 满足①函数图象不经过原点;②
,写出符合上述条件的一个函数解析式 .
【答案】 (答案不唯一)
【分析】本题根据幂函数的概念,结合题目给的限制性条件即可找到符合条件的函数.
【详解】因为 对 ,则 在 上为减函数,
又因为幂函数 ( 为常数),当 不经过原点时, 即可,
故可取 .
故答案为: (答案不唯一).
对点特训七:幂函数的奇偶性
典型例题
例题1.(23-24高三上·上海浦东新·期中)已知 ,若幂函数 为奇函
数,且在 上严格单调递减,则 .
【答案】 或
【分析】由题意,结合幂函数的性质即可求解.
【详解】由幂函数的性质知, ,在第一象限内,当 时,函数单调递减,当 为奇数时,函
数为奇函数,
所以当 或 时,幂函数在 上单调递减,且为奇函数.
故答案为: 或
学科网(北京)股份有限公司 学科网(北京)股份有限公司例题2.(23-24高一上·河北石家庄·阶段练习)已知幂函数 为偶函数,
且在 上单调递减.
(1)求m和k的值;
(2)求满足 的实数a的取值范围.
【答案】(1) , 或 ;
(2)
【分析】(1)根据函数为幂函数,列式计算,即可求得k的值;根据幂函数的单调性求得m的值,结合
奇偶性即可确定m的取值.
(2)结合(1)可得 ,即为 ,利用幂函数的性质,分类求解不等
式,即可求得答案.
【详解】(1)由函数 为幂函数,
则 ,解得 或 ;
由 在 上单调递减,
得 ,解得 ,而 ,故 或2,
当 时, ,定义域为 ,且为偶函数,符合题意;
当 时, ,定义域为 ,函数为奇函数,不符合题意;
故 , 或 ;
(2)结合(1)可知 ,即为 ,
故 或 或 ,
解得 或 或 ,
故实数a的取值范围为 .
精练
1.(23-24高一上·河南·阶段练习)已知 ,若幂函数 为偶函数,且在
上单调递减,则 的取值集合是 .
【答案】
【分析】根据幂函数的性质得到 ,再结合函数的奇偶性求出答案.
【详解】因为幂函数 在 上单调递减,所以 ,
当 时, ,定义域为 ,又 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司故 为奇函数,舍去;
当 时, ,定义域为 ,又 ,
故 为奇函数,舍去;
当 时, ,定义域为 ,又 ,
故 为偶函数,满足要求,
当 时, ,定义域为 ,故不为偶函数,舍去.
故答案为:
2.(23-24高一上·安徽阜阳·期中)已知函数 是幂函数,且函数 的图象关于
轴对称.
(1)求实数 的值;
(2)若不等式 成立,求实数 的取值范围.
【答案】(1)
(2)
【分析】(1)根据幂函数的定义和性质运算求解;
(2)根据 的定义域以及单调性分析求解.
【详解】(1)因为函数 是幂函数,
则 ,即 ,解得 或1,
又因为函数 关于 轴对称,
当 时,则 为偶函数,满足题意;
当 时,则 为奇函数,不满足题意;
综上所述:实数 的值为 .
(2)函数 ,则函数 在定义域 内单调递减,
由 可得: ,解得 ,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以实数 的取值范围为 .
1.(2024高三·全国·专题练习)若幂函数 的图象经过点 ,则 =( )
A. B.2 C.4 D.
【答案】C
【分析】利用已知条件求得幂函数解析式,然后代入求解即可.
【详解】设幂函数 ,因为 的图象经过点 ,所以 ,解得 ,
所以 ,所以 .
故选:C
2.(23-24高一下·山西临汾·阶段练习)下列函数中,既是奇函数,又是在区间 上单调递减的函数
为( )
A. B.
C. D.
【答案】B
【分析】
根据基本初等函数的奇偶性和单调性进行判断即可.
【详解】对于A, 为偶函数,不符合题意;
对于B, 为奇函数,且在区间 上单调递减,符合题意;
对于C, 为偶函数,不符合题意;
对于D, 为奇函数,且在区间 上单调递增,不符合题意.
故选:B.
3.(23-24高一上·广东茂名·期末)已知幂函数 ,则 ( )
A. B.1 C. D.2
【答案】A
【分析】根据函数为幂函数得到方程,求出 ,得到解析式,代入求值即可.
【详解】因为 是幂函数,所以 ,即 ,
所以 , .
故选:A.
学科网(北京)股份有限公司 学科网(北京)股份有限公司4.(22-23高一·全国·课堂例题)幂函数 在第一象限内的图象依次是如图中的
曲线( )
A. B.
C. D.
【答案】D
【分析】根据幂函数的指数的大小与曲线的位置关系(可在直线 右侧)比较从而得出结论.
【详解】在第一象限内直线 的右侧,幂函数 的图象从上到下相应的指数 由大变小,即“指大
图高”,
所以幂函数 在第一象限内的图象为 在第一象限内的图象为 ,
在第一象限内的图象为 在第一象限内的图象为 .
故选:D
5.(23-24高一上·上海·阶段练习)已知幂函数 的图象不经过坐标原点,则
( )
A. B.3 C.1或 D. 或3
【答案】A
【分析】令系数等于1,得到 或 ,排除不合要求的解,得到答案.
【详解】令 ,解得 或 ,
当 时, ,图象经过坐标原点,不合要求,
当 时, ,图象不经过坐标原点,满足要求.
故选:A
6.(23-24高一下·上海·期中)已知实数 ,若函数 满足:当
时, 恒成立,则 可取值的个数为( )
A.4 B.3 C.2 D.1
【答案】C
【分析】把 的取值逐个代入检验可得答案.
学科网(北京)股份有限公司 学科网(北京)股份有限公司【详解】当 时,若 恒成立,则 ,即 ,
由于 ,所以 恒成立,此时符合题意;
当 时,若 恒成立,则 ,即 ,
由于 ,所以 恒成立,此时符合题意;
当 时,若 恒成立,则 ,即 ,
由于 ,所以 不成立,此时不符合题意;
当 时,若 ,则 ,不满足 ,不合题意.
故选:C
7.(2024·北京西城·一模)已知函数 ,若 存在最小值,则 的最大值为
( )
A. B. C. D.
【答案】A
【分析】运用二次函数的性质求得 的最小值,再结合幂函数的单调性,由题意列出不等式,求解
即可.
【详解】当 时, ,故当 时, 有最小值为 ;
时, 单调递减,所以 ,
由题意 存在最小值,则 ,解得 ,即 的最大值为 .
故选:A
8.(23-24高一上·四川成都·期中)已知函数 ,是 上的减函数,则a的取值范围
是( )
A. B. C. D.
【答案】C
【分析】根据函数的单调性列不等式,由此求得 的取值范围.
【详解】依题意, 在 上单调递减,
学科网(北京)股份有限公司 学科网(北京)股份有限公司所以 ,解得 ,
所以 的取值范围是
故选:C
二、多选题
9.(23-24高一下·四川眉山·开学考试)若幂函数 的图像经过 ,则下列说法正确的是
( )
A. B.
C. 的定义域是 D. 为偶函数
【答案】BC
【分析】先求出幂函数的解析式,再利用幂函数的性质即可判断.
【详解】由幂函数 ,
则 ,即 ,
且 ,解得 ,
,则A错误,B正确;
的定义域为 ,故C正确,D错误.
故选:BC.
三、填空题
10.(23-24高一上·安徽马鞍山·期中)已知幂函数 满足①函数图象不经过原点;②
,写出符合上述条件的一个函数解析式 .
【答案】 (答案不唯一)
【分析】本题根据幂函数的概念,结合题目给的限制性条件即可找到符合条件的函数.
【详解】因为 对 ,则 在 上为减函数,
又因为幂函数 ( 为常数),当 不经过原点时, 即可,
故可取 .
故答案为: (答案不唯一).
四、解答题
学科网(北京)股份有限公司 学科网(北京)股份有限公司11.(23-24高一上·山西忻州·期末)已知幂函数 .
(1)求 的解析式;
(2)判断函数 的奇偶性,并说明理由.
【答案】(1)
(2) 为奇函数,理由见解析
【分析】(1)根据幂函数的定义求出 可得答案;
(2) 为奇函数,利用奇函数的定义判断可得答案.
【详解】(1)依题意可得 ,
解得 ,所以 ;
(2) 为奇函数.
理由如下:
的定义域为 ,关于原点对称,
因为 ,
所以 为奇函数.
12.(23-24高一上·重庆九龙坡·期末)已知幂函数 的图象关于 轴对称.
(1)求 的值及函数 的解析式;
(2)设函数 ,求 在区间 上的值域.
【答案】(1) ,
(2)
【分析】(1)根据幂函数的定义及性质计算可得;
(2)首先得到 解析式,再结合二次函数的性质计算可得.
【详解】(1)因为 为幂函数,
所以 ,解得 或 ,
当 时, ,函数图象关于 轴对称,符合题意;
当 时, ,函数图象关于原点对称,不符合题意;
综上可得 , .
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2)因为 , ,
所以 ,
所以 在 上单调递减,在 上单调递增,
又 , , ,所以 ,
即 在区间 上的值域为 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司