文档内容
赤峰二中2024级高一上学期第一次月考
数学试卷
命题人 审核人 高一数学组
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.命题“∀x∈[−1,3],x2−3x+2<0”的否定为( )
A.∃x∈[−1,3],x2−3x+2≥0 B.∃x∈[−1,3],x2−3x+2>0
C.∀x∈[−1,3],x2−3x+2≥0 D.∃x∉[−1,3],x2−3x+2≥0
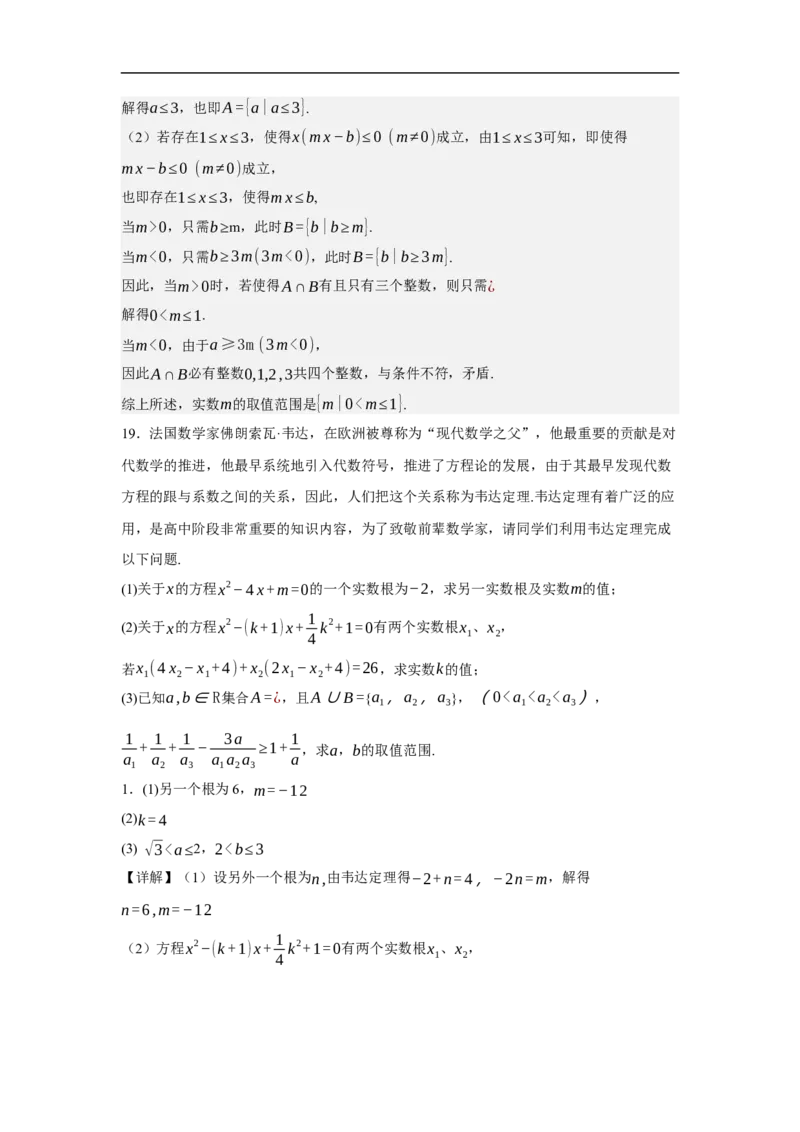
2.已知集合 ,集合 , ,则图中阴影部分表示的集合为
U=R A={x|−3b>0 ,当 m>0 时, >
b+m b
B. 集合 与集合 是相同的集合.
A={x∣y=x2+1} B={y∣y=x2+1}
m m
C. 若 b
a b
D. 所有的素数都是奇数
4. 设A=¿,B=¿,若A∩B=B,则实数a的值不可以为( )
1 1
A. B.3 C.0 D.
5 3
5.已知 11”是“ <1”的充要条件
x
B.命题“若 ,使得 ”的否定是“ ”
∃x ≥1 x2<2 ∀x<1,x2≥2
0 0
C.已知x,y∈R,则“|x|+|y|>0”是“x>0”的既不充分也不必要条件
a
D.已知a,b∈R,则“a−3b=0”是“ =3”的必要不充分条件
b
8.已知a,b是实数,则“a>1且b>1”是“ab+1>a+b”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 中国古代重要的数学著作《孙子算经》下卷有题: “今有物, 不知其数, 三三数之, 剩二; 五
五数之,剩三; 七七数之,剩二. 问: 物几何? ”现有数学语言表达如下: 已知
, ,若
A={x∣x=3n+2,n∈N∗} B={x∣x=5n+3,n∈N∗},C={x∣x=7n+2,n∈N∗}
x∈(A∩B∩C) ,则下列选项中符合题意的整数 x 为 ( )
A. 8 B. 23 C. 37 D. 128
10. 设 a,b∈A={x∣x=3m+1,m∈Z},c∈B={x∣x=3k−1,k∈Z}, 则( )
A.a+b∈A B.ab∈A
C.a+b∈B D.a+c∈B
11. 已知实数a,b,c满足a>b>c,且a+b+c=0,则下列结论中正确的是( )
A.a+b>0 B.ac D.(a−c)(b−c)< c2
a−b b−c 4
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知 在不等式 的解集中,则实数 的取值范围是
x=2 (k−1)x2−kx−4≥0 k
6
13. 已知 M={x∈N∣ ∈N} ,则集合 M 的子集的个数是
6−x
14.设集合M={1,2,3,4,5,6},选择M的两个非空子集A和B,要使B中最小的数大于A中最
大的数,满足这样条件的一个集合A与对应的一个集合B称为一组合,则不同的组合共有
种.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分 13 分)
设 R 为全集,集合 A={x∣a+1≤x≤2a+1},B={y∣y=4x−2,0≤x≤2} .
(1)若 ,求 ;
a=3 A∩B,(∁ A)∩B
R
(2)若 A⊆B ,求实数 a 的取值范围.
16. (本小题满分 15 分)
(1)已知集合 A={x∣a−1≤x≤a+1},B={x∣−1≤x≤3} ,若 “ x∈A ” 是 “ x∈B
” 的充分不必要条件,求实数 a 的取值范围.(2)命题 p:m∈R , m+1≤0 ,命题 q:∀x∈R,x2+mx+1≠0 ,若 p 与 q 不同时为真
命题, 求 m 的取值范围.
17. (本小题满分 17 分)(1)设a,b,c∈R证明:a2+b2+c2=ab+ac+bc的充要条件是a=b=c.
(2)已知a,b都是正实数,且a≠b,试比较a3+b3与ab2+a2b的大小,并证明.
18.已知命题p: 对于∀x∈R,x2+2ax+a2−a+3≥0为真命题.
(1)求实数a的取值的集合A;
(2)若∃x∈{x|1≤x≤3},使得x(mx−b)≤0 (m≠0)成立,记实数b的范围为集合B,
若A∩B中有且只有三个整数,求实数m的范围.
19. (本小题满分 17 分)法国数学家佛朗索瓦·韦达,在欧洲被尊称为“现代数学之父”,他
最重要的贡献是对代数学的推进,他最早系统地引入代数符号,推进了方程论的发展,由于其
最早发现代数方程的跟与系数之间的关系,因此,人们把这个关系称为韦达定理.韦达定理有
着广泛的应用,是高中阶段非常重要的知识内容,为了致敬前辈数学家,请同学们利用韦达定
理完成以下问题.
(1)关于x的方程x2−4x+m=0的一个实数根为−2,求另一实数根及实数m的值;
1
(2)关于x的方程x2−(k+1)x+ k2+1=0有两个实数根x 、x ,
4 1 2
若x (4x −x +4)+x (2x −x +4)=26,求实数k的值;
1 2 1 2 1 2
(3)已知a,b∈R集合A=¿,且A∪B={a ,a ,a },(00
C.∀x∈[−1,3],x2−3x+2≥0 D.∃x∉[−1,3],x2−3x+2≥0
2.已知集合 ,集合 , ,则图中阴影部分表示的集
U=R A={x|−3b>0 ,当 m>0 时, >
b+m b
B. 集合 与集合 是相同的集合.
A={x∣y=x2+1} B={y∣y=x2+1}
m m
C. 若 b
a b
D. 所有的素数都是奇数
4. 设A=¿,B=¿,若A∩B=B,则实数a的值不可以为( B )
1 1
A. B.3 C.0 D.
5 3
5.已知 11”是“ <1”的充要条件
x
B.命题“若 ,使得 ”的否定是“ ”
∃x ≥1 x2<2 ∀x<1,x2≥2
0 0
C.已知x,y∈R,则“|x|+|y|>0”是“x>0”的既不充分也不必要条件
a
D.已知a,b∈R,则“a−3b=0”是“ =3”的必要不充分条件
b
【答案】D
【难度】0.65
【知识点】判断命题的必要不充分条件、充要条件的证明、特称命题的否定及其真假判断、
既不充分也不必要条件【分析】利用充分不必要条件的定义判断A;利用存在量词命题的否定判断B;利用既不
充分也不必要定义判断C;利用必要不充分条件的定义判断D.
1 1 1
【详解】对于A,当 <1时,x<0或x>1,故x>1能推出 <1,但 <1不能推出x>1,
x x x
1
所以“x>1”是“ <1”的充分不必要条件,错误;
x
对于B,由存在量词命题的否定为全称量词命题知:
命题“若 ,使得 ”的否定是“ ”,错误;
∃x ≥1 x2<2 ∀x≥1,x2≥2
0 0
对于C,由|x|+|y|>0得x≠0或y≠0,故|x|+|y|>0推不出x>0,
但是当x>0时,|x|+|y|≥|x|+0=|x|>0一定成立,即x>0能推出|x|+|y|>0,
所以“|x|+|y|>0”是“x>0”的必要不充分条件,错误;
a
对于D,已知a,b∈R,当a=b=0时,满足a−3b=0,但是不满足 =3,
b
a
反之,当 =3时,则a=3b,即a−3b=0,
b
a
所以“a−3b=0”是“ =3”的必要不充分条件,正确.
b
故选:D
8.已知a,b是实数,则“a>1且b>1”是“ab+1>a+b”的( A )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【难度】0.85
【知识点】判断命题的充分不必要条件、作差法比较代数式的大小
【分析】根据充分必要条件的关系,结合不等式性质即可判断.
【详解】当a>1且b>1时, ab+1−(a+b)=(a−1)(b−1)>0,即a>1且b>1时ab+1>a+b
成立.
当ab+1>a+b时,即ab+1−(a+b)=(a−1)(b−1)>0解得a>1且b>1,或a<1且b<1
综上可知, “a>1且b>1”是“ab+1>a+b”的充分不必要条件
故选:A
【点睛】本题考查了不等式比较大小,充分必要条件的关系及判断,属于基础题.二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 中国古代重要的数学著作《孙子算经》下卷有题: “今有物, 不知其数, 三三数之, 剩二;
五五数之,剩三; 七七数之,剩二. 问: 物几何? ”现有数学语言表达如下: 已知
, ,
A={x∣x=3n+2,n∈N∗} B={x∣x=5n+3,n∈N∗},C={x∣x=7n+2,n∈N∗}
若 x∈(A∩B∩C) ,则下列选项中符合题意的整数 x 为 (BD)
A. 8 B. 23 C. 37 D. 128
9. 【 详 解 】 因 为 23=3×7+2=5×4+3=7×3+2 , 故
23∈(A∩B∩C);128=3×42+2=5× 25+3=7×18+2 ,故 128∈(A∩B∩C) ; 因
8=7×1+1 ,则 8∉C;37=3×12+1 ,则 37∉A
10. 设a,b∈A={x∣x=3m+1,m∈Z},c∈B={x∣x=3k−1,k∈Z},则( )
A.a+b∈A B.ab∈A
C.a+b∈B D.a+c∈B
【答案】BC
【分析】利用数的特征及元素与集合的关系计算即可.
【详解】设a=3u+1,b=3v+1,c=3w−1(u、v、w∈Z),
而a+b=3(u+v)+2=3(u+v+1)−1∈B,即A错误,C正确;
ab=9uv+3(u+v)+1=3(3uv+u+v)+1∈A,即B正确;
a+c=3u+1+3w−1=3(u+w)∉B,即D不正确.
故选:BC.
11. 已知实数a,b,c满足a>b>c,且a+b+c=0,则下列结论中正确的是( )
A.a+b>0 B.ac D.(a−c)(b−c)< c2
a−b b−c 4
【答案】ABD
【分析】根据不等式的基本性质和已知条件可逐项分析得到答案.
【详解】a+b+c=0且a>b>c,则a>0,c<0,则a+b>0,A正确;
因为a>b,c<0,所以acb>c,a−b>0,b−c>0,(a−b)−(b−c)=a+c−2b=−3b,
1 1
当b>0时,0 ;当b<0时,a−b>b−c>0,则
a−b b−c
1 1 1 1
< ,当b=0时,a−b=b−c,则 = ,故C错误;
a−b b−c a−b b−c
因为 (a−c)(b−c)− 9 c2=(a−c)(−a−2c)− 9 c2=−a2−ac− 1 c2=− ( a+ 1 c ) 2 ≤0 ,
4 4 4 2
1 1
当且仅当a=− c时,等号成立,此时由a+b+c=0可得b=− c,不符合a>b>c,
2 2
所以 − ( a+ 1 c ) 2 =0 不成立,故 − ( a+ 1 c ) 2 <0 ,即 (a−c)(b−c)< 9 c2 ,D正确.
2 2 4
故选:ABD
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知 在不等式 的解集中,则实数 的取值范围是__
x=2 (k−1)x2−kx−4≥0 k
12.k≥4 或 [4,+∞) 或 {k∣k≥4} ;
12.【详解】因为 x=2 在不等式的解集中,把 x=2 带入不等式得: 4(k−1)−2k−4≥0 ,
解得 k≥4
6
13. 已知 M={x∈N∣ ∈N} ,则集合 M 的子集的个数是_16__
6−x
6
13.【详解】解: 因为 ∈N ,所以 6−x=1,2,3,6 ,
6−x
又 x∈N ,所以 x=0,3,4,5 ,所以集合 M={0,3,4,5} ,所以集合 M 的子集个数为
24=16 个
14.设集合M={1,2,3,4,5,6},选择M的两个非空子集A和B,要使B中最小的数大于A中
最大的数,满足这样条件的一个集合A与对应的一个集合B称为一组合,则不同的组合共
有 种.【答案】129
【分析】讨论A中最大的数,分别求出A和B的非空子集,从而求得正确答案.
【详解】当A中最大的数为1时,B可以是{2,3,4,5,6}的非空子集,
有25−1=31(种)选择方法;
当A中最大的数为2时,A可以是{2}或{1,2},
B可以是 的非空子集,有 (种)选择方法;
{3,4,5,6} 2×(24−1)=30
当A中最大的数为3时,A可以是{3},{1,3},{2,3}或{1,2,3},
B可以是 的非空子集,有 (种)选择方法;
{4,5,6} 4×(23−1)=28
当A中最大的数为4时,A可以是{4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,3,4},
或 ,B可以是 的非空子集,有 (种)选择方法.
{1,2,3,4} {5,6} 8×(22−1)=24
当A中最大的数为5时,A可以是:{5},{1,5},{2,5},{3,5},{4,5},
{1,2,5},{1,3,5},{1,4,5},{2,3,5},{2,4,5},{1,2,3,5},{1,2,4,5},{1,3,4,5},{2,3,4,5},
{1,2,3,4,5},B是{6},有16×1=16(种)选择方法.
所以满足条件的集合共有31+30+28+24+16=129(种)不同的选择方法.
故答案为:129
【点睛】思路点睛:解题的突破口在于“B中最小的数大于A中最大的数”,解题的思想
方法是分类讨论的数学思想方法,根据集合A中最大的数进行分类讨论,分类讨论要做到
不重不漏.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分 13 分)
设 R 为全集,集合 A={x∣a+1≤x≤2a+1},B={y∣y=4x−2,0≤x≤2} .
(1)若 ,求 ;
a=3 A∩B,(∁ A)∩B
R
(2)若 A⊆B ,求实数 a 的取值范围.
16. (1) 由题意可得 B={y∣−2≤ y≤6} , ...2 分
当 a=3 时, A={x∣4≤x≤7} , ...3 分
所以 A∩B={x∣4≤x≤6} , .4分因为 C A={x∣x<4 ,或 x>7} , .5 分
R
所以 ....... 6 分
(C A)∩B={x∣−2≤x<4}
R
(2)由(1)知, B={y∣−2≤ y≤6} ,
若 A=⌀ ,即 a+1>2a+1 ,解得 a<0 ,此时满足 A⊆B ; ...8 分
{a+1≤2a+1
5
若 A≠⌀ ,要使 A⊆B ,则 a+1≥−2 ,解得 0≤a≤ , .12分
2
2a+1≤6
综上,若 ,所求实数 的取值范围为 { 5} .......... 13 分
A⊆B a a∣a≤
2
16. (本小题满分 15 分)
(1)已知集合 A={x∣a−1≤x≤a+1},B={x∣−1≤x≤3} ,若 “ x∈A ” 是 “
x∈B ” 的充分不必要条件,求实数 a 的取值范围.
(2)命题 p:m∈R , m+1≤0 ,命题 q:∀x∈R,x2+mx+1≠0 ,若 p 与 q 不同时为
真命题, 求 m 的取值范围.
16. (1) 由 x∈An 是 x∈Bn 的充分不必要条件,得 A 真包含于 B,….2 分
而 A=[a−1,a+1] ,显然 A≠B , ...3 分
{a−1≥−1
于是 ,解得 0≤a≤2 , ...6 分
a+1≤3
所以 a 的取值范围为 [0,2]…….7 分
(2)当命题 p 为真命题时, m≤−1,….8 分
当命题 q 为真命题时, Δ=m2−4<0 ,即 −20
∴a3+b3>ab2+a2b.
【点睛】此题考查利用作差法比较大小,关键在于对作差之后的代数式进行因式分解.
18.已知命题p: 对于∀x∈R,x2+2ax+a2−a+3≥0为真命题.
(1)求实数a的取值的集合A;
(2)若∃x∈{x|1≤x≤3},使得x(mx−b)≤0 (m≠0)成立,记实数b的范围为集合B,
若A∩B中有且只有三个整数,求实数m的范围.
【答案】(1) ;(2){ 1 }.
{a|a≤3} n| ≤n<1
2
【分析】(1)根据命题为真转化为不等式恒成立,利用判别式Δ<0求解;
(2)分类讨论n的正负求出集合B,再根据A∩B中只有一个整数建立不等式求解.
【详解】(1)由条件知,x2+2ax+a2−a+3≥0恒成立,
只需不等式所对应的二次方程x2+2ax+a2−a+3=0的Δ≤0.
∴Δ=4a2−4(a2−a+3)≤0解得a≤3,也即A={a|a≤3}.
(2)若存在1≤x≤3,使得x(mx−b)≤0 (m≠0)成立,由1≤x≤3可知,即使得
mx−b≤0 (m≠0)成立,
也即存在1≤x≤3,使得mx≤b,
当m>0,只需b≥m,此时B={b|b≥m}.
当m<0,只需b≥3m(3m<0),此时B={b|b≥3m}.
因此,当m>0时,若使得A∩B有且只有三个整数,则只需¿
解得0x2−2ax+b−2
恒成立,
所以方程 x2−2ax+b+1=0 有一个实根, 方程x2−2ax+b−2=0 有两个不等实数
根,可知A={a ,a } B={a }
1 3 2
所以a =a,(a>0),
2
又方程 有一个实根, ,可得
x2−2ax+b+1=0 ∆=4a2−4(b+1)=0 a2=b+1
方程x2−2ax+b−2=0 可化简为方程x2−2ax+a2−3=0 ,可知
,也可解得
a +a =2a>0,a a =a2−3>0 a =a−√3>0,a =a+√3>0
1 3 1 3 1 3
所以a>√3
由 1 1 1 3a 1 整理得a +a 1 3a 1
+ + − ≥1+ 1 3+ − ≥1+
a a a a a a a a a a a aa a
1 2 3 1 2 3 1 3 1 3
即a +a −3≥a a
1 3 1 3
整理得 0≤a≤2且a≠√3
又a>√3
综合上述可知 √3Δ
1 2
若" 可分为两种情况:
A∪B={a ,a ,a },
1 2 3
(1)A∩B=∅,此时A中一定有两个元素,B中有一个元素,即满足Δ =0⇒a2=b+1
2
把a2=b+1代入方程x2−2ax+b−2=0中,得到:x2−2ax+a2−3=0
解得: ,
x =√3+a x =a−√3
1 2
把a2=b+1代入方程x2−2ax+b+1=0中,得x2−2ax+a2=0,
解得x =a
3
显然, ,则
a−√30,a =a>0,a =a+√3>0⇒a>√3
1 2 3
1 1 1 3a 1
此时, + + − ≥1+
a a a a a a a
1 2 3 1 2 3
1 1 1
即: + − ≥1
a−√3 a+√3 (a−√3)(a+√3)
解得:0≤a<√3或√3√3,则√3