文档内容
格致课堂
6.4.2 向量在物理中的应用举例
一、选择题
1.一物体受到相互垂直的两个力 、 的作用,两力大小都为 ,则两个力的合力的大小为
A. B.0
C. D.
【答案】C
【解析】
根据向量加法的平行四边形法则,合力 的大小为 .
本题选择C选项.
2.已知两个力 的夹角为90°,它们的合力大小为10N,合力与 的夹角为60°,那么 的大小为(
)
A. N B.5N
C.10N D. N
【答案】A
【解析】
对应向量如图由于α=60°,则 的大小为
| | sin60°=10× = N.故选A。
3.用力F推动一物体水平运动s m,设F与水平面的夹角为 ,则对物体所做的功为( )格致课堂
A.|F|·s B.F·cos ·s C.F·sin ·s D.|F|·cos ·s
【答案】D
【解析】
W=|F|·cos ·s.故选D。
4.已知三个力 同时作用于某物体上一点,为使物体保持平衡,现
加上一个力 ,则 等于( )
A. B. C. D.
【答案】D
【解析】
为使物体平衡,即合外力为零,即4个向量相加等于零向量,
∴ .故选D。
5.(多选题)在水流速度 的自西向东的河中,如果要使船以 的速度从河的南岸垂直
到达北岸,则船出发时行驶速度的方向和大小为( )
A.北偏西 B.北偏西 ,
30km/h
C. D.
【答案】AC
【解析】
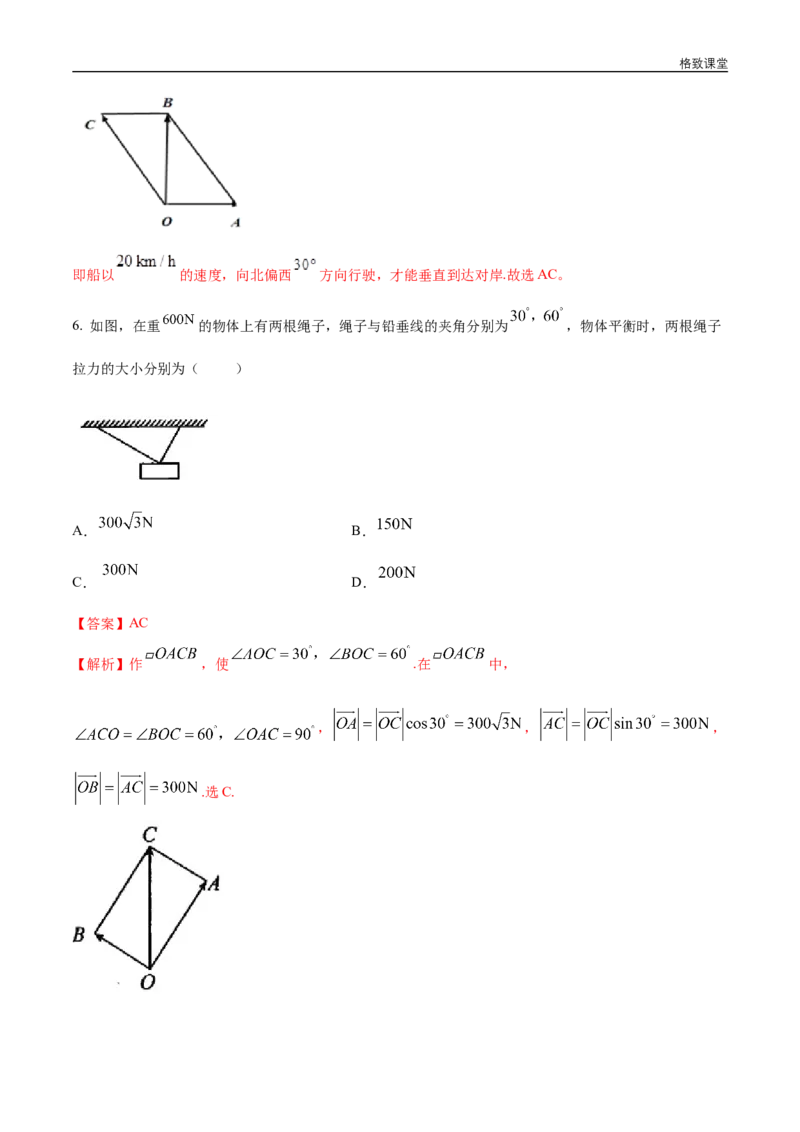
如图,船从O点出发,沿OC方向行驶,才能垂直到达河的对岸, 则
,
所以 ,格致课堂
即船以 的速度,向北偏西 方向行驶,才能垂直到达对岸.故选AC。
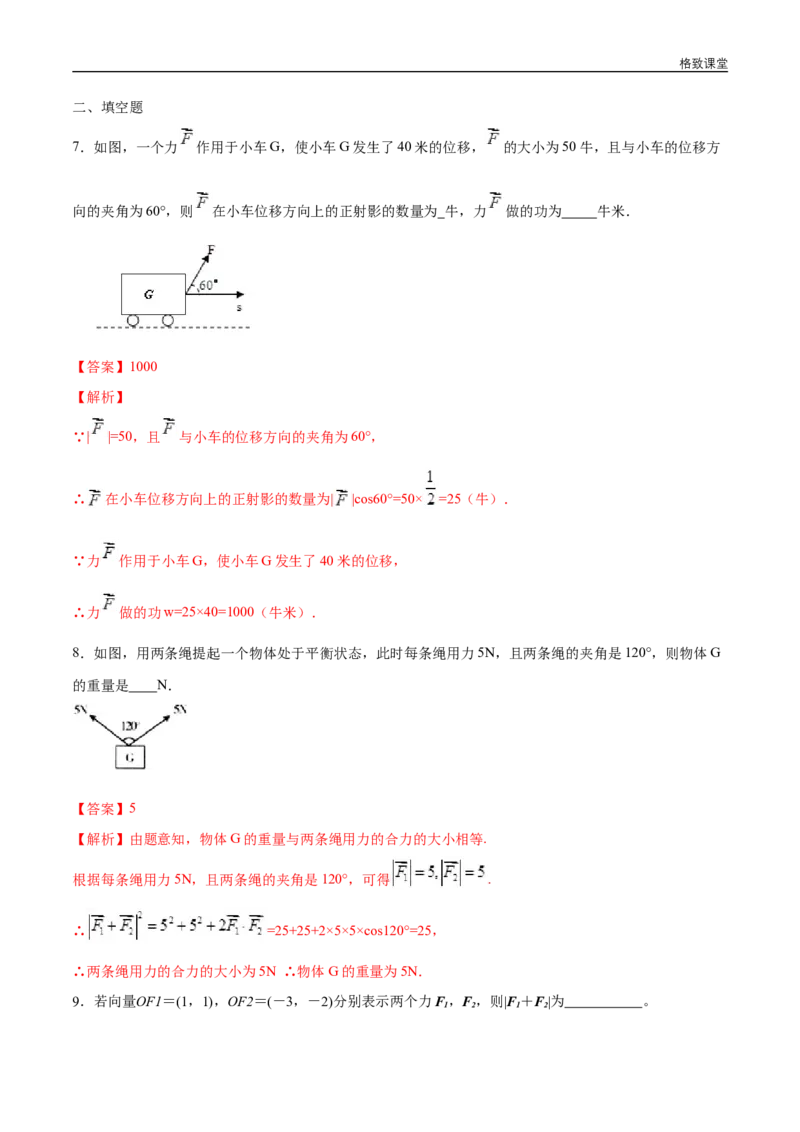
6. 如图,在重 的物体上有两根绳子,绳子与铅垂线的夹角分别为 ,物体平衡时,两根绳子
拉力的大小分别为( )
A. B.
C. D.
【答案】AC
【解析】作 ,使 .在 中,
, , ,
.选C.格致课堂
二、填空题
7.如图,一个力 作用于小车G,使小车G发生了40米的位移, 的大小为50牛,且与小车的位移方
向的夹角为60°,则 在小车位移方向上的正射影的数量为 牛,力 做的功为 牛米.
【答案】1000
【解析】
∵| |=50,且 与小车的位移方向的夹角为60°,
∴ 在小车位移方向上的正射影的数量为| |cos60°=50× =25(牛).
∵力 作用于小车G,使小车G发生了40米的位移,
∴力 做的功w=25×40=1000(牛米).
8.如图,用两条绳提起一个物体处于平衡状态,此时每条绳用力5N,且两条绳的夹角是120°,则物体G
的重量是 N.
【答案】5
【解析】由题意知,物体G的重量与两条绳用力的合力的大小相等.
根据每条绳用力5N,且两条绳的夹角是120°,可得 .
∴ =25+25+2×5×5×cos120°=25,
∴两条绳用力的合力的大小为5N ∴物体G的重量为5N.
9.若向量OF1=(1,1),OF2=(-3,-2)分别表示两个力F ,F ,则|F +F |为 。
1 2 1 2格致课堂
A. B.2 C. D.
【答案】
【解析】 由于F +F =(1,1)+(-3,-2)=(-2,-1),
1 2
所以|F +F |==,
1 2
故选C.
⃗AB
10.已知 =(2,3)作用一物体,使物体从A(2,0)移动到B(4,0),则 = ,力 对
物体作的功为 .
【答案】 (2,3) 4
【解析】根据题意,力 对物体作的功为W= =(2,3) =2×2+3×0=4.
三、解答题
11.已知两恒力F=(3,4),F=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
1 2
(1)求F,F 分别对质点所做的功;
1 2
(2)求F,F 的合力F对质点所做的功.
1 2
【答案】(1)-99 J,-3 J(2)-102 J
【解析】
(1) =(7,0)-(20,15)=(-13,-15),W=F· =(3,4)·(-13,-15)
1 1
=3×(-13)+4×(-15)=-99(J),W=F· =(6,-5)·(-13,-15)
2 2
=6×(-13)+(-5)×(-15)=-3(J).
∴力F,F 对质点所做的功分别为-99 J和-3 J.
1 2
(2)W=F· =(F+F)· =[(3,4)+(6,-5)]·(-13,-15)
1 2
=(9,-1)·(-13,-15)=9×(-13)+(-1)×(-15)=-117+15=-102(J).
∴合力F对质点所做的功为-102 J.
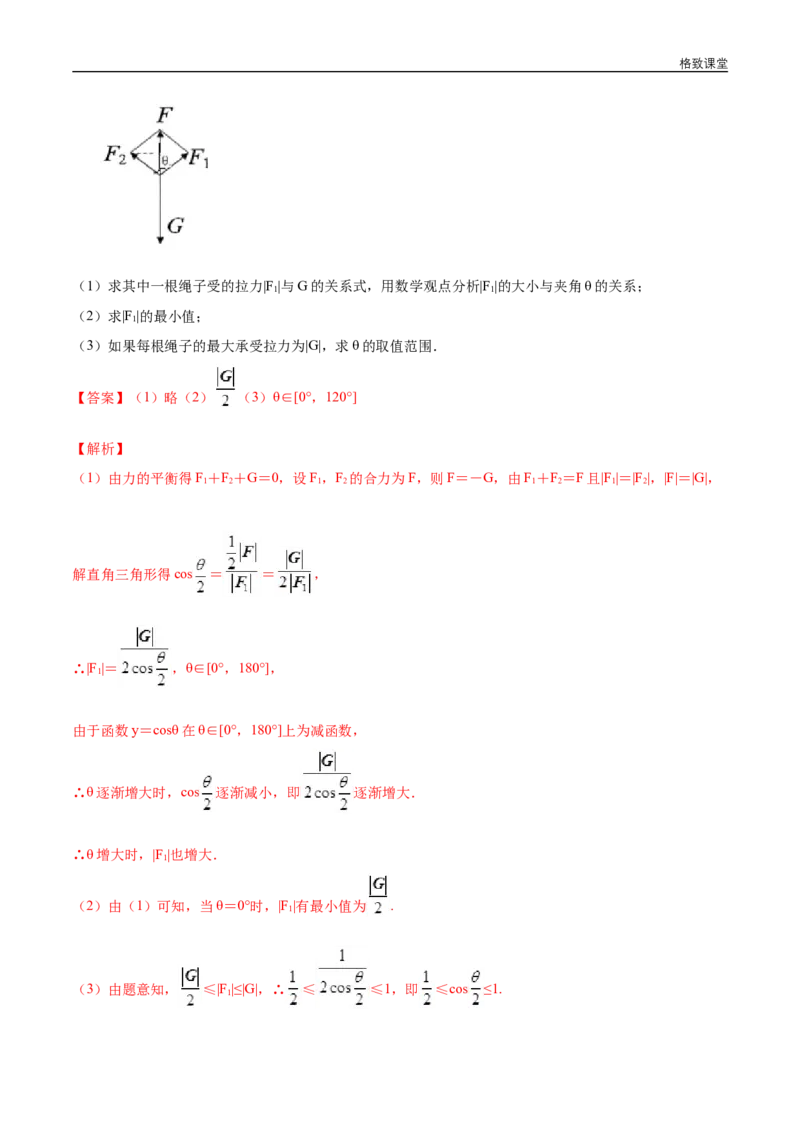
12.如图,用两条同样长的绳子拉一物体,物体受到的重力为G,两绳受到的拉力分别为F、F,夹角为
1 2
θ.格致课堂
(1)求其中一根绳子受的拉力|F|与G的关系式,用数学观点分析|F|的大小与夹角θ的关系;
1 1
(2)求|F|的最小值;
1
(3)如果每根绳子的最大承受拉力为|G|,求θ的取值范围.
【答案】(1)略(2) (3)θ∈[0°,120°]
【解析】
(1)由力的平衡得F+F+G=0,设F,F 的合力为F,则F=-G,由F+F=F且|F|=|F|,|F|=|G|,
1 2 1 2 1 2 1 2
解直角三角形得cos = = ,
∴|F|= ,θ∈[0°,180°],
1
由于函数y=cosθ在θ∈[0°,180°]上为减函数,
∴θ逐渐增大时,cos 逐渐减小,即 逐渐增大.
∴θ增大时,|F|也增大.
1
(2)由(1)可知,当θ=0°时,|F|有最小值为 .
1
(3)由题意知, ≤|F|≤|G|,∴ ≤ ≤1,即 ≤cos ≤1.
1格致课堂
由于y=cosθ在[0°,180°]上为减函数,
∴0°≤ ≤60°,∴θ∈[0°,120°].