文档内容
格致课堂
8.1 基本几何图形
第1课时 棱柱、棱锥、棱台
(用时45分钟)
【选题明细表】
知识点、方法 题号
棱柱、棱锥、棱台的结构特点 1,2,3,4,6,7
空间几何体的判断 8,11,12
多面体的展开图问题 5,9,10
基础巩固
1.下面的几何体中是棱柱的有( )
A.3个 B.4个 C.5个 D.6个
【答案】C
【解析】选C 棱柱有三个特征:(1)有两个面相互平行;(2)其余各面是四边形;(3)侧棱相互平行.本题所
给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤符合,故选C.
2.下列图形中,是棱台的是( )
【答案】C
【解析】选C 由棱台的定义知,A、D的侧棱延长线不交于一点,所以不是棱台;B中两个面不平行,不
是棱台,只有C符合棱台的定义,故选C.
3.一个棱锥的各棱长都相等,那么这个棱锥一定不是( )
A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥格致课堂
【答案】D
【解析】选D 由题意可知,每个侧面均为等边三角形,每个侧面的顶角均为60°,如果是六棱锥,因为
6×60°=360°,所以顶点会在底面上,因此不是六棱锥.
4.关于空间几何体的结构特征,下列说法不正确的是( )
A.棱柱的侧棱长都相等
B.四棱锥有五个顶点
C.三棱台的上、下底面是相似三角形
D.有的棱台的侧棱长都相等
【答案】B
【解析】选B 根据棱锥顶点的定义可知,四棱锥仅有一个顶点.故选B.
5.下列图形中,不能折成三棱柱的是( )
【答案】C
【解析】选C C中,两个底面均在上面,因此不能折成三棱柱,其余均能折为三棱柱.
6.四棱柱有________条侧棱,________个顶点.
【答案】4 8
【解析】四棱柱有4条侧棱,8个顶点(可以结合正方体观察求得).
7.一棱柱有10个顶点,其所有的侧棱长的和为60 cm,则每条侧棱长为________ cm.
【答案】12
【解析】该棱柱为五棱柱,共有5条侧棱,每条侧棱长都相等,∴每条侧棱长为12 cm.
8.根据下列关于空间几何体的描述,说出几何体的名称:
(1)由6个平行四边形围成的几何体;
(2)由7个面围成的几何体,其中一个面是六边形,其余6个面都是有一个公共顶点的三角形;
(3)由5个面围成的几何体,其中上、下两个面是相似三角形,其余3个面都是梯形,并且这些梯形的
腰延长后能相交于一点.
【答案】(1)四棱柱.(2)六棱锥.(3)三棱台.
【解析】 (1)这是一个上、下底面是平行四边形,4个侧面也是平行四边形的四棱柱.
(2) 这是一个六棱锥.
(3) 这是一个三棱台.格致课堂
能力提升
9.下列图形经过折叠可以围成一个棱柱的是( )
【答案】D
【解析】选D A、B、C中底面图形的边数与侧面的个数不一致,故不能围成棱柱.故选D.
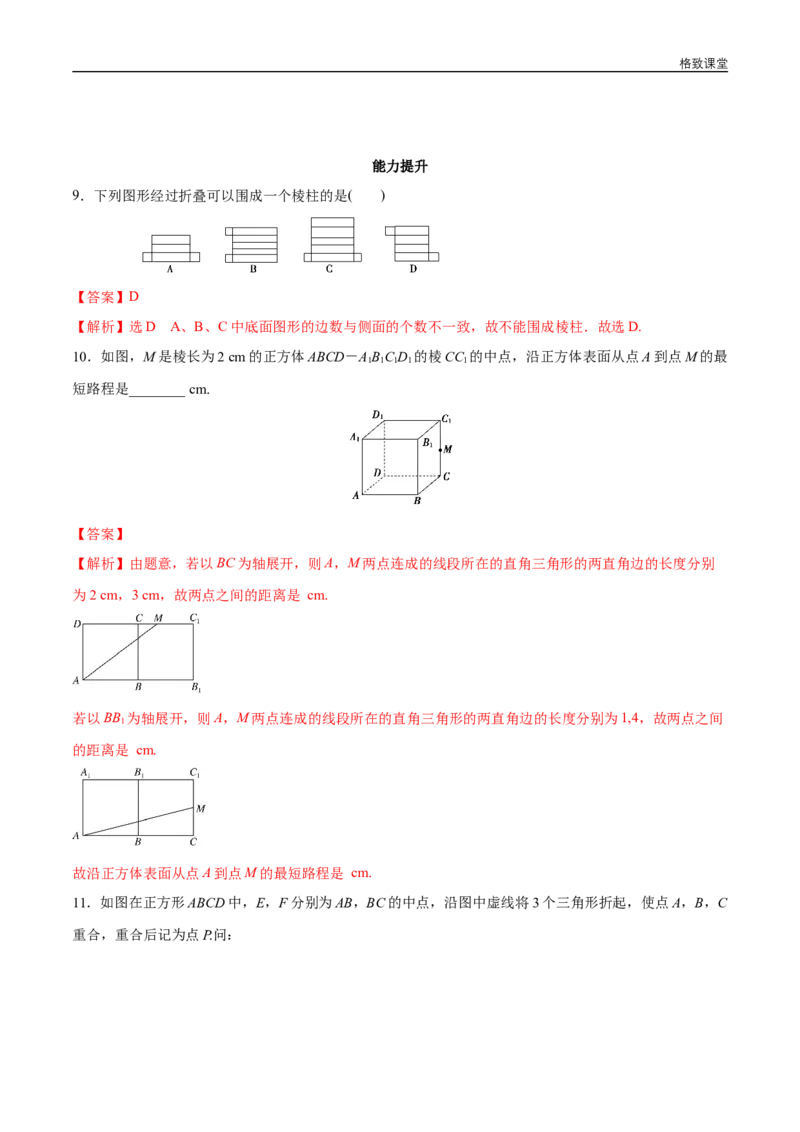
10.如图,M是棱长为2 cm的正方体ABCD-ABC D 的棱CC 的中点,沿正方体表面从点A到点M的最
1 1 1 1 1
短路程是________ cm.
【答案】
【解析】由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别
为2 cm,3 cm,故两点之间的距离是 cm.
若以BB 为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间
1
的距离是 cm.
故沿正方体表面从点A到点M的最短路程是 cm.
11.如图在正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C
重合,重合后记为点P.问:格致课堂
(1)折起后形成的几何体是什么几何体?
(2)若正方形边长为2a,则每个面的三角形面积为多少?
【答案】(1)三棱锥.(2)S =a2,S =S =×2a×a=a2,S =a2.
PEF DPF DPE DEF
△ △ △ △
【解析】(1)如图折起后的几何体是三棱锥.
(2)S =a2,S =S =×2a×a=a2,S =a2.
PEF DPF DPE DEF
△ △ △ △
素养达成
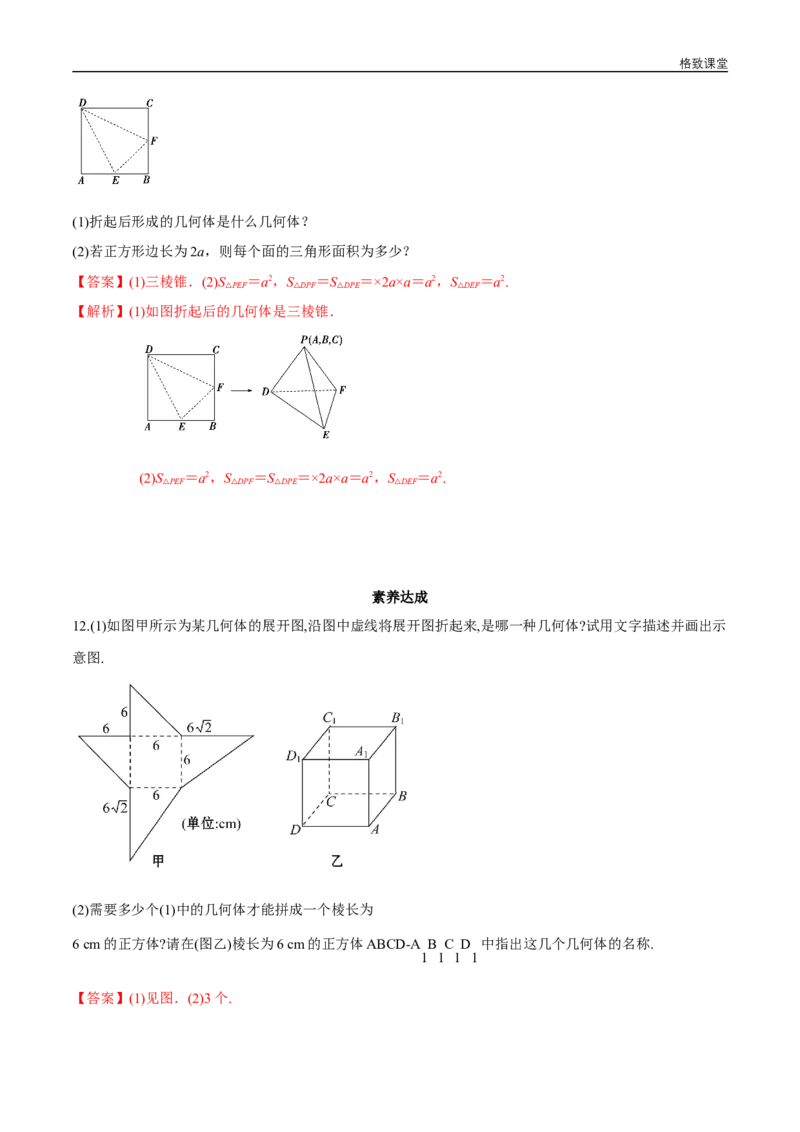
12.(1)如图甲所示为某几何体的展开图,沿图中虚线将展开图折起来,是哪一种几何体?试用文字描述并画出示
意图.
(2)需要多少个(1)中的几何体才能拼成一个棱长为
6 cm的正方体?请在(图乙)棱长为6 cm的正方体ABCD-A B C D 中指出这几个几何体的名称.
1 1 1 1
【答案】(1)见图.(2)3个.格致课堂
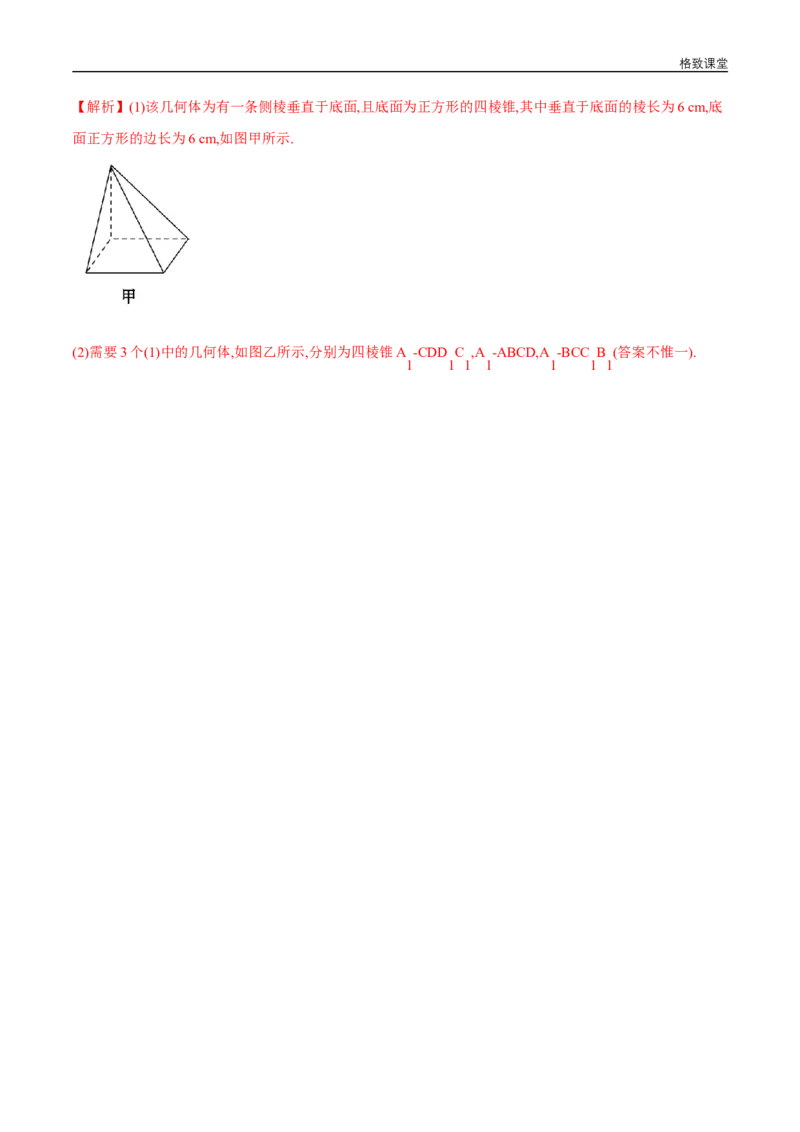
【解析】(1)该几何体为有一条侧棱垂直于底面,且底面为正方形的四棱锥,其中垂直于底面的棱长为6 cm,底
面正方形的边长为6 cm,如图甲所示.
(2)需要3个(1)中的几何体,如图乙所示,分别为四棱锥A -CDD C ,A -ABCD,A -BCC B (答案不惟一).
1 1 1 1 1 1 1