文档内容
格致课堂
8.1 基本几何图形
第 2 课时 圆柱、圆锥、圆台、球、简单组合体
(用时45分钟)
【选题明细表】
知识点、方法 题号
旋转体的结构特点 1,2,6,9
空间几何体 3,4,8
旋转体的有关计算 5,7,10,11,12
基础巩固
1.如图所示的图形中有( )
A.圆柱、圆锥、圆台和球 B.圆柱、球和圆锥
C.球、圆柱和圆台 D.棱柱、棱锥、圆锥和球
【答案】B
【解析】选B 根据题中图形可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆台,故应选B.
2.下列命题中正确的是( )
A.将正方形旋转不可能形成圆柱
B.以直角梯形的一腰为轴旋转所得的旋转体是圆台
C.圆柱、圆锥、圆台的底面都是圆面
D.通过圆台侧面上一点,有无数条母线
【答案】C
【解析】选C 将正方形绕其一边所在直线旋转可以形成圆柱,所以A错误;B中必须以垂直于底
边的腰为轴旋转才能得到圆台,所以B错误;通过圆台侧面上一点,只有一条母线,所以D错误,
故选C.
3.一个直角三角形绕斜边旋转360°形成的空间几何体是( )格致课堂
A.一个圆锥 B.一个圆锥和一个圆柱
C.两个圆锥 D.一个圆锥和一个圆台
【答案】C
【解析】选C 将直角三角形绕斜边旋转360°,相当于两个三角形以直角边旋转两360°,故两个圆
锥.
4.如图所示的几何体,关于其结构特征,下列说法不正确的是( )
A.该几何体是由2个同底的四棱锥组成的几何体
B.该几何体有12条棱、6个顶点
C.该几何体有8个面,并且各面均为三角形
D.该几何体有9个面,其中一个面是四边形,其余各面均为三角形
【答案】D
【解析】选D 该几何体用平面ABCD可分割成两个四棱锥,因此它是这两个四棱锥的组合体,因
而四边形ABCD是它的一个截面而不是一个面.故D说法不正确.
5.用一张长为8,宽为4的矩形硬纸卷成圆柱的侧面,则相应圆柱的底面半径是( )
A.2 B.2π
C.或 D.或
【答案】C
【解析】选C 如图所示,设底面半径为r,若矩形的长8恰好为卷成圆柱底面的周长,则2πr=
8,所以r=;同理,若矩形的宽4恰好为卷成圆柱的底面周长,则2πr=4,所以r=.所以选C.
6.如图,在△ABC中,∠ABC=120°,它绕AB边所在直线旋转一周后形成的几何体结构是
________________________.格致课堂
【答案】大圆锥挖去了一个同底面的小圆锥
【解析】旋转后的几何体结构如下:是一个大圆锥挖去了一个同底面的小圆锥.
7.一个圆锥截成圆台,已知圆台的上下底面半径的比是1∶4,截去小圆锥的母线长为3 cm,则圆
台的母线长为________ cm.
【答案】9
【解析】如图所示,设圆台的母线长为x cm,
截得的圆台的上、下底半径分别为r cm,4r cm,
根据三角形相似的性质,得=,解得x=9(cm).
8.指出图中的三个几何体分别是由哪些简单几何体组成的.
【答案】(1)一个圆锥、一个圆柱和一个圆台拼接而成.
(2)一个六棱柱和一个圆柱拼接而成.
(3)几何体由一个球和一个圆柱中挖去一个以圆柱下底面为底面、上底面圆心为顶点的圆锥拼接
而成.
【解析】(1)几何体由一个圆锥、一个圆柱和一个圆台拼接而成.
(2)几何体由一个六棱柱和一个圆柱拼接而成.
(3)几何体由一个球和一个圆柱中挖去一个以圆柱下底面为底面、上底面圆心为顶点的圆锥拼接
而成.
能力提升
9.如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面、下底面圆心为顶点的圆锥而得
到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )格致课堂
A.①② B.①③
C.①④ D.①⑤
【答案】D
【解析】选D 一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是
矩形除去一条边,圆锥的轮廓是三角形除去一条边或抛物线的一部分,故选D.
10.在半径为13的球面上有A、B、C三点,其中AC=6,BC=8,AB=10,则球心到经过这三个
点的截面的距离为________.
【答案】12
【解析】由线段的长度知△ABC是以AB为斜边的直角三角形,所以其外接圆的半径r==5,所以
d==12.
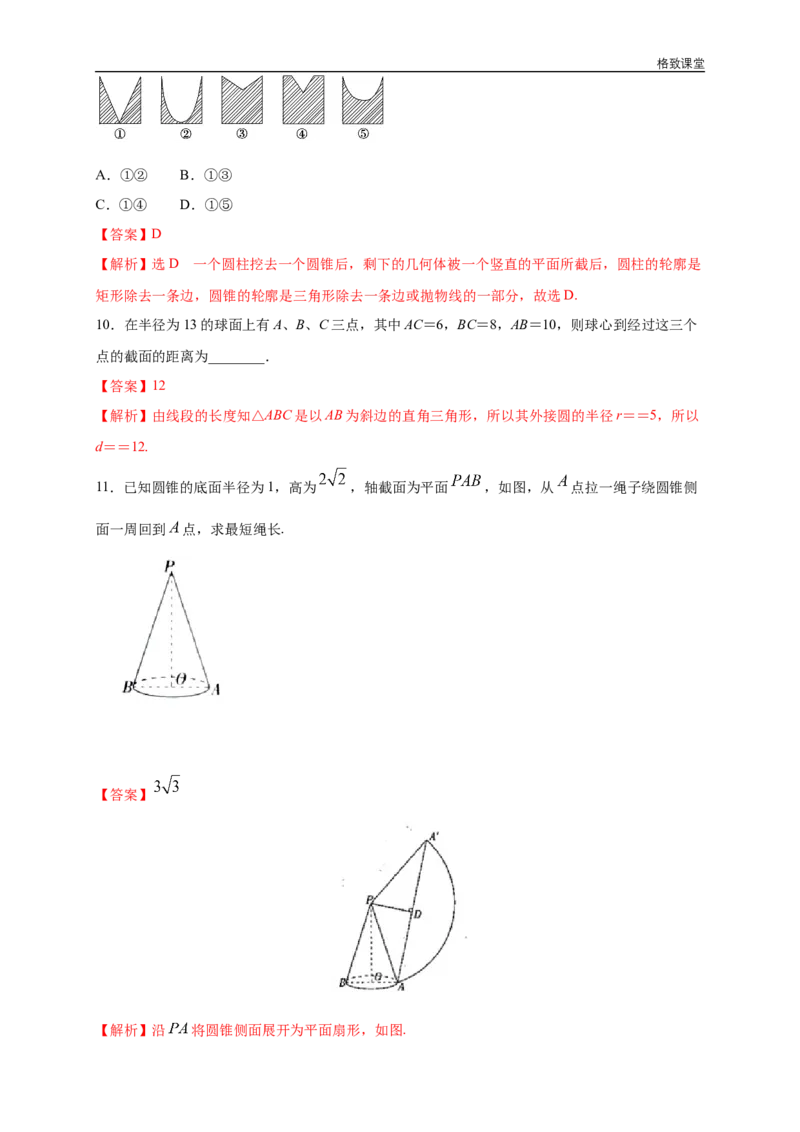
11.已知圆锥的底面半径为1,高为 ,轴截面为平面 ,如图,从 点拉一绳子绕圆锥侧
面一周回到 点,求最短绳长.
【答案】
【解析】沿 将圆锥侧面展开为平面扇形,如图.格致课堂
, , , .
作 交 于点D,则 .
,
∴最短绳长为 .
素养达成
12.圆台的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面的半径的2倍,求
两底面的半径及两底面面积之和.
【答案】圆台上底面半径为a,下底面半径为2a,两底面面积之和为5πa2.
【解析】设圆台上底面半径为r,则下底面半径为2r.将圆台还原为圆锥,如图,则有∠ABO=30°.
在Rt△BO′A′中,=sin 30°,
∴BA′=2r.
在Rt△BOA中,=sin 30°,
∴BA=4r.
又BA-BA′=AA′,即4r-2r=2a,∴r=a.
∴S=πr2+π(2r)2=5πr2=5πa2.∴圆台上底面半径为a,下底面半径为2a,两底面面积之和为5πa2.