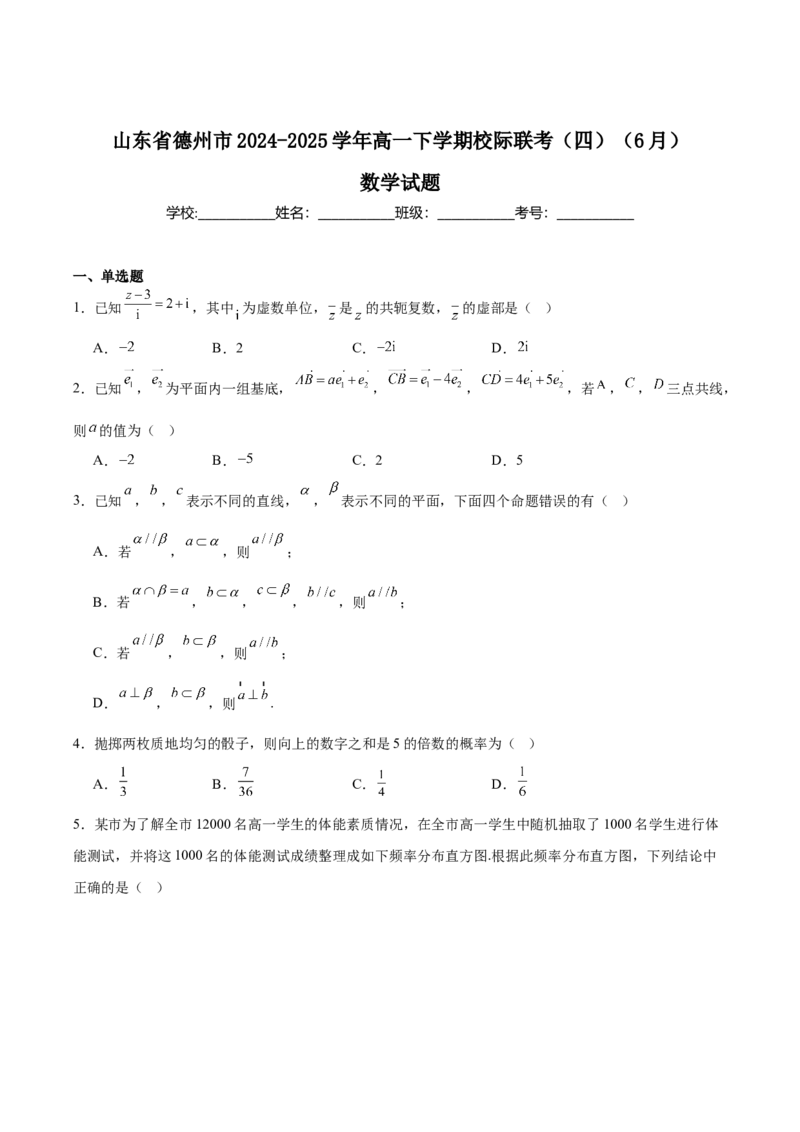文档内容
山东省德州市2024-2025学年高一下学期校际联考(四)(6月)
数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知 ,其中 为虚数单位, 是 的共轭复数, 的虚部是( )
A. B.2 C. D.
2.已知 , 为平面内一组基底, , , ,若 , , 三点共线,
则 的值为( )
A. B. C.2 D.5
3.已知 , , 表示不同的直线, , 表示不同的平面,下面四个命题错误的有( )
A.若 , ,则 ;
B.若 , , , ,则 ;
C.若 , ,则 ;
D. , ,则 .
4.抛掷两枚质地均匀的骰子,则向上的数字之和是5的倍数的概率为( )
A. B. C. D.
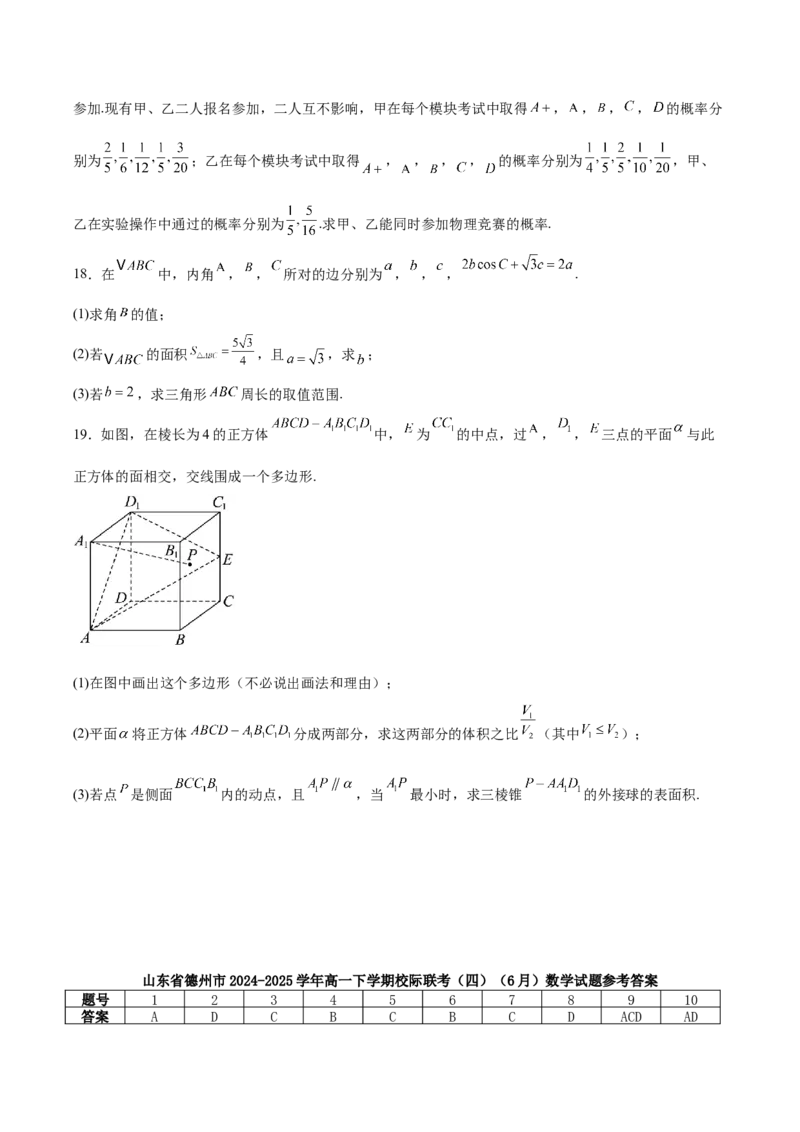
5.某市为了解全市12000名高一学生的体能素质情况,在全市高一学生中随机抽取了1000名学生进行体
能测试,并将这1000名的体能测试成绩整理成如下频率分布直方图.根据此频率分布直方图,下列结论中
正确的是( )A.图中 一组的频率为0.015
B.估计样本数据的众数
C.估计样本数据的 分位数为88.75
D.由样本数据可估计全市高一学生体测成绩优异(80分及以上)的人数约为7000人
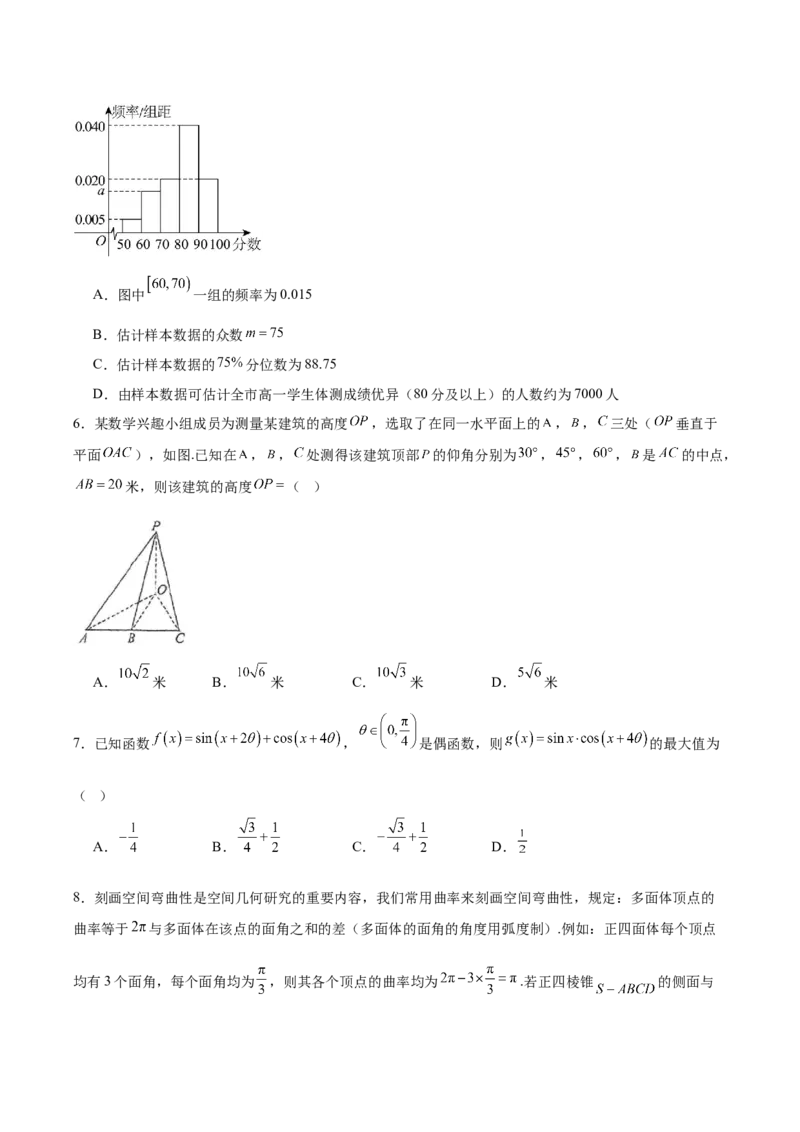
6.某数学兴趣小组成员为测量某建筑的高度 ,选取了在同一水平面上的 , , 三处( 垂直于
平面 ),如图.已知在 , , 处测得该建筑顶部 的仰角分别为 , , , 是 的中点,
米,则该建筑的高度 ( )
A. 米 B. 米 C. 米 D. 米
7.已知函数 , 是偶函数,则 的最大值为
( )
A. B. C. D.
8.刻画空间弯曲性是空间几何研究的重要内容,我们常用曲率来刻画空间弯曲性,规定:多面体顶点的
曲率等于 与多面体在该点的面角之和的差(多面体的面角的角度用弧度制).例如:正四面体每个顶点
均有3个面角,每个面角均为 ,则其各个顶点的曲率均为 .若正四棱锥 的侧面与底面的夹角的正切值为 ,则四棱锥 在顶点 处的曲率为( )
A. B. C. D.
二、多选题
9.若复数 ,则( )
A. B. 在复平面内对应的点位于第一象限
C. D.复数 满足 ,则 的最小值为
10.为加强青少年科学健身普及和健康干预,让年轻一代在运动中强意志、健身心,某校举办一场篮球赛,
其中每队上场5人,每人得分情况如下表(单位:分),则下列结论正确的是( )
甲队 乙队
5 10 23 12 8 8 8 15 7 6
A.运动员得分极差甲队大于乙队 B.运动员得分均值甲队小于乙队
C.甲队运动员得分的75%分位数为8 D.相较于甲队,乙队运动员实力更均衡
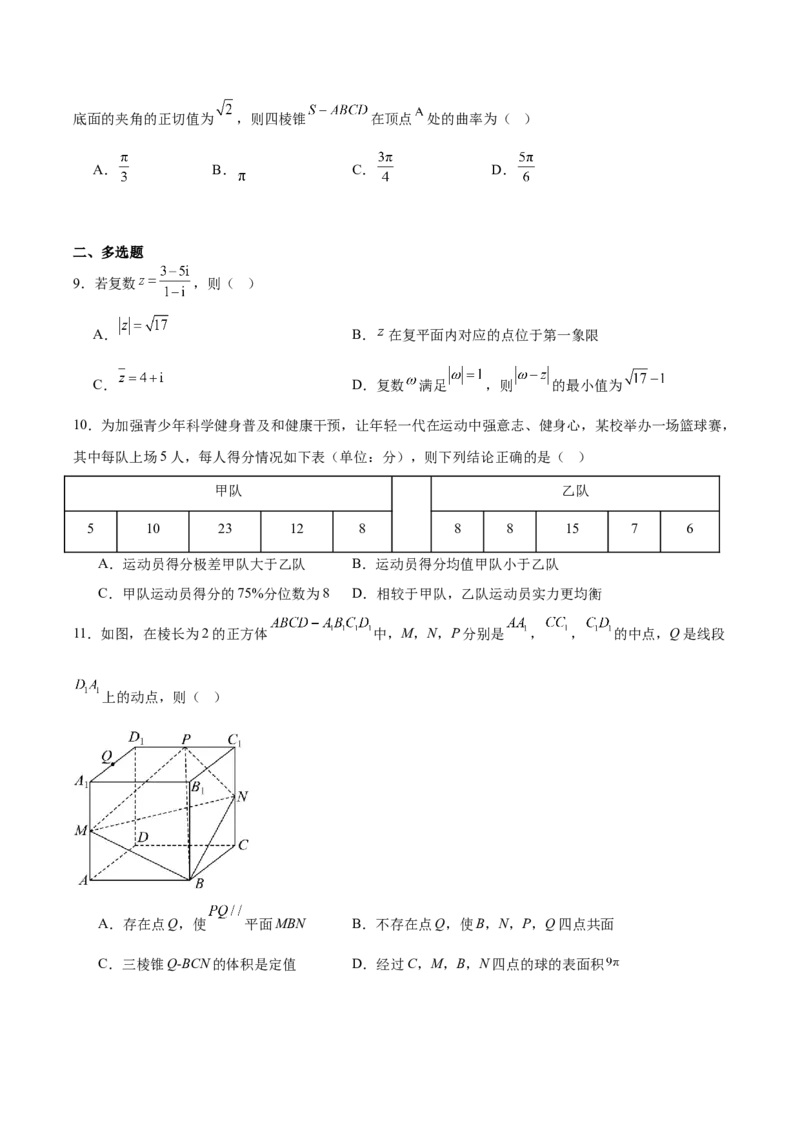
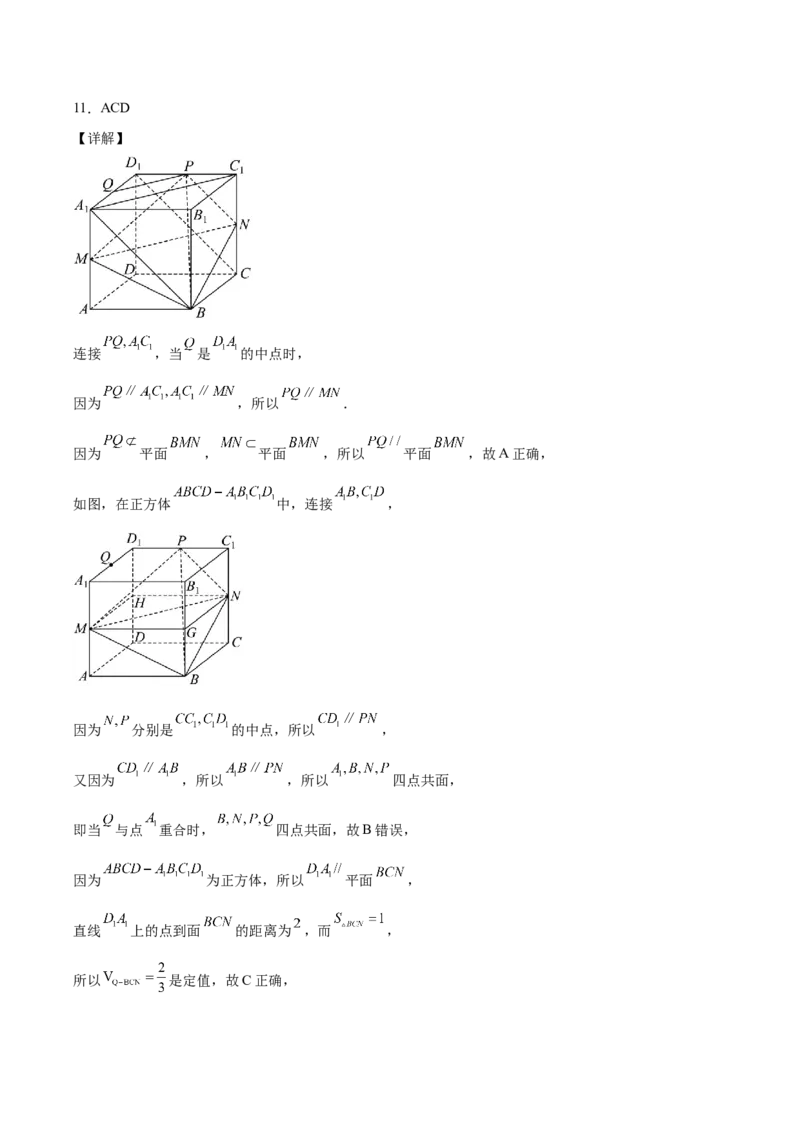
11.如图,在棱长为2的正方体 中,M,N,P分别是 , , 的中点,Q是线段
上的动点,则( )
A.存在点Q,使 平面MBN B.不存在点Q,使B,N,P,Q四点共面
C.三棱锥Q-BCN的体积是定值 D.经过C,M,B,N四点的球的表面积三、填空题
12.哪吒系列手办盲盒包含哪吒、敖丙、哪吒父母共4个人物手办,小明随机购买2个盲盒(2个盲盒内
人物一定不同),则恰有哪吒及其父母中的一位的概率为 .
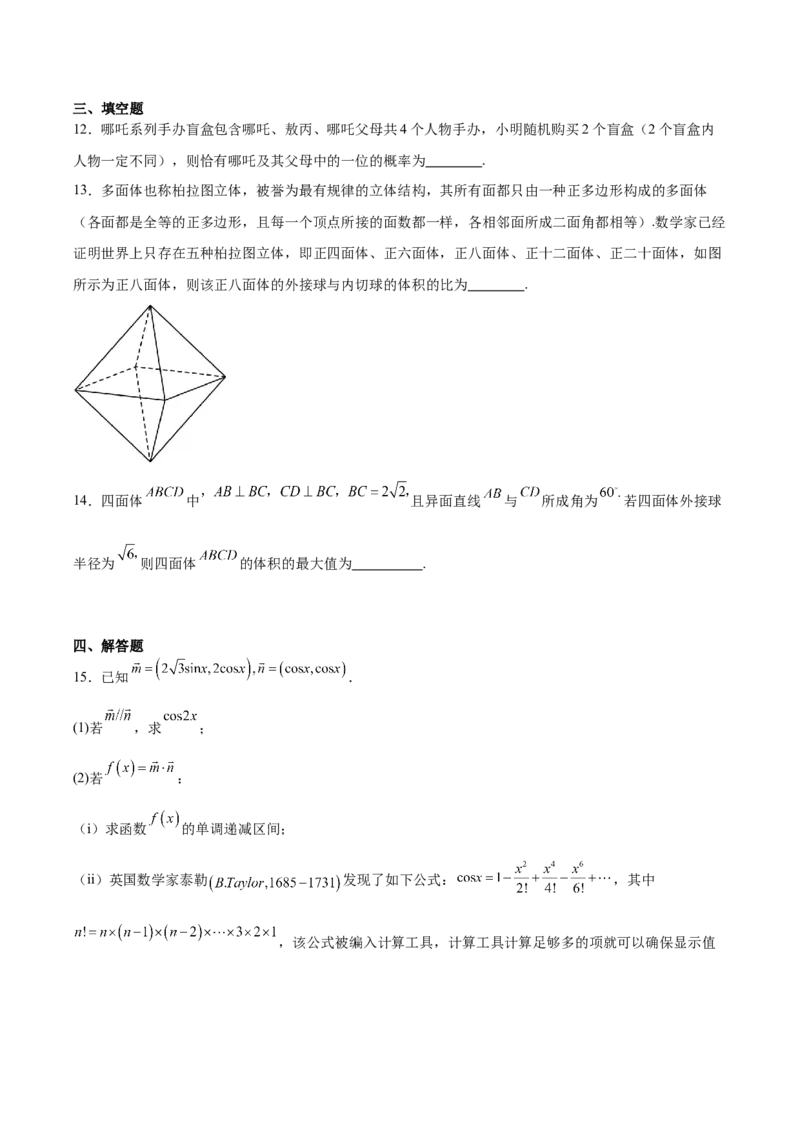
13.多面体也称柏拉图立体,被誉为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体
(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经
证明世界上只存在五种柏拉图立体,即正四面体、正六面体,正八面体、正十二面体、正二十面体,如图
所示为正八面体,则该正八面体的外接球与内切球的体积的比为 .
14.四面体 中 且异面直线 与 所成角为 若四面体外接球
半径为 则四面体 的体积的最大值为 .
四、解答题
15.已知 .
(1)若 ,求 ;
(2)若 :
(i)求函数 的单调递减区间;
(ii)英国数学家泰勒 发现了如下公式: ,其中
,该公式被编入计算工具,计算工具计算足够多的项就可以确保显示值的准确性.运用上述思想,计算 的值.(结果精确到小数点后3位,参考数据:
)
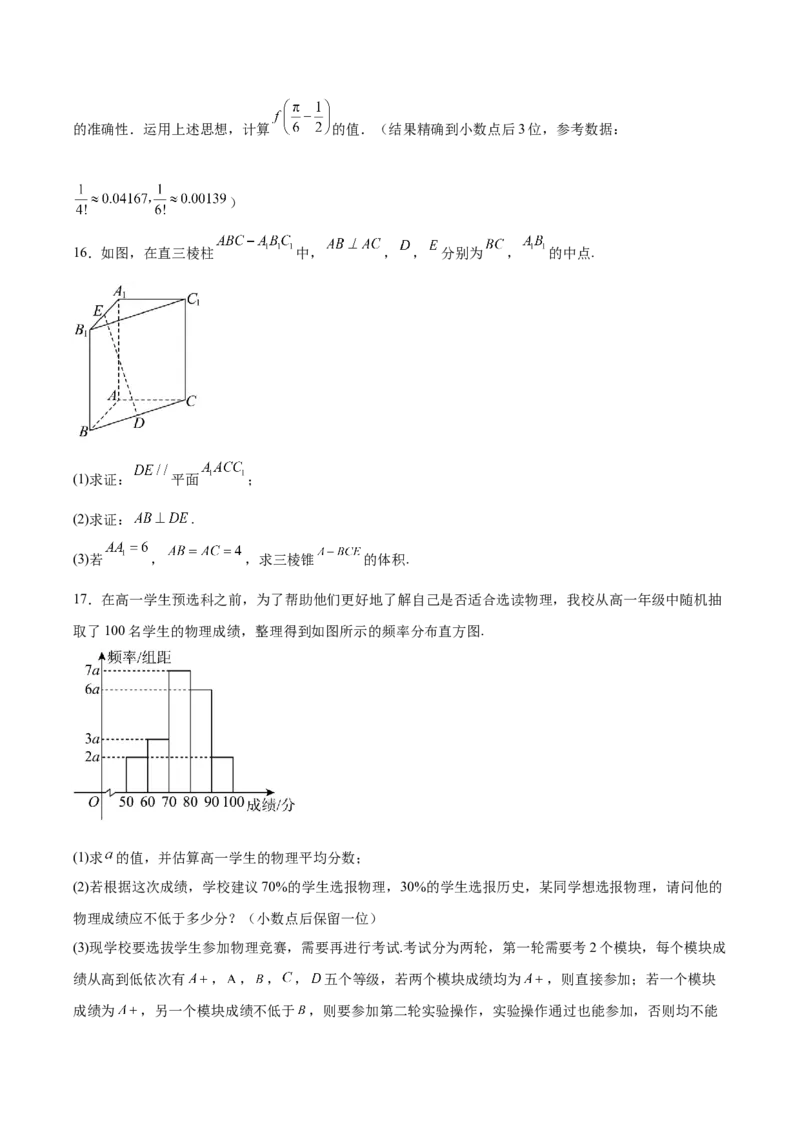
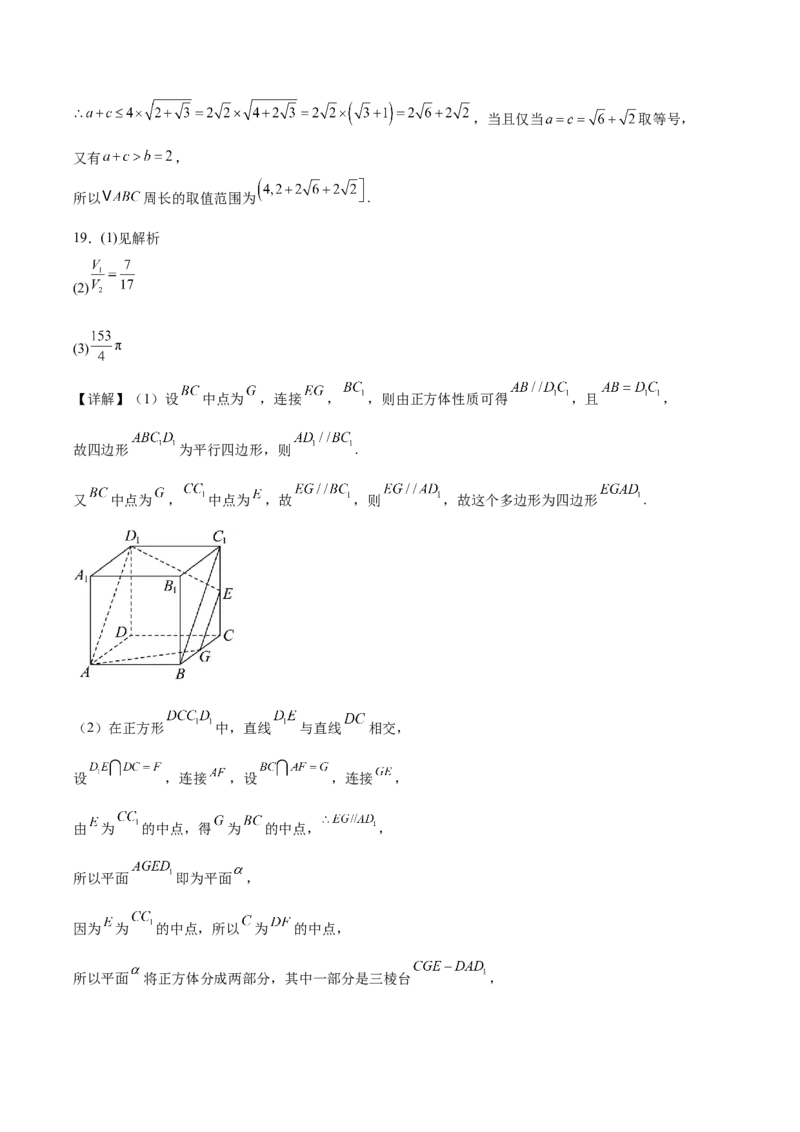
16.如图,在直三棱柱 中, , , 分别为 , 的中点.
(1)求证: 平面 ;
(2)求证: .
(3)若 , ,求三棱锥 的体积.
17.在高一学生预选科之前,为了帮助他们更好地了解自己是否适合选读物理,我校从高一年级中随机抽
取了100名学生的物理成绩,整理得到如图所示的频率分布直方图.
(1)求 的值,并估算高一学生的物理平均分数;
(2)若根据这次成绩,学校建议70%的学生选报物理,30%的学生选报历史,某同学想选报物理,请问他的
物理成绩应不低于多少分?(小数点后保留一位)
(3)现学校要选拔学生参加物理竞赛,需要再进行考试.考试分为两轮,第一轮需要考2个模块,每个模块成
绩从高到低依次有 , , , , 五个等级,若两个模块成绩均为 ,则直接参加;若一个模块
成绩为 ,另一个模块成绩不低于 ,则要参加第二轮实验操作,实验操作通过也能参加,否则均不能参加.现有甲、乙二人报名参加,二人互不影响,甲在每个模块考试中取得 , , , , 的概率分
别为 ;乙在每个模块考试中取得 , , , , 的概率分别为 ,甲、
乙在实验操作中通过的概率分别为 .求甲、乙能同时参加物理竞赛的概率.
18.在 中,内角 , , 所对的边分别为 , , , .
(1)求角 的值;
(2)若 的面积 ,且 ,求 ;
(3)若 ,求三角形 周长的取值范围.
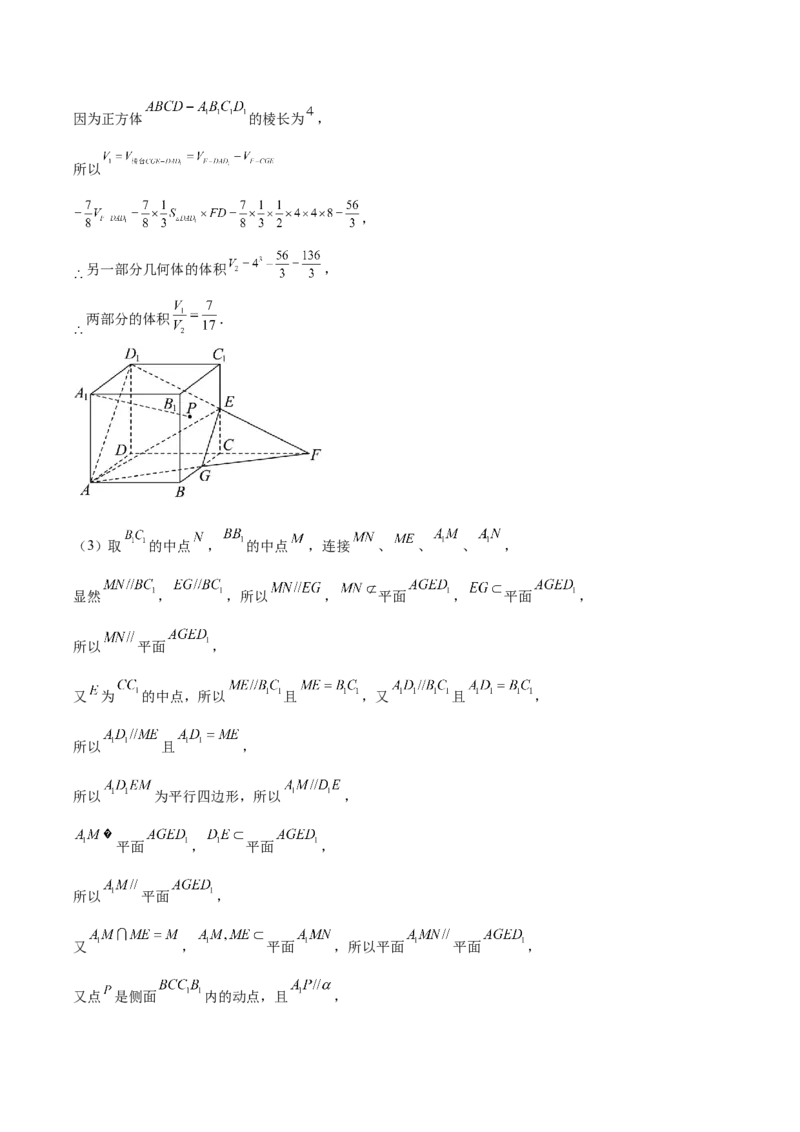
19.如图,在棱长为4的正方体 中, 为 的中点,过 , , 三点的平面 与此
正方体的面相交,交线围成一个多边形.
(1)在图中画出这个多边形(不必说出画法和理由);
(2)平面 将正方体 分成两部分,求这两部分的体积之比 (其中 );
(3)若点 是侧面 内的动点,且 ,当 最小时,求三棱锥 的外接球的表面积.
山东省德州市2024-2025学年高一下学期校际联考(四)(6月)数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C B C B C D ACD AD题号 11
答案 ACD
1.A
【详解】由 ,则 ,
所以 ,所以复数 的虚部为 .
故选:A.
2.D
【详解】由 ,又 ,且 , , 三点共线,
所以 ,则 .
故选:D
3.C
【详解】A:由 , ,根据面面平行的性质知 ,故A正确;
B:若 , , , ,
若 或 与 相交,则 相交或异面,显然与 矛盾,
故 都不与 相交,即 , ,此时有 ,故B正确;
C:若 , ,则 可能平行或异面,故C错误;
D:由 , ,根据线面垂直的性质知 ,故D正确.
故选:C.
4.B
【详解】由题设,两次向上的数字如下表(列表示第一次,行表示第二次),
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
所以抛掷两次的基本事件有36种,其中向上的数字之和是5的倍数的有7种,
分别为(1,4),(2,3),(3,2),(4,1),(5,5),(6,4),(4,6),
所以向上的数字之和是5的倍数的概率为 .
故选:B
5.C
【详解】由图知 ,可得 ,故 一组的频率为 ,A错;
由 , ,
所以众数为 ,B错;
由上 分位数位于 ,设为 ,则 ,
所以 ,C对;
由题设,80分以上的占比有 ,所以 人,D错.
故选:C
6.B
【详解】设 ,可得 , , ,
因为 是 的中点,所以 米,
由 ,得 ,
由 ,得 ,
所以 ,,解得 ,
所以该建筑的高度 米.
故选:B.
7.C
【详解】由 是偶函数,得 ,
展开整理得 ,所以 ,
又 , ,得 ,解得 ,
所以
,
当 时, 取得最大值 .
故选:C.
8.D
【详解】如图,连接 ,设 ,连接 ,则 平面 ,
取 的中点 ,连接 ,由正四棱锥的结构特征知 ,
所以 为侧面与底面所成的角,
设 ,则 ,在 中, ,所以 ,
又 ,所以 ,
所以正四棱锥 的每个侧面均为正三角形,
所以顶点 处的各面角分别为 、 、 ,该顶点处的曲率为 .
故选:D
9.ACD
【详解】 ,
对于A, ,故A正确;
对于B,复数 在复平面内对应的点 位于第四象限,故B错误;
对于C, ,故C正确;
对于D,由 ,得复数 在复平面内对应的点在以原点为圆心的单位圆上,
表示该圆上的点与点 的距离,其最小值为圆心到点 的距离减1,即 ,故D正确.
故选:ACD.
10.AD
【详解】对于A,甲队的极差为 ,乙队的极差为 , ,故A正确;
对于B,甲队得分平均数 ,
乙队得分平均数 , ,故B错误;
对于C,将甲队的数据由小到大排列: ,因为 ,所以甲队运动员得分的75%分位数
为12,故C错误;
对于D,由表中数据观察,乙队的得分更加集中,即相较于甲队,乙队运动员实力更均衡,故D正确.
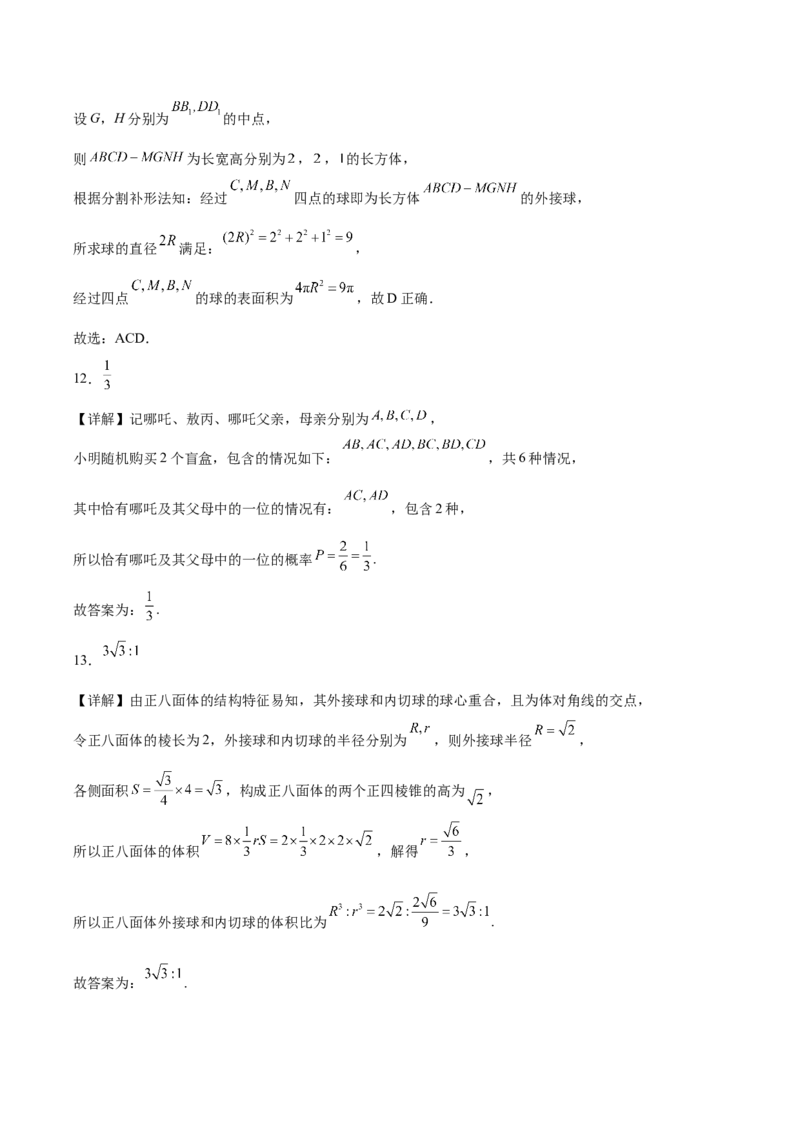
故选:AD.11.ACD
【详解】
连接 ,当 是 的中点时,
因为 ,所以 .
因为 平面 , 平面 ,所以 平面 ,故A正确,
如图,在正方体 中,连接 ,
因为 分别是 的中点,所以 ,
又因为 ,所以 ,所以 四点共面,
即当 与点 重合时, 四点共面,故B错误,
因为 为正方体,所以 平面 ,
直线 上的点到面 的距离为 ,而 ,
所以 是定值,故C正确,设G,H分别为 的中点,
则 为长宽高分别为 , , 的长方体,
根据分割补形法知:经过 四点的球即为长方体 的外接球,
所求球的直径 满足: ,
经过四点 的球的表面积为 ,故D正确.
故选:ACD.
12.
【详解】记哪吒、敖丙、哪吒父亲,母亲分别为 ,
小明随机购买2个盲盒,包含的情况如下: ,共6种情况,
其中恰有哪吒及其父母中的一位的情况有: ,包含2种,
所以恰有哪吒及其父母中的一位的概率 .
故答案为: .
13.
【详解】由正八面体的结构特征易知,其外接球和内切球的球心重合,且为体对角线的交点,
令正八面体的棱长为2,外接球和内切球的半径分别为 ,则外接球半径 ,
各侧面积 ,构成正八面体的两个正四棱锥的高为 ,
所以正八面体的体积 ,解得 ,
所以正八面体外接球和内切球的体积比为 .
故答案为: .14.
【详解】解:四面体 中 且异面直线 与 所成的角为
构建直三棱柱 ,设 分别为 的外心,连结 ,取其中点 ,
则 为直三棱柱 的外接球的球心,也是四面体ABCD的外接球的球心,
异面直线 与 所成角为 或 ,
设三棱柱底面 的外接圆半径为r,
则
当 ,
由余弦定理得: ,
,
,当且仅当 时等号成立,
四面体ABCD的体积:
当 ,
由余弦定理得: ,
,
,当且仅当 时等号成立,
即 ,当且仅当 时等号成立,四面体ABCD的体积:
综上可知四面体ABCD的体积的最大值为
故答案为:
15.(1) 或
(2)(i) ;(ii)
【详解】(1)若 ,则 ,
若 ,满足要求,此时 ,
若 ;
故 或 .
(2)(ⅰ) ,
令 ,
即 ,
所以函数 的单调递减区间 .
(ⅱ)因为 ,
所以 ,由泰勒公式得: ,
所以 .
16.(1)证明见解析;
(2)证明见解析;
(3) .
【详解】(1)取 的中点 ,连接 ,又 , 分别为 , 的中点,
所以 且 ,故四边形 为平行四边形,
所以 , 平面 , 平面 ,则 平面 ;
(2)取 中点 ,连 ,结合中位线及直棱锥的性质知 ,
由 且都在平面 内,则 平面 ,
由 平面 ,则 ;
(3)由 , , ,则 .
17.(1) , ;
(2) ;
(3) .
【详解】(1)依题意, ,所以 ;
物理平均分数 .
(2)由(1)知 , ,,
因此第 分位数位于 ,且 ,
所以他的物理成绩应不低于 分较为合适.
(3)依题意,甲能参加物理竞赛的概率 ,
乙能参加物理竞赛的概率 ,
所以甲、乙能同时参加物理竞赛的概率 .
18.(1)
(2)
(3)
【详解】(1)由 ,结合正弦定理得 ,
,化简整理得 ,
, ,得 ,故 .
(2)由 ,得 ,解得 ,
由余弦定理, ,
解得 .
(3)由余弦定理,可得 ,
, ,,当且仅当 取等号,
又有 ,
所以 周长的取值范围为 .
19.(1)见解析
(2)
(3)
【详解】(1)设 中点为 ,连接 , ,则由正方体性质可得 ,且 ,
故四边形 为平行四边形,则 .
又 中点为 , 中点为 ,故 ,则 ,故这个多边形为四边形 .
(2)在正方形 中,直线 与直线 相交,
设 ,连接 ,设 ,连接 ,
由 为 的中点,得 为 的中点, ,
所以平面 即为平面 ,
因为 为 的中点,所以 为 的中点,
所以平面 将正方体分成两部分,其中一部分是三棱台 ,因为正方体 的棱长为 ,
所以
,
另一部分几何体的体积 ,
两部分的体积 .
(3)取 的中点 , 的中点 ,连接 、 、 、 ,
显然 , ,所以 , 平面 , 平面 ,
所以 平面 ,
又 为 的中点,所以 且 ,又 且 ,
所以 且 ,
所以 为平行四边形,所以 ,
平面 , 平面 ,
所以 平面 ,
又 , 平面 ,所以平面 平面 ,
又点 是侧面 内的动点,且 ,所以 在线段 上,又 ,
即 为等腰三角形,所以当 为 的中点时 最小,
因为 为等腰直角三角形,所以其外接圆的圆心为斜边 的中点,设为 ,
令 ,则 为 的中点,连接 ,则 ,所以 平面 ,
所以球心在 上,设球心为 ,连接 、 、 ,
设外接球的半径为 , ,则 ,
又 , ,
所以 , ,解得 ,则 ,
所以外接球的表面积 .