文档内容
格致课堂
第七章 复数
一、单选题
1.已知复数 ,则 ( )
A. B. C. D.
【答案】B
【解析】
的实部为 ,虚部为 ,
故选
2. , 为虚数单位,若 ,则 的值为( )
A.1 B.-1 C.2 D.-2
【答案】A
【解析】由(m+i)(2﹣3i)=(2m+3)+(2﹣3m)i=5-i,
得 ,即m=1.
故选A.
( π π) ( π π)
3. cos +isin ×2 cos +isin =( )
6 6 3 3
A.2 B.-2 C.2 D.格致课堂
【答案】C
( π π) ( π π) (π π) (π π) π π
【解析】 cos +isin ×2 cos +isin =2cos + +2isin + =cos +isin =2i.
6 6 3 3 6 3 6 3 2 2
故选:C.
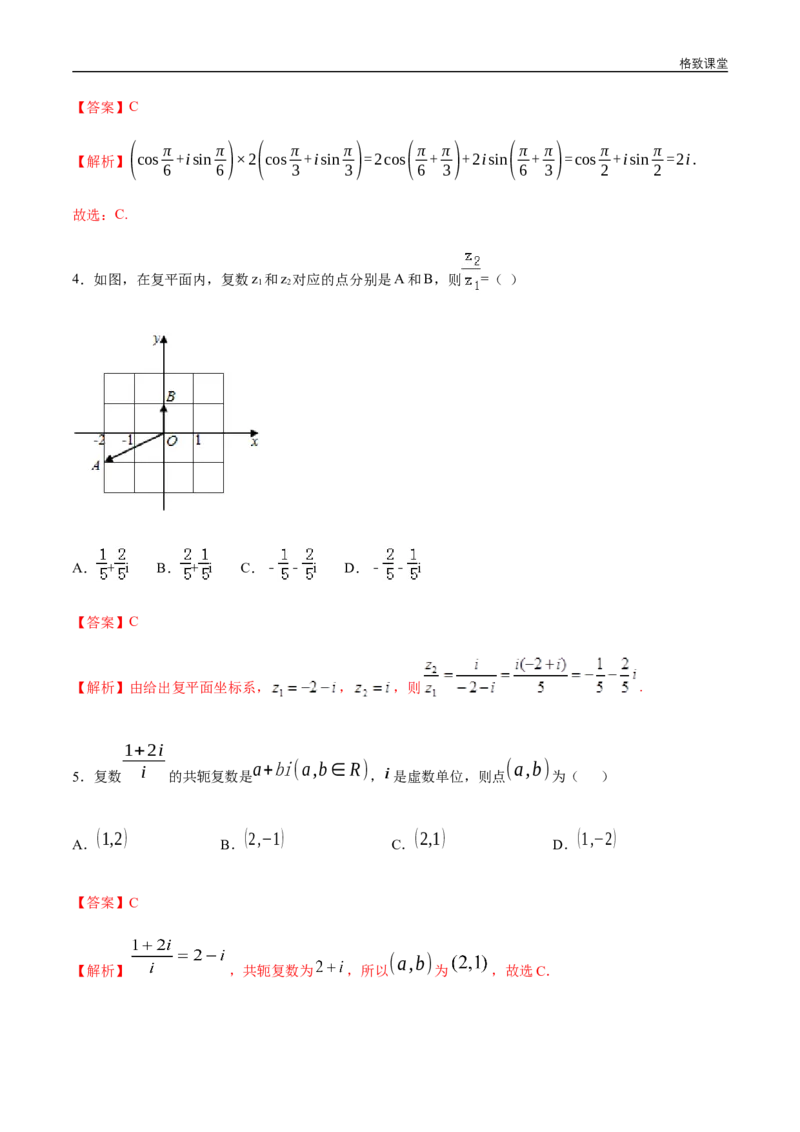
4.如图,在复平面内,复数z 和z 对应的点分别是A和B,则 =( )
1 2
A. + i B. + i C.﹣ ﹣ i D.﹣ ﹣ i
【答案】C
【解析】由给出复平面坐标系, , ,则 .
1+2i
5.复数 i 的共轭复数是
a+bi(a,b∈R)
,i是虛数单位,则点
(a,b)
为( )
(1,2) (2,−1) (2,1) (1,−2)
A. B. C. D.
【答案】C
(a,b)
【解析】 ,共轭复数为 ,所以 为 ,故选C.格致课堂
6.将复数(1,√3)对应的向量 绕原点按顺时针方向旋转 ,得到的向量为 ,那么 对应的复
数是( )
A. B. C. D.
【答案】A
【解析】复数 的三角形式是 ,向量 对应的复数是
故选:A
7.设a∈R,若 ( 为虚数单位)为正实数,则a=( )
A.2 B.1 C.0 D.-1
【答案】B
【解析】 ,因为 为正实数,所以 ,
(a-i) 2i=(a2-2ai+i2 )i=a2i-2ai2-i=2a+(a2-1)i 2a+(a2-1)i ¿
故选B
1+i
2015
( )
8.已知i是虚数单位,则 √2 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D格致课堂
【解析】由于 ,可知点位于第四象限,
故选D.
二、多选题
9.已知i为虚数单位,下列命题中正确的是( )
A.若 ,则 是纯虚数 B.虚部为 的虚数有无数个
C.实数集是复数集的真子集 D.两个复数相等的一个必要条件是它们的实部相等
【答案】BCD
【解析】对于A,若 ,则 ,不是纯虚数,故A错误;
对于B,虚部为 的虚数可以表示为 ,
有无数个,故B正确;
根据复数的分类,判断C正确;
两个复数相等一定能推出实部相等,必要性成立,
但两个复数的实部相等推不出两个复数相等,
充分性不成立,故D正确.
故选:BCD.
10.设复数z满足 ,i为虚数单位,则下列命题正确的是( )
A. B.复数z在复平面内对应的点在第四象限
C.z的共轭复数为 D.复数z在复平面内对应的点在直线 上格致课堂
【答案】AC
【解析】 ,A正确;复数z在复平面内对应的点的坐标为 ,在第三象限,B不
正确;z的共轭复数为 ,C正确;复数z在复平面内对应的点 不在直线 上,D不正确.
故选:AC
11.设 , , 为虚数单位,则以下结论正确的是( )
A. 对应的点在第一象限 B. 一定不为纯虚数
C. 一定不为实数 D.对应的点在实轴的下方
【答案】CD
【解析】 , ,
所以,复数 对应的点可能在第一象限,也可能在第二象限,故A错误;
当 ,即 或 时, 为纯虚数,故B错误;
因为 恒成立,所以 一定不为实数,故C正确;
由选项A的分析知, 对应的点在实轴的上方,所以 对应的点在实轴的下方,故D正确.
故选:CD.
12.已知i为虚数单位,下列说法中正确的是( )
A.若复数z满足 ,则复数z对应的点在以 为圆心, 为半径的圆上格致课堂
B.若复数z满足 ,则复数
C.复数的模实质上就是复平面内复数对应的点到原点的距离,也就是复数对应的向量的模
D.复数 对应的向量为 ,复数 对应的向量为 ,若 ,则
【答案】CD
【解析】满足 的复数z对应的点在以 为圆心, 为半径的圆上,A错误;
在B中,设 ,则 .
由 ,得 , 解得 ,B
错误;由复数的模的定义知C正确;
由 的几何意义知,以 , 为邻边的平行四边形为矩形,从而两邻边垂直,D正
确.
故选:CD
三、填空题
13.则复数 ,( 为虚数单位),则 的虚部等于 .
【答案】
【解析】因
=2−3i
.故应填答案 .
14.若复数 ( 为虚数单位),则 ______________.格致课堂
【答案】
【解析】为 ,所以 .因此 .
故答案为:
15.在复平面上,设点A、B、C ,对应的复数分别为 ,顺次过A、B、C 做平行四边形ABCD,
则点D的坐标为_______________.
(3,3)
【答案】 .
{x−4=−1¿¿¿¿
D(x,y) ⃗AB= ⃗DC −1−i=(x−4)+(2−y)i
【解析】设 ,由复数的几何意义,得 ,即 ,即 ,解
{x=3¿¿¿¿
得 ,即D的坐标为
(3,3)
.
16.若 , ,则 的最大值是______.
【答案】24
【解析】设 ,因为 ,所以 ,显然有
.
,
把 代入上式得: ,格致课堂
因为 ,所以当 时, 有最小值,最小值为 ;
当 时, 有最大值,最大值为24.
故答案为: 24
四、解答题
17.计算:
(1) ;
(2) .
【答案】(1) ;(2) .
【解析】(1)
(2)
18.已知复数z=(2+i)m2-3m(1+i)-2+2i.当实数m取什么值时,复数z是:
(1)实数;
(2)纯虚数;
(3)复平面内第二、四象限角平分线上的点对应的复数.
【答案】(1) m=1或m=2.格致课堂
1
(2)m=- .
2
(3)m=0或m=2.
【解析】z=2m2-3m-2+(m2-3m+2)i ,
(1)z为实数,则m2-3m+2=0,则m=1或m=2
2m2-3m-2=0 1
(2)z为纯虚数,则 { ,则m=- .
m2-3m+2≠0 2
(3)2m2-3m-2+(m2-3m+2)=0,则m=0或m=2.
19.已知复数 满足 .
(1)求复数 的共轭复数;
(2)若 ,且复数 对应向量的模不大于复数 所对应向量的模,求实数 的取值范围.
【答案】(1) (2)
【解析】⑴ ,所以复数 的共轭复数为
⑵ 复数 对应向量为
此时
又 复数 对应的向量
即 实数 的取值范围为格致课堂
20.已知复数 和 ,若 ,试求 的取
值范围.
【答案】 .
【解析】∵ ,∴ ,
∴ ,消去 得: ,
∴ ,
∵ ,∴当 时, .
当 时, .所以 的取值范围为: .
21.设 ,已知 , ,求 .
【答案】
【解析】(方法一)设 , ,
由题设知 , ,
.格致课堂
又由 ,
可得 .
∴ .∴ .
(方法二)∵ ,
将已知数值代入,可得 ,
∴ .
(方法三)作出 , 对应的向量 , ,
以 , 为邻边作平行四边形 ,如图所示.
∵ ,
又∵ , 不共线(若 , 共线,则 或0),
∴平行四边形 为菱形.
又∵ ,∴ ,格致课堂
∴平行四边形 为正方形,∴ .
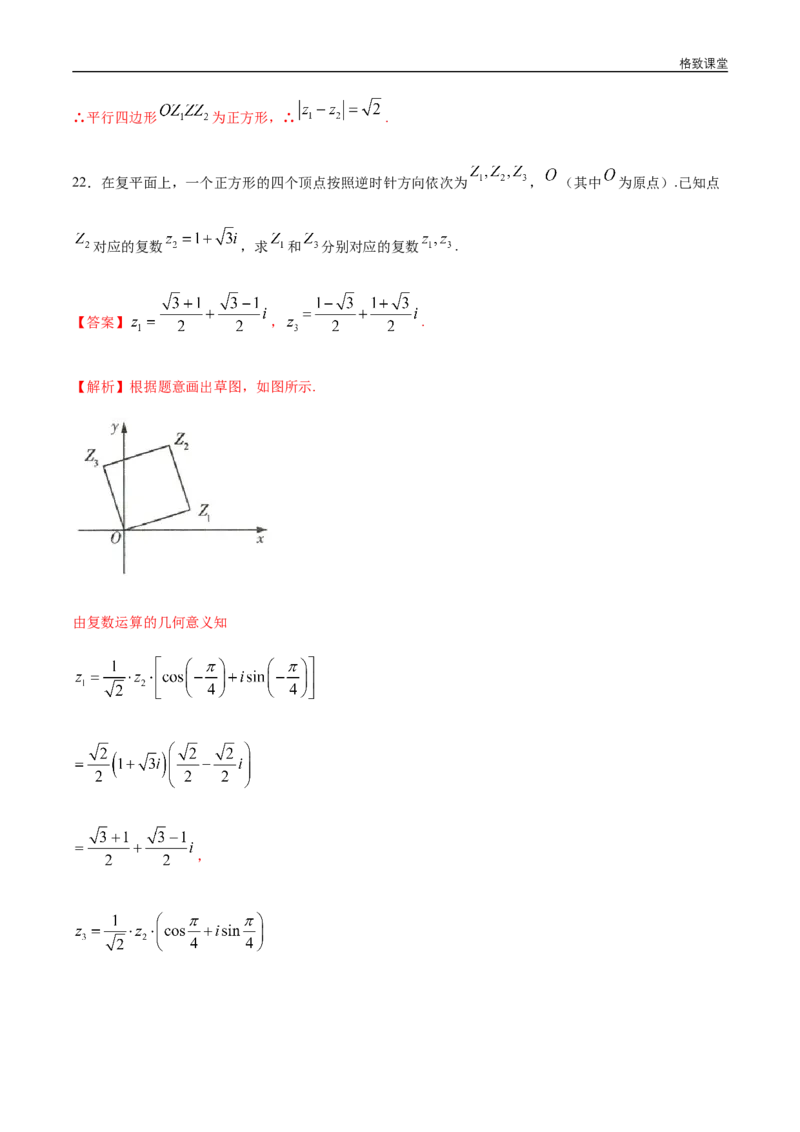
22.在复平面上,一个正方形的四个顶点按照逆时针方向依次为 , (其中 为原点).已知点
对应的复数 ,求 和 分别对应的复数 .
【答案】 , .
【解析】根据题意画出草图,如图所示.
由复数运算的几何意义知
,格致课堂
.